1. Introduction
In digital communication one of the important issues is how to transmit the message from the source to the destination as faithfully as possible. One of the most used techniques and also the most convenient is the adoption of error-correcting codes. Indeed the codes are used to improve the reliability of data transmitted over communication channels susceptible to noise. The Coding techniques are based on the following principle: Add the redundancy to the message to obtain a vector called “codeword”. Decoding techniques are based on the algorithms witch try to find the most likely transmitted code word related to the received (see Figure 1).
Decoding algorithms are classified into two categories: hard-decision and soft decision algorithms. Hard decision algorithms work on a binary form of the received information. In contrast, soft decision algorithms work directly on the received symbols [1].
Soft-decision decoding is an NP-hard problem and was approached in different ways. Recently artificial intelligence (AI) techniques were introduced to solve this problem. These techniques show very good results. Among related works, one work A* algorithm to decode linear block codes [2], another one uses genetic algorithms for decoding linear block codes [3] and a third one uses Compact Genetic Algorithms to decode BCH codes[4]. Maini et al. were the first, to our knowledge, to introduce Genetic algorithms [5] in the decoding of linear block codes. Hebbes et al. [6] worked on the integration of genetic algorithms in a classical turbo codes decoder, and Durand et al. [7] worked on the optimization of turbo decoding by optimizing the interleaver with a genetic algorithm. Furthermore the deployment of Artificial Neural Networks (ANN), to train the system for higher fault tolerance in OFDM is used by Praveenkumar [8]. There are also other works [9-11] based on AI trying to solve problems related to coding theory.
We have investigated the use of genetic algorithms in different ways. In [12], GA is used to search of good double-circulant codes. In [13], a new soft decoding of block codes based on the genetic algorithms with very good performances was presented.
The purpose of this paper is to complete the study of the decoder proposed in [14]. Indeed, at first we study the complexity of the decoder by comparing it with the complexity of the BMA and Chase decoders. Secondly, we apply it to the non-binary codes family such as Reed Solomon (RS) codes. And finally, we evaluate its performances on a Rayleigh fading channel.
The rest of this paper is organized as follows: Section 2 introduces the decoder based on genetic algorithms for linear block codes. The section 3 presents the Chase algorithms decoding and our soft decoding algorithm based on GA. In section 4 we study the complexity of the hard and the soft decoders. Simulation result are given in section 5, Section 6 concludes this paper.
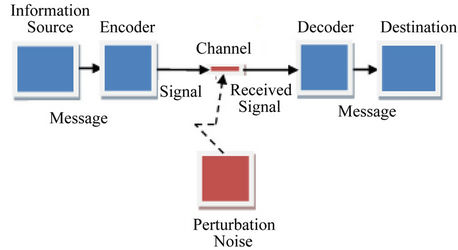
Figure 1. A simplified communication system model.
And before concluding this paper we present the experimentation results.
2. Hard-Decision Decoder Based on GA
2.1. Information Set (IS)
In a  linear block code, an information set is defined as set of k symbols of a codeword that can be independently specified. The remaining
linear block code, an information set is defined as set of k symbols of a codeword that can be independently specified. The remaining  elements are redundant parity-check symbols. Thus, if a received word has been corrupted by noise in some bits of the transmitted word, and if it is possible to find an error-free
elements are redundant parity-check symbols. Thus, if a received word has been corrupted by noise in some bits of the transmitted word, and if it is possible to find an error-free , so that all the wrong bits are paritycheck bits, then the received vector can be successfully decoded.
, so that all the wrong bits are paritycheck bits, then the received vector can be successfully decoded.
In this work, an  is represented by an n-dimensional vector in which k bits are equal to 1 and the others are set to 0. The non-zero bits of the
is represented by an n-dimensional vector in which k bits are equal to 1 and the others are set to 0. The non-zero bits of the  correspond to linearly independent columns of the matrix G such an information set is represented by the symbol p.
correspond to linearly independent columns of the matrix G such an information set is represented by the symbol p.
2.2. HDGA Algorithm
The purpose of the presented GA is to convert the decoding problem into search problem for a feasible solution around the received vector . In the presented case, the population will always consists of individuals which are intrinsically associated with codewords. Besides, the evolutionary operations over the individuals will always result in new individuals which are associated with codewords. The evolution, therefore, will take place within the constrained search space. After a finite number of generations, the best individual (codeword) in the population will become a highly evolved solution to the problem.
. In the presented case, the population will always consists of individuals which are intrinsically associated with codewords. Besides, the evolutionary operations over the individuals will always result in new individuals which are associated with codewords. The evolution, therefore, will take place within the constrained search space. After a finite number of generations, the best individual (codeword) in the population will become a highly evolved solution to the problem.
Step 1: Initial Population The initial population is obtained by random generation of N pairs of vectors  and
and  to form N individuals
to form N individuals .
.
Step 2: For i from 1 to 
Step 2.1: Crossover and replication The crossover operator provides 2N offspring as follows:
Choose form the intermediate population tow individuals at random, for example, ci = (r, pi) and ck = (r, pk).
Pair the  chromosome
chromosome  with
with  to generate a crossover
to generate a crossover  as described bellow.
as described bellow.
Set all n bits of  to zero.
to zero.
For each  do:
do:
If  do
do 
For each location of  that is equal to 1, get the corresponding columns of the generator matrix G to form a vectorial set. If this set is linearly dependent (LD), do:
that is equal to 1, get the corresponding columns of the generator matrix G to form a vectorial set. If this set is linearly dependent (LD), do:

End of for.
Since the code is , if only m positions were set to 1 in the IS chromosome, then the remaining
, if only m positions were set to 1 in the IS chromosome, then the remaining  positions equal to 0 must be used to find the remaining
positions equal to 0 must be used to find the remaining 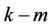 information bits. Thus, set at random
information bits. Thus, set at random  in the
in the  remaining zero bits, in such a way that
remaining zero bits, in such a way that  represents a valid information set of the code.
represents a valid information set of the code.
These offspring and parents are put together to from an intermediate population.
Step 2.2: Fitness evaluation The objective function is the Hamming distance between a codeword  and the received vector
and the received vector , given by
, given by . The fitness function can be simply defined as
. The fitness function can be simply defined as
 (1)
(1)
Step 2.3: Saving the Best Individuals The M fittest individuals are copied and saved.
Step 2.4: Mutation This operator alters an individual by bit inversion of chromosome X. However, such an inversion takes place only in one bit and only when an improvement in the individual’s fitness is achieved. If it is not possible to improve the individual‘s fitness, then no alteration is performed.
Step 2.5: Fitness evaluation Step 2.6: Saving the Best Individuals The M fittest individuals are copied and saved.
Step 2.7: Fitness evaluation Step 2.8: Selection The natural selection is used and the probability of selecting the ith individual of  the population, will be defined as
the population, will be defined as
 (2)
(2)
Step 2.9: Elitist strategy Restore the M best individuals.
Step 3: Solution The best member from the last generation is returned as the final decision.
3. Soft-Decision Decoding Based on Genetic Algorithm
3.1. Chase Algorithm
The Chase algorithm [15] is a suboptimal decoding procedure that uses a set of most likely error patterns. These error patterns are selected on the basis of the reliability of the received symbols. Each error pattern is added to the hard-decision received word and decoded using a harddecision decoder. Each decoded code word is scored by computing is metric with respect to the received sequence. The code word with the best metric is selected as the most likely.
3.2. SDGA Algorithm
Let C be a binary linear  block code where d is its minimum distance. C is capable to correct any combination of t or less random bit errors. Let
block code where d is its minimum distance. C is capable to correct any combination of t or less random bit errors. Let  be the received word from the output of the channel,
be the received word from the output of the channel, 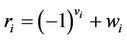 , where
, where  is a zeromean Gaussian random variable with variance
is a zeromean Gaussian random variable with variance ,
, .
.
The sign bits of the received values represent the harddecision
 ,
,

where

The reliabilities of the received channel values, for binary transmission over an  channel, are the amplitudes
channel, are the amplitudes . The received symbol reliabilities are ordered with a sorting algorithm (e.g., quick sort). The output of the algorithm is a list of indexes
. The received symbol reliabilities are ordered with a sorting algorithm (e.g., quick sort). The output of the algorithm is a list of indexes ,
,  such that
such that

In the first round of decoding, the hard-decision received word 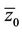 is fed into a HDGA. Let
is fed into a HDGA. Let  denote the decoded code word, stored as the initial code word guess. Then the metric of
denote the decoded code word, stored as the initial code word guess. Then the metric of 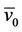 with respect to the received word
with respect to the received word
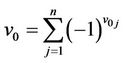 (4)
(4)
is computed and its value is stored as the maximum.
Test the error patterns with at most  errors located within the bit positions having the
errors located within the bit positions having the  lowest reliabilities.
lowest reliabilities.
• For , an error pattern
, an error pattern  is added to the hard-decision received word:
is added to the hard-decision received word: . The word “data” is plural, not singular.
. The word “data” is plural, not singular.
• The error patterns are generated among the t least reliable positions (LRPs), that is, Positions , for which reliabilities (amplitudes) are the smallest.
, for which reliabilities (amplitudes) are the smallest.
• Each test vector  is input to a HDGA, producing a codeword
is input to a HDGA, producing a codeword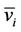 ,
, .
.
• The metric is computed according to Equation (3) and if maximum, code word  stored as the most likely.
stored as the most likely.
The Figure 2 below illustrates the steps of our SDGA algorithm.
4. Complexity Analysis
Let  be the code length,
be the code length,  be the code dimension,
be the code dimension,  be the error correction capability of a linear bloc code C,
be the error correction capability of a linear bloc code C,  be the population size which must be equal to the total number of individuals in the population, and let
be the population size which must be equal to the total number of individuals in the population, and let  be the number of generation. The Table 1 shows the complexity of the four algorithms.
be the number of generation. The Table 1 shows the complexity of the four algorithms.
For BMA, the complexity is polynomial in . Similarly, the complexity of HDGA is polynomial in
. Similarly, the complexity of HDGA is polynomial in ,
,  ,
,

Table 1. Complexity of BMA, HDGA, Chase-BMA, SDGA.
 ,
,  and
and . Although, the complexity of the Chase-BMA and SDGA is exponentially in
. Although, the complexity of the Chase-BMA and SDGA is exponentially in . For the non-binary codes, such as RS codes, all the expression in Table 1 must be multiplied by the term
. For the non-binary codes, such as RS codes, all the expression in Table 1 must be multiplied by the term .
.
We also note that BMA is less complex than HDGA. While the complexity of BMA is less than the decoder based on genetic algorithms, it can decode all linear codes while this is not the case for BMA and ChaseBMA.
5. Simulations Results
Computer simulations are carried out in order to evaluate the performance of the HDGA and SDGA decoding algorithm. Several RS and BCH codes are considered.
The simulations were made with the default parameters outlined in the Table 2 except where indicated. For transmission we used an AWGN/Rayleigh channel with a BPSK modulation.
5.1. HDGA versus BMA Performances
5.1.1. AWGN Channel
The Figures 3-5 below compare the performances of HDGA and BMA for the BCH(63,30,13), BCH(63,45,7) and the RS(15,7,9) codes.
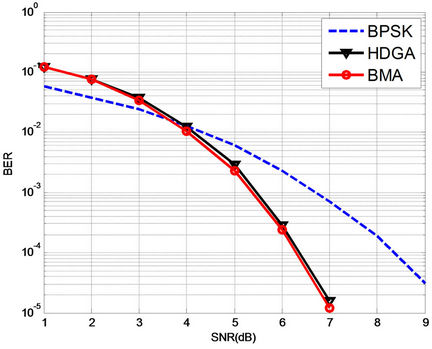
Figure 3. Performances of HDGA and BM algorithm for BCH(63,30,13).

Figure 4. Performances of HDGA and BM algorithm for BCH(63,45,7).

Figure 5. Performances of HDGA and BM algorithm for RS(15,7,9).
We notice in general the equality in terms of performance between the two decoders.
The performances of HDGA for RM(32,12,8) and Golay(23,12,7) codes, are shown in Figure 6. From the simulation results, we observe that the performances of the decoder HDGA realize about 2 dB coding gain from the non-coded BPSK curve. In addition the codes simulated in Figure 6 can’t be decoded by BMA.
5.1.2. Rayleigh Channel
HDGA has been described for the AWGN channel. The decoding is particularly desirable over channels with more severe impairments. Therefore a flat Rayleigh fading channel without side information is used for the performance investigation of HDGA.
The performances in terms of BER of HDGA and BMA for BCH(63,30,13) code are shown in Figure 7. From the later, we observe that the performances of both

Figure 6. Performances of HDGA for Golay(23,12,7) and RM(32,16,8).

Figure 7. Performances of HDGA and BMA for BCH(63,30, 13).
algorithms are similar.
Again, the Figure 8 shows that the two decoders present the same performances also for non-binary codes namely RS(15,7,9).
5.2. SDGA versus Chase-BMA Performance
In order to compare the SDGA with Chase-BMA and DDGA [13] algorithms, we carried out some simulations using transmission over AWGN channel and then over Rayleigh channel.
5.2.1. AWGN Channel
The Figures 9 and 10 compare the performance of the three decoders namely SDGA, Chase-BM and DDGA applied on the BCH(63,45,7) and RS(15,7,9) codes. We show that the performances of DDGA are better than both SDGA and Chase-BM algorithms which present relatively the same performances. This is can be explain by the fact that DDGA explore about 30,000 test vectors,

Figure 8. Performances of HDGA and BMA for RS(15,7,9).

Figure 9. Performances of SDGA and Chase-BMA for BCH (63,45,7).
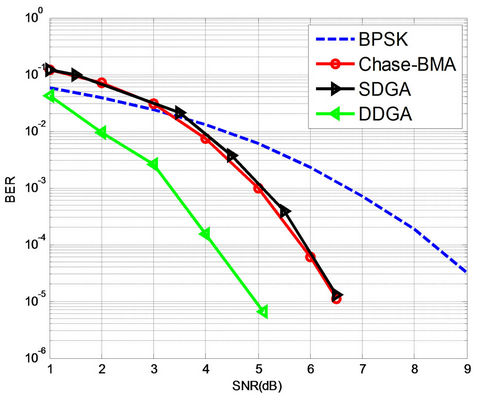
Figure 10. Performances of SDGA and Chase-BMA for RS(15,7,9).
whoever, the other decoders operate respectively 8 and 16 test vectors for BCH(63,45,7) and RS(15,7,9) codes.
The performances of SDGA for RM(32,12,8) and Golay(23,12,7) codes, are shown in Figure 11. From the very figure, we observe that the performance of our algorithm gives an important coding gain. Furthermore, in our algorithm, the algebraic decoding is not required as is the case of the Chase algorithm.
5.2.2. Rayleigh Channel
To evaluate more our soft decoding algorithm, we process some simulations in the Rayleigh channel, and we compare them with the performances of Chase-BMA using respectively BCH and RS(15,7,5) codes. The curves plotted in Figures 12 and 13 shows that the performance of our soft decoding algorithm SDGA are comparables with those of Chase-BMA one. So we have in the case of Rayleigh fading channel the same behavior as in the case

Figure 11. Performances of HDGA for Golay(23,12,7) and RM(32,16,8).

Figure 12. Performances of HDGA and BMA for BCH(63, 30,13).

Figure 13. Performances of HDGA and BM algorithm for RS(15,7,9).
of AWGN channel.
6. Conclusions
In this paper, we have presented a hard and soft decoders based on GA. These decoders can be applied on binary and non-binary linear block codes; and constitute in fact evolutionary versions of the well known “information set decoding”. Their computational complexity is also studied and compared with BMA and Chase-BMA.
The simulations are curried out for some binary and non-binary Linear Block Codes over Gaussian and Rayleigh channels. They show that our SDGA decoder presents the same performances as Chase-BMA. In addition our SDGA decoder does not require algebraic decoding as is the case of the Chase-BM algorithm. The obtained results will open new horizons for the artificial intelligence algorithms in the coding theory field.