Integral Means of Univalent Solution for Fractional Differential Equation ()
1. Introduction
Recently, the theory of fractional calculus has found interesting applications in the theory of analytic functions. The classical definitions of fractional operators and their generalizations have fruitfully been applied in obtaining, for example, the characterization properties, coefficient estimates [1], distortion inequalities [2] and convolution structures for various subclasses of analytic functions and the works in the research monographs. In [3], Srivastava and Owa, gave definitions for fractional operators (derivative and integral) in the complex z-plane 
as follows:
Definition 1.1. The fractional derivative of order 
is defined, for a function 
by
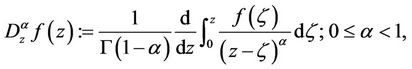
where the function 
is analytic in simply-connected region of the complex z-plane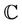 
containing the origin and the multiplicity of 
is removed by requiring 
to be real when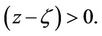 
Definition 1.2. The fractional integral of order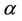 
is defined, for a function
, by
where the function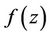 
is analytic in simply-connected region of the complex z-plane (
) containing the origin and the multiplicity of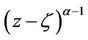 
is removed by requiring 
to be real when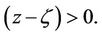 
Remark 1.1.
and
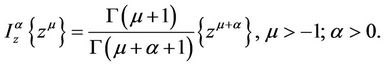
Further properties of these operators can be found in [4,5].
2. Preliminaries
Let 
be the class of all normalized analytic functions 
in the open unit disk 
satisfying 
and 
Let 
be the class of analytic functions in U and for any 
and 
be the subclass of 
consisting of functions of the form 
For given two functions F and G, which are analytic in U, the function F is said to be subordinate to G in U if there exists a function h analytic in U with
such that
We denote this subordination by
. If G is univalent in U, then the subordination 
is equivalent to 
and 
Lemma 2.1 [6]. If the functions f and g are analytic in U then
Lemma 2.2 [7]. Let f, g be analytic function in U. Assume that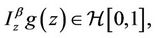 
and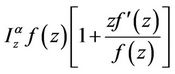 
is univalent in U. If
then 
Our work is organized as follows: In Section 2, we will derive the integral means for normalized analytic functions involving fractional integral in the open unit disk U
In Section 3, we study the existence of locally univalent solution for the fractional diffeo-integral equation
(1)
subject to the initial condition 
where 
is an analytic function for all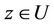 
and 
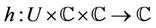are analytic univalent functions in
. The existence is shown by using Schauder fixed point theorem while the uniqueness is verified by using Banach fixed point theorem.
For that purpose we need the following definitions and results:
Let M be a subset of Banach space X and 
an operator. The operator A is called compact on the set M if it carries every bounded subset of M into a compact set. If A is continuous on M (that is, it maps bounded sets into bounded sets) then it is said to be completely continuous on M. A mapping 
is said to be a contraction if there exists a real number 
such that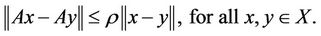 
Theorem 2.1. Arzela-Ascoli let E be a compact metric space and 
be the Banach space of real or complex valued continuous functions normed by
If 
is a sequence in 
such that 
is uniformly bounded and equi-continuous, then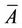 
is compact.
Theorem 2.2. (Schauder) Let X be a Banach space,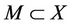 
a nonempty closed bounded convex subset and 
is compact. Then P has a fixed point.
Theorem 2.3. (Banach) If X is a Banach space and 
is a contraction mapping then P has a unique fixed point.
3. Existence and Uniqueness
In this section, we established the existence and uniqueness solution for the diffeo-integral Equation (1). Let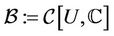 
be a Banach space of all continuous functions on U endowed with the sup. norm 
Lemma 3.1. If the function h is analytic, then the initial value problem (1) is equivalent to the nonlinear Volterra integral equation
(2)
In other words, every solution of the Volterra Equation (2) is also a solution of the initial value problem (1) and vice versa.
The following assumptions are needed in the next theorem:
(H1) There exists a continuous function 
on U and increasing positive function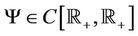 
such that
with the property that
Note that 
is the Banach space of all continuous positive functions.
(H2) There exists a continuous function p in U, such that
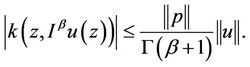
Remark 3.1. By using fractional calculus we observe that Equation (2) is equivalent to the integral equation of the form
(3)
that is, the existence of Equation (2) is the existence of the Equation (3).
Theorem 3.1. Let the assumptions (H1) and (H2) hold. Then Equation (1) has a univalent solution 
on U.
Proof. We need only to show that 
has a fixed point by using Theorem 1.2 where
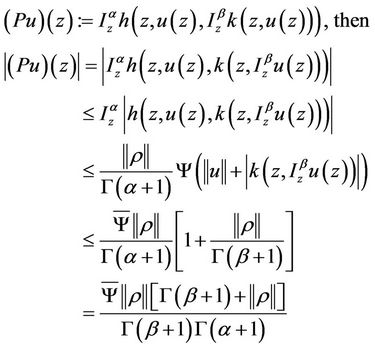(4)
where 
Thus we obtain that
that is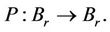 
Then P mapped 
into itself. Now we proceed to prove that P is equicontinuous. For 
such that 
,
. Then for all 
where
we obtained
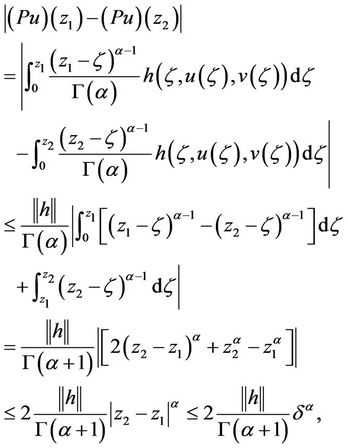
which is independent of u.
Hence P is an equicontinuous mapping on S. Moreover, for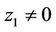
, 
such that 
and under assumption (H1), we show that P is a univalent function. The Arzela-Ascoli theorem yields that every sequence of functions 
from 
has a uniformly convergent subsequence, and therefore 
is relatively compact. Schauder’s fixed point theorem asserts that P has a fixed point. The univalency of the function h yields that u is a univalent solution.
Now we discuss the uniqueness solution for the problem (1). For this purpose let us state the following assumptions:
(H3) Assume that there exists a positive number L such that for each
, 
and 
(H4) Assume that there exists a positive number 
such that for each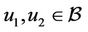 
we have
Theorem 3.2. Let the hypotheses (H1-H4) be satisfied. If 
then (1) admits a unique univalent solution 
Proof. Assume the operator P defined in Equation (4), we only need to show that P is a contraction mapping that is P has a unique fixed point which is corresponding to the unique solution of the Equation (1). Let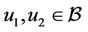
, then for all 
we obtain that
Thus by the assumption of the theorem we have that P is a contraction mapping. Then in view of Banach fixed point theorem, P has a unique fixed point which corresponds to the univalent solution (Theorem 3.1) of Equation (1). Hence the proof.
The next result shows the integral means of univalent solutions of problem (1).
Theorem 3.3. Let
, 
be two analytic univalent solutions for the Equation (1) satisfying the assumptions of Lemma 2.2 with 
and 
then
Proof. Setting
, 
, Lemma 2.2 implies that
. Hence in view of Lemma 1.2, we obtain the result.
Example 3.1. Consider the fractional problem
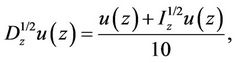(5)
where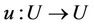 
and 
We observe that 
and 
and
where 
and 
Thus in view of Theorem 3.1, the problem (5) has a solution in the unit disk.