Aiming at Delaunay triangulation with islets constrains in terrain simulation. A general Delaunay triangulation algorithm for constrained data set with islets is proposed. The algorithm firstly constructs Constrained Delaunay Triangulation with constraint polygons which are inner boundary of islets, then according to topological relations within edge, surface, arc segment, applies bidirectional search to find the triangle in islet, lastly it carries on certain corresponding processing to complete the Delaunay triangulation algorithm with islets. The analyses show the algorithm simple, fast speed. The algorithm can be used in 3-D terrain vision.
1. Introduction
The triangulation has a wide range of applications in the GIS, geology, computer graphics, virtual reality and so on. Delaunay triangulation has the most performance in the terrain simulation. The build Delaunay triangulation technology taking into account the mandatory constraint data in the establishment of high-quality DEM played a decisive role [1]. At present, based on the points, line segments constrained, the Delaunay triangulation (CDT) has been a lot of algorithms. But the triangulation with the islets constrained data field, due to the complex of data constraint, it is necessary to satisfy the constraints and the characteristics of Delaunay triangulation, so the algorithm with great difficulty [2,3]. The existing triangulation algorithm needs to determine the convex-concave of nature polygon, or using connect bridge technology, the algorithms or more complex, or the result is not Delaunay triangulation [4-8]. This paper proposes an algorithm solution to the islets constrained, the algorithms is simple, without determine the convex-concave of polygon and geometric intersection Computing.
2. With Islets Constrained Triangulation Algorithm
2.1. The Basic Concept of the Islets
Anyone of islet can be abstracted into polygon (convexconcave polygon). The line of Constituted polygonal called arc, polygon composed by arc is Islet, polygon does not contain islet called a simple polygon, is single-connected region, the polygon with islet called compound polygon, is complex connected region. In the complex connected region, including the outer boundary and inner boundaries, the islet polygon is inner boundary. The Polygons with islets was defined as follows: Set P1, P2, ..., Pn (n > 1) are simple polygon, if the degrees of all vertex of Pi (i = 1,2, ..., n) is 2, the edges without common vertex do not intersect, and one of polygons (set Pj, 1 ≤ j ≤ n) included all the other polygons, then the polygon composed by P1, P2, ..., Pn is called islet polygons (shown in Figure 1), P1 is called the outer polygon, the other is called the inner polygon (islet or hole) [7].
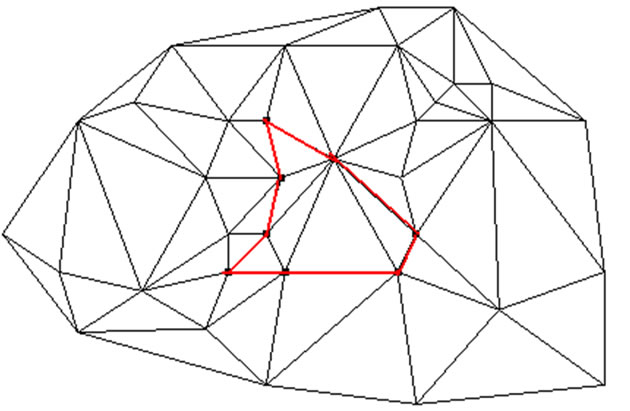
Figure 1. Constrained triangulation segment.
Triangulation with islets constraints is build delaunary triangulation between the islets and outer boundary that is with islets.
2.2. Classic Triangulation Algorithm with Islets Constraints
For the Delaunay triangulation algorithm with islets constrained, according to occasion of islets constrained data embedded, can be divided into the following categories:
1) Taking into account the impact of islets In the Delaunay triangulation, directly build Delaunay Triangulation with islets constraint. Such as the Triangulation algorithm with islets constrained data fields proposed by Liu Shao-Hua [4].
2) First, without considering islets constraints, building Delaunay triangulation with all the vertex of islet polygons and edges constraints, then delete the triangles within constraints fields. Such as Reference [7,8]. These algorithms are simple, compatible with non-constrained Delaunay triangulation.
3. Improvement of Delaunary Triangulation with Islets Constraints
3.1. Algorithm Theory
Two-dimensional Delaunay triangulation with islets constrained is described as: For the plane field D (P, Q), it containing a set of points P and Q, Q = {Qi ∈ D|I = 1, n2} is a points set that distributed in the boundary of islets, if a triangulation of the point set P, Q is a Delaunay triangulation (DT), delete the triangle within the islets, then it is a Delaunay triangulation with islets constrained on the plane field D (P, Q) [8].
Based on the above principle, we can build Delaunay triangulation with islets constrained step by step. First, without considering the nature of boundary points of islets, building Delaunay triangulation with the P and Q, then embedding edge constraint, the edges constrained are boundary line segment of islets, shown in Figure 1. Finally we found all the triangles inside the islets, according to need to be deleted, or retained. Based on the relationship between edges and triangles, this paper proposed a bi-directional search method and found all the triangles inside island, in order to complete with island constraints DT division.
3.2. Data Structure
According to the algorithm needs to establish topological relations among point, line, surface, and arc. This data structure can preferably establish topology data model of triangular mesh, and can be quickly index at the point, edge, triangle, and arcs. The algorithm is program with the Java, The data structure is as follows:
1) The point class:
public class Point{//class Point public double x, y, z;
}
2) The edge class:
In order to finding two triangles that hane one and the same edge quickly, so the class has the two neighbor triangles.
Public class Edge {//Edge private int [] pointNum = new int[2]
//the point number private Triangle [] tri = new Triangle[2];
//Edges corresponding to two adjacent triangles private boolean constrainEdge = false;
//is it binding edge
}
3) The triangle class:
In order to finding the edge of the triangle quickly, so the class has the three edges.
Public class Triangle {//class Triangle private int [] pointNum = new int [3];
//Triangle of three dots private Edge [] edge = new Edge [3];
//Side of the object created by the three Edge
}
4) The islet class:
Storages a list of all inner border line segment of islet, according to counter-clockwise storages.
Public class IsletArea {//Islet Class private List
Pointlist = new LinkedList
();
//the Island of arc
}
5) The Islets influence field class:
The internal class, record the edge within islet, and a known triangle in a side of the edge a.
private class IsletDomain {
private Edge e; //Islands within the affected side of private Triangle tri; //Islandsthathey affect a certain edge e adjacent to a known triangle
}
Considering the deleted or retained the triangle within Islands, in the algorithm, there is a list that stores the triangular within islet.
3.3. Algorithm Implementation
Assume all the arcs that surround the inner border of islets are counter-clockwise order, so the left side of closed arcs is within the islets, the right is exterior the islet, the triangle on the left of the arcs fall within the islet. The key of algorithm is to find the triangle within the islet, based on the relationship between the edges and the triangle, from a known triangle and a triangle edge start to expend the other two edges of the known triangle and the adjacent triangle both sides, until the find all the triangles within the islets, the steps are as follows:
1) Doing Delaunay triangulation for the islets boundary points and the other discrete points within the plane.
2) All the borders of the islets are as line segment constraints, embedded in the Delaunay triangulation, carried out Delaunay triangulation with constraints, stored line segment constraints into constraint edge list.
3) Order all line segment constraints in the constraint edge list by counter-clockwise.
4) Pick-up any inner boundary arc (edge) e from anyone islets, and two triangles both sides e, to find the left side triangle t from these two triangles, building a new IsletDomain object with e and t, push it into the stack. Modify the topology of e, set the reference (pointer) of e and t to null.
5) Pick-up the top element of the stack, that is a IsletDomain object. Store the member triangle of IslandDomain, tri, into triangle within islets list, and pick-up the other two side edges of the tri, from the two direction to search, there are three situation:
•Two edges are not in the constraint edge list;
•one edge is the constraint edge list, another edge is not in the constraint edge list;
•Two edges are in the constraint edge list.
For three cases, if the edge is in the constraint edge list, looking for adjacent triangle of the edge, building the IsletDomain object, push stack; if the edge is not in the constraint edge list, modify the topology of the edge, set the reference (pointer) of the triangle that pointed to by tri to null.
6) Redo step 5, until the stack is empty.
7) According to the needs, delete or retain elete the triangles in the triangle within islets list.
Based on the above steps, the flow chart of Delaunay triangulation with island constraint is Figure 2.
Based on the above steps to complete Delaunay triangulation with islets constrained, the result shown in Figure 3.
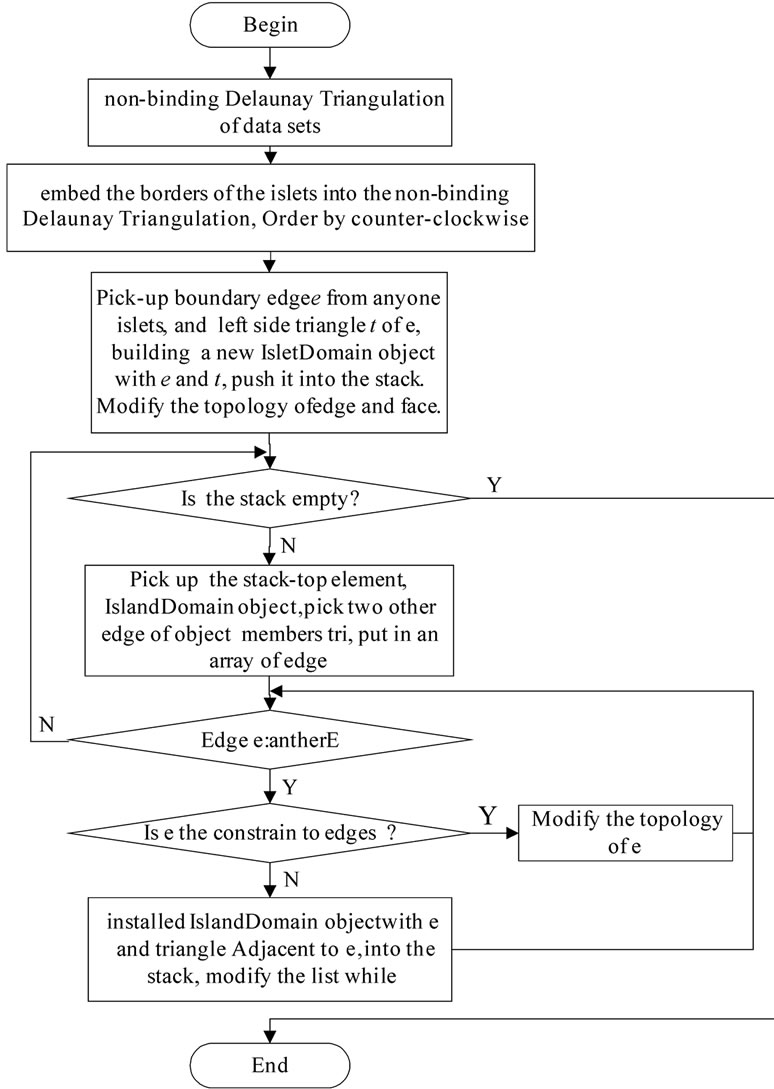
figure 2. flow diagram of delaunay triangulation with islets constrained.

Figure 3. Delaunay triangulation with an islet constrained.
4. Algorithms Analysis
Tang Wei proposed algorithm and Ma Hong-bin proposed algorithm, simple, do not to determine the convexconcave of polygon and geometric intersection operations. Tang Wei’s algorithm to find a triangle within islets by the line segment constraints that enclosed the islets, therefore, for the complex islets, there may be do not find all triangles within islet. (a) and (b) of Figure 4 is
 (a)
(a) (b)
(b)
Figure 4. Tang Wei’s algorithm effect diagram. (a) Triangular mesh based on lines list; (b) Triangular form based on triangular mesh.

Table 1. Algorithms comparison.
based on the line list and triangles list the algorithm generated to form a Triangular mesh. Through the figure can know that the algorithm can remove the extra line in the line list, but can not remove the redundant triangles in the triangle list.
For the algorithm of Ma Hong-bin, asked the three vertices of all triangles in the triangulation are the vertex of the polygon, that is restrictive conditions, is not suitable for large scattered set of points and more Islets.
The algorithm of Center of gravity location triangle counts needs to determine all the triangles whether in the polygon, and the need for geometric intersection operations. When the triangular mash is more large, and a lot of Islets, it will waste too much resources when determination if the triangle is not within islets. Compared with algorithm proposed in this paper, the data shown in Figure 5, the results of comparison is table 1.
5. Conclusions
Through the studied and summarized for existing algorithms, according to the topological relations between edges and triangles, proposed a method of looking for triangles within the islets, the algorithm simple, without geometric intersection operations. The algorithms been used in 3-D terrain model.
[1] Z. M. Ma and B. Luo, “Entire Optimized Triangulation Algorithm of Delaunay Triangle Network for DEM Construction,” Journal of Chang’an University (Natural Science Edition), Vol. 28, No. 3, 2008, pp. 44-48.
[2] L. P. Chew, “Constrained Delaunay Triangulations,” ACM Symposium on Computational Geometry, Springer-Verlag, Berlin, 1987, pp. 215-222.
[3] L. X. Wu, Y. B. Wang and W. Z. Shi, “Integral Ear Elimination and Virtual Point Based Updating Algorithms for Constraint Delaunay TIN,” Science in China: E, Vol. 51, No. S1, 2008, pp. 135-144.
[4] S. H. Liu, P. G. Cheng and H. H. Chen, “Study of Algorithm for Triangulation of Restrained Data Set with Islets,” Computer Application, Vol. 23, No. 4, 2003, pp. 96-98.
[5] S. G. Deng, M. Chen, et al., “Study on Algorithm for Delaunay Triangular Irregular Network of Islets Constrained Data Field,” Science of Surveying and Mapping, Vol. 32, No. 5, 2007, pp. 63-64.
[6] M. Lamot and B. Zalik, “A Fast Polygon Triangulation Algrithm Based on Uniform Plane Subdivision,” Computers and Graphics, Vol. 27, No. 2, 2003, pp. 239-253.
[7] H. B. Ma, J. T. Guo, et al., “Study on Delaunay Triangulation Algorithm for Polygon with inside Islets,” Journal of Northeastern University (Natural Science), Vol. 30, No. 5, 2009, pp. 733-736.
[8] W. Tang, S. Z. Chen, et al., “An Approach to the Modification of the Triangulation Algorithm with Islets Constrains,” Hydrogeology & Engineering Geology, Vol. 33, No. 5, 2006, pp. 58-60.