Intelligent Optimization Methods for High-Dimensional Data Classification for Support Vector Machines ()
Support vector machine (SVM) is a popular pattern classification method with many application areas. SVM shows its outstanding performance in high-dimensional data classification. In the process of classification, SVM kernel parameter setting during the SVM training procedure, along with the feature selection significantly influences the classification accuracy. This paper proposes two novel intelligent optimization methods, which simultaneously determines the parameter values while discovering a subset of features to increase SVM classification accuracy. The study focuses on two evolutionary computing approaches to optimize the parameters of SVM: particle swarm optimization (PSO) and genetic algorithm (GA). And we combine above the two intelligent optimization methods with SVM to choose appropriate subset features and SVM parameters, which are termed GA-FSSVM (Genetic Algorithm-Feature Selection Support Vector Machines) and PSO-FSSVM (Particle Swarm Optimization-Feature Selection Support Vector Machines) models. Experimental results demonstrate that the classification accuracy by our proposed methods outperforms traditional grid search approach and many other approaches. Moreover, the result indicates that PSO-FSSVM can obtain higher classification accuracy than GA-FSSVM classification for hyperspectral data.
1. Introduction
Support vector machine (SVM) was first proposed by Vapnik [1] and has recently been applied in a range of problems including pattern recognition, bioinformatics and text categorization. SVM classifies data with different class labels by determining a set of support vectors that are members of the set of training inputs that outline a hyperplane in the feature space. When using SVM, two issues should be solved: how to choose the optimal input feature subset for SVM, and how to set the best kernel parameters. Traditionally, the two issues are solved separately ignoring their close connections, this always leads low classification accuracy. These two problems are crucial, because the feature subset choice influences the appropriate kernel parameters and vice versa [2]. Therefore, obtaining the optimal feature subset and SVM parameters must occur simultaneously.
Feature selection is used to identify a powerfully predictive subset of fields within a database and reduce the number of fields presented to the mining process. By extracting as much information as possible from a given data set while using the smallest number of features, we can save significant computational time and build models that generalize better for unseen data points. Feature subset selection is an important issue in building an SVM-based classification model.
As well as feature selection, the proper setting of parameters for the SVM classifier can also increase classification accuracy. The parameters that should be optimized include penalty parameter C and the kernel function parameters such as the gamma (γ) for the radial basis function (RBF) kernel. To design a SVM classifier, one must choose a kernel function, set the kernel parameters and determine a soft margin constant C (penalty parameter). As a rule, the Grid algorithm is an alternative to finding the best C and gamma (γ) when using the RBF kernel function. However, this method is time consuming and does not perform well [3]. Moreover, the Grid algorithm can not perform the feature selection task.
Both feature subset selection and model parameter setting substantially influence classification accuracy. The optimal feature subset and model parameters must be determined simultaneously. Since feature subset and model parameters greatly affects the classification accuracy.
To simultaneously optimize the feature subset and the SVM kernel parameters, this study attempts to increase the classification accuracy rate by employing two evolutionary computing optimization-based approaches: genetic algorithm (GA) and particle swarm optimization (PSO) in SVM. These novel approaches are termed PSO-FSSVM (Particle Swarm Optimization-Feature Selection Support Vector Machines) and GA-FSSVM (Genetic Algorithm-Feature Selection Support Vector Machines). The developed approaches not only tune the parameter values of SVM, but also identify a subset of features for specific problems, maximizing the classification accuracy rate of SVM. This makes the optimal separating hyperplane obtainable in both linear and non-linear classification problems.
The remainder of this paper is organized as follows. Section 2 reviews pertinent literature on SVM and the feature selection. Section 3 then describes basic GA concept and GA-FSSVM model of feature selection and parameter optimization. Also, Section 3 then describes in detail the developed PSO-FSSVM approach for determining the parameter values for SVM with feature selection. Section 4 compares the experimental results with those of existing traditional approaches. Conclusions are finally drawn in Section 5, along with recommendations for future research.
2. Literature Review
Approaches for feature selection can be categorized into two models, namely a filter model and a wrapper model [4]. Statistical techniques, such as principal component analysis, factor analysis, independent component analysis and discriminate analysis can be adopted in filterbased feature selection approaches to investigate other indirect performance measures, most of which are based on distance and information. Chen and Hsieh [5] presented latent semantic analysis and web page feature selection, which are combined with the SVM technique to extract features. Gold [6] presented a Bayesian viewpoint of SVM classifiers to tune hyper-parameter values in order to determine useful criteria for pruning irrelevant features.
The wrapper model [7] applies the classifier accuracy rate as the performance measure. Some researchers have concluded that if the purpose of the model is to minimize the classifier error rate, and the measurement cost for all the features is equal, then the classifier’s predictive accuracy is the most important factor. Restated, the classifier should be constructed to achieve the highest classification accuracy. The features adopted by the classifier are then chosen as the optimal features. In the wrapper model, meta-heuristic approaches are commonly employed to help in looking for the best feature subset. Although meta-heuristic approaches are slow, they obtain the (near) best feature subset. Shon [8] employed GA to screen the features of a dataset. The selected subset of features is then fed into the SVM for classification testing. Zhang [9] developed a GA-based approach to discover a beneficial subset of features for SVM in machine condition monitoring. Samanta [10] proposed a GA approach to modify the RBF width parameter of SVM with feature selection. Nevertheless, since these approaches only consider the RBF width parameter for the SVM, they may miss the optimal parameter setting. Huang and Wang [11] presented a GA-based feature selection and parameters optimization for SVM. Moreover, Huang et al. [12] utilized the GA-based feature selection and parameter optimization for credit scoring.
Several kernel functions help the SVM obtain the optimal solution. The most frequently used such kernel functions are the polynomial, sigmoid and radial basis kernel function (RBF). The RBF is generally applied most frequently, because it can classify high-dimensional data, unlike a linear kernel function. Additionally, the RBF has fewer parameters to set than a polynomial kernel. RBF and other kernel functions have similar overall performance. Consequently, RBF is an effective option for kernel function. Therefore, this study applies an RBF kernel function in the SVM to obtain optimal solution. Two major RBF parameters applied in SVM, C and γ, must be set appropriately. Parameter C represents the cost of the penalty. The choice of value for C influences on the classification outcome. If C is too large, then the classification accuracy rate is very high in the training phase, but very low in the testing phase. If C is too small, then the classification accuracy rate is unsatisfactory, making the model useless. Parameter γ has a much greater influence on classification outcomes than C, because its value affects the partitioning outcome in the feature space. An excessively large value for parameter γ results in over-fitting, while a disproportionately small value leads to under-fitting. Grid search [13] is the most common method to determine appropriate values for C and γ. Values for parameters C and γ that lead to the highest classification accuracy rate in this interval can be found by setting appropriate values for the upper and lower bounds (the search interval) and the jumping interval in the search. Nevertheless, this approach is a local search method, and vulnerable to local optima. Additionally, setting the search interval is a problem. Too large a search interval wastes computational resource, while too small a search interval might render a satisfactory outcome impossible.
In addition to the commonly used grid search approach, other techniques are employed in SVM to improve the possibility of a correct choice of parameter values. Pai and Hong [14] proposed an SA-based approach to obtain parameter values for SVM, and applied it in real data; however, this approach does not address feature selection, and therefore may exclude the optimal result. As well as the two parameters C and γ, other factors, such as the quality of the feature’s dataset, may influence the classification accuracy rate. For instance, the correlations between features influence the classification result. Accidental removal of important features might lower the classification accuracy rate. Additionally, some dataset features may have no influence at all, or may contain a high level of noise. Removing such features can improve the searching speed and accuracy rate.
It is worth underlining that the kernel-based implementation of SVM involves the problem of the selection of multiple parameters, including the kernel parameters (e.g., the γ and p parameters for the Gaussian and polynomial kernels, respectively) and the regularization parameters C.
Studies have also illustrated that a radial basis kernel yields the best results in remote sensing applications [15, 16]. We chose to use the radial basis kernel for SVM in this study. The verification of the applicability of other specialized kernel functions for the classification of remote sensing data may be used in future studies. The equation for the radial basis kernel is
 (1)
(1)
where γ represents a parameter inversely proportional to the width of the Gaussian kernel.
3. The Proposed GA-FSSVM and PSO-FSSVM Models
3.1. Genetic Algorithm
The genetic algorithms are inspired by theory of evolution; it is type of an evolutionary computing. The problems are solved by an evolutionary process resulting in a fittest solution in genetic algorithm. A genetic algorithm (GA) is used to solve global optimization problems. The procedure starts from a set of randomly created or selected possible solutions, referred to as the population. Every individual in the population means a possible solution, referred to as a chromosome. Within every generation, a fitness function should be used to evaluate the quality of every chromosome to determine the probability of it surviving to the next generation; usually, the chromosomes with larger fitness have a higher survival probability. Thus, GA should select the chromosomes with larger fitness for reproduction by using operations like selection, crossover and mutation in order to form a new group of chromosomes which are more likely to reach the goal. This reproduction goes through one generation to another, until it converges on the individual generation with the most fitness for goal functions or the required number of generations was reached. The optimal solution is then determined.
GA coding strategies mainly include two sectors: one sector recommends the least digits for coding usage, such as binary codes, another one recommends using the real-valued coding based on calculation convenience and accuracy. Binary codes are adopted for the decision variables in solving the discrete problems, a suitable encoding scheme is needed to encode the chromosome of each individual, in our study, an encoding scheme is usually a binary string. We may define the length of bit string according the precision.
3.2. GA-FSSVM Model
As mentioned before, a kernel function is required in SVM for transforming the training data. This study adopts RBF as the kernel function to establish support vector classifiers, since the classification performance is significant when the knowledge concerning the data set is lacking. Therefore, there are two parameters, C and γ, required within the SVM algorithm for accurate settings, since they are closely related to the learning and predicting performance. However, determining the values exactly is difficult for SVM. Generally, to find the best C and γ, a given parameter is first fixed, and then within the value ranges another parameter is changed and cross comparison is made using the grid search algorithm. This method is conducted with a series of selections and comparisons, and it will face the problems of lower efficiency and inferior accuracy when conducting a wider search. However, GA for reproduction could provide the solution for this study. The scheme of an integration of GA and SVM is shown in Figure 1, to establish a training and SVM classification model that can be used to determine optimized SVM parameters and subset features mask. Following the above scheme of the proposed GA-FSSVM model, Figure 1 describes the operating procedure in this study.
A fitness function assesses the quality of a solution in the evaluation step. The crossover and mutation functions are the main operators that randomly impact the fitness value. Chromosomes are selected for reproduction by evaluating the fitness value. The fitter chromosomes have higher probability to be selected into the recombination pool using the roulette wheel or the tournament selection methods. New population replaces the old population using the elitism or diversity replacement strategy and forms a new population in the next generation. The evolutionary process operates many generations until termination condition is satisfied.
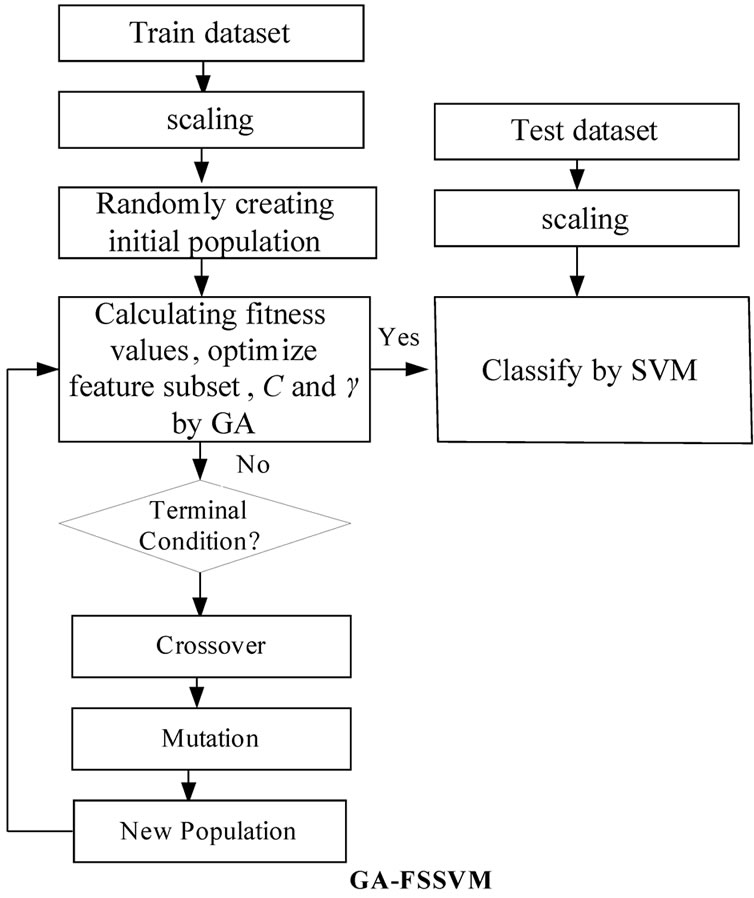
Figure 1. system architecture of the integrated GA-FSSVM scheme.
To implement our proposed approach, this research uses the RBF kernel function for the SVM classifier because the RBF kernel function can analysis higher-dimensional data and requires that only two parameters, C and γ be defined When the RBF kernel is selected, the parameters (C and γ) and features used as input attributes must be optimized using our proposed GA-based system. Therefore, the chromosome comprises three parts: C, γ and the features mask. However, these chromosomes have different parameters when other types of kernel functions are selected. The binary coding system is used to represent the chromosome.
Figure 2 shows the binary chromosome representation of our design. In Figure 2, 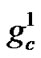 ~
~ represents the value of parameter C,
represents the value of parameter C, 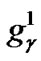 ~
~ represents the parameter value γ, and
represents the parameter value γ, and  ~
~ represents the feature mask.
represents the feature mask.  is the number of bits representing parameter C,
is the number of bits representing parameter C, 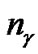 is the number of bits representing parameter g, and
is the number of bits representing parameter g, and 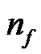 is the number of bits representing the features. Note that we can choose
is the number of bits representing the features. Note that we can choose 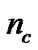 and
and  according to the calculation precision required, and that
according to the calculation precision required, and that 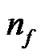 equals the number of features varying from the different datasets. In Figure 2, the bit strings representing the genotype of parameter C and γ should be transformed into phenotype. Note that the precision of representing parameter depends on the
equals the number of features varying from the different datasets. In Figure 2, the bit strings representing the genotype of parameter C and γ should be transformed into phenotype. Note that the precision of representing parameter depends on the