
on the maximum modulus of  on
on  for arbitrary real or complex numbers
for arbitrary real or complex numbers ,
,  with
with ,
,  and
and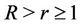 , and present certain sharp operator preserving inequa-lities between polynomials.
, and present certain sharp operator preserving inequa-lities between polynomials.
1. Introduction to the Statement of Results
Let  denote the space of all complex polynomials
denote the space of all complex polynomials  of degree n. If
of degree n. If , then concerning the estimate of the maximum of
, then concerning the estimate of the maximum of  on the unit circle
on the unit circle  and the estimate of the maximum of
and the estimate of the maximum of  on a larger circle
on a larger circle , we have
, we have
 (1)
(1)
and
 (2)
(2)
Inequality (1) is an immediate consequence of S. Bernstein’s theorem (see [1-3]) on the derivative of a trigonometric polynomial. Inequality (2) is a simple deduction from the maximum modulus principle (see [4, p. 346] or [5, p. 158]). If we restrict ourselves to the class of polynomials  having no zero in
having no zero in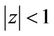 , then (1) and (2) can be replaced by
, then (1) and (2) can be replaced by
 (3)
(3)
and
 (4)
(4)
Inequality (3) was conjectured by Erdös and later verified by Lax [6]. Ankeny and Rivlin [7] used Inequality (3) to prove Inequality (4).
As a compact generalization of Inequalities (1) and (2), Aziz and Rather [8] have shown that if , then for every real or complex number
, then for every real or complex number 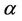 with
with ,
,  and
and ,
,
 (5)
(5)
The result is sharp.
As a corresponding compact generalization of Inequalities (3) and (4), they [8] have also shown that if , and
, and  for
for , then for every real or complex number
, then for every real or complex number  with
with ,
, 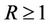 ,
,
 (6)
(6)
for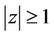 . The result is sharp and equality in (6) holds for
. The result is sharp and equality in (6) holds for ,
, .
.
Consider an operator B which carries a polynomial  into
into
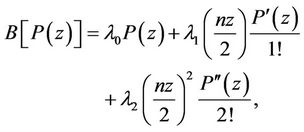 (7)
(7)
where ,
,  and
and  are such that all the zeros of
are such that all the zeros of
 (8)
(8)
lie in the half plane
 (9)
(9)
As a generalization of the Inequalities (1) and (2), Q.I. Rahman [9] proved that if , then for
, then for ,
,
 (10)
(10)
and if  for
for , then for
, then for ,
,
 (11)
(11)
(see [9], Inequality (5.2) and (5.3)).
In this paper, we consider a problem of investigating the dependence of

on the maximum modulus of  on
on  for arbitrary real or complex numbers
for arbitrary real or complex numbers ,
,  with
with ,
,  and
and , and develop a unified method for arriving at these results. In this direction we first present the following interesting result which is compact generalization of the Inequalities (1), (2), (5) and (10).
, and develop a unified method for arriving at these results. In this direction we first present the following interesting result which is compact generalization of the Inequalities (1), (2), (5) and (10).
Theorem 1. If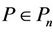 , then for arbitrary real or complex numbers
, then for arbitrary real or complex numbers  and
and  with
with ,
, 
 and
and ,
,
 (12)
(12)
where

The result is best possible and equality in (12) holds for 
Remark 1. For  from Inequality (12), we have for
from Inequality (12), we have for ,
,  ,
,  and
and 
 (13)
(13)
Remark 2. For  and
and , Inequality (12) reduces to
, Inequality (12) reduces to
 (14)
(14)
for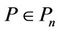 ,
,  and
and , which contains Inequality (10) as a special case.
, which contains Inequality (10) as a special case.
Remark 3. For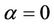 , Inequality (12) yields,
, Inequality (12) yields,
 (15)
(15)
for  and
and .
.
If we choose  in (12) and noting that all the zeros of
in (12) and noting that all the zeros of  defined by (8) lie in the half plane (9), we get:
defined by (8) lie in the half plane (9), we get:
Corollary 1. If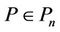 , then for all real or complex numbers
, then for all real or complex numbers  and
and  with
with ,
,  ,
,  and
and ,
,
 (16)
(16)
where  is defined as in Theorem 1. The result is sharp and equality in (16) holds for
is defined as in Theorem 1. The result is sharp and equality in (16) holds for ,
, 
For the case , from (12) we obatin for all real or complex numbers
, from (12) we obatin for all real or complex numbers  and
and  with
with ,
,  ,
,  and
and ,
,
 (17)
(17)
Inequality (17) is equivalent to the Inequality (5) for  and
and . For
. For  and
and , Inequality (17) includes Inequality (2) as a special case.
, Inequality (17) includes Inequality (2) as a special case.
Next we use Theorem 1 to prove the following result.
Theorem 2. If , then for arbitrary real or complex numbers
, then for arbitrary real or complex numbers  and
and  with
with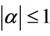 ,
,  ,
,  and
and ,
,
 (18)
(18)
where  and
and  is defined as in Theorem 1.
is defined as in Theorem 1.
The result is sharp and equality in (18) holds for ,
, 
Remark 4. Theorem 2 includes some well known polynomial inequalities as special cases. For example, inequality (18) reduces to a result due to Q. I. Rahman ([8], Inequality (5.2) with  and
and ). Also for
). Also for , Inequality (18) gives
, Inequality (18) gives
 (19)
(19)
for ,
,  and
and .
.
If we take  in (18), we get:
in (18), we get:
Corollary 2. If , then for all real or complex numbers
, then for all real or complex numbers  and
and  with
with ,
,  ,
,  and
and ,
,
 (20)
(20)
where 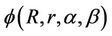 is defined as in Theorem 1. The result is sharp and equality in (20) holds for
is defined as in Theorem 1. The result is sharp and equality in (20) holds for ,
, 
For  and
and ,
,  , Theorem 2 includes a result due to A. Aziz and Rather [2] as a special case.
, Theorem 2 includes a result due to A. Aziz and Rather [2] as a special case.
Inequality (12) can be sharpened if we restrict ourselves to the class of polynomials  having no zeros in
having no zeros in . In this direction we next prove the following result which is a compact generalization of the Inequalities (3), (4) and (6).
. In this direction we next prove the following result which is a compact generalization of the Inequalities (3), (4) and (6).
Theorem 3. If  and
and  for
for , then for arbitrary real or complex numbers
, then for arbitrary real or complex numbers  and
and  with
with ,
,  ,
,  and
and ,
,
 (21)
(21)
where  is defined as in Theorem 1. The result is sharp and equality in (21) holds for
is defined as in Theorem 1. The result is sharp and equality in (21) holds for 
Remark 5. Inequality (11) is a special case of the Inequality (21) for  and
and . If we choose
. If we choose 
 in (21) and note that all the zeros of
in (21) and note that all the zeros of  defined by (8) lie in the half plane defined by (9), it follows that if
defined by (8) lie in the half plane defined by (9), it follows that if  and
and  for
for , then for
, then for ,
,  and
and ,
,  ,
,
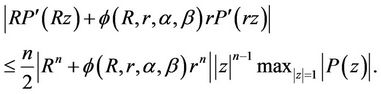 (22)
(22)
Setting  in (22), we obtain for
in (22), we obtain for ,
,
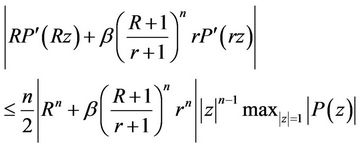 (23)
(23)
for ,
,  and
and .
.
Taking  in (22), we obtain for
in (22), we obtain for ,
,  and
and ,
,
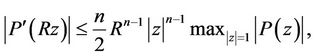 (24)
(24)
which in particular gives Inequality (3).
Next choosing  in (21), we immediately get for
in (21), we immediately get for ,
,  and
and ,
,  ,
,
 (25)
(25)
which is a compact generalization of the Inequalities (3), (4) and (6). The result is sharp and equality in (25) holds for ,
, 
If we put  in (25), we get the following result.
in (25), we get the following result.
Corollary 3. If , and
, and  for
for , then for every real or complex number
, then for every real or complex number  with
with ,
,  and
and ,
,
 (26)
(26)
A polynomial  is said to be self-inversive if
is said to be self-inversive if
 where
where . It is known [610] that if
. It is known [610] that if  is a self-inversive polynomial, then
is a self-inversive polynomial, then
 (27)
(27)
Here finally, we establish the following result for self-inversive polynomials Theorem 4. If  is a self-inversive polynomial, then for arbitrary real or complex numbers
is a self-inversive polynomial, then for arbitrary real or complex numbers  and
and 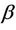 with
with ,
, 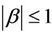 ,
,  and
and ,
,
 (28)
(28)
where 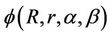 is defined as in Theorem 1. The result is sharp and equality in (21) holds for
is defined as in Theorem 1. The result is sharp and equality in (21) holds for 
The following result is an immediate consequence of Theorem 4.
Corollary 4. If  is a self-inversive polynomial, then for arbitrary real or complex numbers
is a self-inversive polynomial, then for arbitrary real or complex numbers  and
and 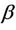 with
with ,
,  ,
,  and
and ,
,
 (29)
(29)
where  is defined as in Theorem 1. The result is best possible For
is defined as in Theorem 1. The result is best possible For  the Inequality (29) reduces to
the Inequality (29) reduces to
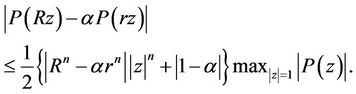 (30)
(30)
Remark 6. Inequality (6) is a special case of the Inequality (30). Many other interesting results can be deduced from Theorem 4 in the same way as we have deduced from Theorem 1 and Theorem.
2. Lemmas
For the proofs of these theorems, we need the following lemmas. The first lemma can be easily proved.
Lemma 1. If  and
and  has all its zeros in
has all its zeros in , then for every
, then for every  and
and ,
,
 (31)
(31)
The next Lemma follows from corollary 18.3 of [11, p. 65].
Lemma 2. If  and
and  has all its zeros in
has all its zeros in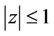 , then all the zeros of
, then all the zeros of  also lie in
also lie in .
.
Lemma 3. If  and
and  does not vanish in
does not vanish in , then for arbitrary real or complex numbers
, then for arbitrary real or complex numbers  and
and  with
with ,
,  ,
, 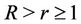 and
and ,
,
 (32)
(32)
where and
and  is defined as in Theorem 1.
is defined as in Theorem 1.
The result is sharp and equality in (32) holds for 
Proof of Lemma 3. Since the polynomial  has all its zeros in
has all its zeros in  for every real or complex number
for every real or complex number  with
with , the polynomial
, the polynomial where
where , has all its zeros in
, has all its zeros in 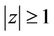 with atleast one zero in
with atleast one zero in , so that we can write
, so that we can write

where  and
and 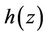 is a polynomial of degree
is a polynomial of degree  having all its zeros in
having all its zeros in .
.
Applying lemma 1 to the polynomial , we obtain for
, we obtain for  and
and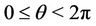 ,
,

This implies for 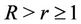 and
and ,
,
 (33)
(33)
Since  so that
so that  for
for  and
and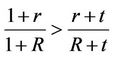 , from Inequality (33), we obtain for
, from Inequality (33), we obtain for  and
and ,
,
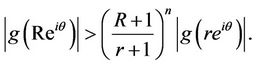 (34)
(34)
Equivalently,

for  and
and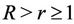 . Hence for every real or complex number
. Hence for every real or complex number  with
with  and
and  we have
we have
 (35)
(35)
for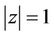 . Also, Inequality (34) can be written as
. Also, Inequality (34) can be written as
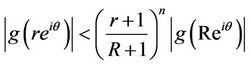 (36)
(36)
for every  and
and  Since
Since  and
and , from inequality (36), we obtain for
, from inequality (36), we obtain for  and
and ,
,

Equivalently,

Since all the zeros of 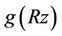 lie in
lie in , a direct application of Rouche’s theorem shows that the polynomial
, a direct application of Rouche’s theorem shows that the polynomial  has all its zeros in
has all its zeros in  for every real or complex number
for every real or complex number  with
with . Applying Rouche’s theorem again, it follows from (35) that for arbitrary real or complex numbers
. Applying Rouche’s theorem again, it follows from (35) that for arbitrary real or complex numbers  with
with ,
,  and
and , all the zeros of the polynomial
, all the zeros of the polynomial

lie in  with
with . Applying Lemma 2 to the polynomial
. Applying Lemma 2 to the polynomial 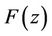 and noting that B is a linear operator, it follows that all the zeros of the polynomial
and noting that B is a linear operator, it follows that all the zeros of the polynomial

lie in  for all real or complex numbers
for all real or complex numbers  with
with ,
,  ,
,  and
and . This implies
. This implies
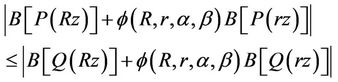 (37)
(37)
for ,
,  ,
,  and
and . If Inequality (38) is not true, then there is a point
. If Inequality (38) is not true, then there is a point  with
with  such that
such that

But all the zeros of 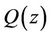 lie in
lie in , therefore, it follows (as in case of
, therefore, it follows (as in case of ) that all the zeros of
) that all the zeros of

lie in . Hence by Lemma 2, all the zeros of
. Hence by Lemma 2, all the zeros of

lie in , so that
, so that

We take

then  is a well defined real or complex number with
is a well defined real or complex number with 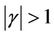 and with this choice of
and with this choice of , from (37) we obtain
, from (37) we obtain 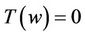 where
where . This contradicts the fact that all the zeros of
. This contradicts the fact that all the zeros of  lie in
lie in . Thus
. Thus

for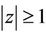 ,
,  ,
,  and
and . This proves (38) and hence Lemma 3.
. This proves (38) and hence Lemma 3.
3. Proofs of the Theorems
Proof of Theorem 1. Let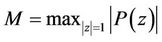 , then
, then
 for
for . By Rouche’s Theorem, it follows that all the zeros of the polynomial
. By Rouche’s Theorem, it follows that all the zeros of the polynomial  lie in
lie in  for every real or complex number
for every real or complex number  with
with , therefore, as before (as in Lemma 3), we conclude that all the zeros of the polynomial
, therefore, as before (as in Lemma 3), we conclude that all the zeros of the polynomial

lie in  for all real or complex numbers
for all real or complex numbers  and
and 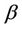 with
with  and
and . Hence by Lemma 2, the polynomial
. Hence by Lemma 2, the polynomial

has all its zeros in 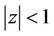 for every real or complex number
for every real or complex number  with
with . This implies for every real or complex numbers
. This implies for every real or complex numbers  and
and  with
with ,
,  and
and ,
,
 (38)
(38)
If Inequality (40) is not true, then there is a point  with
with  such that
such that

Since , we take
, we take

so that  is a well defined real or complex number with
is a well defined real or complex number with  and with this choice of
and with this choice of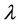 , from (39) we get
, from (39) we get 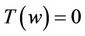 where
where . This contradicts the fact that all the zeros of
. This contradicts the fact that all the zeros of  lie in
lie in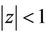 . Thus for every real or complex numbers
. Thus for every real or complex numbers  and
and  with
with ,
, 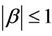 and
and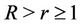 ,
,

This completes the proof of Theorem 1.
Proof of Theorem 2. Let , then
, then
 for
for . If
. If  is any real or complex number with
is any real or complex number with , then by Rouche’s Theorem, the polynomial
, then by Rouche’s Theorem, the polynomial  does not vanish in
does not vanish in . Applying Lemma 3 to the polynomial
. Applying Lemma 3 to the polynomial  and using the fact that B is a linear operator, it follows that for all real or complex numbers
and using the fact that B is a linear operator, it follows that for all real or complex numbers  and
and 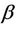 with
with ,
,  ,
,  and for
and for 

where

 Using the fact that
Using the fact that , we obtain
, we obtain

for all real or complex numbers  and
and  with
with ,
,  ,
,  and
and . Now choosing the argument of
. Now choosing the argument of  such that
such that

which is possible by Theorem 1, we get

for ,
,  ,
,  and
and . This implies
. This implies

for ,
,  ,
,  and
and . Letting
. Letting , we obtain
, we obtain

which is inequality (18) and this proves Theorem 2.
Proof of Theorem 3. Lemma 3 and Theorem 2 together yields for all real or complex numbers  and
and  with
with ,
,  ,
,  and
and ,
,

which gives

which is the Inequality (21) and this completes the proof of Theorem 3.
Proof of Theorem 4. Since  is a self-inversive polynomial of degree n, therefore
is a self-inversive polynomial of degree n, therefore

for all . This implies, in particular, that for all real or complex numbers
. This implies, in particular, that for all real or complex numbers 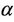 and
and  with
with ,
,  ,
, 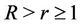 and
and ,
,

Combining this with Theorem 2, the desired result follows immediately. This completes the proof of Theorem 4.
4. Acknowledgements
Authors are thankful to the referee for his suggestions.