The Efficiency of Reduced Beam Section Connections for Reducing Residual Drifts in Moment Resisting Frames ()
1. Introduction
In recent years, the downside of permanent displacements in moment resisting frames (MRFs) has focused researchers’ attention on the issue related to both the control of the structural integrity and resistance conservation against static incipient collapse in the aftermath of earthquake events. In fact, a huge amount of permanent lateral deformations owing to design-based earthquakes in structures may put residents’ safety at risk even though the repercussions of overall or partial structural damage are not serious. In this case, there is a remote possibility that these impaired structures still remain in operation.
Nevertheless, apparent lack of knowledge in conventional performance evaluation procedures to incorporate the negative impact of residual drifts (RDs) into building code provisions has been recognized. The underlying trend toward defining criteria in performance assessment guidelines is based on the limitation of maximum deformations in each structural component to acceptable level. While several post-earthquake investigations have revealed that the cost of repair or strengthening of buildings suffering from a tremendous amount of RD or permanent displacement is unreasonable. As a result, maximum deformations in conjunction with residual deformations play crucial parts in assessing the seismic performance of structures.
Several investigations follow the growing trend in reducing RD in buildings by means of adding complementtary resisting systems to the primary structures [1,2]. The main objective of these studies is to demonstrate the ability of complementary systems to increase either overall post-yield stiffness ratio or seismic resistance of the primary system. The effects of increasing post-yield stiffness ratio to control the residual displacements of singledegree-of-freedom (SDOF) systems have been examined by MacRae and Kawashima (1997). This study has indicated that residual deformations are highly reliant upon the post elastic stiffness which may be constituted by either positive or negative values. Regarding unfavorable amount of post-yield stiffness in buckling-restrained braced frames (BRBFs), attaching some MRFs to BRBFs has a beneficial effect on mitigation of permanent displacements [3]. From experimental standpoint, a number of researchers have put to use some special post-tensioning techniques as energy dissipation devices which have worked wonders for rooting out permanent drift in MRFs [4-6]. Similar to the results obtained from aforementioned investigations, marked increase in the amount of post-yield stiffness ratio due to applying high-strength strands mainly lies at the root of decrease in permanent displacements [5]. Recognizing high likelihood of RD variations under different seismic hazard levels, recent developments take probabilistic-based concept into consideration when performance-based assessments in buildings have been addressed [7,8]. Regarding system level studies, it has been deemed that several factors directly associated with the variability of ground motion parameters and the inherent characteristics of MDOF systems have profound implication for amplitude and allocation of RD demands [9]. Besides, it is noteworthy that the type of hysteretic models in systems exhibiting stiffnessdegrading behavior considerably influences the level of residual deformation demands [10,11]. In addition to effects of material nonlinearity which was referred above, some sorts of geometrical nonlinearities in terms of socalled P-Δ effects in framed structures drastically alter the amplitude and height-wise pattern of RDs. Several investigations have revealed that P-Δ has adverse effect on completely eliminating positive post-yield stiffness ratio contributing to widespread amount of irrecoverable displacements [1,12]. In this regard, innovative approaches should be geared towards reducing the negative conesquences of P-Δ effects in raising residual deformations.
In this paper using reduced beam section (RBS) connections in MRFs are studied to achieve such reductions, with the purpose of increasing in overall ductility capacity and decreasing in severe loss of overall strength corresponding to P-Δ effects. Up to now, several investigations have been carried out to present the effects of RBS connection on overall response of MRFs [13-15]. In fact, the highly desirable performance distinguished RBS detailing from other connection designs in the aftermath of Northridge earthquake [16-19]. In the paper developed by Kildashti and Mirghaderi (2008), the MRFs with RBS connections were compared to the counterparts without RBS. The results have presented more ductility capacity as well as less over-strength ratio. However, the number of stories was not enough to take into account for the dominance of P-Δ effects. Being more influenced by P-Δ effects, a sixteen-story framed structure is considered as an example in the present resarch. To highlight the effecttiveness of RBS connection in reducing residual deformations, suites of 8 earthquakes representative of pulse-type characteristics in velocity time history from near field motions are taken into account. Of particular interest is to assess the quantity and height-wise pattern of maximum drifts and RDs due to several strong ground motions.
2. The Sixteen-Story Framed Structure Used in This Study
In this study, in order to assess the desired effect of RBS connections in mitigation of RD demands, a sixteenstory framed structure has been taken into consideration. The frame is from a steel building representing identical lateral bearing capacity in two orthogonal directions that it was originally introduced by Jin and El-Tawil (2005). A clear distinction has been drawn between the sixteen-story frame comprising RBS connections and the counterpart without RBS to emphasize the effectiveness of RBS connections in altering RD demands. Overall dimensions and section assignments of the frame are shown in Figure 1. It is worthwhile to note that dummy elements observed in Figure 1 have been deemed to accurately capture P-Δ effects owing to gravity loads which were completely discussed by Kildashti and Mirghaderi (2008). Each framed structure (e.g. with or without RBS detailing) has been modeled based on a set of 2D line elements using flexibility-based concepts then by means of state space approach (SSA) static and transient analyses have been carried out. Of particular concern is the choice of an appropriate constitutive model to predict the relationships between stress resultants and generalized strains in grossly nonlinear domains. This model should be adjusted to the framework of the SSA which is currently applied for large inelastic static and dynamic analyses. A well-known generalization of endochronic model is used herein. This model leads to both a smooth hysteretic behavior and a rather well-mannered state space depiction. Moreover, a non-degrading hysteretic relationship which does not indicate early buckling of steel components is assumed. A detailed explanation of analysis process is accessible in the paper developed by Kildashti and Mirghaderi (2008).

Figure 1. Elevation view of the sixteen-story steel frame used in the study.
The numerical building frame model is subjected to a suite of 8 single-component near-field ground motions. The reason why near-field records have been considered predominantly lies behind their negative impact on increasing RDs [2]. The set of acceleration spectra are scaled in amplitude to correspond with the site specific design spectrum in predefined period range followed by the recommendation of ASCE41 (2006). In particular, the acceleration records have been scaled in which average value of 5%—damped spectrum of those records locate above 1.3 times 5%—damped design spectrum for periods between 0.2T0 and 1.5T0 (T0 is the fundamental period of frame) [20]. The design spectrum has been constructed based on a region located in Los Angeles with seismic parameters as Ss = 2.48 g, Sa = 1.02 g and site class C [21]. Details for all records are provided in Table 1. The pseudo-acceleration response spectra (PSa) from all records are shown in Figure 2. Besides, Figure 3 illustrates the average value of the eight scaled records along with the design spectrum and 1.3 times design spectrum. The average spectrum of eight records is in rationale agreement with 1.3 times design spectrum especially in longer period range, despite the little difference in shorter period range (between 0.6 s and 1.3 s).

Table 1. Near field earthquake records used for inelastic time history analyses.

Figure 2. Pseudo-spectral acceleration of records.

Figure 3. Design spectrum for scaling of acceleration time histories based on ASCE41 (2006).
3. Verification of the SSA in Capturing Geometrically Nonlinear Effects
In this paper, first of all, the capability of SSA to capture large displacement and large rotation characteristics is shown. The reason why this investigation is conducted lies behind the direct link between large deflection characteristics and P-Δ effect which is considered as a key factor on raising residual deformations. It is worthwhile to note that in previous studies, the SSA has been studied in limited geometrically nonlinear problems so its robustness to characterize severe nonlinear conditions with large inelastic deformation features was not completely explored [22,23]. Hence, the efficiency and accuracy of the SSA are validated by the results of numerical simulations based on common examples in the literature.
The first example is the cantilever beam problem subjected to end vertical force as can be observed in Figure 4. Analytical results of this problem with elastic material behavior have been investigated by several authors [24]. The results based on SSA are compared with those proposed by Chan who used elastic perfectly plastic material for two different values of yield stress [25]. In particular, tip displacement in proportion to the beam length is extensively large; therefore, this example is suitable to prove the capability of the SSA to capture large displacement. The results achieved by the example are provided for comparison with those obtained by other researchers [24,25] in Figure 5. It is observed that the SSA shows the high competence in this large deformation problem with only two sub-divisions.
In the second example, the cantilever beam subjected to moment at tip end as shown in Figure 6 is analyzed and the results are compared with the analytical ones. Several researchers have investigated this problem to check the accuracy as well as efficiency of their proposed formulations for extreme in-extensional bending [26,27].

Figure 4. Cantilever beam subjected to end vertical force.

Figure 5. Comparisons among analysis results of cantilever beam subjected to end vertical force.

Figure 6. Cantilever beam subjected to end moment.
This investigation highlights the capability of the SSA to solve problems of very large rotations provided that the structural members are discretized into adequate sub-elements. Since efficiency and accuracy of the element are pertinent to the number of subdivisions, the problem is examined by different member discretization (i.e. with 2, 4, 8 elements). The horizontal and vertical relative displacements of the cantilever tip end are illustrated in Figure 7. In this case, the bending moment exerted at the tip end increases in terms of load ratio from 0.0 to 2.0; as a result, the cantilever twists twice around its fixed point (i.e. up to 720 degrees). As illustrated in Figure 7, for all subdivisions, the results of relative displacements track realistic exactness up to the deformation equal to a half of a circle. However, with increasing curling, the use of two subdivisions leads to erroneous results and the correct equilibrium paths could not be traced. Alternatively, with four and eight elements, the results of beams twisting twice around the fixed end are shown to be very close to those obtained from analytical ones.
It is noteworthy that the main purpose of using the SSA in current study is inelastic structural analyses with deformations in the range of practical interest not just to solve such aforementioned problems. However, the objective of these examples is to support the claim that the procedure can capture large displacements and large rotations if the structural members are subdivided into small elements.
4. Conceptual Performance of RBS Connection in Reducing Negative Aspects of P-Δ
Several framed structures experiencing plastic deformations during the seismic loading are highly likely to suffer from residual deformations. There are several factors contributing to onset of permanent displacements in structures. Although both certain characteristics inherent in ground motions and component hysteretic behaviors play

Figure 7. Comparisons among analysis results of cantilever beam subjected to end moment.
major part in the variation of residual deformations, the amount of permanent displacements is highly sensitive to P-Δ effects. As a result, RDs are largely dependent on P-Δ effects. The positive approach to enhance the capability of structural system to withstand drastic permanent deformations is to implement RBS detailing in MRFs instead of traditional connections. As mentioned in previous paper (Kildashti and Mirghaderi, 2008), RBS detailing has the profound influence on the variation of characteristic features associated with structural overall response. In Figure 8, the variation of base shear force versus center-of-force displacement for assumed frames with and without RBS detailing is schematically illustrated based on the multi-linear assumption. The Center-of-force displacement is chosen at the top of the frames. As can be seen in Figure 8, the positive aspects of RBS frames compared to non-RBS ones are attributed to both more extension to the ductility capacity and less sharpness of falling trend ( ) after the post-peak strength. Additionally, clear trend In Figure 8 illustrates that non-RBS frame involves more over-strength ratio due to higher post-yield stiffness compared to RBS frame (
) after the post-peak strength. Additionally, clear trend In Figure 8 illustrates that non-RBS frame involves more over-strength ratio due to higher post-yield stiffness compared to RBS frame (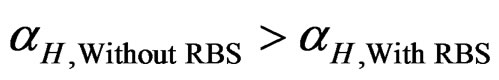 ). As can be concluded from several investigations in the literature, the more post-yield stiffness ratio represents the less residual drift. This feature implies that frame with RBS detailing may be responsible for more RDs rather than the counterpart without RBS owing to less overstrength ratio. However, beneficial aspects of RBS assembly outweigh its shortcoming to mitigate residual drift as the remainder of this paper concerns.
). As can be concluded from several investigations in the literature, the more post-yield stiffness ratio represents the less residual drift. This feature implies that frame with RBS detailing may be responsible for more RDs rather than the counterpart without RBS owing to less overstrength ratio. However, beneficial aspects of RBS assembly outweigh its shortcoming to mitigate residual drift as the remainder of this paper concerns.
With regard to emphasize the influence of RBS connection on reducing P-Δ effects, the sixteen-story frame is investigated based on so-called “pushover analysis”. Uniform load pattern is taken into consideration aimed at more involvement of lower stories to highlight P-Δ effects. In Figures 9 and 10, the inter-story drift ratio in

Figure 8. Multi-linear representation of force-displacement of frames with and without RBS connection.

Figure 9. Contribution of story drift to global response— “Frame without RBS”—uniform load pattern.

Figure 10. Contribution of story drift to global response— “Frame without RBS”—uniform load pattern.
terms of inter-story drift angle divided by roof drift angle as a function of roof drift angle along with pushover curves for RBS and non-RBS frames are illustrated. Pronounced downward trend in pushover curves after the post-peak strength to total loss of strength (collapse stage) arises from the both P-Δ effects in parallel with inelasticity. Since base shear strength are mainly affected by the strength of lower stories, these stories play a crucial role in overall response. It is of interest to note that the inelasticity tends to accumulate around lower stories which represent more involvement in P-Δ effects. So when P-Δ effects are taken into consideration, downward branch of push-over curves has a drastic tendency to fall due to large amount of inelasticity.
Besides, the height-wise contribution of each story to global drift of the frames can be observed in Figures 9 and 10. Comparison between figures indicates that in yielding branch some upper stories participate more in global drift that lead to increase in overall ductility of the RBS frame. In other words, frame without RBS on yielding plateau constitutes story drift angle/roof drift angle between 1 and 3 within first four stories in Figure 9 while frame with RBS on yielding plateau constitutes drift angle/roof drift angle between 1 to 2.5 within first six stories in Figure 10. Subsequently, in descending branch where the P-Δ effect becomes more dominant, the frame with RBS assembly significantly benefits from the contribution of upper stories compared with the frame without RBS. This phenomenon can help to clarify why the pushover curve in frame with RBS detailing has a tendency to be milder in downward branch. Being subjected to lower amount of deformation demands, lower stories in frame with RBS detailing are less susceptible to be involved much in residual drifts.
5. Results of Nonlinear Dynamic Analyses
Of particular aspect in this study is to acquire knowledge about the variation of maximum and height-wise pattern of RD demands in designated frame in the presence of RBS assembly subjected to several earthquake ground motions. To achieve this aim, some sorts of quantities in terms of maximum inter-story drift demands, maximum residual drift demands, and cumulative energy dissipation are investigated in the sixteen-story MRF with and without RBS connections. For comparison, distribution of maximum drifts along the height of both frames is illustrated in Error! Reference source not found. As can be seen, in almost all earthquake records, bottom stories compared to top stories in frame without RBS detailing reflect more contribution to the amplitude of drift. This form of performance indicates that the P-Δ effects are more pronounced and some lower stories have gone through the descending branch of behavior. The overall trend means that although the frame may withstand dynamic instability during strong ground motion, it is more susceptible to static instability until the end of earthquake events. Nevertheless, in the frame with RBS assembly, the participation of the lower stories in overall response of the frame is apparently improved. As can be expected, the frame with RBS detailing are less vulnerable to be on the verge of instability owing to P-Δ effects rather than the other counterpart without RBS.
Similarly, as can be observed in Figure 11, the main RD tends to accumulate over lower stories for both frames with and without RBS assembly. However, this trend towards RD to concentrate in bottom stories is more conspicuous for non-RBS frame than for RBS frame. The rapid growth in RD demands in the lower stories stems from P-Δ effects. It is also of interest to note that RBS frame largely incorporates upper stories into residual drift according to better distribution of inelasticity along the height of frame. Note that, residual drift profile remarkably resembles the overall trend observed for maximum inter-story drift (in Figure 12) for both frames with and without RBS detailing. This resemblance states when extensive residual drift is triggered by P-Δ effects, lower stories are severely impaired by maximum drift demands so the frame experiences an irreversible configuration in the aftermath of the earthquake events. In other words, it is highly likely that the frame is vulnerable to imminent collapse. Nonetheless, as can be seen in Figures 11 and 12, it is evident that both maximum drifts and RDs are diminished by the superiority of RBS connections.
To emphasize the nature of ground motions on the amplitude and height-wise pattern of RDs in both frames with and without RBS connections, a suitable parameter named intensity measure (IM) is defined according to what is mentioned by Ruiz-Garcia and Miranda (2006). In this study, the IM is known as a ratio of maximum inelastic displacement to yield displacement (i.e. ) of equivalent elastic perfectly plastic SDOF system with fundamental period of vibration similar to the frame under consideration. To obtain Δy (yield displacement of SDOF), pushover analysis based on modal load pattern has been taken into consideration. The influence of the relative intensity on RDs along the
) of equivalent elastic perfectly plastic SDOF system with fundamental period of vibration similar to the frame under consideration. To obtain Δy (yield displacement of SDOF), pushover analysis based on modal load pattern has been taken into consideration. The influence of the relative intensity on RDs along the

Figure 11. Sixteen-story MRF with and without RBS connection subject to different earthquake suite; Residual inter-story drift ratio.

Figure 12. Sixteen-story MRF with and without RBS connection subject to different earthquake suite; Maximum inter-story drift ratio.
height for both types of frame with and without RBS is illustrated in Figures 13 and 14. As can be seen, the role of IM in altering RDs is clearly evident. Being influenced by more IM, RD accumulation is drastically increased in lower stories. This observation is valid for both RBS and non-RBS frame. However, RBS frame exhibits more flatten RD profile than non-RBS frame. This observation means that more stories in RBS frame than in non-RBS frame would undergo plastic deformation as the relative intensity rises. In particular, it can also be observed that RD demands of non-RBS frame grow at a faster rate than that of RBS frame especially at bottom stories as the relative intensity increases.
Another noteworthy point is that the frame without RBS detailing almost tends to exhibit greater value in terms of the average ratio of residual drift to maximum drift than the frame with RBS detailing particularly in lower stories as can be observed in Figure 15. This observation means that maximum drift is relatively less reduced in comparison with RD in the RBS frame, thus this fact leads to the major difference of residual/maximum drift ratios in RBS and non-RBS frames. For example, the first story of non-RBS frame constitutes the average residual/maximum drift ratio around 0.8 while that of RBS frame accounts for around 0.6 of this ratio.

Figure 13. Sixteen-story frame without RBS connection.

Figure 14. Sixteen-story frame with RBS connection.

Figure 15. Sixteen-story MRF with and without RBS connection subject to different earthquake suite; Average residual/maximum inter-story drift.
By contrast, in upper stories higher mode effects are more pronounced so the change in the ratio of residual/ maximum drift between the RBS frame and the non-RBS frame is fluctuated. For example, in eighth story the ratio of residual/maximum drift in non-RBS frame is slightly more than RBS frame, whereas the reverse is valid for ninth story. In fact, the superiority of RBS detailing in mitigation RDs is mainly apparent in P-Δ-dominated parts of frames, especially bottom stories, excited more by ground motion.
It is worth noting that cumulative energy dissipation along with deformation demands play a significant role in fully characterizing damage in structures. As shown in Figure 16, the RBS frame has the capability for better distribution of cumulative energy dissipation over the height compared to the non-RBS frame. This clear trend reflects that in non-RBS frame a great deal of cumulative energy move towards lower stories which, as mentioned previously, highly suffer from RDs. Recognizing structural damage indices has a direct relationship with dissipative energy, structural component in lower stories tend to concentrate high level of damage index. In contrast, as can be observed in Figure 16, the significant contribution of middle and upper stories are well-balanced in the energy dissipation that once again emphasizes profound effectiveness of RBS detailing in structural behavior due to favorable distribution of ductility demand.
Figures 17 and 18 show the displacement time histories of several stories of both types of frames with and without RBS connections subject to the record Q2. Implementing the RBS does not enormously change the shape of the displacement, however, does limit the asymmetrical shape of lateral displacements in the inelastic cycles. It is worthwhile to note that the reduced RD behavior during the time history is comparable to the results obtained through previous parts of the paper. This observation means that RBS assembly without further increase in post-yield stiffness ratio just by lengthening

Figure 16. Sixteen-story MRF with and without RBS connection subject to defferent earthquake suite; Cumulative energy dissipation.

Figure 17. Sixteen-story frame without RBS connection.

Figure 18. Sixteen-story frame with RBS connection.
ductility capacity and by softening the negative impact of P-Δ, deserves thoroughly consideration to mitigate residual deformations.
6. Conclusion
In this paper, the influence of so-called RBS connections in reducing the amount of residual drifts mainly owing to P-Δ effects has been investigated. As concluded in several studies, residual drifts are considerably influenced by P-Δ effects. So, use of RBS detailing which contributes to better distribution of ductility demand over the height of the structure leads to diminish the amount of both P-Δ effects and residual drifts, simultaneously. The results of such claims have been confirmed by non-linear transient analyses of sixteen-story frame structures based on scaled near-field ground motions. The results have indicated that the use of RBS assembly is responsible for less involvement of lower stories which plays the major factor in growing residual drifts. As expected, with increasing in the intensity of ground motion, the amount of residual drifts is clearly pronounced. While frame without RBS detailing with increasing in intensity has demonstrated the sharp peak in residual drifts, another counterpart with RBS have had a tendency to smoothly-distributed the residual demands along the height. In addition, both the maximum drift and cumulative energy dissipation as major parts in assessment of damage indices in current performance-based design procedures have substantially fallen in RBS frame rather than non-RBS frame.