A New Proof for the Tight Range of Optimal Order Quantities for the Newsboy Problem with Mean and Standard Deviation ()
1. Introduction
The classical newsboy problem assumes that there is a single purchase decision before the selling season and the demand D is an unknown random variable. The objective is to decide the order quantity Q to maximize the expected profit. In Newsboy problem, the expected profit can be expressed as
 (1)
(1)
where c > 0 is the unit cost, p is the selling price, s is the salvage value, G is the cumulative distribution function of demand. In (1),  is the expected value and
is the expected value and  is defined as
is defined as  when Q is greater than D and zero otherwise. Furthermore, let p = c(1 + m) > c where m is the mark up, and s = (1 – d)c < c where d is the discount, (1) can be expressed as
when Q is greater than D and zero otherwise. Furthermore, let p = c(1 + m) > c where m is the mark up, and s = (1 – d)c < c where d is the discount, (1) can be expressed as

To maxmize the above expected profit , it is equivalent to mininize the following cost function
, it is equivalent to mininize the following cost function
 (2)
(2)
To determine the order quantity Q, G is frequently assumed to be normally distributed in many OM/OR literatures ([1-3]). However, this assumption may not be true in many situations. Technically, it is much harder to obtain the entire distribution information than only part of the distribution information such as mean and standard deviation of G. Scarf [4] first used the min-max approach to find the distribution-free order quantity based on only finite mean µ and standard deviation . The order quantity is given by
. The order quantity is given by
 (3)
(3)
In 1993, Gallego and Moon [5] reproved Scarf’s rule with a compact new proof. They also extended the above analysis to other situations such as the recourse case (there is a second purchasing opportunity), the fixed order cost case, the case of a random yield and the multi-item case where multiple items compete for a scare resource. Moon and Choi [6] extended Scarf’s rule to the newsboy problem with balking. Applications of Scarf’s order rule can also be found in many other inventory models, see for example, [7-10].
2. The Tight Range of Optimal Order Quantities
Consider a family of distributions  with common mean and standard deviation. Scarf’s order rule is based upon the least favorable distribution in the family
with common mean and standard deviation. Scarf’s order rule is based upon the least favorable distribution in the family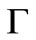 , which minimizes the objective function for any given Q. However, there are infinite distributions with common mean and standard deviation in
, which minimizes the objective function for any given Q. However, there are infinite distributions with common mean and standard deviation in  and each distribution has its optimal solution. Therefore if we can obtain a tight range of the optimal solutions in family
and each distribution has its optimal solution. Therefore if we can obtain a tight range of the optimal solutions in family  and find the relationship between the Scarf’s rule and this range, we can better understand the distribution free Newsboy problem and the demand distribution information’s value. The question of the tight range of optimal order quantities for all distributions in the family
and find the relationship between the Scarf’s rule and this range, we can better understand the distribution free Newsboy problem and the demand distribution information’s value. The question of the tight range of optimal order quantities for all distributions in the family 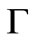 is answered by the following theorem.
is answered by the following theorem.
Theorem. For any , the optimal order quantity G* must be between the tight range [Ql, Qu] where the lower bound is
, the optimal order quantity G* must be between the tight range [Ql, Qu] where the lower bound is
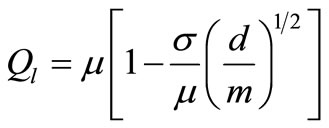
and the upper bound is

Coincidently, Scarf’s order rule is the midpoint of this tight optimal solution range.
In our previous research [11], we focused on the expected value of the distribution information and provide an indirect proof of optimal solution range based on the upper and lower bounds of the objective functions. The question here is if there is a direct proof of the above theorem only based on the definition of the optimal solution. We provide such a direct proof below.
Proof: For a cumulative distribution , if Q* is the optimal order quantity which minimizes C(Q) in (2), then Q* must satisfy the relation that the first derivative of C(Q) is zero. We have
, if Q* is the optimal order quantity which minimizes C(Q) in (2), then Q* must satisfy the relation that the first derivative of C(Q) is zero. We have
 (4)
(4)
If demand D is a continuous random variable, Q* satisfies (5) when the first derivative of (4) is set to be zero. We have
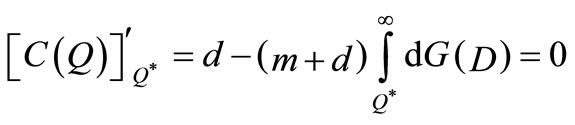 (5)
(5)
That is,
 (6)
(6)
When D is discrete, for general G(D), Q* is an optimal order quantity if and only if either 
or
 ,
,  , (7)
, (7)
where  > 0. In general, no matter D is continuous or discrete, the necessary condition of the optimal order quantity is
> 0. In general, no matter D is continuous or discrete, the necessary condition of the optimal order quantity is
 (8)
(8)
To determine the range of optimal order quantities, it is equivalent to find the smallest (and the largest) Q* which satisfies condition (8), and simultaneously show that the distribution G is in . To find such a smallest Q*, we have the following optimization formulation:
. To find such a smallest Q*, we have the following optimization formulation:
 (9)
(9)
s.t.
 (10)
(10)
 (11)
(11)
 (12)
(12)
It is easy to verify that for a two point distribution with weight [m/(m + d)] on Ql and weight [d/(m + d)] on Qu any Q between Ql and Qu is an optimal solution since it satisfies condition (7}). Therefore Ql and Qu are two achievable optimal order quantities. We now prove that an optimal Q* can not be outside of [Ql, Qu]. Assume that (Ql – ) (where
) (where  > 0) is an optimal order quantity for a cumulative distribution function
> 0) is an optimal order quantity for a cumulative distribution function , from (10) we have
, from (10) we have
 (13)
(13)
From (11) we have
 (14)
(14)
Also,
 (15)
(15)
From (12) we have
 (16)
(16)
and
 (17)
(17)
From (13), (14), (15), (16), and (17), the cumulative distribution function G1(D) must simultaneously satisfy:
 (18)
(18)
 (19)
(19)
and
 (20)
(20)
We have
 (21)
(21)
According to (18) and (19), we have
 (22)
(22)
and
 (23)
(23)
Use the fact that
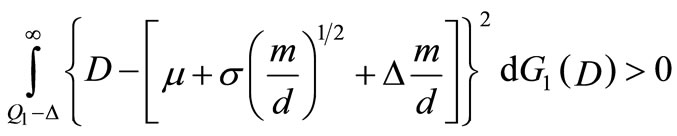
combine with (22) and (23), (21) becomes

This contradicts (20). Therefore Ql – (with
(with  >0) cannot be an optimal order quantity for
>0) cannot be an optimal order quantity for . Similarly, we can prove that optimal order quantity cannot be larger than Qu. To prove this optimal solution range is a tight range, we consider a two point distribution with the weight of [m/(d + m)] at point Ql and weight of [d/(d + m)] at point Qu, we can easily verify that this two point distribution is in the family of
. Similarly, we can prove that optimal order quantity cannot be larger than Qu. To prove this optimal solution range is a tight range, we consider a two point distribution with the weight of [m/(d + m)] at point Ql and weight of [d/(d + m)] at point Qu, we can easily verify that this two point distribution is in the family of , and has the optimal solution at any point between Ql and Qu.
, and has the optimal solution at any point between Ql and Qu.
End of Proof
To obtain a distribution free, and robust order quantity based upon the range of optimal order quantities of [Ql, Qu], one can simply use the average of Ql and Qu. We can see that the robust order quantity is exactly the same as Scarf’s order quantity. Therefore, Scarf’s order quantity is not only the solution of the min-max approach, but also the mid-point of the range of optimal order quantities. This provides an added dimension of our understanding of Scarf’s order rule as the optimal rule based on a distribution free procedure.
3. Conclusion
This Research provides a new direct proof of the tight range of the optimal solution range for the Newsboy problem with only demand distribution mean and standard deviation available. This new proof only uses the definition of the optimal solution. The Scarf’s order rule turns out to be the midpoint of this tight range and which is another indicator of the robustness of the Scarf’s rule. In practice, if only the demand distribution mean and standard deviation are available, we can find the upper and lower bounds of the optimal solution range and compare them with the Scarf’s rule. If the range is not too large, order decision by Scarf’s rule will be a good decision. If the range is very large, Scarf’s rule will be very risky and it is recommended to obtain the entire distribution information to decide the order quantity.