1. Introduction
Orthogonal Frequency Division Multiplexing (OFDM) is a well-known technique. Its main characteristics are the excellent resistance to channel fading and the efficient spectral utilization. The last feature is based on the idea that a data sequence is converted to parallel sequences and in turn these produced streams are distributed in various frequency carriers. Moreover, another interesting fact is the term of Orthogonality when is added to FDM. The functionality of this term ensures that all produced frequencies are harmonic to a primary one and in this way they can’t interfere with each other theoretically. Practically various safe precautions should be taken such as ZP (Zero Padding) or CP (Cyclic Prefix) [1]. Specifically, CP is a technique of increasing the symbol’s duration by copying a part of its end to its front region. Hence, CP can be inserted only once to every OFDM symbol. As for the ZP, its presence ensures the recovery of a symbol which has been transmitted over a noiseless environment even if the channel has zero locations. The previous fact does not apply in the case of CP. Nevertheless in more noisy conditions the better performance of ZP-OFDM towards CP-OFDM decreases due to ZPOFDM’s lower energy. So, the performance relies on the guard length [2]. Taking into consideration the previous fact that ZP case is better than CP with drawbacks [3], we decided to combine double ZP (end and beginning of the signal before IFFT) with CP (after IFFT).
OFDM has been vastly recognized through its adaptation by many standards and applications. These are included in WiMAX, High-Performance LAN type 2 (HIPERLAN/2), Digital Subscriber Lines (DSL), and others [4]. Also, similar applications utilize Turbo codes such as digital TV, Wireless LAN and fading channels [5]. Hence, we must not omit the fact that the Turbo codes can be implemented in OFDM systems [6] which was one of the purposes of this research followed by the investigation of our PCCC design’s performance. The latest was compared to other Turbo schemes. These Turbo schemes were already known techniques such as Parallel concatenated convolutional codes (PCCC) and Serial concatenated convolutional codes (SCCC). Their functions depend on weather the convolutional encoders in the design are joined in parallel or in serial for the construction of the final code. Also, not all convolutional encoders accept the same primary data. In each case one accepts the random information straight from the generator while the other, accepts the interleaved data version (PCCC case) or the interleaved output of the outer encoder (SCCC case). As for the decoder’s section, it is constituted of APP (A Posteriori Probability) decoders which are connected through a feedback loop. This loop is the iterative function of the decoding part. The primary idea behind this mechanism is the better evaluation of the data when they pass for another time through APP decoders. Consequently, the natural assumption is that Iterative decoding outperforms Viterbi decoding, which is true and wellknown [7].
Furthermore, Iterative Decoding [8] is also an integral function of our new scheme of PCCC [9] which we inserted in our OFDM system with the appropriate modifications. This PCCC technique is constituted of three parts. The fist part is associated with the encoding procedures. These are conducted by three convolutional encoders, which accept the data straight from the source (first) or through an interleaver (second) or through two consecutive interleavers (third). Then all the encoders’ outputs are concatenated in parallel. The second part is associated with the distribution of the original stream of information (which has passed through an AWGN channel) to three outputs which are connected to the appropriate APP decoders. These are integral components of the decoder’s system and constitute the third part.
Two types of Turbo techniques and our PCCC scheme are mentioned in the second part of this publication along with the relevant theory of operation. The third part is involved with the description of our OFDM system’s architecture. The fourth section presents the simulation parameters and the BER results for all simulated systems. Apart from the fact that all Turbo Coded OFDM schemes show excellent performance compared to Convolutional Coded OFDM, the proposed design clearly outperforms all of them.
2. Turbo Codes—Description and Operation
Coding theory exhibits in the bibliography various methodologies which were invented for the purpose of boosting the performance of a link. The most powerful techniques have proven to be those that utilize a combination of convolutional codes. Turbo codes [10] employ the previous method. These codes can be PCCC or SCCC. These schemes also use a number of interleavers for disassociating various data streams in a design. Several types of these interleavers have been proposed and developed with the most dominant to be its Random version [11].
The convolutional encoders which were used in this study are two already known types. The first type obtains a code rate of 1/2 with constraint length 3, memory which equals to 2 and generator polynomials 78 and 58 (in octal form) and with a feedback loop of 7. The second type with a constraint length vector of (3, 3) has a code rate of 2/3 with matrix of generator polynomials (78 08 58, 08 78 68) with feedback loop vector of (7, 7) and total memory size of 4.
The SCCC encoder contained the two previous types of convolutional encoders in serial, which were joined through a random interleaver (Figure 1). The outer encoder corresponds to the first type and the inner to the second type. So, the final formed encoder system is considered to have a constraint length of 7, with memory size of 6 and a code rate of 1/3. Furthermore, the PCCC were adjusted to consist of only the first type of convolutional encoder. The design of Parallel Turbo codes [12] contained two (Figure 2) [13] or more [9] convolutional encoders in parallel. In every design, one of them received the data stream straight from the random generator, while the others accepted an interleaved version of the primary generated data. Especially inside our encoder, a third convolutional encoder was joined with the data generator through two random interleavers as it appears in Figure 2. Hence, three interlacers were employed in the design instead of two (in typical case). These interlacers distributed the incoming information in two outputs. Their purpose was to provide a systematic and a recursive version of the input. Specifically, in the typical parallel system two interlacers provided three outputs, which one of them was the systematic while the other

Figure 2. Parallel turbo encoder design (the additional blocks with grey color are needed in order to obtain a code rate of 1/4 instead of 1/3 with the same conv. encoder).
two were the recursive versions. Moreover, in our encoder an additional puncture block produced another recursive signal. Finally all the outputs were concatenated in parallel using horizontal concatenation, transposing and reshaping. Also, it must not be neglected the fact that the typical PCCC encoder had a code rate of 1/3 (one systematic and two recursive) while our encoder had a rate of 1/4 (one systematic and three recursive).
Turbo technique in its iterative section contains APP decoders [14]. These APP decoders employ the A Posteriori Probability function. Generally, the APP function of an event has a direct relation with another event’s operation. The previous condition applies only when the two events happen at the same time. The previous APP decoders are usually found in pairs in the iterative sections of SCCC (Figure 3) and PCCC. The first APP block (for SCCC case is named inner) accepts the coded sequence which has passed through an AWGN channel and its other input is connected to the iterative section. The output of the inner is joined to the outer decoder. In turn, the outer decoder’s outputs are connected to the hard decision block (for the production of 0’s and 1’s) and to the feedback section. Other blocks such as Gain and Unipolar to Bipolar converter are used in the same manner as in [15].
PCCC require prior to their decoding procedures [16] a puncturing process. This process is conducted in order to produce two types of convolutional encoders’s outputs. These types are the systematic and recursive versions. Then, these data sequences are interlaced. The interlaced outputs are connected to APP decoders’ inputs. Furthermore, for the case of our coding system [9], additional blocks are needed and they are grey colored as it shows in Figure 4.
Interleavers and deinterleavers are included in the APP decoders’ section. Interleavers, which are placed between APP blocks, create statistical independence of their inputs. Then the data are ready to be compared with the original data stream as soon as they pass through a deinterleaver followed by the Hard Decision [17] block for taking the form of 1’s and 0’s (Figure 5). Similarly, our final decoder’s part (Figure 6) has three APP blocks instead of two. Moreover, the total number of the interleavers which are placed between the APP decoders is two. So, in the feedback section there is a delay function, a pulse generator and a product block along with two deinterleavers. The reason for using the last as a pair is that the data stream inside the final decoder’s section has been interleaved two times. So, in order this stream to start another loop it must pass through the iterative section and reach L(u) input in its primary level of association with L(c) input of APP decoder 1.
3. Architecture of the Turbo Coded OFDM
A Coded OFDM apart from the final production of the multicarrier transmission it exhibits excellent BER performance. The data sequence is generated with a 50% probability of zero. Also, the sample time is related with the block size and an additional factor. This factor is changed by the user every time a different block size is utilized for the purpose of transmitting the same number of bits. Then the produced signal passes through the encoder’s stage. This stage could use PCCC, SCCC or
Convolutional Codes. The output from the previous stage is joined with a modulator. For this research QPSK is selected and in turn each symbol is constituted of two bits. Then, the frame conversion and unbuffering procedure are used in order the data stream to be buffered to the appropriate size. This size is 75% of the total carriers’ number in the output of IFFT block. The remaining 25% is used for zero padding [18]. This is applied at the end and at the beginning of the signal by adding zeros. In this point all the desirable characteristics of the signal have been set. Hence, the signal passes through IFFT block. This block is very crucial as it ensures the orthogonality feature for all produced carriers [19,20]. Then, Cyclic prefix (25% of IFFT output) is appended to the OFDM symbol while serial to parallel conversion is conducted for enabling the transfer of the signal through the AWGN channel (Figure 7).
When the signal reaches the receiver’s end, the reverse procedures will be initiated. The signal will be buffered at the nominal value of 125% of the carriers’ number (at the output of IFFT). Also, cyclic prefix will be removed and Fast Fourier Transform (FFT) will be conducted (Figure 8). A function of unbuffering and buffering will be applied after the last section. Moreover, the buffer’s size must be equal or greater than the block size (Table 1) in order the dimensions of the signal to change accordingly. Then, this will pass through the demodulator for being decoded. Finally, the signal has the appropriate

Figure 8. Stage of FFT and guard band removing.

Table 1. Various delays and buffer sizes.
dimensions in order to be compared to the original pseudorandom version.
Generally, several delays are produced inside OFDM designs by various procedures which take considerable time to be completed. In our design all the previous delays were computed along with the application of a perfect synchronization between transmitter’s and receiver’s stages. Furthermore, our design was flexible enough to permit fast changes in Eb/No, Block size, Iterations’ number and Carriers’ number (at the output of IFFT). Moreover, the additional factor which was mentioned earlier must be altered according to the selected frame size for assuring that each time the same amount of data will be transmitted. A schematic of the previous feature along with the OFDM design is shown in Figure 9. In this figure the Block of “PAD, IFFT, CP” corresponds to Figure 7 and the Block named “REMOVE CP, FFT, REMOVE PAD” is shown analytically in Figure 8.
4. Simulation Parameters and Results
The Coded OFDM which was designed and simulated has various features. One of these features is the production of large number of subcarriers. A typical value of 2048 was selected [21]. This number corresponds to the total carriers which are created using IFFT block. Then, four types of coding systems were simulated. These included PCCC, SCCC, new PCCC design and Convolutional coding (with Viterbi decoder as a reference point, and not SOVA, as the latest involves more complicated procedures and still worst performance compared to PCCC and SCCC) [22].
In all the previous schemes, two types of convolutional encoders with code rates of 1/2 and 2/3 were selected as parts of the designs. Only one of the previous, which had the code rate of 1/2 was used in PCCC, new PCCC and

Figure 9. Turbo coded OFDM system (receiver’s stage is presented with grey colored blocks).
Convolutional Coding. Instead, in SCCC case both types of previous encoders were utilized. In decoders’ stage every APP block was adjusted to utilize the max* algorithm [23]. Hence, the size of the occupied memory of the decoder is reduced and the decoding procedure takes less time to be completed. For the previous reasons we didn’t select True A Posteriori Probability [24]. Furthermore, the puncturing procedure, which is located in the primary stage of decoding, is mentioned in [9].
Also, noise characteristics were included in the configuration of the simulation platform. An AWGN channel was connected between the transmitter and the receiver. This channel can be described with terms of Eb/ N0 (Eb is the energy per transmitted bit and N0 is the spectral density of the noise power). Hence, modulation is directly associated with the number of transmitted bits per symbol. With the presence of a coding system creating a code rate of RM, and noise variance which equals to N0/2, the following Equation (1) can be produced [9], [25].
 (1)
(1)
The previous equation is very important as it calculates the noise quantity which will be added in the signal when it enters the AWGN channel. Also, special care must be taken in order Es to be adjusted to the appropriate value for each case of produced number of subcarriers. The value of Es is found with the proper calculation of signal energy after IFFT block, taking into consideration the percentage of zero padding.
Moreover noise variance is different for various coding schemes and modulation types (Table 2). QPSK was selected as the modulation type. The Rm calculation is very simple and is presented in Equation (2). Furthermore M is the constellation size which equals to 4 for QPSK.
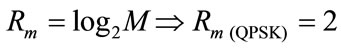 (2)
(2)
The simulation procedures involved the comparison of various coding schemes located inside an Orthogonal Frequency Division Multiplexing (OFDM) system. In turn the previous comparison concluded in finding each time the system’s behavior in terms of BER. The utilized frame sizes constituted of the numbers 64, 128, 256 and 512. In the following figures is presented the BER versus Signal-to-Noise ratio per bit (Eb/N0) for every studied case. These figures include four kinds of curves. Each type corresponds to a frame size. Also, it can be observed that only one curve in every figure remains unchanged as it presents the performance of Viterbi decoding for the highest packet size (512). Moreover, in the following figures, OFDM’s excellent performance is evidenced for three, four and five iterations. Figure 10(a) presents BER
performance (vertical axis starts from 3·10–6) for five conducted iterations except from the case of Viterbi coding where feedback function is not supported. For frame size of 64 the new coding system [9] shows better performance starting from 1.5 dB (Eb/N0) compared to that of PCCC. Then, performance clearly becomes better from the point of 0.5 dB for packet size of 128. Additionally, OFDM system with new Parallel Concatenated Convolutional Codes outperforms all others for the remaining studied frame sizes. Figure 10(b) exhibits simulation results regarding four iterations (vertical axis starts from 4·10–6). Similarly to the previous paragraph, the value of 1.5 dB for block size 64 proves to be the point from which the new system starts to behave better compared to a typical PCCC. Moreover for frame size 128 the new PCCC outperforms typical PCCC (from 0.6 dB). Furthermore, all other cases of packet sizes perform in the same manner to those of the previous paragraph. Finally we reach at similar conclusions when the case of Figure 10(c) (vertical axis starts from 5·10–6) is examined. Also, it must be noted the fact that in cases of 128 and 256 size of packets, the new coding system is better even when it is compared with other coding schemes of higher frame size (e.g. New PCCC with frame size 256 is better compared to a typical PCCC with frame size 512 from 0.6 dB).
5. Conclusions
Orthogonal Frequency Division Multiplexing (OFDM) can be easily implemented due to IFFT and FFT processing. It is also tolerant in multipath fading and exhibits efficient bandwidth. This bandwidth is divided into many subcarriers which can be modulated. Moreover, all the previous subcarriers are orthogonal. This allows the signal processing to be conducted very easily and accordingly leads to overall system simplicity. The previous scheme combined to a Turbo coding technique can lower significantly the received errors. This way a more successful and robust communication can be established. Nevertheless, all previous OFDM advantages are paid with the price of a larger Peak to Average Power Ratio (PAPR) along with the fact that the transmit signal can exhibit an almost Gaussian distribution. Also, spurious transmissions can interfere with the OFDM system. Reducing them is achieved with the insertion of Guard Bands or Windowing. All the above along with the



Figure 10. BER Performance of coded OFDM for (a) 5 iterations; (b) 4 iterations and (c) 3 iterations.
increased complexity of Turbo codes, and a larger constellation (modulation), can constitute a very complicated system from the aspect of implementation or even simulation. So, each time and for a system with different variables, additional research must be conducted. The latest constitutes a future trend on the field in order to achieve minimum complexity, high performance, convenience in simulation and implementation issues. At the same time all the undesirable effects of the utilized schemes must be reduced as low as possible [26]. The previous mentioned are also requirements of Space Time Turbo Coding (STBC) and MIMO applications [27-30].
A new Turbo coding scheme based on Parallel Concatenated Convolutional Codes was become part of an OFDM system which was modified according to the specifications’ needs and addressed many issues of the previous paragraph. Then, all receive delays where computed for every case of inserted coding type. In turn, after the calculation of noise variances, simulation procedures were executed in order to determine the BER performance for all the diversity of Coded OFDMs. The Turbo Coded systems exhibited an excellent tolerance of Additive White Gaussian Noise. New Turbo OFDM dominated all others in terms of BER.
The proposed Turbo Coded OFDM is the fulfillment of one of our goals to incorporate our Turbo coding system in Orthogonal Frequency Division Multiplexing technique [9]. The next part of our research is to enhance even better our system with schemes of reduced PAPR [31], [32] and even go one step further and combine it with UWB technology [33,34]. Finally DSP implementation is also a future target of our research [35].
6. Acknowledgements
This research has been co-financed by the European Union (European Social Fund—ESF) and Greek national funds through the Operational Program “Education and Lifelong Learning” of the National Strategic Reference Framework (NSRF)—Research Funding Program: Heracleitus II. Investing in knowledge society through the European Social Fund.