1. Introduction
In auction markets, such as the NYSE, specialists fix transaction prices after customers have filed their orders. In Pete Kyle’s formulation of a call auction market [1], these agents represent passive agents who set transaction prices according to semi-strong efficiency condition. In this way it is possible to identify linear equilibria and study the characteristics of the market. However, specialists on the NYSE are not mere executors of clients’ orders. Their behavior, as indicated by several empirical studies [2], is active and influenced by risk management considerations. In particular, there is evidence that they are risk-averse, as they set transaction prices to control their inventories and risk exposure.
We show that when specialists are risk-averse the simple linear equilibria of Kyle’s analysis disappear. This holds irrespective of preferences and endowments of market participants or of the degree of informational asymmetry among the specialists and the informed traders. It is the consequence of the particular protocol of trading imposed by Kyle’s framework, where specialists act after their customers. To outline the fragility of such framework is important given the ample attention it has received in the literature.
2. Linear Equilibria with Informative Market Orders
In Kyle’s auction market a specialist trades with a group of customers a numeraire, which pays certain return (normalized to 0), for a risky asset, with an uncertain liquidation value which is normally distributed with parameters 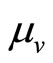 and
and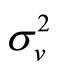 . As we consider the static formulation of Kyle’s model, in period 0 a call auction is run, while in period 1 the liquidation value of the risky asset is publicly announced.
. As we consider the static formulation of Kyle’s model, in period 0 a call auction is run, while in period 1 the liquidation value of the risky asset is publicly announced.
The protocol of trading governing the market corresponds to that of a call auction. Thus, in period 0 the specialist’s customers place their market orders for the risky asset. Customers comprise a population of liquidity traders, which collectively place an uninformative market order, 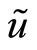 , and an insider who submits an informative market order,
, and an insider who submits an informative market order,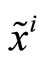 . By convention when
. By convention when 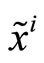 and
and 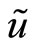 are positive (negative) the specialist’s clients purchase (sell) the risky asset. When submitted, all orders are batched together and passed to the specialist. This means that the specialist only observes an aggregate market order,
are positive (negative) the specialist’s clients purchase (sell) the risky asset. When submitted, all orders are batched together and passed to the specialist. This means that the specialist only observes an aggregate market order, 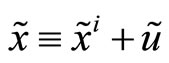 , for the risky security. On the basis of the information contained in the aggregate market order the specialist sets a transaction price for the risk asset,
, for the risky security. On the basis of the information contained in the aggregate market order the specialist sets a transaction price for the risk asset, 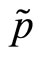 , at which all individual market orders are executed. This price, that we indicate with
, at which all individual market orders are executed. This price, that we indicate with , measures the number of units of the risk-free asset required to purchase one unit of the risky one.
, measures the number of units of the risk-free asset required to purchase one unit of the risky one.
The overall market order of the population of liquidity traders is normally distributed with parameters 0 and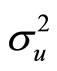 . As usual this order is orthogonal to all other random variables. On the contrary, the insider observes a noisy signal on the liquidation value of the risky asset before any trading takes place. Such signal is equal to
. As usual this order is orthogonal to all other random variables. On the contrary, the insider observes a noisy signal on the liquidation value of the risky asset before any trading takes place. Such signal is equal to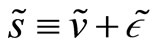 where
where 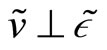 and
and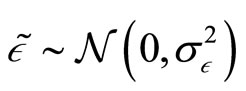 . This implies that the conditional liquidation value of the risky asset given the insider’s private information is
. This implies that the conditional liquidation value of the risky asset given the insider’s private information is


In Kyle’s original formulation the insider exploits her information advantage to gain speculative profits. However, as shown by Subrahmanyam [3], the market equilibrium can be easily characterized even when she is endowed with a standard constant absolute risk-aversion (CARA) utility function with coefficient of absolute risk aversion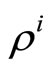 . We allow for both specifications, as our main result holds irrespective of the insider’s attitude towards risk.
. We allow for both specifications, as our main result holds irrespective of the insider’s attitude towards risk.
In Kyle’s original formulation the specialist belongs to a population of risk-neutral market makers. Bertrand competition in the market making industry induces the specialist to break-even and to set the transaction price for the risky asset according to semi-strong form efficiency. We assume instead that the specialist is riskaverse and maximizes the expected utility of his final wealth. We assume that his utility function is a CARA with coefficient of absolute risk-aversion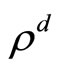 . The specialist’s final wealth depends on his endowment of the numeraire, m, and risky asset, b. Because the specialist is not price-taker, this endowment conditions his choice of the transaction price,
. The specialist’s final wealth depends on his endowment of the numeraire, m, and risky asset, b. Because the specialist is not price-taker, this endowment conditions his choice of the transaction price,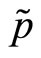 .
.
The insider’s trading strategy, X, defines her market order given the information she possesses,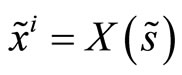 . The specialist’s pricing rule P is function of the order flow he observes,
. The specialist’s pricing rule P is function of the order flow he observes,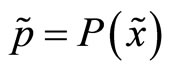 . The players’ final wealth,
. The players’ final wealth,
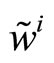 and
and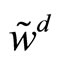 , is function of these two strategies,
, is function of these two strategies, 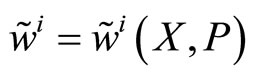 and
and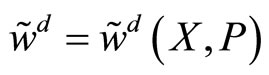 . Their utilities are functions of their strategies and their degree of riskaversion,
. Their utilities are functions of their strategies and their degree of riskaversion, 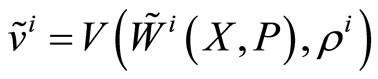 and
and
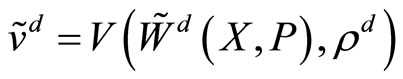 .
.
Since customers can only place market orders, if some restriction is not imposed, the maximization problem of the specialist is unbounded. Then, while the participation constraint for the specialist is
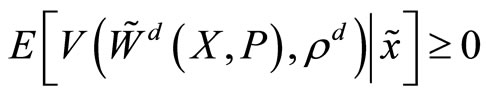 ,1 we assume that competetion in the market making industry drives such expected value to zero.
,1 we assume that competetion in the market making industry drives such expected value to zero.
Given this specification for the two agents’ strategies we modify the equilibrium concept put forward by Kyle.
Definition 1. A Bayesian (Nash) equilibrium for the call auction market with the risk-averse insider and specialist is a pair of strategies (X, P) such that:
1) The insider maximizes her conditional expected utility: 
 (1)
(1)
2) The specialist sets the transaction price to reach the lower bound for the expected value of his utility: 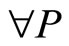 and x
and x
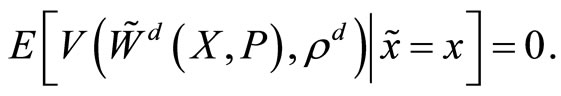 (2)
(2)
Linear Bayesian equilibria respect the following Definition.
Definition 2. A linear Bayesian (Nash) equilibrium is a pair of strategies (X, P) that satisfies Definition 1 such that X is linear in the insider’s signal 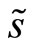 and
and 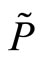 is linear in the market order the specialist observes,
is linear in the market order the specialist observes,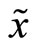 .
.
We are now ready to state our main result.
Proposition 1. A linear Bayesian equilibrium for the call auction market with a risk-averse specialist does not exist.
Proof. Assume that 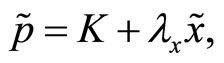 where the constant K depends on the specialist’s initial endowment of the risky asset,
where the constant K depends on the specialist’s initial endowment of the risky asset,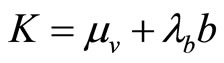 .
.
Assume the insider is risk-averse and chooses her market order maximizing the expected utility she obtains from her final wealth. Without loss of generality assume she does not possess any units of the two assets, so that she maximizes the expected utility of her trading profits. Thus, if her utility function is CARA with coefficient of risk-aversion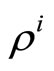 , she solves the following problem,
, she solves the following problem,
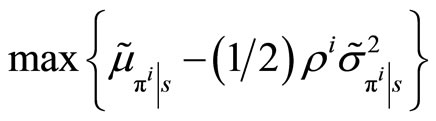 , where
, where 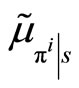 and
and 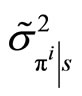 are the conditional mean and variance of her profits,
are the conditional mean and variance of her profits,
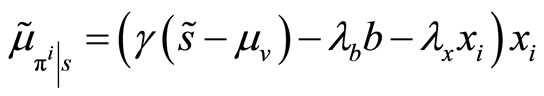 ,
,
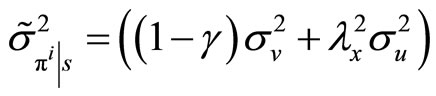 . Her optimal market order is
. Her optimal market order is
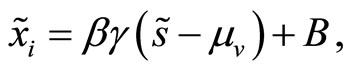 (3)
(3)
where

and
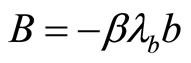 . A maximum is obtained for
. A maximum is obtained for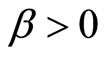 . This is the case if
. This is the case if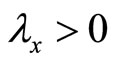 .
.
Suppose then that the specialist sets the transaction price assuming that the market order placed by the insider, 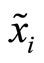 , respects Equation (3) with
, respects Equation (3) with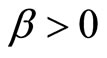 . Hence, the expected mean and variance of his final wealth,
. Hence, the expected mean and variance of his final wealth, 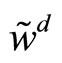 , are respectively
, are respectively 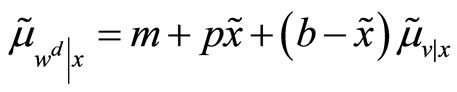 and
and
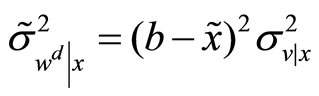 , where applying the projection theorem for Normal random variables we know that
, where applying the projection theorem for Normal random variables we know that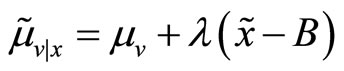 ,
, 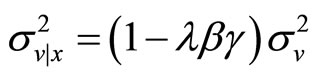 , with
, with
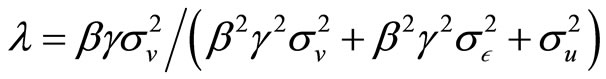 . Given his utility function and the constrain in (2), the specialist sets
. Given his utility function and the constrain in (2), the specialist sets 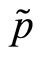 by imposing the following condition
by imposing the following condition
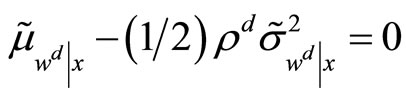 . Without loss of generality suppose that
. Without loss of generality suppose that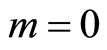 . This just simplifies our algebra, but it is inconsequential for the validity of our main result. Then, it is immediate to see that the transaction price fixed by the specialist is
. This just simplifies our algebra, but it is inconsequential for the validity of our main result. Then, it is immediate to see that the transaction price fixed by the specialist is
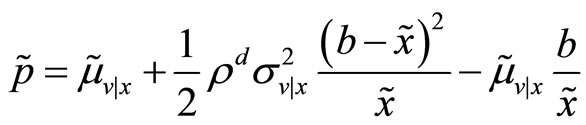 .
.
Substituting the expressions for 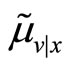 and
and 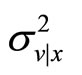 the transaction price is
the transaction price is
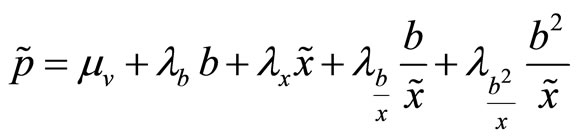 where
where

since the posterior variance 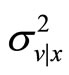 is strictly positive
is strictly positive
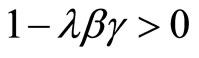 . In addition,
. In addition, 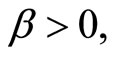 given the definition of λ, we see that
given the definition of λ, we see that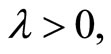
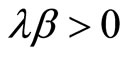 and
and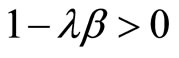 . These inequalities imply that
. These inequalities imply that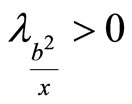 . Since
. Since 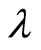 and
and 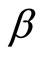 do not depend on
do not depend on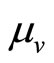 , it is not possible that
, it is not possible that 
so that in the pricing function there is a term in the inverse of the aggregate market order.
The economic intuition for the non-existence of linear equilibria is simple: because of his risk-aversion the specialist tries to manage his inventory of the risky asset and hence, ceteris paribus, charges transaction costs which are not proportional to the size of his customers’ orders.
Interestingly, our result differs from the analysis of Subrahmanyam [3], who considers the case of a riskaverse insider and a risk-averse specialist with a zero endowment of the risky asset and shows that a linear equilibrium indeed exists. The proof of Proposition 1 makes clear that no linear equilibria can exist when the specialist possesses a non-zero endowment of the risky asset, so that Proposition 1 shows how Subrahmanyam’s result is somehow special. With a CARA utility function the well known result that the initial endowment (or wealth) of an investor does not influence her optimal portfolio holds if and only if such investor is price-taker. Such condition does apply to the specialist, so it is not surprising to see that different conclusions are reached when the specialist possesses or do not possess an initial endowment of the risky asset.
A problem with this analysis of the consequences of risk-aversion on the part of the specialist is that the assumption that customers can only place market orders is hard to maintain in the current formulation. When the insider faces a specialist who is free to set the transaction price, she will be willing to trade only if she can condition her order on the transaction price. Indeed, in the NYSE specialists accept both market and limit orders. We now consider the case in which customers can submit limit orders as well.
3. Linear Equilibria with Informative Limit Orders
According to this modified protocol of trading, customers still place their orders for the risky asset at the beginning of period 0, before the specialist sets the transaction price. However, while the liquidity traders place a collective market order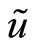 , the insider submits a limit order, i.e. a demand schedule,
, the insider submits a limit order, i.e. a demand schedule,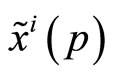 . Now the specialist observes an aggregate demand function,
. Now the specialist observes an aggregate demand function, 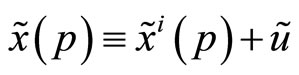 , as on a limit order book.
, as on a limit order book.
Consequently we need to modify the strategy space and the equilibrium concept we employ. Under the new trading protocol a trading strategy for the insider, 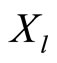 , defines her demand schedule as function of her private signal,
, defines her demand schedule as function of her private signal,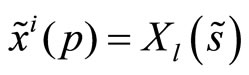 . Similarly, the pricing rule of the specialist,
. Similarly, the pricing rule of the specialist, 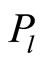 , is a function of the aggregate demand schedule he observes,
, is a function of the aggregate demand schedule he observes,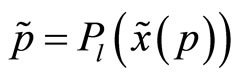 .
.
The insider and the specialist still maximize the expected value of their utilities. However, since the insider can place a limit order the specialist’s optimization problem is well defined and it admits a maximum. We can then define a proper equilibrium concept even if there is no competition in the market making industry. In this section we prove that a linear Bayesian equilibrium does not exist when the specialist is free to maximize his expected utility. A fortiori the same result holds with an upper bound on his expected utility.
To accommodate the new trading protocol we modify the equilibrium concept as follows.
Definition 3. When limit orders are allowed, a Bayesian (Nash) equilibrium for the call auction market with the risk-averse insider and specialist is a pair of strategies 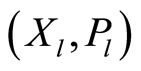 such that the following two conditions hold:
such that the following two conditions hold:
1) The insider maximizes her conditional expected utility: 
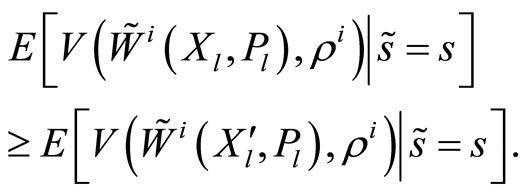 (4)
(4)
2) The specialist maximizes her conditional expected utility: 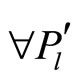 and
and 
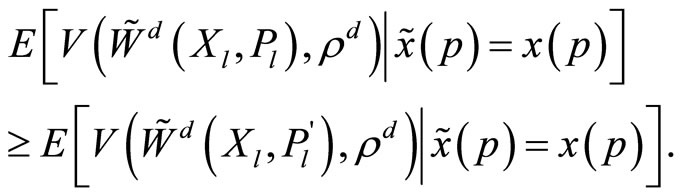 (5)
(5)
when limit orders are allowed linear Bayesian equilibria respect the following Definition.
Definition 4. When limit orders are allowed, a linear Bayesian (Nash) equilibrium is a pair of strategies 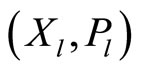 that satisfies Definition 3 such that
that satisfies Definition 3 such that 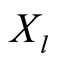 is linear in the private signal of the insider
is linear in the private signal of the insider 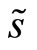 and
and 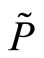 is linear in the aggregate demand schedule the specialist observes,
is linear in the aggregate demand schedule the specialist observes,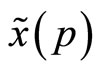 .
.
We are now ready to confirm our main result.
Proposition 2. When the insider can place a limit order, a linear Bayesian equilibrium for the call auction market with a risk-averse specialist does not exist.
Proof. Suppose that the specialist fixes the transaction price assuming that the insider’s demand schedule, in line with Definition 4, is linear in the subjective mispricing of the risky asset,
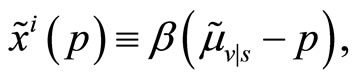 (6)
(6)
where 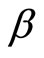 is some constant. Then, the conditional mean and variance of the specialist’s final wealth,
is some constant. Then, the conditional mean and variance of the specialist’s final wealth, 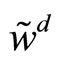 , are
, are

and
 where, applying the projection theorem for Normal random variables, we know that
where, applying the projection theorem for Normal random variables, we know that 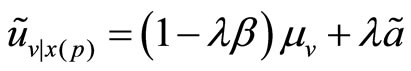 and
and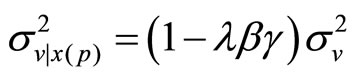 , with
, with
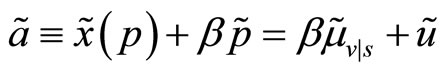 . The specialist fixes
. The specialist fixes 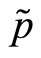 solving the following program:
solving the following program:
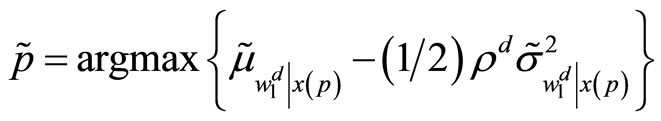 .
.
It follows that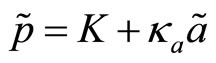 , where2
, where2


Since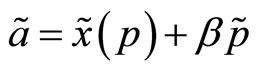 , the transaction price can be written consistently with Definition 4 as a linear function of the aggregate demand schedule,
, the transaction price can be written consistently with Definition 4 as a linear function of the aggregate demand schedule,
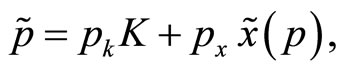 (7)
(7)
where

To check if the demand schedule introduced in Equation (6) is optimal given the preferences of the insider, consider that the conditional mean and variance of her profits, 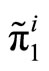 , are
, are 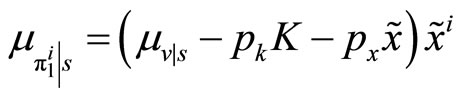 and
and
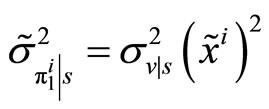 . Given her zero endowment and her CARA utility function she chooses her demand schedule solving the following program:
. Given her zero endowment and her CARA utility function she chooses her demand schedule solving the following program: 
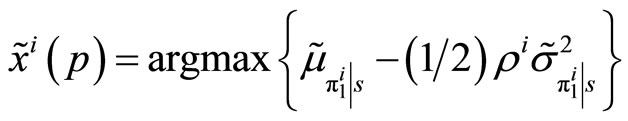 .
.
Considering that the insider can condition on the transaction price, and hence on the realization of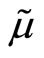 , we find that
, we find that
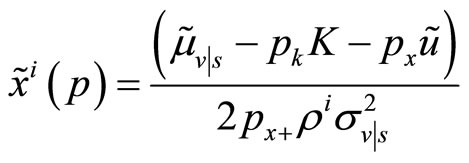
However, given the pricing rule (7), the insider’s demand schedule can be explicitly written consistently with Definition 4 as in Equation (1), where 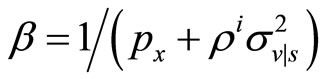 . To have a maximum the second order condition
. To have a maximum the second order condition 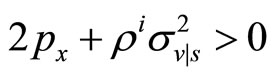 must be satisfied. To check that it holds explicit solutions for
must be satisfied. To check that it holds explicit solutions for 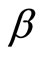 and
and 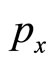 must be obtained. They solve the following non-linear system
must be obtained. They solve the following non-linear system

Substituting 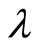 into
into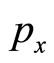 , the resulting expression into that for
, the resulting expression into that for 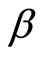 and rearranging it turns out that
and rearranging it turns out that 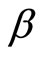 must be a root of the following equation
must be a root of the following equation

This might have either one root or three roots. Beside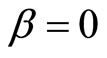 , there might be two extra negative roots. Anyhowit must be that
, there might be two extra negative roots. Anyhowit must be that 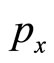 is negative as
is negative as 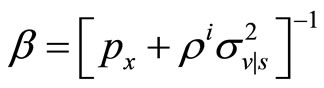
and 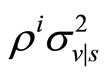 is positive. Hence, in all cases
is positive. Hence, in all cases 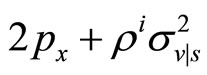 is negative, so that we have a minimum rather than a maximum. In addition, for
is negative, so that we have a minimum rather than a maximum. In addition, for 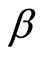 negative the second order condition of the specialist’s program is violated, suggesting that the insider finds optimal to destabilize the market. Thus, a linear Bayesian equilibrium cannot exist! □.
negative the second order condition of the specialist’s program is violated, suggesting that the insider finds optimal to destabilize the market. Thus, a linear Bayesian equilibrium cannot exist! □.
Proposition 2 is reminiscent of Kyle [4] (Theorem 5.1), who shows that a linear equilibrium does not exist in a market with one informed and one uninformed investor. In his formulation these two risk-averse agents act noncompetitively and simultaneously submit demand schedules which are cleared in equilibrium. In the current specification, instead, the specialist acts after the insider to fix a transaction price and clear the market. In practice, Proposition 2 improves on Kyle’s analysis in that it shows how his result is robust to the order of players’ moves.
Whenever the specialist is not forced to set the transaction price according to semi-strong form efficiency, Kyle’s linear equilibrium breaks down. This conclusion holds whatever the insider’s preferences and endowment and whatever the quality of her signal. Our analysis indicates that the market structure in Kyle’s model is not robust, in that it is its protocol of trading, rather than fundamentals, such as the allocation of information and assets or the preferences of the agents, that makes the market unstable.
4. Acknowledgements
I wish to thank the Editor and an anonymous referee for their comments and suggestions. I also thank Luca Panaccione and participants at seminars at the University of Tor Vergata and Luiss University.
NOTES
2For 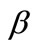 positive the second order condition of the maximization program of the specialist is satisfied.
positive the second order condition of the maximization program of the specialist is satisfied.