1. Introduction
Research in non-linear control theory has been motivated by the inherent characteristics of the dynamical systems to control. Many systems are non-linear, their dynamics are not perfectly known and therefore not exactly modelled. Control engineers have hardly worked to improve the usual control methods as PID in order to guarantee closed loop stability in the presence of unmodeled dynamics and external disturbances. But, despite these efforts, conventional linear control techniques cannot meet all requirements to satisfy system performances, and adaptive control seems today an efficient strategy to study the stabilization and tracking of highly uncertain dynamical systems.
Since neural networks (NNs) have the advantages of inherent approximation capabilities and learning ability, they have been successfully implemented for identification and control of non-linear systems [1-10]. Especially, RNNs are suitable for dynamic mappings and lead to good control performance in the presence of unmodeled dynamics [10-12].
It is well known that FFN and RNN could be used as components in feedback systems [13]. The control system must satisfy three main conditions: boundedness of the NN weights, boundedness of the tracking error and stability of the global system under control. In an attempt to guarantee these criterions, a considerable research effort has concerned the design of neural networks control with high accurate tracking performances and strong robustness [14]. A major design technique has emerged with the use of the Lyapunov theory. The main advantage of this approach is that the parameter adaptation laws ensure the asymptotic stability of the closed-loop system.
The adaptive neural controllers can be classified according to three structures, such as, inverse model [15], direct [1,5,14] and indirect [9,10,13] control design. Neural control schemes can also be divided into “pure” neural controllers [1,11,13] and neural controllers combined with other conventional control strategies such as back stepping and sliding mode [5,14,16]. In that case, the role of neural networks is to approximate the nonlinear part of the input-output relation.
For multivariable nonlinear systems, due to the couplings among various inputs and outputs, the control problem is more complex and few results are available in the literature. In [8,9] the authors presented a stable adaptive control scheme for a multivariable nonlinear systems with a triangular structure using multilayer neural networks. The control design is based on integral type Lyapunov function and the block-triangular structure properties. These control schemes, however, cannot be extended to the general class of MIMO nonlinear systems.
The preceding works suffer from one or more of the following drawbacks: 1) the NNs used are linearly parameterised, whereas a non-linear model is necessary in order to control non-linear systems. 2) The system to be controlled is of a special known structure, (e.g., a traingular structure). Such results cannot be directly applied to an entirely unknown system. 3) The performances, for example stability and robustness, are locally guaranteed. 4) The model and/or the controller are fixed at the end of the training phase and the operational phase performances can be strongly degraded. It is often difficult to obtain the data which cover the whole range of the process excitation (problem of sufficient excitation).
In contrast to the above, the result presented in this paper avoids these drawbacks by establishing a stable adaptive control scheme based on the use of recurrent neural networks. In order to prove the industrial interest of the method for engineers, the application and validation of IDNC have been applied to robot manipulator which is a nonlinear system, multivariable with timevarying and/or inaccurately-known parameters. The controlled process is considered as a “black box” whose operating model is completely unknown. The main advantage of the proposed method is that models of the systems do not have to be known. Starting from zero values, weights, updating rates and time parameters of both adaptive instantaneous neural model and controller one, adapt themselves in order to track continuously the plant dynamics.
This paper is organized as follows. Section 2 describes IDNC structure, adaptation algorithm, stability and robustness conditions. Section 3 deals with the manipulator robot definition. In section 4 the experiment results are presented. Finally section 5 concerns our conclusions and perspectives.
2. Adaptive NN Control
The proposed control scheme is an Indirect Neural network Controller (IDNC) composed of two separate fully connected recurrent neural networks: the Neural Controller (NC) and the Adaptive instantaneous Monitoring Network (AMN) [13]. The aim of AMN is to provide an estimation of the process output(s) during a short time window in order to drive NC. The subscripts m and c are used to distinguish the AMN and NC respectively. The updating of NC and AMN is synchronous (Figure 1, the dash lines show the RTRL paths to update the parameters of AMN and NC). Discrete time is considered and for simplicity, let us refer to instant t = kΔT by using the integer k, with ΔT the sampling period.
Let us define NIN and NOUT respectively as the number of plant inputs and outputs and assume that NIN = NOUT, where IN and OUT represent the set of input and output indexes.
When the process is running, the neural networks continuously adapt. Comparison of the physical measurements with the neural network inputs and outputs is realised at each time. All the measured and manipulated
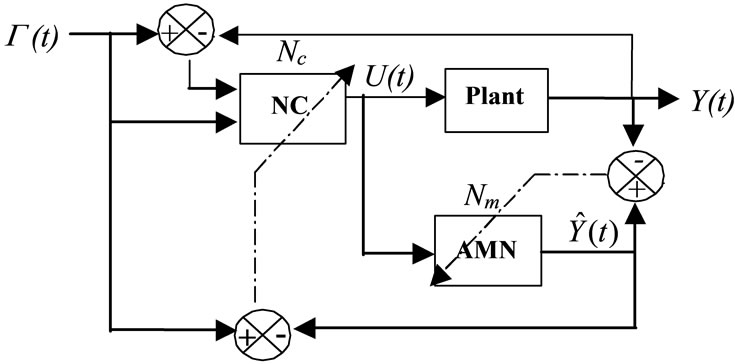
Figure 1. Structure of the indirect neural network control, the dimension of Y(t),  (t) and G(t) is NOUT, the dimension of U(t) is NIN.
(t) and G(t) is NOUT, the dimension of U(t) is NIN.
variables X correspond to physical signals (angular positions, spherical-coordinates, etc.) and have positive values constrained into an interval .
.
The activation function of the neurons are hyperbolic functions, therefore the network outputs evolve into the interval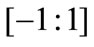 .
.
The algebraic expression of this transformation is given by:
 (1)
(1)
Let us notice that there is no pre or post-training phase but only an on-line updating of the weights, time parameters and adaptation parameters.
To avoid the problem of persistent excitation and to provide an instantaneous model that adapts itself when plant or environment changes, AMN parameters are updated in real time. Since adaptation continues as long as the controller drives the process (it is not our intention to memorize the dynamics of the controlled system). The idea is to compute an instantaneous behavioural model from input and output data of the plant. This instantaneous model is used to automatically update the controller parameters in order to track the process variations. The real time adaptation provides an efficient compensation of the unpredictable process disturbances and sensor.
The autonomous evolution of AMN and NC starts from zero values. It results in a compact structure with a small number of nodes (Nm = NIN + NOUT neurons for AMN and Nc = 2 × NOUT neurons for NC) [13,17]. The dynamics of Nm and Nc neurons are given according to “Equations (2) and (3)” respectively.
 (2)
(2)
 (3)
(3)
where B(k) = (Bi(k)) Î IRNm and D(k) = (Di(k)) Î IRNc are considered as constant during each sampling period with:
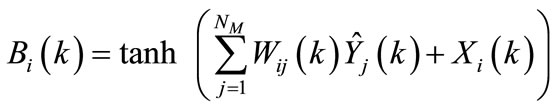 (4)
(4)
 (5)
(5)
 if
if  and
and  if
if 

Gi(k) corresponds to the ith plant desired output to be tracked. ŷi(k), Wij(k) (resp. Ui(k), fij(k)) and 1/t represent respectively the ith neuron state, weights value from jth to ith neuron and the adaptive time parameter of NC (resp. AMN).
The development of autonomous adaptation algorithm parameters are given by “Equations (6), (7) and (8)”.
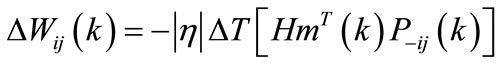 (6)
(6)
 (7)
(7)
 (8)
(8)
where  and
and .
.
The notation  indicates a vector of the 3D matrix P. The parameters |h| represent the learning rate of both neural networks.
indicates a vector of the 3D matrix P. The parameters |h| represent the learning rate of both neural networks. ,
,
 ,
,  and
and 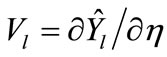 are the network sensitivity functions.
are the network sensitivity functions.
Stability and robustness properties of the closed loop system are important issues to be addressed. Indeed, small parameter uncertainties and external disturbances can have an unfavourable impact on performance as well as stability. In addition, the dynamic behaviour of the networks can lead to instability of the plant.
The application of the following theorems [11,17-20], guarantee the stability and robustness properties of the closed loop system.
Theorem 1
Let |h| be the adaptive updating rate of both the model and control networks, suppose the Lyapunov function is defined by:

Then the variation of the Lyapunov function could be expressed as , where the three parameters a, b and c depend on the process dynamics.
, where the three parameters a, b and c depend on the process dynamics.
The sufficient stability condition for the IDNC in the sense of Lyapunov should satisfy the following updating rate bounds:
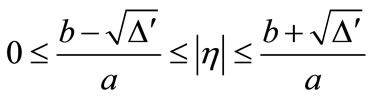 (9)
(9)
where  depends on the updating procedure and must be non-negative.
depends on the updating procedure and must be non-negative.
Theorem 2
Let |h| be the adaptive learning rate of both the monitoring and control networks. Suppose that the sensor noise quickly varies compared to the process dynamics. The IDNC compensates the sensor noise, if the following sufficient condition holds:
 (10)
(10)
where a is an arbitrary threshold depends on the tolerate noise ratio and  the usual Euclidean norm.
the usual Euclidean norm.
Theorem 3
A sufficient condition on the uncertainty parameters (DW, Dt) for robust stability is given by:
 (11)
(11)
where  is the infinite norm of a matrix and K a confidence band of uncertainties which depends on the nominal parameters of AMN.
is the infinite norm of a matrix and K a confidence band of uncertainties which depends on the nominal parameters of AMN.
Figure 2 sums up different conditions on the networks parameters that perform the robustness and the stability of the control system. Theorems 1 and 2 constrain explicitly the evolution of the adaptation parameter h and indirectly the evolution of other parameters. Theorem 3 describe robustness stability performance
3. Control Design for the Manipulator Robot
Our proposed control algorithm is applied on a medical robot designed for dental implantation (Figure 3) [21]. The robot is a semi-active mechanical device. It has a passive arm and a motorised wrist with three degrees of freedom that are not convergent. The base of the medical robot is passive, i.e. it is not motorised and can be manipulated by the surgeon in any direction.
The aim of the controller is to guide the surgeon so that it will respect the scheduled orientation.
The difficulty of the robot control lies in the calculation of the inverse model that connects the geometric variables to joint variables. Indeed, for a given direction of the robot end-effector, joint variables can be calculated by solving the inverse model equations which permits multiple solutions. According to the actual position of the actuators and the calculated joint variables, the controller must select the optimal solution which prevents large rotation of the actuators. The IDNC approximates both the direct and inverse model of the robot by

Figure 2. Updating including the different conditions in the network parameters space evolution.
AMN and NC. The IDNC parameters are adapted in real time in order to minimise a quadratic cost function. This cost function is defined according to the difference between the orientation of the “robot end-effector” vector and the orientation of the “patient” vector and also its variation. Maintain the same orientation between the two vectors are considered as the control objective.
The angular positions of both actuators are considered as plant inputs. The process outputs and desired ones of the “robot end effector” and “patient” vectors are given by the spherical-coordinates (θ and β) (Figure 4).
The nonlinear process is completely unknown for our algorithm which only needs the input and output data and does not require any knowledge about the process model. The autonomous evolution starts from zero initial conditions. It results in a compact structure: the NC has six neurons and the AMN has four neurons [20].
Figure 5 depicts the tracking performance and angular positions of both actuators obtained with our adaptation algorithm. It can be observed from (Figure 5(d)) that, after a short adaptation stage, due to |η| and |τ| parameters start from zero values, the proposed IDNC achieves good results (nmse = 3.2 e-004). This effect resulted in smoothing action of the learning rate stabilisation constraint, which assures that the closed loop system would