Analysis of Dynamics of Boundary Shape Perturbation of a Rotating Elastoplastic Radially Inhomogeneous Plane Circular Disk: Analytical Approach ()
1. Introduction
The failure of bearing capacity of a quickly rotating elastic disc [1-3] overloaded by centrifugal dilating forces is associated with the dynamics of its boundary shape perturbation [4]. After the disc takes up new balanced shape due to considerable growth of plastic zones [5] the instability [6] develops torrentially enough with the increase of rotation velocity [7]. This is stipulated by the response of the internal points to the disc contour reshaping and outrunning growth of variable radius of the perturbed elastoplastic boundary as compared with the variation of its current radius for a stable disc [8,9].
To study the stability loss and velocity dynamics of a rotating disc the perturbation method can be applied [10-12]. In the analysis of plane stress strain state this method was employed to obtain approximate critical values of the plastic zone dimensions and angular velocity of continuous homogeneous circular discs [13,14], ring-shaped discs [15] including those loaded along the contour by additional radial forces [16], stepped discs and some arbitrary profile discs [17] as well as simplest inhomogeneous discs. This proves efficiency of the analytical method of boundary shape perturbation (with the use of simplest numerical procedures at certain stage) which reduces essentially the amount of calculations and at the same time facilitates fruitful application of various numerical techniques [18-20] for stability and strength calculation of turbine and other massive discs.
Meanwhile, there is still an open problem of establishing by the small parameter method the relationship between the value of boundary shape perturbation, plastic zone radius and rotation velocity of unstable continuous inhomogeneous circular disc corresponding to the indicated state of perturbed elastoplastic boundary. This is the subject of our present investigation.
2. Statement of the Problem
We consider a disc D consisting of two homogeneous and isotropic plane discs D1 and D2. Continuous circular disc D1 possesses radius 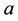 which coincides with the internal radius of the ring-shaped circular disc D2. The external radius of disc D2 equals to
which coincides with the internal radius of the ring-shaped circular disc D2. The external radius of disc D2 equals to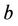 . Discs D1 and D2 made from different materials are rigidly connected into one disc D along the circumference
. Discs D1 and D2 made from different materials are rigidly connected into one disc D along the circumference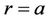 . We designate by
. We designate by 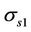 the material yield limit of disc D1,
the material yield limit of disc D1,  is the elasticity modulus,
is the elasticity modulus, 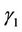 is the density and
is the density and 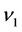 is the Poisson coefficient. The corresponding material parameters of disc D2 are designated by
is the Poisson coefficient. The corresponding material parameters of disc D2 are designated by ,
,  ,
,  and
and 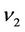 respectively. It is assumed that constant angular rotation velocity
respectively. It is assumed that constant angular rotation velocity  of disc D is higher than its critical velocity
of disc D is higher than its critical velocity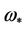 . This means the presence of perturbation of the initial contour circumference
. This means the presence of perturbation of the initial contour circumference , perturbation of the current radius of elastoplastic boundary
, perturbation of the current radius of elastoplastic boundary  and, in general, perturbation of stress strain state of the whole (unstable) disc.
and, in general, perturbation of stress strain state of the whole (unstable) disc.
We focus our attention on the self-balanced form of the stability loss of disc D which is little different from the circular form. The disc boundary equation up to the first order infinitesimal is presented in the form
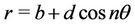 ,
, 
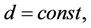
or
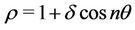 , (1)
, (1)
where  is a dimensionless current radius,
is a dimensionless current radius, 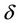 is a small parameter,
is a small parameter,  ,
, 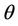 is a polar angle. On this basis, let us determine critical values
is a polar angle. On this basis, let us determine critical values  and
and  which accompany reaching of the above mentioned circumference
which accompany reaching of the above mentioned circumference  by the perturbed elastoplastic boundary in the elastic zone of disc D. The critical values corresponding to reaching of the disc edge by the elastoplastic boundary, i.e. its contact with curve (1), should be specially calculated. We recall that for solution of these problems it is necessary, first of all, to analytically establish the condition of contact of the elastoplastic boundary and a circumference of given radius, i.e. to construct characteristic equation with the parameter
by the perturbed elastoplastic boundary in the elastic zone of disc D. The critical values corresponding to reaching of the disc edge by the elastoplastic boundary, i.e. its contact with curve (1), should be specially calculated. We recall that for solution of these problems it is necessary, first of all, to analytically establish the condition of contact of the elastoplastic boundary and a circumference of given radius, i.e. to construct characteristic equation with the parameter 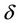 with respect to
with respect to  having solved first the system of linear equations
having solved first the system of linear equations





with respect to 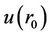 and arbitrary constants found in the expressions for stress and displacement components
and arbitrary constants found in the expressions for stress and displacement components ,
, 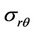 ,
,  and
and  determining perturbed stress strain state of the rotating disc D. The above mentioned linearized perturbations of the first order of smallness satisfy differential balance equations of plane problem and partial differential equations of relationship between stresses and displacements [1]. Unperturbed stress state (designated by the upper index 0) is determined by ordinary differential equations of quasistatic equilibrium and constraint equations in the elastic zone or by the yield Saint-Venant condition [5] in the plastic zone.
determining perturbed stress strain state of the rotating disc D. The above mentioned linearized perturbations of the first order of smallness satisfy differential balance equations of plane problem and partial differential equations of relationship between stresses and displacements [1]. Unperturbed stress state (designated by the upper index 0) is determined by ordinary differential equations of quasistatic equilibrium and constraint equations in the elastic zone or by the yield Saint-Venant condition [5] in the plastic zone.
In view of the instability development mechanism of the inhomogeneous disc under consideration the stated problem will be solved for each of the four cases: (a) D1peD2e (Figure 1(a)); (s2) D1pD2pe (Figure 1(b)); (b) D1eD2pe (Figure 1(c)); (c) D1peD2pe (Figure 1(d)).
3. Solution in the Case D1peD2e
In order to use boundary and conjugation conditions
 (2)
(2)
 (3)
(3)
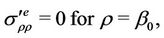 (4)
(4)
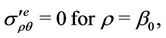 (5)
(5)
 (6)
(6)
for perturbations of the first order of smallness ,
, 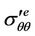 and
and  of radial, contact and tangential stresses related to the yield limit
of radial, contact and tangential stresses related to the yield limit 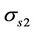 we recall that in D2e (Figure 1(a))
we recall that in D2e (Figure 1(a))
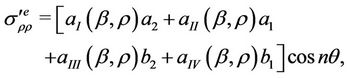

and in D1e

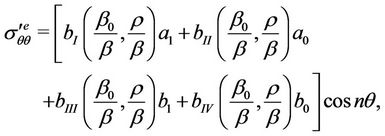

and, besides,

Here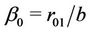 ,
, 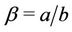 ,
, 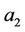 ,
, 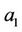 ,
, 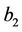 and
and  are indefinite coefficients and
are indefinite coefficients and  are the coefficients expressed via
are the coefficients expressed via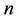 ,
, 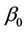 ,
, 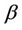 ,
,  ,
, 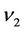 and
and ;
;
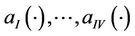 ,
,  ,
,  are known functions [16]. Moreover,
are known functions [16]. Moreover,
 (7)
(7)
where
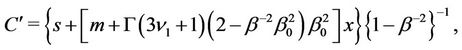
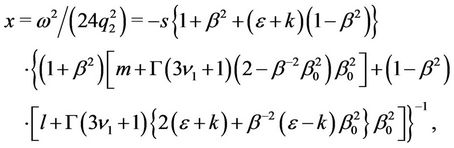

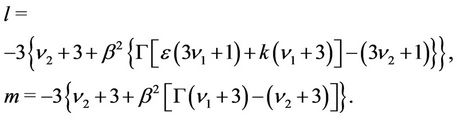
For  perturbation of the first order of smallness of the radial displacement related to
perturbation of the first order of smallness of the radial displacement related to 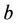 is known from (1)
is known from (1)

Therefore,

Conditions (2)-(6) in the extended form [16] are
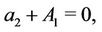
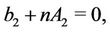


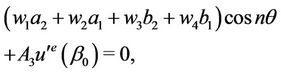
where


Hence,

where
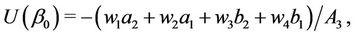
and, besides,

As a consequence, the characteristic equation with respect to the plastic zone radius corresponding to the moment of contact of the perturbed elastoplastic boundary and the mentioned circumference 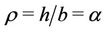 becomes
becomes
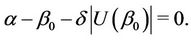 (8)
(8)
The critical value of angular velocity  corresponding to the critical value of radius of the plastic domain
corresponding to the critical value of radius of the plastic domain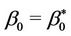 ,
, 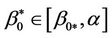 (
(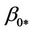 is a critical radius of the plastic zone D1p for which the disc loses its stability) is obtained in terms of (7).
is a critical radius of the plastic zone D1p for which the disc loses its stability) is obtained in terms of (7).
4. Solution in the Case D1pD2pe
Now, in contrast to Section 3, the elastic domain is homogeneous and represents zone D2e (Figure 1(b)), therefore [14,15]


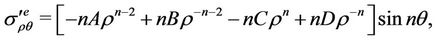
where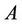 ,
,  ,
,  and
and  are indefinite coefficients. Correlations (7) are written as
are indefinite coefficients. Correlations (7) are written as
 (9)
(9)
where

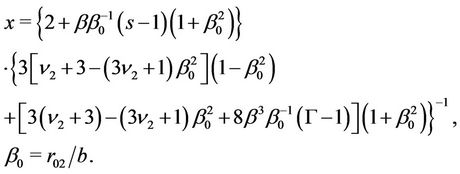
Therefore, the system of equations for determination of 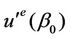 has the form
has the form
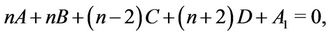
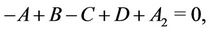
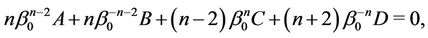
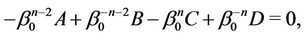

Hence,
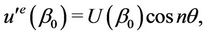
where
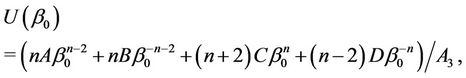
and, moreover,
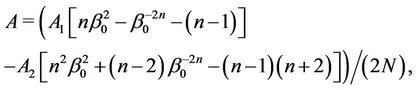
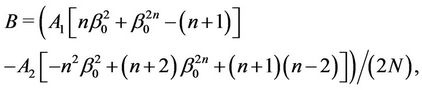
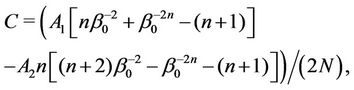
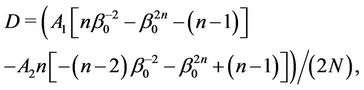
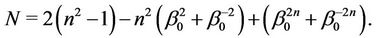
Thus, characteristic Equation (8) is constructed.
The characteristic equation with a parameter with respect to critical radius of the plastic domain which reached the external edge of the disc D reads [9]
 (10)
(10)
where 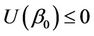 for
for .
.
5. Solution in the Case D1eD2pe
Having compared stress states (unperturbed and perturbed) of the disc D in cases (s1) and (b) (Figure 1(c)) of instability development we conclude about the necessity to preserve here all calculations of Section 4 having changed the expression for 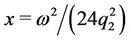
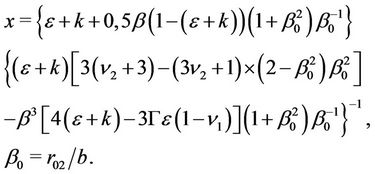
6. Solution in the Case D1peD2pe
In order to follow the perturbation dynamics of elastoplastic boundary between D2p and D2e (Figure 1(d)) we will take into account (see Section 4) the fact that
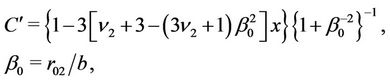

where



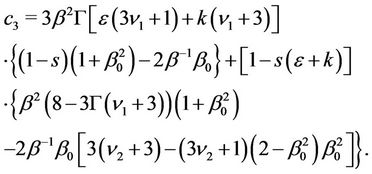
Similarly to Section 5 the rest of calculations including general form of characteristic Equations (8) and (10) coincide with the results presented in Section 4.
7. Examples and Concluding Remarks
For inhomogeneous disc with the parameters ,
, 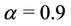 ,
,  ,
, 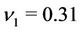 ,
, 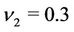 ,
, 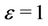 ,
, 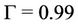 ,
,  and
and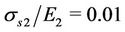 , which loses its stability according to case (a) for
, which loses its stability according to case (a) for 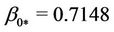 and
and 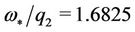 the values of critical radius
the values of critical radius  of plastic zone D1p and relative critical rotation velocity
of plastic zone D1p and relative critical rotation velocity 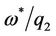 are presented in Table 1.
are presented in Table 1.
Table 2 presents characteristic critical values obtained in terms of solution of characteristic Equation (10) for the disc with parameters ,
, 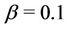 ,
, 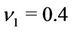 ,
, 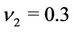 ,
,  ,
,  ,
,  and
and 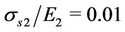 which loses its stability according to case (s2) for
which loses its stability according to case (s2) for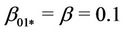 ,
,  and
and .
.
The same problem is solved for the disc with ,
,  ,
,  ,
,  ,
, 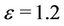 ,
, 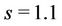 and
and  whose instability develops according to (b) (Table 3) for
whose instability develops according to (b) (Table 3) for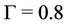 ,
, 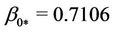 and
and 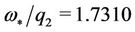 and according to (c) (Table 4) for
and according to (c) (Table 4) for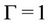 ,
, 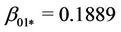 ,
, 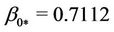 and
and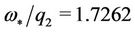 .
.
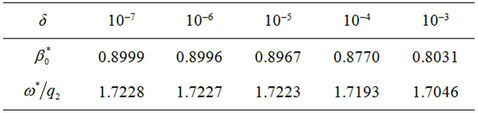
Table 1. Values of critical radius and relative critical velocity depending on δ.

Table 2. Values of critical radius and relative critical velocity depending on δ.

Table 3. Values of critical radius and relative critical velocity depending on δ.
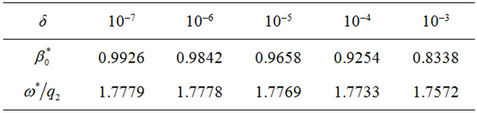
Table 4. Values of critical radius and relative critical velocity depending on δ.
The relationships established between the value of boundary shape perturbation, location and type of perturbed elastoplastic boundary and rotation velocity of unstable continuous circular disc allow qualitative and quantitative conclusions to be made about peculiarities of the disc super-high-speed dynamics. The application of the obtained results enables us to forecast the development of unstable state and to calculate possible loss of stability and failure of bearing capacity of rotating discs.
It should be noted that basic equations of stability theory of spatial deformable bodies derived by linearization of nonlinear equations contain terms specified via the components of unperturbed ground state. This causes some difficulties in the problem on loss of stability, since a loading parameter associated with the critical efforts enters the basic equations. Application of the approximated approach presented in the paper for stability investigation of spatial elastic bodies simplifies the problem because both the perturbations 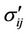 satisfy the initial balance equations and the loading parameter is introduced into boundary conditions on the perturbed initial surface of the body. The loading parameter is determined by essentially more simple characteristic equations.
satisfy the initial balance equations and the loading parameter is introduced into boundary conditions on the perturbed initial surface of the body. The loading parameter is determined by essentially more simple characteristic equations.