1. Introduction and Notation
We use [1] for terminology and notations not defined here and consider simple undirected graphs only. Let  be a graph. A proper edge-coloring of G is a function
be a graph. A proper edge-coloring of G is a function 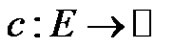 (
( is the set of non-negative integers) such that any two adjacent edges have distinct colors. If G is assigned such a coloring c, then we say that G is a properly edge-colored graph, or simply a properly colored graph. Let
is the set of non-negative integers) such that any two adjacent edges have distinct colors. If G is assigned such a coloring c, then we say that G is a properly edge-colored graph, or simply a properly colored graph. Let  denote the color of the edge
denote the color of the edge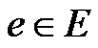 . For a subgraph H of G, let
. For a subgraph H of G, let
 .
.
A subgraph H of G is called rainbow if its edges have distinct colors. Recently rainbow subgraphs have received much attention, see the survey paper [2]. Here we are interested in rainbow matchings. The study of rainbow matchings began with the following conjectures.
Conjecture 1. (Ryser [3,4]) Every Latin square of odd order has a Latin transversal.
Conjecture 2. (Stein [5]) Every Latin square of order n has a partial Latin transversal of size at least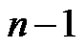 .
.
An equivalent statement is that every proper n-edgecoloring of the complete bipartite graph 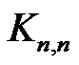 contains a rainbow matching of size
contains a rainbow matching of size  Moreover, if n is odd, there exists a rainbow perfect matching. Hatami and Shor [6] proved that there is always a partial Latin transversal (rainbow matching) of size at least
Moreover, if n is odd, there exists a rainbow perfect matching. Hatami and Shor [6] proved that there is always a partial Latin transversal (rainbow matching) of size at least .
.
Another topic related to rainbow matchings is orthogonal matchings of graphs. Let G be a graph on n vertices which is an edge disjoint union of m k-factors (i.e. k regular spanning subgraphs). We ask if there is a matching M of m edges with exactly one edge from each k-factor? Such a matching is called orthogonal because of applications in design theory. A matching M is suborthogonal if there is at most one edge from each k-factor. Alspach [7] posed the above problem in the case . Stong [8] proved that if
. Stong [8] proved that if , then there is a such orthogonal matching. For
, then there is a such orthogonal matching. For , the answer is yes, see [9]. In the same paper, Anstee and Caccetta proved the following theorem when
, the answer is yes, see [9]. In the same paper, Anstee and Caccetta proved the following theorem when .
.
Theorem 3. [9] Let G be an m-regular graph on n vertices. Then for any decomposition of  into m 1-factors
into m 1-factors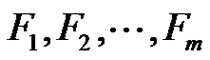 , there is a matching M of p edges, at most one edge from each 1-factor, with
, there is a matching M of p edges, at most one edge from each 1-factor, with

In any decomposition of 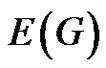 into m k-factors, we can construct an edge colored graph by giving each kfactor a color. Then a rainbow matching of G corresponds to a suborthogonal matching of G. In particular, when
into m k-factors, we can construct an edge colored graph by giving each kfactor a color. Then a rainbow matching of G corresponds to a suborthogonal matching of G. In particular, when , the edge colored graph obtained above is properly colored. So we can pose a more general problem: Let G be a properly colored graph of minimum degree
, the edge colored graph obtained above is properly colored. So we can pose a more general problem: Let G be a properly colored graph of minimum degree . Is there a rainbow matching of size
. Is there a rainbow matching of size ? Unfortunately, the answer is negative, see [10]. Moreover, if G is a properly colored complete graph, then G has no rainbow matching of size more than
? Unfortunately, the answer is negative, see [10]. Moreover, if G is a properly colored complete graph, then G has no rainbow matching of size more than . In addition, the following theorem was shown in [11].
. In addition, the following theorem was shown in [11].
Theorem 4. [8] Let G be a properly colored graph,  , and
, and . Then G contains a rainbow matching of size
. Then G contains a rainbow matching of size .
.
However, we believe that if the order of a properly colored graph G is much larger than its minimum degree , there should be a rainbow matching of size
, there should be a rainbow matching of size . In [10], we propose the following problem.
. In [10], we propose the following problem.
Problem 5. [10] Is there a function  such that for each properly colored graph G with
such that for each properly colored graph G with 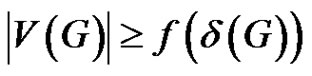 , G must contain a rainbow matching of size
, G must contain a rainbow matching of size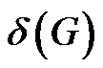 ?
?
Since when n is even, an  Latin square has no Latin transversal (perfect rainbow matching) (see [3]), if the function
Latin square has no Latin transversal (perfect rainbow matching) (see [3]), if the function  exists,
exists,  should be greater than 2n. Motivated by this problem, we prove the following results in [10].
should be greater than 2n. Motivated by this problem, we prove the following results in [10].
Theorem 6. [10] Let G be a properly colored graph and . Then G has a rainbow matching of size at least
. Then G has a rainbow matching of size at least .
.
Theorem 7. [10] Let G be a properly colored trianglefree graph. Then G has a rainbow matching of size at least .
.
In [12], Wang, Zhang and Liu proved that if then G has a rainbow matching of size
then G has a rainbow matching of size , which answers the above question in the affirmative. Eiemunsch et al. [13] improved this bound to
, which answers the above question in the affirmative. Eiemunsch et al. [13] improved this bound to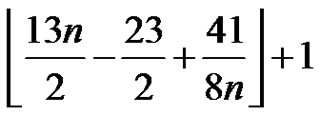 . Later, this bound was improved to
. Later, this bound was improved to  by Lo in [14].
by Lo in [14].
In this paper, we consider the rainbow matching of the properly colored bipartite graph, and prove the following result.
Theorem 8. Let G be a properly colored bipartite graph with bipartition  and
and . If
. If  , then G has a rainbow coloring of size at least
, then G has a rainbow coloring of size at least .
.
For more result about rainbow matchings under the color degree conditions, we refer to [15,16].
2. Proof of Theorem 8
Let . Without loss of generality, we assume that
. Without loss of generality, we assume that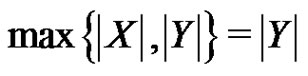 . Suppose that our conclusion is not true, we choose a maximum rainbow matching M. Let
. Suppose that our conclusion is not true, we choose a maximum rainbow matching M. Let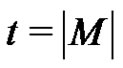 . Without loss of generality, we assume that
. Without loss of generality, we assume that
 .
.
Then  Let
Let  and
and  Put
Put  and
and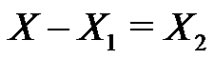 . Let
. Let  denote the vertices in X which are incident with
denote the vertices in X which are incident with  by three edges with new colors. Clearly,
by three edges with new colors. Clearly, . Otherwise, we can get a rainbow matching of size at least
. Otherwise, we can get a rainbow matching of size at least , which is a contradiction. Let
, which is a contradiction. Let  denote the vertices which are incident with the vertices in
denote the vertices which are incident with the vertices in 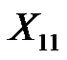 by the edges in M. We have the following claim.
by the edges in M. We have the following claim.
Claim 1.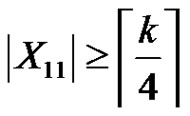 .
.
Proof. Let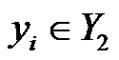 . If there is an edge
. If there is an edge  such that
such that , then
, then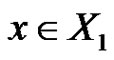 . Otherwise, there is a rainbow matching
. Otherwise, there is a rainbow matching  of size
of size , which is a contradiction. Let
, which is a contradiction. Let 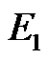 denote the edges which are incident with vertices in
denote the edges which are incident with vertices in  and have new colors. Since each vertex in
and have new colors. Since each vertex in  has degree at least
has degree at least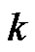 ,
,
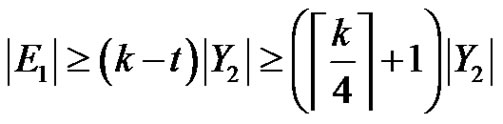 .
.
On the other hand, . So we have the following equality
. So we have the following equality
 .
.
Hence
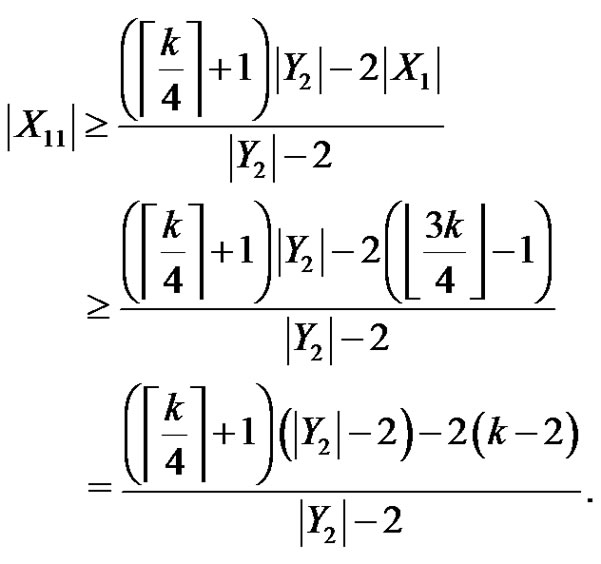
Since ,
,  , thus
, thus .
.
Without loss of generality, we assume that where
where . Let
. Let  denote the vertex which is incident with
denote the vertex which is incident with 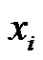 by an edge in M.
by an edge in M.
Claim 2. Let  be any vertex in
be any vertex in 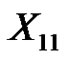 and
and  denote the vertex which is incident with
denote the vertex which is incident with 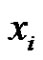 by an edge in M. If
by an edge in M. If 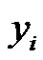 is incident with a vertex
is incident with a vertex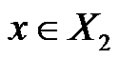 , then
, then  .
.
Proof. Suppose our conclusion does not hold. First, we know that 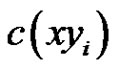 can not be a new color. Otherwise, since
can not be a new color. Otherwise, since 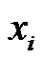 are incident with three edges having new colors, we can choose one edge (say e). Then we can get a new rainbow matching of size
are incident with three edges having new colors, we can choose one edge (say e). Then we can get a new rainbow matching of size  by adding
by adding  and deleting
and deleting . Thus we will get a contradiction. So we conclude that
. Thus we will get a contradiction. So we conclude that . Since G is properly colored,
. Since G is properly colored, . So without loss of generality, we assume that
. So without loss of generality, we assume that . Moreover, we assume that the edges with new colors are incident with
. Moreover, we assume that the edges with new colors are incident with 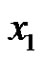 are
are 
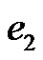 and
and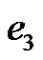 . Now we can choose
. Now we can choose  such that
such that  and
and  is not incident with y. Hence we have a new rainbow matching by adding
is not incident with y. Hence we have a new rainbow matching by adding  and deleting
and deleting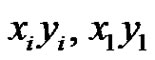 , which is a contradiction.
, which is a contradiction.
Claim 3. If there exists an edge  such that
such that  and
and , then
, then .
.
Proof. Suppose, to the contrary, . If
. If  is a new color, then clearly there exists a rainbow matching
is a new color, then clearly there exists a rainbow matching 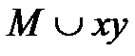 of size
of size . So we assume that
. So we assume that . Without loss of generality, we assume that
. Without loss of generality, we assume that . We can also choose one edge e incident with
. We can also choose one edge e incident with  such that e is not incident with y and
such that e is not incident with y and 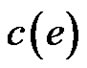 is a new color. Then we can also obtain a rainbow matching by adding
is a new color. Then we can also obtain a rainbow matching by adding  and deleting
and deleting , which is a contradiction. This completes the proof of Claim 3.
, which is a contradiction. This completes the proof of Claim 3.
Let xy be an edge such that 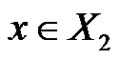 and
and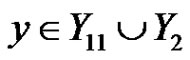 . By Claim 2 and Claim 3,
. By Claim 2 and Claim 3, . Let
. Let 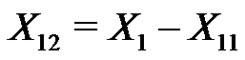 and
and  . Since
. Since ,
, .
.
On the other hand,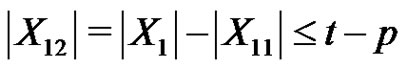 . Hence
. Hence  . That is
. That is , which contradicts with
, which contradicts with . This completes the whole proof.
. This completes the whole proof.
3. Acknowledgements
We would like to thank the referee for the careful review and the valuable comments. This research was supported by NSFC Grants (61070230, 11101243), IIFSDU (2009 hw001), RFDP (20100131120017) and SRF for ROCS.