Maximum Ratio Combining Precoding for Multi-Antenna Relay Systems ()
This paper addresses the design of practical communication strategies for multi-antenna amplify-and-forward and decode-and-forward relay systems. We show that simple linear techniques at the source and destination in conjunction with maximum ratio combining can provide an optimal transmission strategy in terms of received SNR without imposing a huge computational load over the relay node(s). Besides, the structures of precoding matrices are very similar at the source and relay nodes, which reduce the complexity as all nodes can play the role of source and relay nodes without changing their transmission structure. Numerical results show that the proposed transmission and reception techniques can improve the received SNR, and hence enhance the ergodic capacity.
1. Introduction
Relay networking [1-5] is one of the frameworks in which the concept of cooperation [6] becomes meaningful. In these systems, a source node tries to send its corresponding information to the destination node with the help of one or a number of relay node(s). Cooperative relaying targets additional diversity and coding gain and provides additional level of reliability, particularly when the direct source-destination link has poor quality.
Two natural questions in the context of relay networks are the problems of transmission and reception strategies. Mainly, how the source and relay node(s) should send the information to the destination node and how the destination should optimally combine the source information with replicate version(s) of information from relay node(s). Obviously, one cannot answer to these two questions separately. In other words, transmission and reception strategies should be jointly optimized.
A major practical issue to be addressed in the design of transmission and reception schemes in relay networks is complexity. Unlike point-to-point transmission schemes in which transmitter and receiver are responsible for the recovery of their own information, in the relay systems, other parts of the network are also engaged in the communications. Hence, it is very desirable that the communication strategy imposes minimum level of computational loads on the relay nodes. This point becomes one of the constraints that should be taken into account in the design of strategies for relay systems.
Two popular strategies can be considered for transmission in relay networks: amplify-and-forward (AF), in which a relay node does not decode the received signal but forwards it to the destination with a specific weight (e.g., [5,7-10]), and decode-and-forward (DF), in which a relay node decodes the received signal from the source and retransmits a decoded version of the signal to the destination (e.g., [11,12]). In this paper, we develop practical transmission and reception for both cases. In addition, throughout this paper, we assume that all terminals (nodes) operate in a half-duplex mode.
While there is a vigorous body of work on the relay systems in which each individual terminal is equipped with single antenna, the case of multi-antenna nodes has not been studied extensively. In [13], it was shown that the relay systems with MIMO capability offer a promising capacity and this capacity scales linearly with the number of antennas at source/destination and logarithmically with the number of relay nodes or antennas. For a similar case, a cooperative beamforming approach that can achieve the capacity of the network in the limit of large number of relay nodes was proposed in [14]. Another interesting setup can be found in [15] where the authors elaborate the effect of relay-assisted transmission on the capacity of rank-deficient MIMO systems.
While all the above results are attractive from a theoretical point of view, the need for practical transmission and reception schemes that can practically realize the ability of multi-antenna relay networks in providing higher capacity and performance compared to that of systems with single-antenna terminals is still pronounced. In [16], three signaling strategies for multi-antenna relay systems are discussed and compared. An optimal hybrid relaying strategy based on a combination of filtering and AF protocol was derived and can outperform AF relaying, especially when Channel State Information (CSI) is available at the relay node. In [17], an AF relaying structure that maximizes the capacity when there is no direct link between source and destination nodes has been introduced. The authors, however, mentioned that their analysis is intractable when there is a direct link between source and destination nodes.
The scarcity of studies on the design of communication schemes for multi-antenna relay systems in the literature is the main motivation of this study. More specifically, throughout this paper, we assume the source, destination and relay nodes are all equipped with multiple antennas. Our goal is to find optimal transmission and reception schemes for this setup while avoiding a huge complexity especially at the relay node. We show that a maximum ratio combining scheme at the receiver in conjunction with suitable linear precoding techniques at transmit and relay node can lead us to this end. Our study shows that the proposed scheme is optimal in terms of received SNR (and capacity) while maintaining an acceptable computational load at all nodes. In addition, the technique can be applied to both AF and DF protocols with small modifications. This feature can facilitate switching between two protocols whenever necessary. On the other hand, structures of source and relay nodes are identical, and, hence, enable a node to play the role of the source or relay in different time instants without the need of additional software or hardware overhead.
We further show that a Generalized Maximum Ratio Combiner (GMRC) at the destination is optimum for both AF and DF protocols in terms of SNR. Furthermore, for DF protocol, the precoders at the source and relay nodes should send the information in the direction of the eigenvectors corresponding to the strongest eigenvalues of the channel matrices. While it is straightforward to derive the precoding structure in the case of DF protocol, the case of AF cannot be elaborated easily. We instead propose a relay selection scheme that can result in the best possible received SNR.
The rest of the paper is organized as follows. In Section 2, we present the system model of the multi-antenna relay network. In Section 3, maximum ratio combining schemes for different scenarios such as point-to-point MIMO, multipoint-to-point system, AF and DF relaying are studied. Section 4 is allocated to the precoder design for transmit and relay nodes and in Section 5, numerical results are presented. Conclusions are given in Section 6.
2. System Model
We consider a relay system composed of one M-antenna source (transmit) node, one L-antenna relay node and one N-antenna destination (receive) node, operating in a half-duplex mode. For simplicity in notations, in the following analysis, we assume L = M and single-symbol transmission, i.e., at a specific time instant, the source tends to transmit a symbol x of a pre-determined code book (or constellation) to the destination1. It applies a precoding vector w1 of size M × 1 to this symbol and sends it to both the destination and relay nodes. In the next time slot, based on the specific protocol (AF or DF), the relay node multiplies the received symbol by another precoding vector w2 of the same size and resends this precoded version to the destination. Destination then combines the two received signals based on a maximum-ratio-combining strategy.
The received signal in the first time slot can be written as:
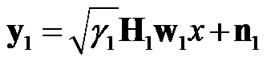 (1)
(1)
where H1 is the N × M forward channel matrix with normalized circularly symmetric Gaussian random entries, γ1 is its corresponding SNR, y1 and n1 are the received and white Gaussian noise vectors of size N×1, respectively. In the second time slot, the received signal is:
 (2)
(2)
where  is either a detected version of x at relay node for DF or
is either a detected version of x at relay node for DF or  for AF scenario. G is the source-relay M × M channel matrix, n is the M × 1 noise vector at relay and
for AF scenario. G is the source-relay M × M channel matrix, n is the M × 1 noise vector at relay and  is its corresponding SNR. H2, γ2, y2 and n2 are defined similar to their counterparts in (1). The destination combines these two signals using two weight vectors
is its corresponding SNR. H2, γ2, y2 and n2 are defined similar to their counterparts in (1). The destination combines these two signals using two weight vectors  and
and  to construct the received signal
to construct the received signal
 (3)
(3)
The decision is made on y to detect the transmit symbol x. Our goal is to find two precoding (w1 and w2) and two weight vectors ( and
and ) such that the received SNR is maximized. For limited transmit power, w1 and w2 are assumed to be
) such that the received SNR is maximized. For limited transmit power, w1 and w2 are assumed to be
 (4)
(4)
Maximizing SNR will minimize the probability of wrong decision over x. Also, we show that maximizing SNR in this scenario is equivalent to maximizing the instantaneous mutual information and ultimately the system capacity.
3. Generalized Maximum Ratio Combining
3.1. DF Relay-Assisted MIMO System
We first start consider a point-to-point MIMO system with M transmit antennas and N receive antennas in Figure 1(a). The transmitted symbol x is precoded at transmitter by precoder w and the received vector is combined using vector 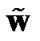 at the receiver. Therefore, the system model can be written as:
at the receiver. Therefore, the system model can be written as:
 (5)
(5)
where H, n and  are similar to H1 and n1 in (1), and the corresponding received SNR is
are similar to H1 and n1 in (1), and the corresponding received SNR is

It is well known that one can select 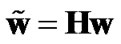 to achieve the maximum
to achieve the maximum  and maximum mutual information between x and
and maximum mutual information between x and ,
,
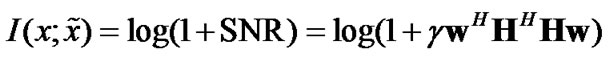 .
.
Now let consider the case when two transmitters send the same information to a receiver but in different time instants as shown in Figure 1(b). Both transmitters are equipped with M antennas while the receiver has N antennas. This case also corresponds to an ideal DF scenario when the relay node can always correctly decode the source information. The system model is the same as (1) and (2) except that  is replaced by x in (2). Combining (1), (2) and (3), one can write an equivalent compound system equation for the above scenario as
is replaced by x in (2). Combining (1), (2) and (3), one can write an equivalent compound system equation for the above scenario as
 (6)
(6)
This is clearly a MIMO system with 2M transmit antennas and 2N receive antennas, and the generalized maximum ratio combining (GMRC) scheme for such a system is
 ,
,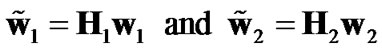 (7)
(7)
where
Note that there is a fundamental difference between MRC and GMRC as MRC just considers combining in space domain over elements of receive antennas while GMRC includes combining over both space and time.
In a general DF scenario, the received signal after combining becomes
 (8)
(8)
where x′ denotes the symbol decoded and re-transmitted by the relay, i.e., x′ = x for correct detection and x′ ≠ x for erroneous detection. Let α denote the probability of erroneous detection at the relay. The optimum combining vectors for DF transmission can be written as:
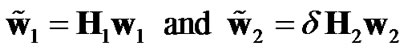 (9)
(9)
where the coefficient δ can be estimated from α. Consider an approximation by assuming that x′ = -x for an erroneous detection at the relay. Note that this consideration is exact for binary transmission. For a general M-ary signaling scheme, this assumption represents a pessimistic consideration. Under this assumption, the SNR’s corresponding to the cases of correct and erroneous detection at the relay are respectively,
 (10)
(10)
where

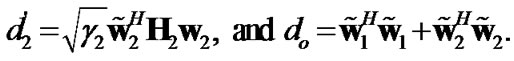
The average received SNR can then be written as (11).
From (11) and considering a system equation similar to (6) and (7), one can find the corresponding equivalent system equation for this general DF scenario as (12).
 (11)
(11)
 (12)
(12)
where H is the channel matrix of the equivalent MIMO system and can be approximated as:
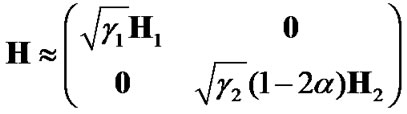
 (a)
(a)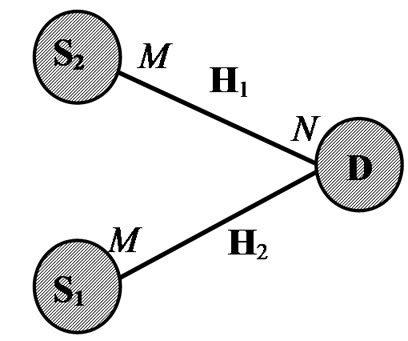 (b)
(b) 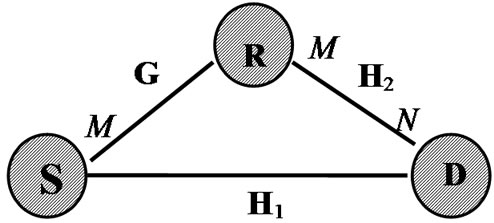 (c)
(c)
Figure 1: Diagrams of different transmission systems: (a) point-to-point MIMO; (b) multipoint-to-point MIMO; (c) relay-assisted MIMO.
In other words, the coefficient δ can be approximated as  when α is small. Note that one can use other estimations to find δ or the optimum weight ad-hoc. In general, the idea is to reduce the weight of the signal in the second transmit interval as it may contain error and degrade the total received SNR at the destination.
when α is small. Note that one can use other estimations to find δ or the optimum weight ad-hoc. In general, the idea is to reduce the weight of the signal in the second transmit interval as it may contain error and degrade the total received SNR at the destination.
3.2. AF Relay-Assisted MIMO System
The difficulty with this scenario is that the noise in the second time slot is no longer white. In other word, based on (1) and (2), the system equation in this case can be rewritten as:

 (13)
(13)
The difference between the AF and DF protocols is that W2 is the M × M precoding matrix (instead of vector) at the relay node, and the noise in the second time interval is no longer white. Assuming n and n2 are uncorrelated, the autocorrelation function of the noise in the second time interval can be written as:

 (14)
(14)
where IM denotes identity matrix of size M. Applying an eigenvalue decomposition over Λ, one can write Λ = UDUH where U and D are N × N unitary and diagonal matrices, respectively.
Defining the pre-whitening filter as  and applying it to the received signal in the second time-slot will make the output noise white. With that, one can apply (8) directly to derive the structure of combining vectors. The system model can be considered as (12) with:
and applying it to the received signal in the second time-slot will make the output noise white. With that, one can apply (8) directly to derive the structure of combining vectors. The system model can be considered as (12) with:
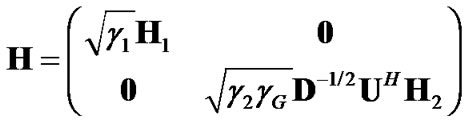
Now from (13), the optimum combining vectors for an AF relay-assisted MIMO system can be written as:
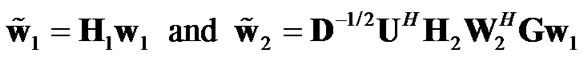 (15)
(15)
In other words, the optimum weight vector in the second time interval is a combination of an MRC vector and a pre-whitening filter. By applying pre-whitening filter, the output noise will be white and therefore one can apply the combining weight vectors in (15) to maximize the SNR, the instantaneous mutual information and ultimately the system capacity.
4. Precoding for Relay-Assisted MIMO Systems
Our goal here is to investigate the design of precoding vectors, w1 and w2, in (1) and (2). We start with pointto-point MIMO transmission and then generalize the results to the case of relay-assisted MIMO systems.
Recall that, after applying MRC weight vector, (6) yields . To maximize this SNR subject to power constraint over w, similar to (4), one should take w in the direction of the eigenvector of Hermitian matrix HHH associated with λmax where λmax is the largest eigenvalue of HHH. In other words, under the total transmit power constraint at source, the optimum precoding vector that maximizes the SNR of an MRC-based MIMO system can be written as
. To maximize this SNR subject to power constraint over w, similar to (4), one should take w in the direction of the eigenvector of Hermitian matrix HHH associated with λmax where λmax is the largest eigenvalue of HHH. In other words, under the total transmit power constraint at source, the optimum precoding vector that maximizes the SNR of an MRC-based MIMO system can be written as
 (16)
(16)
where umax stands for the eigenvector of H corresponding the maximum eigenvalue. With this precoding vector and considering the receive combining vector of , the receive SNR of the system can be written as
, the receive SNR of the system can be written as . From (8), (9) and (16), it can be shown that under the total transmit power constraints at source and relay nodes, for a multipoint-to-point MIMO system with GMRC combining vectors at receiver, the optimum precoding vectors are:
. From (8), (9) and (16), it can be shown that under the total transmit power constraints at source and relay nodes, for a multipoint-to-point MIMO system with GMRC combining vectors at receiver, the optimum precoding vectors are:
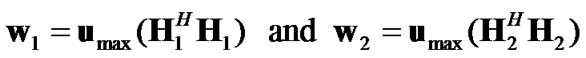 (17)
(17)
The same conclusion is also valid for the case of DF protocol for relay-assisted MIMO systems.
Now, we are ready to revisit the problem of AF protocol. The difficulty with this case is that the optimization of precoding matrix at the relay node, W2, is not independent of the optimization of precoding vector at the source node, w1. This is because the received SNR equation resulted in the second transmit interval is
 (18)
(18)
and, therefore, is a function of both w1 and W2. Note that (18) comes from applying (15) to calculate the SNR in (6). Although direct maximization of (18) for W2 would be difficult, one can make a clever guess that if we select W2 such that it maximizes SNR over the source-relay link, G, this can ultimately result in the maximization of the SNR in (18) over the entire link from source to destination. Therefore, assume that W2 can be written as
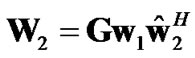 (19)
(19)
where Gw1 is responsible for maximizing the SNR at relay node while  is an independent vector reserved for further optimization of precoding matrix at the relay node. Moreover, for maximizing the SNR over the relay-destination link, using (16), it can be shown that
is an independent vector reserved for further optimization of precoding matrix at the relay node. Moreover, for maximizing the SNR over the relay-destination link, using (16), it can be shown that
 (20)
(20)
Now, w1, the precoding vector at the source node is the only remaining parameter to be selected. However, w1 affects the received SNR from both direct and relayed links. Therefore, to optimize w1, the SNR equations similar to (10) should be considered, which makes the optimization problem very difficult if not impossible to solve. To resolve this problem, we focus on each of the transmit intervals, separately. Since in a communication system, there are usually a number of available relay terminals (rather than just one), we, ultimately, propose the use of relay selection approach to maximize the overall SNR of the system.
Consider the received SNR in the first transmit interval:

Based on (16), SNR1 is maximized if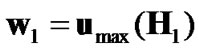 . On the other hand, in the second transmit interval, by substituting W2 of (19) into (18), it turns out that the source precoding vector will be responsible for the source-relay portion of the SNR. Therefore, to maximize this portion, one should select
. On the other hand, in the second transmit interval, by substituting W2 of (19) into (18), it turns out that the source precoding vector will be responsible for the source-relay portion of the SNR. Therefore, to maximize this portion, one should select . These two equations for w1 are definitely in contrast with each other. The best scenario is that
. These two equations for w1 are definitely in contrast with each other. The best scenario is that . In this case, based on (16), the overall receive SNR of the system can be written as:
. In this case, based on (16), the overall receive SNR of the system can be written as:
 (21)
(21)
Now, let assume that  but there are K available relay nodes in the system. The best relay should be selected such that the overall receive SNR is maximized. The performance degradation appears as a factor of
but there are K available relay nodes in the system. The best relay should be selected such that the overall receive SNR is maximized. The performance degradation appears as a factor of 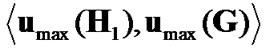 in the SNR equation. Two following extreme cases can be considered.
in the SNR equation. Two following extreme cases can be considered.
In the first case when the source-destination link is very strong (i.e., asymptotic case of ), one should choose the precoding vector in the direction of
), one should choose the precoding vector in the direction of . Therefore, the SNR loss as compared to the optimum case in (21), is due to the eigen-mismatch in the second transmit interval and the overall SNR can be expressed as:
. Therefore, the SNR loss as compared to the optimum case in (21), is due to the eigen-mismatch in the second transmit interval and the overall SNR can be expressed as:
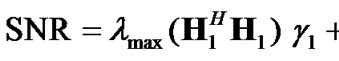
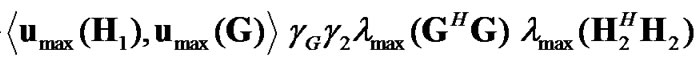 (22)
(22)
In the second case when the relay links are much stronger compared to the direct link (i.e., asymptotic case of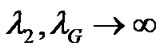 ), the natural selection is the source precoding vector in the direction of
), the natural selection is the source precoding vector in the direction of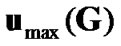 . In this case, the SNR loss is due to the eigen-mismatch in the first transmit interval. The overall received SNR can also be written as:
. In this case, the SNR loss is due to the eigen-mismatch in the first transmit interval. The overall received SNR can also be written as:

 (23)
(23)
Based on (22) and (23), amongst all K candidate relay nodes, the best relay node can be selected as

if the source-destination link is stronger than the sourcerelay and relay-destination links, or


if the source-relay and relay-destination links are stronger than the source-destination link. < , > stands for inner product. This selection maximizes the SNR of the relay-assisted AF system with high probability. In other words, the best relay is the one with strong source-relay and relay-destination links, i.e., large 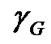 and
and , and when the eigenvector corresponding to the maximum eigenvalue of source-relay link matrix is the closest to
, and when the eigenvector corresponding to the maximum eigenvalue of source-relay link matrix is the closest to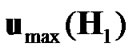 .
.
5. Numerical Results
We study the performance of the proposed MRC-based precoding technique by means of simulation. We consider all source, relay and destination nodes are equipped with two antennas, i.e., M = N = 2. We investigate the received SNR and average mutual information for these systems.
Figure 2 shows the received SNR for different setups in Figure 1. For the sake of comparison, we also show the performance of the precoder based on equal gain combining in point-to-point MIMO transmission. First, we observe that MRC-based precoding (case A) outperforms precoding with equal gain combining in terms of received SNR by about 3 dB. On the other hand, in the case of multipoint-to-point transmission (case B), precoding based on MRC can provide an additional gain as compared to the case of point-to-point transmission. This is mainly due to the availability of an additional path between the second transmit and receive nodes, which provides a higher average SNR at the receiver (especially when the link from first transmitter to receive node is poor). Finally, we see that the relay-assisted amplifyand-forward precoding system (case C) provides a received SNR comparable to that of an ideal multipoint-to-point system. The slight decrease in the received SNR is due to the noise accumulation in the relay node. The same conclusion is also valid for the case of a decode-and-forward system as there is a decrease in the received SNR due to the probability of wrong decision at the relay node.
Figure 3 also shows that the average mutual informa-