1. Introduction
Cyclic codes are a very important class of codes, they were studied for over fifty years. After the discovery that certain good nonlinear binary codes can be constructed from cyclic codes over Z4 via the Gray map, codes over finite rings have received much more attention. In particular, constacyclic codes over finite rings have been a topic of study. For example, Wolfmann [1] studied negacyclic codes over Z4 of odd length and gave some important results about such negacyclic codes. Tapia-recillas and Vega generalized these results to the setting of codes over  in [2]. More generally, the structure of negacyclic codes of length n over a finite chain ring R such that the length n is not divisible by the character p of the residue field
in [2]. More generally, the structure of negacyclic codes of length n over a finite chain ring R such that the length n is not divisible by the character p of the residue field  was obtained by Dinh and Lόpez-Permouth in [3]. The situation when the code length n is divisible by the characteristic p of residue field of R yields the so-called repeated root codes. Dinh studied the structure of
was obtained by Dinh and Lόpez-Permouth in [3]. The situation when the code length n is divisible by the characteristic p of residue field of R yields the so-called repeated root codes. Dinh studied the structure of  -constacyclic codes of length
-constacyclic codes of length  over
over  [4] where
[4] where  is any unit of
is any unit of  with form 4k − 1, and established the Hamming, homogenous, Lee and Euclidean distances of all such constacyclic codes. Recently, linear codes over the ring F2 + uF2 + vF2 + uvF2 have been considered by Yildiz and Karadeniz in [5], where some good binary codes have been obtained as the images under two Gray maps. Some results about cyclic codes over F2 + vF2 and Fp + vFp
with form 4k − 1, and established the Hamming, homogenous, Lee and Euclidean distances of all such constacyclic codes. Recently, linear codes over the ring F2 + uF2 + vF2 + uvF2 have been considered by Yildiz and Karadeniz in [5], where some good binary codes have been obtained as the images under two Gray maps. Some results about cyclic codes over F2 + vF2 and Fp + vFp
were given by Zhu et al. in [6] and [7] respectively, where it is shown that cyclic codes over the ring are principally generated. As these two rings are not finite chain rings, some techniques used in the mentioned papers are different from those in the previous papers. It seems to be more difficult to deal with codes over these rings. In this paper, we investigate (1 + 2v)-constacyclic codes over R + vR of length n (n is relatively prime to p, p is the character of the field , where R is a finite chain ring with maximal ideal
, where R is a finite chain ring with maximal ideal  and nilpotency index e, and
and nilpotency index e, and  = −v. We define a Gray map from R + vR to
= −v. We define a Gray map from R + vR to  and prove that the Gray map image of (1 + 2v)-constacyclic codes over R + vR of length n is a distance invariant linear cyclic codes of length 2n over R. The generator polynomials of this kind of codes of length n are determined and their dual codes are also discussed. We also prove that this class of constacyclic codes over the ring is principally generated.
and prove that the Gray map image of (1 + 2v)-constacyclic codes over R + vR of length n is a distance invariant linear cyclic codes of length 2n over R. The generator polynomials of this kind of codes of length n are determined and their dual codes are also discussed. We also prove that this class of constacyclic codes over the ring is principally generated.
2. Basic Concepts
In this section, we will review some fundamental backgrounds used in this paper. We assume the reader is familiar with standard terms from ring theory, as found in [8]. Let R be a finite commutative ring with identity. A code over R of length N is a nonempty subset of RN, and a code is linear over R of length N if it is an R-submoodule of RN. For some fixed unit μ of R, the μ-constacyclic shift 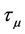 on RN is the shift
on RN is the shift 
 and a linear code C of length N over R is μ-constacyclic if the code is invariant under the μ-constacyclic shift
and a linear code C of length N over R is μ-constacyclic if the code is invariant under the μ-constacyclic shift . Note that the R-module
. Note that the R-module  is isomorphic to the R-module
is isomorphic to the R-module . We identify a codeword
. We identify a codeword  with its polynomial representation
with its polynomial representation . Then
. Then  corresponds to the μ-constacyclic shift of
corresponds to the μ-constacyclic shift of  in the ring
in the ring . Thus μ-constacyclic codes of length N over R can be identified as ideals in the ring
. Thus μ-constacyclic codes of length N over R can be identified as ideals in the ring . A code C is said to be cyclic if
. A code C is said to be cyclic if , negacyclic if
, negacyclic if , μ-constacyclic if
, μ-constacyclic if  respectively. Let R be a finite chain ring with maximal ideal
respectively. Let R be a finite chain ring with maximal ideal , e be the nilpotency index of
, e be the nilpotency index of , where p is the characteristic of the residue field
, where p is the characteristic of the residue field . In this section, we assume n to be a positive integer which is not divisible by p; that implies n is not divisible by the characteristic of the residue field
. In this section, we assume n to be a positive integer which is not divisible by p; that implies n is not divisible by the characteristic of the residue field , so that
, so that  is square free in
is square free in . Therefore,
. Therefore,  has a unique decomposition as a product of basic irreducible pairwise coprime polynomials in
has a unique decomposition as a product of basic irreducible pairwise coprime polynomials in . Customarily, for a polynomial f of degree k, it’s reciprocal polynomial
. Customarily, for a polynomial f of degree k, it’s reciprocal polynomial  will be denoted by
will be denoted by . Thus, for example, if
. Thus, for example, if , then
, then  . Moreover, if
. Moreover, if  is a factor of
is a factor of , we denote
, we denote , if
, if  is a factor of
is a factor of , we denote
, we denote , if
, if  is a factor of
is a factor of , we denote
, we denote . Obviously, we have
. Obviously, we have ,
,  .
.
The next six lemmas are well known, proof of them can be found in [4].
Lemma 2.1. Let C be a cyclic code of length n over a finite chain ring R (R has maximal ideal  and e is the nilpotency of
and e is the nilpotency of ). Then there exists a unique family of pairwise coprime monic polynomials
). Then there exists a unique family of pairwise coprime monic polynomials 
 in
in  such that
such that

and .
.
Moreover .
.
Lemma 2.2. Let C be a cyclic code of length n with notation as in Lemma 2.1, and 
 . Then
. Then  is a generating polynomial of C, i.e., C =
is a generating polynomial of C, i.e., C = .
.
Lemma 2.3. Let C be a cyclic code over R with
 where
where  as in Lemma 2.1and
as in Lemma 2.1and , then
, then

and .
.
Lemma 2.4. Let  be a negacyclic code of length over a finite chain ring R (R has maximal ideal
be a negacyclic code of length over a finite chain ring R (R has maximal ideal  and e is the nilpotency of λ). Then there exists a unique family of pairwise coprime monic polynomials
and e is the nilpotency of λ). Then there exists a unique family of pairwise coprime monic polynomials 
 in
in  such that
such that

and .
.
Moreover .
.
Lemma 2.5. Let C be a negacyclic code of length n with notations as in Lemma 2.6, and
 Then
Then 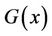 is a generating polynomial of C, i.e.,
is a generating polynomial of C, i.e., .
.
Lemma 2.6. Let C be a negacyclic code over R with

where  as in Lemma 2.6 and
as in Lemma 2.6 and , then
, then

and .
.
3. Graymap
Let  be the commutative ring
be the commutative ring  with
with . This ring is a kind of commutative Frobenius ring with two coprime ideals
. This ring is a kind of commutative Frobenius ring with two coprime ideals  and
and . Obviously, both
. Obviously, both  and
and  is isomorphic to R. By the Chinese Remainder Theorem, we have
is isomorphic to R. By the Chinese Remainder Theorem, we have .
.
In the rest of this paper, we denote R + vR by , where R is a finite chain ring with maximal ideal
, where R is a finite chain ring with maximal ideal , the nilpotency index of
, the nilpotency index of  is e, the character of the residue field
is e, the character of the residue field  is p, a prime odd.
is p, a prime odd.
We first give the definition of the Gray map on R. Let c = a + bv be an element in R, where . The Gray map
. The Gray map  is given by
is given by  where
where .
.
Lemma 3.1. The Gray map is bijection. If 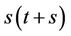 is a unit in R.
is a unit in R.
Proof. Since  is a unit in R, we can define a map
is a unit in R, we can define a map  by
by
 then for any
then for any , we have
, we have

This means that the  can be recovered from
can be recovered from  by the map
by the map , hence the Gray map
, hence the Gray map  is bijection.
is bijection.
The Gray map can be extended to  in a natural way:
in a natural way: 
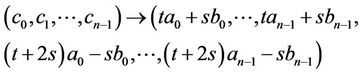
It is obvious that for any , we have
, we have  which means the Gray map
which means the Gray map  is R-linear.
is R-linear.
Lemma 3.2. Let  denote the
denote the  -constacyclic shift of
-constacyclic shift of  and
and  denote the cyclic shift of
denote the cyclic shift of . Let
. Let  be the Gray map of
be the Gray map of , then
, then .
.
Proof. Let , where
, where  with
with  for
for . From the definition of the Gray map, we have
. From the definition of the Gray map, we have

hence,

On the other hand,

We can deduce that

Therefore, .
.
Theorem 3.1. A linear code  of length n over
of length n over  is a
is a  -constacyclic code if and only if
-constacyclic code if and only if  is a cyclic code of length 2n over R.
is a cyclic code of length 2n over R.
Proof. It is an immediately consequence of Lemma 3.2.
Now we define a Gray weight for codes over R as follows.
Definition 3.1. The gray weight on  is a weight function on R defined as
is a weight function on R defined as


Define the gray weight of a codeword
 to be the rational sum of the Gray weights of its components, i.e.
to be the rational sum of the Gray weights of its components, i.e.
 . The Gray distance
. The Gray distance  is given by
is given by . The minimum Gray distance of
. The minimum Gray distance of  is the smallest nonzero Gray distance between all pairs of distinct codeword of
is the smallest nonzero Gray distance between all pairs of distinct codeword of . The minimum Gray weight of
. The minimum Gray weight of  is the smallest nonzero Gray weight among all codeword of
is the smallest nonzero Gray weight among all codeword of . If
. If  is linear, the minimum Gray distance of
is linear, the minimum Gray distance of  is the same as the minimum Gray weight of
is the same as the minimum Gray weight of . The Hamming weight
. The Hamming weight  of a codeword
of a codeword  is the number of nonzero components in
is the number of nonzero components in . The Hamming distance
. The Hamming distance  between two codeword (
between two codeword ( and
and ) is the Hamming weight of the codeword
) is the Hamming weight of the codeword . The minimum Hamming distance d of
. The minimum Hamming distance d of  is define as min
is define as min (cf.[7]). It is obviously that for any codeword
(cf.[7]). It is obviously that for any codeword  of
of , we have
, we have .
.
Lemma 3.3. The gray map  is a distance-preserving map from (
is a distance-preserving map from ( , Gray distance) to (
, Gray distance) to ( , Hamming distance).
, Hamming distance).
Proof. Let . From the definition of
. From the definition of , we have
, we have

for any . Then
. Then

Corollary 3.1. The Gray image of a  -constacyclic code of length n over
-constacyclic code of length n over  under the Gray map is a distance invariant linear cyclic code of length 2n over R.
under the Gray map is a distance invariant linear cyclic code of length 2n over R.
4. (1 + 2v)-Constacyclic Codes of Length n over ( and Their Gray Images
In this section, we study (1 + 2v)-constacyclic codes of length n over  and their Gray images, where n is a positive integer which is not divisible by p, the characteristic of the residue field
and their Gray images, where n is a positive integer which is not divisible by p, the characteristic of the residue field . Two ideals
. Two ideals  of a ring R is called relatively prime if
of a ring R is called relatively prime if .
.
Lemma 4.1. ([8], Theorem 1.3). Let  be ideals of a ring R, The following are equivalent:
be ideals of a ring R, The following are equivalent:
1) For 
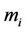 and
and  are relatively prime;
are relatively prime;
2) The canonical homomorphism  is surjective.
is surjective.
Let , then the canonical homomorphism
, then the canonical homomorphism  is bijective.
is bijective.
A finite family  of ideals of a commutative R, such that the canonical homomorphism of R to
of ideals of a commutative R, such that the canonical homomorphism of R to  is an isomorphism is called a direct decomposition of R. The next lemma is well-known.
is an isomorphism is called a direct decomposition of R. The next lemma is well-known.
Lemma 4.2. let R be a commutative ring,  a direct decomposition of R and M an R-module. With the notation we have:
a direct decomposition of R and M an R-module. With the notation we have:
1) There exists a family  of idempotents of R such that
of idempotents of R such that  for
for .
. and
and  for
for .
.
2) For , the submodule
, the submodule  is a complement in
is a complement in  of the submodule
of the submodule  so the
so the —modules
—modules  and
and  are isomorphic via the map
are isomorphic via the map

3) Every submodule N of M is an internal direct sum of submodules of , which are isomorphic via
, which are isomorphic via  with the submodules
with the submodules  of
of  (
( ). Each
). Each  is isomorphic to
is isomorphic to . Conversely, if for every
. Conversely, if for every ,
,  is a submodule of
is a submodule of , then there is a unique submodule
, then there is a unique submodule 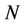 of
of , such that
, such that  is isomorphic with
is isomorphic with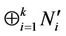 . Let
. Let , where
, where ,
, . Denote
. Denote ,
,
 . Let
. Let  be a (1 + 2v)-constacyclic codes of length n over
be a (1 + 2v)-constacyclic codes of length n over . Since
. Since , and
, and ,
,  then by Lemma 4.2, as a Â-submodule of
then by Lemma 4.2, as a Â-submodule of ,
,  , where
, where . If we denote
. If we denote , then it is obviously that
, then it is obviously that , hence
, hence  .
.
Theorem 4.1. Let  be a linear codes of length n over
be a linear codes of length n over . Then
. Then  is a (1 + 2v)-constacyclic code of length n over
is a (1 + 2v)-constacyclic code of length n over  if and only if
if and only if  and
and  are negacyclic and cyclic codes of length n over R respectively.
are negacyclic and cyclic codes of length n over R respectively.
Proof. Let , where
, where
 ,
,  ,
,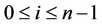 . Then
. Then ,
, . By the definition of the μ-constacyclic shift
. By the definition of the μ-constacyclic shift , we have
, we have
 , then
, then

and .
.
That means, if  is a (1 + 2v)-constacyclic codes of length n over
is a (1 + 2v)-constacyclic codes of length n over , then
, then  and
and  are negacyclic and cyclic codes of length n over R respectively. On the other hand, if
are negacyclic and cyclic codes of length n over R respectively. On the other hand, if , then
, then

that means, if  and
and  are negacyclic and cyclic codes of length n over R respectively, then
are negacyclic and cyclic codes of length n over R respectively, then  is a (1 + 2v)-constacyclic codes of length n over
is a (1 + 2v)-constacyclic codes of length n over .
.
Theorem 4.2. Let  be a (1 + 2v)-constacyclic code of length n over
be a (1 + 2v)-constacyclic code of length n over , then there are polynomials
, then there are polynomials  and
and  over R such that
over R such that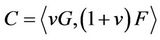 where
where  are pairwise coprime monic polynomials over R, such that
are pairwise coprime monic polynomials over R, such that ,
,  .
.
Proof. Since  is a (1 + 2v)-constacyclic code of length n over
is a (1 + 2v)-constacyclic code of length n over , then by Theorem 4.1,
, then by Theorem 4.1,  and
and  are negacyclic and cyclic codes of length n over R respectively, then by Lemma 2.2 and Lemma 2.5, there are polynomials
are negacyclic and cyclic codes of length n over R respectively, then by Lemma 2.2 and Lemma 2.5, there are polynomials  and
and

over R such that

where  are pairwise coprime monic polynomials over R, such that
are pairwise coprime monic polynomials over R, such that ,
, . For any
. For any , then
, then , there are
, there are  such that
such that  mod
mod ,
,
 mod
mod , that means, there are
, that means, there are  such that
such that


Since ,
,
 then
then

hence  mod
mod
 . So
. So
 .
.
On the other hand, For any
 then there are polynomials
then there are polynomials  such that
such that  mod
mod  then there are
then there are  such that
such that ,
,  , and there is
, and there is  such that
such that

then
 ,
,

this means , and
, and
 , hence
, hence
 then
then , so
, so . This gives that
. This gives that .
.
From Lemma 2.1, 2.4, and the proof of Theorem 4.2, we immediately obtain the following result.
Corollary 4.1. Let  be a (1 + 2v)- constacyclic codes of length n over
be a (1 + 2v)- constacyclic codes of length n over , then
, then
 .
.
Theorem 4.3. Let 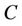 be a (1 + 2v)-constacyclic code of length n over
be a (1 + 2v)-constacyclic code of length n over , then there is a polynomial
, then there is a polynomial  over
over  such that
such that .
.
Proof. By Theorem 4.2, there are polynomials

and  over R such that
over R such that
 where
where  are pairwise coprime monic polynomials over R, such that
are pairwise coprime monic polynomials over R, such that ,
, .
.
Let , obviously,
, obviously,
 .
.
Note that
 then hence
then hence .
.
We now give the definition of polynomial Gray map over . For any polynomial
. For any polynomial  with degree less then n can be represented as
with degree less then n can be represented as , where
, where  and their degrees are less than n. Define the polynomial Gray map as follows:
and their degrees are less than n. Define the polynomial Gray map as follows:


It is obviously that  is the polynomial representation of
is the polynomial representation of .
.
Theorem 4.4. Let  be a (1 + 2v)- constacyclic code of length n over
be a (1 + 2v)- constacyclic code of length n over where
where

and

are polynomials over R, 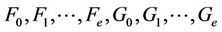 are pairwise coprime monic polynomials over R, such that
are pairwise coprime monic polynomials over R, such that
 ,
, .
.
If , then
, then where
where
 .
.
Proof. By Lemma 4.3, we know that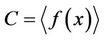 , where
, where . Let
. Let  be any element in
be any element in , where
, where  can be written as
can be written as ,
,  , it is obviously that
, it is obviously that  . Then we have
. Then we have

On the other hand, by Lemma 2.1, Lemma 2.5, Lemma 3.1 and Corollary 4.1, we know that


Hence,

We now study the dual codes of a (1 + 2v)-constacyclic code of length n over .
.
Since (1 + 2v)2 = 1, then the dual of a (1 + 2v)-constacyclic code is also a (1 + 2v)-constacyclic code. We have following result similar to Theorem 3.2 in [7].
Theorem 4.5. Assume the notation as Theorem 4.1. Let  be a (1 + 2v)-constacyclic code of length n over
be a (1 + 2v)-constacyclic code of length n over , Then
, Then .
.
By Theorem 4.5, Lemma 2.3 and Lemma 2.6, It is obviously that the above results of (1 + 2v)-constacyclic code can be carried over respectively to their dual codes. We list them here for the sake of completeness.
Corollary 4.2. Let  be a (1 + 2v)-constacyclic codes of length n over
be a (1 + 2v)-constacyclic codes of length n over , and
, and  are generator polynomials of
are generator polynomials of  and
and  respectively. Where
respectively. Where  and
and  are polynomials over R,
are polynomials over R,  are pairwise coprime monic polynomials over R, such that
are pairwise coprime monic polynomials over R, such that ,
,  .
.
Let
 ,
,
 ,
,

Then 1) .
.
2)  where
where .
.
3) .
.
4) .
.
5. Conclusion
In this paper, we establish the structure of (1 + 2v)-constacyclic codes of length n over  and classified Gray maps from (1 + 2v)-constacyclic codes of length n over
and classified Gray maps from (1 + 2v)-constacyclic codes of length n over  to
to , prove that the image of a (1 + 2v)-constacyclic codes of length n over R + vR under the Gray map is a distance-invariant linear cyclic code of length 2n over R, where R is a finite chain ring. The generator polynomial of this kind of codes of length n are determined and their dual codes are also discussed.
, prove that the image of a (1 + 2v)-constacyclic codes of length n over R + vR under the Gray map is a distance-invariant linear cyclic code of length 2n over R, where R is a finite chain ring. The generator polynomial of this kind of codes of length n are determined and their dual codes are also discussed.
NOTES