Comparative Assessment on the Performance of Open-Loop and Closed-Loop IFOGs ()
1. Introduction
Angular rotation in vehicles is one of the parameters that need to be accurately measured in order to describe the position of an object. Traditionally, the angular momentum of a spinning rotor was used to determine the angular rate or displacement [1-3]. These devices are susceptible to damage from shock and vibration, exhibit crossaxis acceleration sensitivity and, for the lower cost versions; they have reliability problems [3].
Directions around the same closed optical path will experience path length difference that is proportional to the rotation rate of the setup [4,5]. Sagnac shift is the common feature among optical gyros. Sagnac is now extensively used in commercial inertial navigation systems for aircraft. Given the advantage of this effect, the actual path length difference due to the rotation is quite small, e.g. the gyro used in the aircraft navigation must detect rotation rates below 0.01 deg/hr [6]. FOG is used for measurement of the rotation based on Sagnact Effect. Two types of FOG are used: the interferometric FOG (I-FOG) in which a low coherence light source is used and the resonance FOG (R-FOG). In the R-FOG the differences of resonance frequency caused by sagnact effect is utilized for measuring the rotation. Therefore even a short length of optical fiber is sufficient for the measurement. R-FOG needs a coherent light source for which such effects like Kerr effect and reflective optic phenomenon must be considered. The FOG converts the Sagnact phase shift into a beam frequency between the clockwise and counterclockwise of laser modes. This implies sensing path length changes of about one part in 1016, which corresponds to absolute length changes on the order of a nuclear dimension. Requirement of the precision of rotation measurement for spacecraft navigation lies between 0.01˚/hr to 0.001˚/hr.
The principle of operation of a typical fiber gyro is based on a phase modulation in both directions of an optical fiber loop, as if it acts as a delay line. The modulation frequency,  , matches the half period of the transit time
, matches the half period of the transit time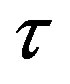 . Such a modulation scheme provides a sinusoidal response with a stable bias. However this response is nonlinear and the rotation rate proportional to the returning power is not perfectly stable.
. Such a modulation scheme provides a sinusoidal response with a stable bias. However this response is nonlinear and the rotation rate proportional to the returning power is not perfectly stable.
Ring laser gyroscope (RLG) consists of a ring laser having two counter-propagating modes over the same path in order to detect rotation. It works based on Sagnac shift effect and requires high vacuum and precision mirror technology, which makes this technique very expensive [4]. The physical principal of RLG operation is analogous to the Doppler Effect, but it involves determination of the phase shift between two counter-propagating light beams in an evacuated mirrored cavity [6]. To address this drawback, interferometric fiber optic gyro (IFOG) is employed whose function resembles RLG, notwithstanding the fact that, in IFOG, the same effect is obtained in a fiber coil with the elimination of the high voltage and high vacuum, which results in a low-cost inertial rotation sensor [4,6]. In addition, IFOGs are abstracted in miniature devices; all-solid state with a limited number of components, therefore lower cost.
In terms of light source, RLG requires an external narrow band gas laser with its active gain medium which is an integral part of the sensing cavity, whereas IFOG works with an external broadband light source [7]. Path length measurement in RLG is performed by measuring the difference of resonant frequencies between two cavities [5]. Despite, IFOG rotation rate sensing is achieved through a direct measurement (open loop) or nulling (close loop) of the optical phase difference due to the rotation-induced Sagnac phase shift [4,6,7].
According to the fact that high precision gyro is not always required, e.g. in land automotive vehicle an IFOG with the accuracy between 10 to 200 deg/hr is sufficient [8], and also regarding to the least requirements with the most flexibility in the design of IFOG, the improvement of this sensor becomes more sensible.
2. Principle of Operation
The principle of operation of an IFOG is based on the phenomenon that a circuital system has different optical path lengths in the two propagation directions when it rotates [9]. The difference between counter propagating beams provides the amount of the rotation. The main structure includes a laser diode, usually a super luminescent diode (SLD) or Rare-earth doped fiber with improved wavelength stability, a coupler to split light into clockwise and counterclockwise directions, a length of optical fiber wound on a coil as the rotation sensing loop, and a photo detector to convert optical information into electrical signals for further processing. Light source temperature is controlled by using a thermo electric cooler (TEC) and the detector is a PINFET module with a high sensitivity and hybrid trans-impedance amplifier. The type of the fiber optic and the way of winding specify the particular category that IFOG belongs to, which suits it to the specific application of the sensor [10]. A complete IFOG has identical optical paths in the clockwise and counter clock wise. In this IFOG known as “minimum configuration”, a polarizer and second coupler are employed [5,11].
Optical signal is received by the detector after passing through the fiber coil and couplers and converted into the electric current. An electrical amplifier is connected to the detector to change the current to the appropriate voltage. The obtained voltage is, then, amplified and fed into the signal processing circuit to extract the angular rotation rate [5,12].
EF-FOG work by frequent utilize of sagnact loop, in this manner output signal re-inputted as feedback. It performs like R-FOG but without high length coherence light source and never use the resonance effect. FE-FOG in comparison with Open-loop I-FOG has high sensibility and wide dynamic range. In this paper we compare the results of open loop and closed loop I-FOG.
A light source with a coherence length much shorter than the coil length allows only the wave pairs that have circulated the same number of times in the loop to interfere with each other and to produce an output related to the rotation-induced nonreciprocal phase shift. The resultant optical response is essentially the sum of all the optical responses of a series of conventional Sagnac Interferometric fiber-optic gyroscopes with their effective loop length in multiples of a single coil’s length. The multiple-trip interference and the associated intensity summation produces a response resembling a resonance phenomenon, with the strength and sharpness of the resonance increasing with the number of interfering light waves. The proposed gyro has different from a resonant fiber-optic gyro (R-FOG) because it uses a low coherent light source. The low coherent source minimizes not only errors from Rayleigh back scattering, but also bias errors caused by the optical Kerr effect. This could not possibly be done in an R-FOG because of high coherent light source.
If the modulation frequency of phase modulator in sagnact loop consists of whole loop time delay, the output signal in IFOG will be in pulse shape; therefore, when rotation occurs in the system, the location of output peak pulse shifts by sagnact effect. Precision of measurement depends on sharpness of the output pulses. Sharpness of output pulse is determined by the phase modulation depth and EFDA gain.
Miniature fiber optic gyros have also been manufactured with all solid-state optical devices for precise measurements of mechanical rotation based on the sagnac principle.
Open-loop IFOG is a simple configuration of the IFOG. Closed-loop IFOG performs similar to the resonance FOG (R-FOG), both based on Sagnac effect, although used for different tasks.
3. Rotation Equation
When the optical ring is rotated with a tangential velocity , the beam rotating with the ring will have an optical path longer than the counter-rotating beam by a distance
, the beam rotating with the ring will have an optical path longer than the counter-rotating beam by a distance  given by [1]:
given by [1]:
 (1)
(1)
where, R is the ring radius and c is the speed of light in the vacuum. For a monochromatic light of wavelength , this change in optical path length results in the Sagnac phase difference, which is given by Equation (2).
, this change in optical path length results in the Sagnac phase difference, which is given by Equation (2).
 (2)
(2)
The phase difference between two beams, after passing the ring with the area A and rotating with an angular velocity , generates a phase difference which is given by [1]:
, generates a phase difference which is given by [1]:
 (3)
(3)
It is important to note that, the resultant phase shift is independent of the medium and of the exact shape of the loop. This compliant property of the IFOG is an advantage when it is required to design it to fit the volume constrains in the specific applications [1]. However, the resultant phase shift can be increased by additional loops (turns of fiber) i.e. if it is wound N turns of the fiber coil. The resultant phase shift becomes [13]:
 (4)
(4)
Alternatively, we can express the resultant phase shift in terms of coil diameter and fiber length by noting that:
 (5)
(5)
And,
 (6)
(6)
So, the Sagnac phase shift can be rewritten as:
 (7)
(7)
As one example in a typical IFOG (200 m coil length, 10 cm-diameter coil) for measurement of the earth angular rotation ( = 15˚/h = 0.73 µr/s), the sensor detects a phase difference of
= 15˚/h = 0.73 µr/s), the sensor detects a phase difference of  = 36 µr, corresponding to an optical path difference of the order of 10 - 12 m [2,13].
= 36 µr, corresponding to an optical path difference of the order of 10 - 12 m [2,13].
Eventually the output signal for such configuration will be [2]:
 (8)
(8)
in which,  is the current obtained when the ring is at the rest.
is the current obtained when the ring is at the rest.
4. Open-Loop Configuration with Phase Modulation
As mentioned above, the major problem of the basic configuration is the output nonlinearity for small phase shift,  which hinders high sensitivity measurements of the small rotation angles [14]. This limitation is overcome by transforming the base band cosine-dependence into a sinusoidal function [1,3]. Although for translating the output signal from base band to a carrier at angular frequency
which hinders high sensitivity measurements of the small rotation angles [14]. This limitation is overcome by transforming the base band cosine-dependence into a sinusoidal function [1,3]. Although for translating the output signal from base band to a carrier at angular frequency , different solutions have been proposed, but today optical phase modulation technique is commonly used. The typical setup of a practical IFOG in all-fiber technology has a phase modulator which is inserted in the fiber coil close to a coupler output so that the phase delays are cumulated by the counter propagating waves. In all-fiber IFOG, phase modulator is constructed by winding and cementing a few fiber turns on a short, hollow piezoceramic tube (PZT). By applying a modulating voltage to the PZT, a radial elastic stress and a consequent optical path length variation due to the elasto-optic effect are generated [14].
, different solutions have been proposed, but today optical phase modulation technique is commonly used. The typical setup of a practical IFOG in all-fiber technology has a phase modulator which is inserted in the fiber coil close to a coupler output so that the phase delays are cumulated by the counter propagating waves. In all-fiber IFOG, phase modulator is constructed by winding and cementing a few fiber turns on a short, hollow piezoceramic tube (PZT). By applying a modulating voltage to the PZT, a radial elastic stress and a consequent optical path length variation due to the elasto-optic effect are generated [14].
5. The Open-Loop IFOG Modulation Equation
In this section, the modulation equations of extracting the phase shift are comprehensively described. In the configuration described in the previous section, the clockwise (CW) and counterclockwise (CCW) propagating waves experience a phase delay  and
and , respectively [15], where
, respectively [15], where  is the radiation transition time in a fiber with an overall length
is the radiation transition time in a fiber with an overall length . By applying a phase modulation at angular frequency
. By applying a phase modulation at angular frequency  , the modulation equation will be [16]:
, the modulation equation will be [16]:
 (9)
(9)
Here,  is the amplitude of modulation signal, and
is the amplitude of modulation signal, and  is the modulation frequency.
is the modulation frequency.
Therefore, CW and CCW waves are modulated as phase shift by  and
and , respectively. So, the modulation phase shift difference is as follows:
, respectively. So, the modulation phase shift difference is as follows:
 (10)
(10)
Finally, the total phase shift in the output signal will be:
 (11)
(11)
Now, the output signal will become:
 (12)
(12)
Considering the fact that the SLD switched by , with the help of Equations (9), (11) the phase shift becomes [16]:
, with the help of Equations (9), (11) the phase shift becomes [16]:
 (13)
(13)
 (14)
(14)
Substituting the amplitude with Equation (15) as follow [1]:
 (15)
(15)
The output current of photodiode becomes:
 (16)
(16)
Or can be rewritten as:
 (17)
(17)
Using the below Bessel equations:
 (18)
(18)
 (19)
(19)
Equation (17) can be rewritten in a way that one can easily extract the relevant harmonics [16]:
 (20)
(20)
To have an optimum sensitivity, output power, photon noise, and signal to noise,  is selected to be as [16]
is selected to be as [16]
 (21)
(21)
To simplify Equation (20), we consider fmod = fp [1,16]. Using this assumption and Equation (15), we will have:
 (22)
(22)
The amplitude of the output signal at fmod, which gives the first harmonic of the output current, i.e. Equation (20) will be [2]:
 (23)
(23)
 (24)
(24)
Table 1 shows the four harmonics generated in the photodiode output current [2]:
Now, we can calculate  by H1 with the below equation [2,16]:
by H1 with the below equation [2,16]:
 (25)
(25)
 Could be also obtained with another approach using H1, H2, J1 and J2 [16]:
Could be also obtained with another approach using H1, H2, J1 and J2 [16]:
 (26)
(26)
A comfort and reliable method is proposed here is to use H1, H2, H3 and H4 to calculate  with the help of the solution of Equation (27) and Table 1 [2,16]:
with the help of the solution of Equation (27) and Table 1 [2,16]:
 (27)
(27)
 (28)
(28)
 (29)
(29)

Table 1. Harmonics of the photodiode output current. Ci = C, i = 0, ···, 4.
 (30)
(30)
Owing to this, the Sagnac shift is obtained as Equation (31) which is the best suited for hardware implementation:
 (31)
(31)
6. Evaluation of Digital Filtering in an Open-Loop IFOG
The simulation results of the abovementioned procedure show that, this approach can perfectly be employed in the signal processing part of IFOGs. To achieve the required harmonics, four digital filters are designed. These filters were designed by SPtool in Matlab 7a. Since the phase linearity of the filters was important, finite impulse response (FIR) filters were taken into account to have the four required band pass filters. Regarding to the available data the beneath quantities are listed as input of the simulation:
Input rotation rate = 10 deg/s (AHRS range);
Coil length = 500 m;
Coil diameter = 10 cm;
Sampling frequency = 10 MHz;
Time domain = 2 ms;
Wave length = 1310 nm;
Refractive index of optical fiber core = 1.43;
Coil length transient time = (500/3e8) × 1.43.
The coil frequency is obtained as  . As mentioned before, this frequency is the PZT vibration and SLD switch frequency, as well.
. As mentioned before, this frequency is the PZT vibration and SLD switch frequency, as well.
Figure 1 shows the designed band pass filters with the same bandwidth (0.208 MHz) but different central frequencies. In the filters in Figure 1, Fp and Fs are, pass band frequency and stop band frequency, respectively. Also, Rp and Rs are ripples in pass band and stop band.
The filters are described as follows:
1) Band pass filter: Gain = 1, central frequency = 0.208 MHz;
2) Band pass filter: Gain = 1, central frequency = 0.416 MHz;
3) Band pass filter: Gain = 1, central frequency = 0.624 MHz;
4) Band pass filter: Gain = 1, central frequency = 0.832 MHz.
To extract the four harmonics from the IFOG output current, the filters are implemented by considering the direct form structure. Figure 2 shows the amplitude of the filtered signals, H1 to H4. In the next step, rotation rate , is calculated using H1 to H4 with the help of Equations (7) and (31).
, is calculated using H1 to H4 with the help of Equations (7) and (31).
The comparison of calculated  with the input rotation rate, i.e. 10 deg/s showed one percent difference. This discrepancy caused from utilizing unsharp filters. As it has been experienced, we will reach to the better accuracy if higher order filters are considered.
with the input rotation rate, i.e. 10 deg/s showed one percent difference. This discrepancy caused from utilizing unsharp filters. As it has been experienced, we will reach to the better accuracy if higher order filters are considered.
7. Closed-Loop EF-FOG Configuration and Operation
In this structure the weak feedback signal is amplified by the Er-Doped Fiber Amplifier (EDFA) to prevent the laser scattering. Fiber amplifier is assumed to be linear, which means there are no gain effects. The output signal is the sum of interferometric CW and CCW beams in the total route. The modulator is located in sagnac loop. If the phase modulator frequency is selected properly, the output signal will be a series of short pulses [17]. Hence modulation frequency of phase modulator and route delay must be approved by the equation  where
where  is angular frequency of the phase modulation, and
is angular frequency of the phase modulation, and  is the time delay in whole round trip loop consisting of Sagnac loop and amplified fiber optic loop. If the sharpness of output pulses could not be adjusted by phase modulation, by changing EFDA gain it can be compensated. If this equation
is the time delay in whole round trip loop consisting of Sagnac loop and amplified fiber optic loop. If the sharpness of output pulses could not be adjusted by phase modulation, by changing EFDA gain it can be compensated. If this equation  is not realized, for example due to detuning, there will be a phase shift
is not realized, for example due to detuning, there will be a phase shift  that can be demodulated as an error signal for phase modulated (PM) technology. The operation of the FEFOG is sensitive to the EDFA gain [18]. In theory the first intereferometric output signal without feedback is equal to ordinary IFOG as:
that can be demodulated as an error signal for phase modulated (PM) technology. The operation of the FEFOG is sensitive to the EDFA gain [18]. In theory the first intereferometric output signal without feedback is equal to ordinary IFOG as:
 (32)
(32)
where v is the interferometric coefficient and K1 is a parameter that expresses the loss resulting from the Sagnac loop and the couplers of the Sagnac interferometer,  is the modulation frequency,
is the modulation frequency,  is the effective phasemodulation depth, which is expressed as
is the effective phasemodulation depth, which is expressed as
 (33)
(33)
 is the wave-propagation time through the Sagnac loop (please note the difference with the total time roundtrip delay t) and is expressed as
is the wave-propagation time through the Sagnac loop (please note the difference with the total time roundtrip delay t) and is expressed as  (where L is the length of Sagnac loop), and
(where L is the length of Sagnac loop), and  is the phase-modulation depth.
is the phase-modulation depth.  is the Sagnac phase shift induced by rotational movement, which is expressed as Equation (7) in the previous section.
is the Sagnac phase shift induced by rotational movement, which is expressed as Equation (7) in the previous section.
By considering the effect of optical feedback, the second-time interference signal experienced after the feedback has been derived is
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 1. Band pass filters for extracting four harmonics from the photocurrent IFOG signal. FIR filter design is taken into account as these filters have phase linearity. (a) Band pass filter (harmonic 1) Kaiser window FIR with order = 100, Fp1 = 0.202 MHz, Fp2 = 0.21 MHz, Fs1 = 0.334MHz, Fs2 = 0.399 MHz, Rp = 0.3917, Rs = 39.45, Phase Delay = −0.255 rad; (b) Band pass filter (harmonic 2) Kaiser window FIR with order = 153, Fp1 = 0.4 MHz, Fp2 = 0.43 MHz Fs1 = 0.249 MHz, Fs2 = 0.587 MHz, Rp = 0.3276, Rs = 40.97, Phase Delay = −1.159 rad; (c) Band pass filter (harmonic 3) Kaiser window FIR with order = 162, Fp1 = 0.597 MHz, Fp2 = 0.653 MHz, Fs1 = 0.457 MHz, Fs2 = 0.802 MHz, Rp = 0.33, Rs = 40.29, Phase Delay = −0.361 rad; (d) Band pass filter (harmonic 4) Kaiser window FIR with order = 148, Fp1 = 0.802MHz, Fp2 = 0.849MHz, Fs1 = 0.650 MHz, Fs2 = 1.71MHz, Rp = 0.32, Rs = 40.25, Phase Delay = −0.612 rad.
and the third-time interference signal that occurs after feedback has been twice derived is
 (35)
(35)
where A is the gain of the fiber amplifier and K2 is a parameter that depends on the coupling ratio of the feedback couplers and the transmission loss in the feedback loop. For simplicity, we assume that . The total output at the photodetector is the summation of the number of above-mentioned interferences and is expressed as
. The total output at the photodetector is the summation of the number of above-mentioned interferences and is expressed as
 (36)
(36)
If , the total photodetector output can be realized by proper adjustment of the modulation frequency to match the round-trip time, and we can have
, the total photodetector output can be realized by proper adjustment of the modulation frequency to match the round-trip time, and we can have
 (37)
(37)
where K is the photodetector coefficient, because the total output is a series of short pulses, we can determine the peak value through the following equation:
 (38)
(38)
Above Equation is a condition required to find the peak position of the output pulse that is valid for both cases of rotation and nonrotation, please note that only those equations of even p correspond to the peak position. From this equation and condition we can see that the output pulse shifts if rotation occurs.
For Open-Loop Method for the FE-FOG In Equation (33) if  is selected to be between
is selected to be between  and
and  there is no rotation, Equation (33) is satisfied only when n = 0. In this case, the peak positions of the output pulse are determined through the following equation:
there is no rotation, Equation (33) is satisfied only when n = 0. In this case, the peak positions of the output pulse are determined through the following equation:
 (39)
(39)
Here  represents the peak positions corresponding to the nonrotation case and i denotes the peak number of the output pulse in the time axis. We see that the peak positions are not affected by the phase-modulation depth
represents the peak positions corresponding to the nonrotation case and i denotes the peak number of the output pulse in the time axis. We see that the peak positions are not affected by the phase-modulation depth  when there is no rotation. On the other hand, when rotation occurs (
when there is no rotation. On the other hand, when rotation occurs ( ) the peak positions are affected by the Sagnac phase shift and can be determined by
) the peak positions are affected by the Sagnac phase shift and can be determined by
 (40)
(40)
where  denotes the peak positions when rotation occurs and i has the same meaning as in Equation (39) Comparing Equations (39) and (40), we see that the peak positions shift if rotation occurs, and the shift of the peaks is just equal to
denotes the peak positions when rotation occurs and i has the same meaning as in Equation (39) Comparing Equations (39) and (40), we see that the peak positions shift if rotation occurs, and the shift of the peaks is just equal to . Therefore, the peak positions are in fenced by only the Sagnac phase shift if rotation occurs and if we fix the phase-modulation depth
. Therefore, the peak positions are in fenced by only the Sagnac phase shift if rotation occurs and if we fix the phase-modulation depth . We can thus determine the rotation rate by the detection of the peak shift
. We can thus determine the rotation rate by the detection of the peak shift  of the output pulse.
of the output pulse.
In this paper the wave-length of optical source is , the modulation frequency of the phase modulator,
, the modulation frequency of the phase modulator,  (
( ), and the radius of the Sagnac loop is R = 0.05 m. The round-trip length is 500 m, which is selected to match the modulation frequency for the pulse output, of which the Sagnac-loop length is 460 m and the length of the EDFA (including the pigtail of couplers) is 40 m. The interferometric coefficient is v = 0.96, the photodetection coefficient is K = 0.2, the parameter K = 0.06, the effective phase-modulation depth is
), and the radius of the Sagnac loop is R = 0.05 m. The round-trip length is 500 m, which is selected to match the modulation frequency for the pulse output, of which the Sagnac-loop length is 460 m and the length of the EDFA (including the pigtail of couplers) is 40 m. The interferometric coefficient is v = 0.96, the photodetection coefficient is K = 0.2, the parameter K = 0.06, the effective phase-modulation depth is , and the Sagnac phase shift is
, and the Sagnac phase shift is  for the nonrotation case.
for the nonrotation case.
Figure 3 demonstrates the principle of the rotation measurement for the open-loop method when the output pulse is shifted by rotation. The plots are normalized and . We see that the peak position shifts if rotation occurs, phase shift 0˚/h and 3.6˚/h. Further calculations show that the shift is increased as the rotation rate increases. The very sharp peak of the output pulse can result in a high-resolution rotation measurement. From Equations (7) and (38)-(40) (in equation (39), i = 0, 2, 4), we can derive the rotation rate as:
. We see that the peak position shifts if rotation occurs, phase shift 0˚/h and 3.6˚/h. Further calculations show that the shift is increased as the rotation rate increases. The very sharp peak of the output pulse can result in a high-resolution rotation measurement. From Equations (7) and (38)-(40) (in equation (39), i = 0, 2, 4), we can derive the rotation rate as:

Figure 3. rotation measurement for open-loop IFOG.
 (41)
(41)
where  is the time shift of the output peak as a result of the rotation, In Closed-Loop Method for the FE-FOG, we selected
is the time shift of the output peak as a result of the rotation, In Closed-Loop Method for the FE-FOG, we selected  with a condition of
with a condition of . In such a case the output pulse is shifted by only the rotation. In this section, we hope to show that the output pulse is affected by both rotation and phase modulation, so that we can use the phase modulation to compensate the Sagnac phase shift. Such a technical idea is consistent with the closed-loop method.
. In such a case the output pulse is shifted by only the rotation. In this section, we hope to show that the output pulse is affected by both rotation and phase modulation, so that we can use the phase modulation to compensate the Sagnac phase shift. Such a technical idea is consistent with the closed-loop method.
In Equation (38), if we assume that  (nonrotation) and we select
(nonrotation) and we select , e.g.,
, e.g.,  , then Equation (38), can be satisfied by n = 1, n = 0, and n = −1, which means that the output pulse has three kinds of peaks. The peaks corresponding to n = 0 have the same properties as do those of the open-loop method and will not be affected by the phase modulation; however, the peaks corresponding to n = 1 or n = −1 will be in fenced by both the Sagnac phase shift and the phase-modulation depth. This performance can be used for the rotation measurement.
, then Equation (38), can be satisfied by n = 1, n = 0, and n = −1, which means that the output pulse has three kinds of peaks. The peaks corresponding to n = 0 have the same properties as do those of the open-loop method and will not be affected by the phase modulation; however, the peaks corresponding to n = 1 or n = −1 will be in fenced by both the Sagnac phase shift and the phase-modulation depth. This performance can be used for the rotation measurement.
Figure 4 shows that the output pulses related to  is simple, but, the output pulses related to
is simple, but, the output pulses related to  are complicated and consist of three kinds of peaks designated A, B, and C. (Note: if we select
are complicated and consist of three kinds of peaks designated A, B, and C. (Note: if we select  to be greater than
to be greater than , even more output peaks will appear, because in Equation (38) n also includes integers over. This case can also be analyzed similarly). The peak positions for A, B, and C are determined by n = 1, 0, −1, respectively, in Equation (38). In this paper, we look at the peak positions corresponding to peaks A (peaks C also have similar properties). In one time period, peaks A also consist of two additional peaks, marked with circles and squares, whose positions are determined by
, even more output peaks will appear, because in Equation (38) n also includes integers over. This case can also be analyzed similarly). The peak positions for A, B, and C are determined by n = 1, 0, −1, respectively, in Equation (38). In this paper, we look at the peak positions corresponding to peaks A (peaks C also have similar properties). In one time period, peaks A also consist of two additional peaks, marked with circles and squares, whose positions are determined by
 (42)
(42)
N = 0, 1, 2, ··· respectively. If the Sagnac phase shift induced by rotation is canceled by the phase modulation of the phase modulator, the peak positions corresponding to peaks A will not shift in spite of rotation’s occurring. To realize this phase compensation we can feed back an electrical signal at the phase modulator. The rotation rate can thus be evaluated through the value of the phase modulation. Further calculations also show that, although in the closed-loop case (when both rotation and feedback control of  occur) peaks B and C are shifted, they cannot cross with peaks A. This is because, for in any case, the peak positions of peaks A, B, and C are determined from Equation (38) with n = 1, 0, −1, respectively, and they always have different values. The above result
occur) peaks B and C are shifted, they cannot cross with peaks A. This is because, for in any case, the peak positions of peaks A, B, and C are determined from Equation (38) with n = 1, 0, −1, respectively, and they always have different values. The above result
tells us that in the closed-loop case the dynamic range is large.
A more detailed mathematical description is presented in the following paragraphs. We first consider the case of nonrotation ( , for which the peak positions corresponding to peaks A can be determined by
, for which the peak positions corresponding to peaks A can be determined by
 (43)
(43)
where  is the phase-modulation depth corresponding to the nonrotation case. On the other hand, when rotation occurs and if the electrical-feedback signal is placed on the phase modulator, the peak positions corresponding to peaks A will not change, and we then have
is the phase-modulation depth corresponding to the nonrotation case. On the other hand, when rotation occurs and if the electrical-feedback signal is placed on the phase modulator, the peak positions corresponding to peaks A will not change, and we then have
 (44)
(44)
and from Equations (43) and (44) we can further derive
 (45)
(45)
We can evaluate the rotation rate by detecting .
.
Figure 5 shows the variation of the phase-modulation depth  as a function of the rotation rate for the closed loop. Figure 5(a) shows the output pulse when the rotation doesn’t exist
as a function of the rotation rate for the closed loop. Figure 5(a) shows the output pulse when the rotation doesn’t exist  and
and  and Figure 5(b) shows the output pulse when rotate without electric feedback signal in phase modulator Ω = 3.65˚/h and
and Figure 5(b) shows the output pulse when rotate without electric feedback signal in phase modulator Ω = 3.65˚/h and  therefore when rotation occur output pulses shifted. We can see the peak that shifted by rotation could back to the first position that
therefore when rotation occur output pulses shifted. We can see the peak that shifted by rotation could back to the first position that  shows the variation of phase modulation induced by electric
shows the variation of phase modulation induced by electric
feedback, that means the rotation rate of Ω = 3.65˚/h needs the phase compensation  .
.
8. Conclusions
In this paper, a comprehensive formulation of open loop interferometric fiber optic gyroscope (IFOG) was studied. Through the signal processing explanation, an accurate approach was proposed to calculate the phase shift to make the hardware implementation simpler. The simulation results of the digital signal processing using FIR filters showed that the chosen computational method to extract Sagnac shift from IFOG signal current is promising. With pointing out the similarities and differences between calculated  with the input rotation rate of 10 deg/s, and the output of the digital filtering approach, just a slight difference of less than 1% was observed. This distinction appeared because of using unsharp filters. Regarding to the experiences, we will have more accurate IFOG if higher order of filters are utilized.
with the input rotation rate of 10 deg/s, and the output of the digital filtering approach, just a slight difference of less than 1% was observed. This distinction appeared because of using unsharp filters. Regarding to the experiences, we will have more accurate IFOG if higher order of filters are utilized.
Also the functionality of the closed-loop fiber-optic gyroscope (I-FOG), based on multiple utilizations of the Sagnac loop and amplified optical feedback, has been proposed and theoretically investigated. The new gyroscope is termed as feedback Er-doped fiber-optic amplifier (FEDFA). A low-coherence light source is used in this FOG [19]. Amplification of a weak feedback gyroscope signal is performed by the incorporated EDFA. The final gyroscope output is pulsed if the modulation frequency of the phase modulator matches the round-trip time [20]. Sagnac phase shift can induce a shift of the output pulse, which is used for the rotation measurement.