A Wave Group for Entanglement, Linking Uncertainties in Time and Space ()
1. Introduction
Contrary to the claim by Von Neumann that hidden variables are incompatible with quantum mechanics1, Einstein et al. “were led to conclude that the description of reality as given by a wave function is not complete” [1]. Their conclusion depended on an analysis of extended plane waves due to more than one particle, and their supposition of entanglement at a distance has been supported by studies on hidden variables [2,3]. Further support has come recently from experimental applications directed at communications [4-6]. In these applications, electron spin up or down, is a digital memory marker that is accessible by optics. Spin is ‘remembered’ by photons after time delay. Since entanglement occurs, it is natural to consider further details of the propagation in both the photons and the particles. Other doubts about the completeness of quantum mechanics have arisen through recent experiments by Faipour et al. [7] on “weak measurements” of photon momentum. There have moreover been theoretical developments in wave equations for the electron including a treatment of wave packets [8]. Here we consider, by means of a wave group, a variable that, while predictable in wave mechanics is unmeasurable in principle, though having explanatory power. The problem is significant for electron beam interactions in transmission electron microscopy when modeled by track structure methods [9], where the location of atomic species depends on impact parameters. These are unobservable in the Bethe theory that is usually used to calculate cross-sections.
Quantum mechanics has had fundamental successes in innumerable ways. Early on, it provided explanations for spin and magnetic moment from the relativistic Hamiltonian and it provided many details in atomic spectra including the Lamb shift in hydrogen. Continued developments have been core to understanding quantum electrodynamics, nuclear interactions and high energy physics. Nevertheless, there are important features that remain mysterious. Whereas the origin of the wave function in electromagnetism is firmly based in Maxwell’s equations, the nature of mass and its probability amplitude contains undefined oscillations. Added to these are chronic disagreements about determinism [10-14]. Such shortcomings justify returning sometimes to basics to review what might have been discarded because not needed at the time.
In particular there are anomalies in Dirac’s formal treatment of quantum mechanics [15]. For example, he derives a mean velocity for the free electron equal to the speed of light, which he acknowledges to be experimentally unphysical. He goes on to show that there are two velocities, one “oscillatory part” with high frequency; the other a “constant part” with lower frequency. These are the two frequencies that we will examine in detail. Others have commented on this anomaly and attempted to find a resolution by a double frequency wavepacket [8]. We consider how a continuous wave group provides a more consistent description of the complicated velocities that Dirac tried to describe. We will see that the treatment has further implications for uncertainty in measurement.
In quantum mechanics, the wave vector k in the wave function of a photon or free particle is, typically, a real and measurable number and so also is the angular frequency w. The first depends, through the De Broglie hypothesis, on momentum, and is fundamental to optical, neutron and electron diffraction spectrometries. Where there is wavelength, there must also be frequency. What is it? In the photoelectric effect, energy is related to frequency through Planck’s law, E = hv, where h is Planck’s constant. Meanwhile, the eigenvalue for Schroedinger’s equation operating on the hydrogen atom gives a ground state binding energy of 13.6 eV. So when an electron is photo-ionized the photon frequency corresponds to the change in frequency of the ionized electron, and is consistent with Schroedinger’s time dependent equation,  , where
, where  = h/2p. In order to match the energy equation for a free particle in special relativity,
= h/2p. In order to match the energy equation for a free particle in special relativity,
 , (1)
, (1)
corresponds with:
 . (2)
. (2)
where c is the speed of light, m0 is the electron rest mass and momentum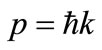 . The mass energy is added to binding energy. In a free particle, the ratio of energy to momentum,
. The mass energy is added to binding energy. In a free particle, the ratio of energy to momentum,  , is the phase velocity, both variables being conserved quantities. In the Hamiltonian for the wave equation, the operators for w and k commute, so their eigenvalues are independently measurable. Turning from electromagnetism to particles, vp =w/k is faster than the speed of light which is one reason why, following the theory of relativity, this velocity can neither transfer energy nor be directly measured. The velocities that we are familiar with in macroscopic physics are the group velocities [16,17], vg = dw/dk, including the velocity dependence of magnetic forces. What reality, then, can the ratio of two real and measurable numbers have?
, is the phase velocity, both variables being conserved quantities. In the Hamiltonian for the wave equation, the operators for w and k commute, so their eigenvalues are independently measurable. Turning from electromagnetism to particles, vp =w/k is faster than the speed of light which is one reason why, following the theory of relativity, this velocity can neither transfer energy nor be directly measured. The velocities that we are familiar with in macroscopic physics are the group velocities [16,17], vg = dw/dk, including the velocity dependence of magnetic forces. What reality, then, can the ratio of two real and measurable numbers have?
2. Electromagnetic Waves
In electromagnetic waves, where m0 = 0, Equation (2) yields, in the direction of propagation:
 (3)
(3)
where the speed of light in vacuo is calculated from Maxwell’s equations, e.g. [18]. It is a physical property, invariant in all inertial reference frames. In a medium of refractive index n = 1.47, we find in Figure 1 that the transmission from left to right through a glass block proceeds with the centre of the wave group phase locked. The four examples at different moments in time are se-

Figure 1. Simulation examples, at four moments in time, of vertically polarized electromagnetic wave group, after transmission (right of vertical line) and reflection from the surface of a glass block. The wave length shortens in the block. Alternating colors signify alternating signs of amplitude. The phase of the carrier wave and peak of the group progress in unison with equal velocities. Separation of reflected wave (left) and transmitted wave (right) increases with time.
lected from hundreds. Notice that the reflected wave proceeds backwards and that the progress of time is marked by increasing separation from the transmitted wave group. The simulation, by finite difference time domain methods encoded in the MEEP program [19], shows that vp = vn and
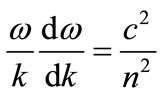 (4)
(4)
Equation (4) is consistent with Foucault’s experiment which showed the speed of light is slower in water than in air [16]. At the time of its demonstration, this fact seemed to confirm Huygen’s wave theory of light and disprove Newton’s corpuscular theory. As is now well known, the wave group combines elements of both theories and further details are examined below.
Meanwhile, several interesting anomalies arise and we mention three: firstly, when wave fronts of light intersect at an angle, their intersection travels faster than c. If the angle between propagation vectors is 90˚, the intersection of the waves moves at the speed 21/2c. The intersection cannot be observed because of quantization: energy is carried by the respective wave packets (Section 4) at speed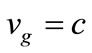 , so the transport of energy remains within rules determined by special relativity [20]. The high speed at the intersection is an example of a physical description not of an “event”, because energy is not transferred. Secondly when n < 1, as in the x-ray region of the radiation spectrum, vg > c but transport is limited by absorption. Likewise and thirdly, when dw/dk is greater than c, as happens, for example, in the incidence of ultraviolet light near the fundamental edge of ionic solids such as the alkali halides or PbF2 [21,22]. Again vg > c, but absorption is also high and this again limits the transport of information, where the mean free path is ~10 mm deep or 50 wave lengths.
, so the transport of energy remains within rules determined by special relativity [20]. The high speed at the intersection is an example of a physical description not of an “event”, because energy is not transferred. Secondly when n < 1, as in the x-ray region of the radiation spectrum, vg > c but transport is limited by absorption. Likewise and thirdly, when dw/dk is greater than c, as happens, for example, in the incidence of ultraviolet light near the fundamental edge of ionic solids such as the alkali halides or PbF2 [21,22]. Again vg > c, but absorption is also high and this again limits the transport of information, where the mean free path is ~10 mm deep or 50 wave lengths.
Whether or not the rule that information is not transported at speeds greater than c is broken, the physical laws remain invariant in all inertial reference frames. The relationships become more complicated for a different wave with rest mass m0 > 0, i.e. the probability amplitude for particles. Electrons in transmission microscopy diffract like light waves, but a comparison of the two wave velocities is illustrated in Figure 2 using units h = c = 1. For any particle with rest mass m0, since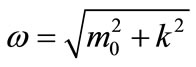 the lower trace in Figure 2(a) shows w dependence when m0 = 0, i.e. for light. The upper trace shows the dependence for a particle with m0 = 1. Meanwhile in Figure 2(b) when m0 = 1, since
the lower trace in Figure 2(a) shows w dependence when m0 = 0, i.e. for light. The upper trace shows the dependence for a particle with m0 = 1. Meanwhile in Figure 2(b) when m0 = 1, since ,
,  , then vp = 1/vg.
, then vp = 1/vg.
3. Probability Amplitudes
Following Equations (1) and (3) and knowing that group velocities are the classical velocities of particles, their phase velocities, vp = c2/vg, are faster than c. Whereas in electromagnetism both vg and vp are in principle measurable, in particles only vg is directly accessible. However, the phase velocity vp can be calculated as the product of known or assumed frequencies with corresponding wave lengths measured in electron microscopy. One consequence for Equation (3) is that the phase and group velocities have the same sign and so travel in the same direction.
Meanwhile, rest mass, m0, is a kind of fifth dimension as implied by both Equation (1), and by Dirac’s relativistic equation for the electron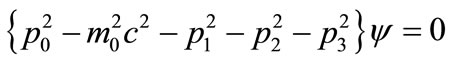 , [15] where p0 is the operator for energy and p1, p2 and p3 are momentum operators. Relativistic mass,
, [15] where p0 is the operator for energy and p1, p2 and p3 are momentum operators. Relativistic mass,  , varies continuously since it includes kinetic energy; but m0 has discrete values as in the standard model for elementary particles [23], or atomic nuclei. Changes in the rest mass correspond to heat released in nuclear reactions. The five dimensions are represented on two independent graphs in Figure 3(a), where the momentum is the resultant of the first graph and this resultant is included in the second graph. We include energies for antimatter [15], but leave aside the prediction of embedded dimensions supposed in string theory [24].
, varies continuously since it includes kinetic energy; but m0 has discrete values as in the standard model for elementary particles [23], or atomic nuclei. Changes in the rest mass correspond to heat released in nuclear reactions. The five dimensions are represented on two independent graphs in Figure 3(a), where the momentum is the resultant of the first graph and this resultant is included in the second graph. We include energies for antimatter [15], but leave aside the prediction of embedded dimensions supposed in string theory [24].
With this view, conservation of energy implies conservation of frequencies summed over all particles including photons, phonons etc. Likewise, conservation of
 (a)
(a) (b)
(b)
Figure 3. (a) Five dimensions in two graphs: (left) resultant of three spatial dimensions; and (right) the constraint of time through angular frequency ω on the momentum vector. The illustration is local for a particle in free-fall, or for an antiparticle represented by negative mass [16] at right; (b) Dimensions for a particle in an accelerating field (left) that produces increased energy and momentum. In a bound state (right), ω is reduced but partly compensated by the mean kinetic energy in  given by the virial theorem.
given by the virial theorem.
momentum implies conserved sums of individual wave vector components, 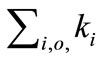 with dimensional i = 1, 2, 3 and summed over all particles o. Assuming the conservation laws determine the wave mechanical variables, then entanglement of particle phases is, in principle, as likely as has been observed with photons. In this way, phase information at a time B,
with dimensional i = 1, 2, 3 and summed over all particles o. Assuming the conservation laws determine the wave mechanical variables, then entanglement of particle phases is, in principle, as likely as has been observed with photons. In this way, phase information at a time B,  , may be “remembered” after an event at A; and—in case of thermal isolation and absenting secondary disturbance—may not be lost entirely upon measurement as in conventional quantum theory.
, may be “remembered” after an event at A; and—in case of thermal isolation and absenting secondary disturbance—may not be lost entirely upon measurement as in conventional quantum theory.
Moreover, relative phase and group velocities define mass:
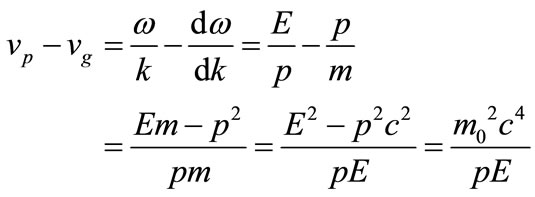 (5)
(5)
This equation is consistent with the fact that m0 = 0 in electromagnetism when w and k follow Maxwell’s equations. The relative speed separation, vp – vg, in the laboratory frame; translates to  and
and  in the particle rest frame. Then, within the particle wave group, time becomes Newtonian.
in the particle rest frame. Then, within the particle wave group, time becomes Newtonian.
Beyond this definition of mass, phase velocity allows a solution to the following problem. Consider, in the transmission electron microscope, a single electron that interacts with a foil oriented to a two beam Bragg condition. Let the microscope be selected for diffraction mode so that the electron must strike the photo receptor in one of two positions, A or B. If the electron creates an event in A, how is the information passed to position B, with speed less than c, so that it does not create a second event with multiplication of the electron and with failure of mass conservation? It is not necessary to posit a hidden condition to ensure compliance, since the above working includes another reason. The apparently instantaneous transport of information is a consequence of alternative reference frames: in the rest frame of the electron, vp, on the horizontal plane, is infinite, so that the wave front of the electron probability amplitude arrives instantaneously and connects A with B. By conservation, energy which is deposited in an event at A is not simultaneously available at B, and vice versa. In the electron rest frame the two beams at the plane of detection are contemporaneous where the reduction of the wave packet occurs in phase space; whereas in the laboratory rest frame the two locations are separated in time.
4. Velocity in a Symmetric Wave Group
A wave group in which the wave function is represented by:
 (6)
(6)
where the argument, X = k∙r – wt, with precise mean wave vector k' and with precise mean angular frequency w'. The real part of exp(iX) peaks when k'∙r = w't, and the carrier wave velocity vp = w'/|k'|. Here σ which determines the width of the Gaussian distribution, is written as single valued in the direction of wave propagation, though it is typically four dimensional. Because X describes a phase it is, by default, Lorentz invariant. Next normalize the equation for a single particle. Then for the simplest one-dimensional example in the direction of propagation [25]:
 (7)
(7)
Meanwhile, the expected energy  as in Planck’s law, while
as in Planck’s law, while  gives expected momentum in one dimension, consistent with the De Broglie hypothesis. The symmetric wave packet envelope is selected for simplicity. The Gaussian function is typical for random or spontaneous events, but others such as the defined electric pulse that produces synchrotron radiation [17,26], can be applied instead.
gives expected momentum in one dimension, consistent with the De Broglie hypothesis. The symmetric wave packet envelope is selected for simplicity. The Gaussian function is typical for random or spontaneous events, but others such as the defined electric pulse that produces synchrotron radiation [17,26], can be applied instead.
The envelope includes uncertainty in measurement. Letting t = 0 in Equation (4), and taking the direction of propagation x, the Fourier transform
 (8)
(8)
By adopting a definition,  where
where  falls to 1/e of its maximum, and likewise
falls to 1/e of its maximum, and likewise , the product,
, the product,  , as in the Heisenberg Uncertainty principle. By the same argument, at x = 0,
, as in the Heisenberg Uncertainty principle. By the same argument, at x = 0, 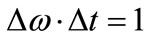 for a free particle as before. By contrast, the Heisenberg uncertainty principle applies equally to bound and free-particle states, though the present treatment can be easily extended. A second significant difference lies in extended uncertainties involving both t and w along with associated emission constants si A third difference is that the phase information in Equation (6) is retained in isolated systems, e.g. at low temperatures. As these differences hold, uncertainty depends on the probability amplitude.
for a free particle as before. By contrast, the Heisenberg uncertainty principle applies equally to bound and free-particle states, though the present treatment can be easily extended. A second significant difference lies in extended uncertainties involving both t and w along with associated emission constants si A third difference is that the phase information in Equation (6) is retained in isolated systems, e.g. at low temperatures. As these differences hold, uncertainty depends on the probability amplitude.
5. Discrete Representation
So far, the wave function has been treated as continuous; but it could also be represented as a sum of discrete states. These states could be quantized bound states in an atom or they might be high energy electrons elastically scattered as Bloch waves in a crystal. For a free particle, k and w are constants of motion so its wave function may be written:
 (9)
(9)
and phase velocity defined by a combined operation
 (10)
(10)
Calculation of the combined expected value for group velocity is only a little more complicated. One route is based on the relativistic equation , so that
, so that . When, in one dimensioneigenvalues are derived from the operator:
. When, in one dimensioneigenvalues are derived from the operator:

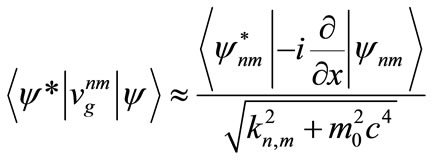 (11)
(11)
As 
 , as expected. An alternate derivation, using continuous wave functions, rather than discrete states, might seem simpler. However, an electron emitted from the gun of a transmission electron microscope occupies the single state before being diffracted by a crystalline foil, when it adopts discrete Bloch wave states.
, as expected. An alternate derivation, using continuous wave functions, rather than discrete states, might seem simpler. However, an electron emitted from the gun of a transmission electron microscope occupies the single state before being diffracted by a crystalline foil, when it adopts discrete Bloch wave states.
After the transmission, the wave packet is reduced by an exposure event at the resist. While the vertical components of both the group and phase velocities approach c (depending on the potential of the vertical electron microscope gun column), the horizontal component of the phase velocity , when
, when , i.e. in the electron rest frame.
, i.e. in the electron rest frame.
6. Bound States
Equation (4) in electromagnetism and the consequences of Equation (6) represent two results. The wave group is represented graphically in Figure 4 for the context of particle-particle interactions as between electrons in a transmission electron microscope. The wave group due to a travelling particle passes a second bound electron. The group and carrier wave, as drawn, maximize with specific phase relationships as a special case. The group and carrier waves need not be in phase as they pass the bound electron. Meanwhile, in electron beam interactions, fast electrons lose energy to atomic core electrons in specimens. The fast electrons spread in both energy and angle of deflection. The latter is related to momentum distribution of bound electrons in atomic orbits [27] and, with this constraint, scattering is random in individual events. However, the illustration in Figure 4(b), shows how the momentum transferred to the wave group depends on the phase of the bound electron at a given moment of time at the core of the interaction. It appears that the deflection of the fast electron would be predictable, in individual cases at low temperatures, if the relative phases of both electrons were continuous and previously known by a mechanism of entanglement.
7. Conclusion
Computing simulations add clarity to the wave perspective. The phase velocity is measured in electromagnetism, and is known but unmeasurable in particles with mass > 0. If the fact of entanglement at a distance implies incompleteness in quantum theory, then a dependence of mass on relative velocities adds information. Furthermore, when a laser beam is truncated in time, its frequency bandwidth increases and this is consistent with


Figure 4. (Left) Wave group for an incident electron that contains real and imaginary parts within an envelope function. The trajectory is approximately linear. The scattering atomic electron lies on the central horizontal line. The real part of the carrier wave (dark oscillation) is in phase with the peak of the envelope, though this is not necessary. (Right) Phase in a bound state on plane of carrier wave at the moment when the real part at left peaks.
the Uncertainty principle. But the spatial extents of the beams are also truncated along with increases in their respective spreads of momenta. Following Equation (6) the four properties are mutually dependent. This is predicted for free-electron laser beams and for any particle, whether entangled or not. This new continuous wave group describes their evolution in time and space together, whether in vacuo or in dispersive media. The equation applies universally in electromagnetism and likewise in probability amplitudes of free particles.
8. Further Significance
The foundations of quantum mechanics have been discussed by the previous generation of physicists and logicians. There are claims and counter claims regarding circularity in the postulates and in the conclusions of the Copenhagen interpretation. Bohm & Bub, for example, summarized the two basic postulates as [3]:
1) The state of a quantum mechanical system is defined by a continuous single-valued wave function, Y(x,t), which obeys a deterministic equation of motion, Schrodinger’s equation:
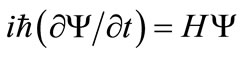 (12)
(12)
2) The wave function determines the probabilities of the possible results of any measurement on the system. Equivalently, the average expectation value for an ensemble of measurements of any observable R is derived from Y through the algorithm:
 (13)
(13)
where 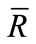 is the operator corresponding to the observable R.”
is the operator corresponding to the observable R.”
This is the interpretation applied in Equation (6). The equation is defined by mean values of frequency and wave vector that are measurable to precisions that depend on the sizes of ensemble samples. It is impossible to prevent science from progressing by selective applications of postulates that are independent of the consistency or completeness of the logic employed. Nevertheless, hidden variables, with hidden constraints, have the potential for transforming probabilistic measurements into those that become determined.
Typically, discussion has taken examples from the measurement of spin and magnetic moment. Typically also, plane waves are employed in the elucidation of theory in diffraction or imaging of particles [28], without detailed complications of wave packets or groups. In this paper we have taken the magnetic part of the wave function to be separable and we leave that topic to a later inclusion of magnetism with the vector potential. Now our concern is with the spatial part. Using Equation (6) we show how the Uncertainty principle can be derived from an elementary treatment that contains hidden variables such as phase velocity and, of course, phase itself. Then the temporal and spatial parts are interdependent even though the operators commute and the variables are independently measurable. We follow multiple commonalities in the theories of optics and electron optics. The model is electromagnetism and Maxwell’s equations, though the probability amplitude in particles is fundamentally and mysteriously different. With the wave group described, Heisenberg’s Uncertainty postulates are written as a theorem in Schroedinger’s interpretation.
NOTES