Stability of Atoms, Causality in Elementary Processes and the mystery of Interference and Hyroscope ()
1. Introduction
In 1909 experimental investigations into scattering of α- particles by a thin layer of matter were made at Rutherford laboratory. The analysis of these experiments allowed Rutherford to conclude that the atom consists of a very small central nucleons surrounded by electrons and most of the atomic mass falls on the nucleus. These experiments also show that the nucleus and electrons are very small as compared to the atom itself. After investigations into scattering of α-particles by nuclei it would be quite natural to compare at atom with Solar system where the nucleus play the part of the Sun and the electrons are like the planets.
These particles move under the action of electrostatic forces, and most of the atom is “empty space”. The size of an atom is determined by the orbit radius of outer electrons
2. Stability of Atoms
Rutherford did not have this work published for two years trying to solve a fundamental difficulty characteristic of the planetary model. The fact is that the atom constructed according to this model can not be stable because the electrons in such an atom must emit energy as classical electromagnetic theory says and fall on the nucleus in a very short time (of 10–9 sec).
Bohr theory allowed more advance. It provided in the first approximation a qualitative explanation for the spectrum of the hydrogen atom and it was a considerable step forward in new ideas. The existence of discrete atomic energy levels is supported by numerous experiments/ Later it was found out that both magnetic fields and nuclear forces form discrete energy levels, too.
The author of one of the previous papers [1] shows that gravity is no exclusion either and any body sets up gravitational energy level around itself. The transition of electrons and protons from one level to another one is followed by discharge of part of the energy in the forms of photons.
Bohr solved the problem of stability of atom by volitional effort assuming that the electron in the ground state of a hydrogen atom does not emit electromagnetic energy in heavy atoms? Where the nuclear charge Z ~ 100, the velocity of the electron on the ground level reaches the velocity of light. Experiments show that on this level, too, the electron has both a kinetic energy and a momentum but any motion of it including vibrational one is characterized by a high acceleration which must inevitably result in photon release and the electron falling on the nucleus. But this not occure and, hence, there should be special reason for which the atom remains stable.
Quantum theory allowed obtaining unique numerical results and predicts new physical phenomena. The euphoria experienced by the young authors of the new theory , including Heisenberg, encouraged them to prove the completeness of quantum theory and the ability of explaining any physical phenomenon within the frame works of this theory. The problem of stability of atom challenged quantum theory, and its authors decided by all means to solve this most difficult problem by forgetting Gödel incompleteness theorem—within the frameworks of any theory there are problems which cannot be solved by this theory.
At first, when Heisenberg developed his quantum theory in the form of matrix mechanics, he completely gave up any visual representations and considered his theory as a computational, purely formal, apparatus. But after getting acquainted with Schrödinger’s works he arrived at the conclusion that a certain visual physical content should be input into the new theory. When interpreting the quantum mechanics it was necessary to analyze the basic concepts of mechanics as applied to microobjects by considering measuring operations, if, for example, we want to define the meaning of the word “coordinate”, we should refer to the experiment which we are going to use to measure it. Heisenberg said that “this word has not any other meaning”. The same refers to other physical concepts and quantities. They are determined by measuring operations.
Analyzing the potentialities of measurements in quantum mechanics unequality Heisenberg gets the important conclusion that two canonically conjugated values cannot be measured at the same time, also he establishes the socalled inequality. It is consistent with the quest for precise knowledge of the relation between theoretical computation and the abilities of experimental check. Later on Heisenberg and Bohr considered a number of imaginary experiments on measurement of canonically conjugated values, coordinates and momenta. This inequality shows that if we, for instance, measure the position of a particle along the X-axis with a certain error (inaccuracy) ΔX and its momentum along the same axis with Δp, the product of these two inaccuracies will be, at least, equal to the Plank’s constant: Δp·Δx ≥ ћ.
Energy and time are canonically conjugated quantities. So, the following unequality ΔE·Δt ≥ ћ/2 is valid for them, too. This relation means that the energy can be determined with the accuracy ΔE in a span of time equal, at least, Δt ~ ћ/ΔE.
Since masses of elementary particles are very small, we cannot observe them without acting on them: measuring means breaking. When analyzing measuring techniques Heisenberg and Bohr draw a conclusion which literally stuns us. In their interpretation followed by most physicists at present there is essential indeterminism, and Heisenberg’s relations will express not only a practical inaccuracy but will be “uncertainty relations”. We shall not have a restriction on the statement that it is impossible to know at the same time the position and the velocity of a particle but it will be stated that a particle, in general, has not simultaneously well-defined position or velocity.
At present Heisenberg’s inequalities are one of the basic statements in quantum mechanics. They can be employed to explain the fact that the electron goes not fall on the atomic nucleus. In a hydrogen atom the uncertainty in determining the position of the electron is similar to dimensions of the atom itself: Δr ~ r.
Therefore, we can not say with certainty in which part of the atom the electron is, let alone speaking about “orbits”.
We can only speak with assurance of the probability p(r)·ΔV of detecting an electron in a volume unit at the distance r from the proton. Quantum mechanics allows in this case calculating the density of probability p(r).
From an excited state the atom can pass spontaneously into lower energy state. The life time of atomic excited state ranges from 10–8 to 10–9 s. The fact that spontaneous transition may occur shows that exited states can not be considered as strictly stationary ones. In this connection the exited state energy is not accurately determined, and the excited energy level has a finite width ΔE ~ 10–8 eV. This value is extremely small as compared with the ionization energy of atom E ~ 10 eV.
The ground state of the atom is stationary, that is, no spontaneous transition into other states from this one is possible. Therefore, the ground state energy can be determined quite accurately. This in its turn, means that in the ground state the electron in a hydrogen atom is at a strictly definite distance from the proton. If the electron could be a little closer to the proton or a little farther from it, this would cause the ground level to be blurred. This conclusion is confirmed by experiments on fine and hyperfine splitting and the Lamb effect. Hyperfine splitting is caused by the interaction between the magnetic momenta of the electron and the proton; as a result, the magnetic energies for every spin state will be slightly different: ΔE ~ 10–5 eV.
If the total spin of the proton and the electron is zero, the electron in this state is a little closer to the proton and this spatial shift is supported experimentally with a high accuracy. In the hydrogen atom in this case two energy levels of the ground state are formed which lie very close together.
Both fine splitting and the Lamb effect demonstrate an exclusive dependence of the level energy on the spatial position of the electron: if the electron slightly approaches the proton, the space immediately reacts to this motion setting up closely-lying energy levels. From this it follows that, if the electron, according to the uncertainty principle, could be with some probability at any distance from the proton, it would to tremendous blurring of the ground energy level ΔF ~ 103 eV which is inconsistent with experiments. We have only to state that quantum theory is unable to solve the problem of atomic stability. This problem is so deep that it cannot be solved without studying the real space structure.
We now turn our attention to Planck’s elementary cell again. In our first paper [1] concerned with the problem of large numbers connected with the intensity relations of Coulomb and gravity interactions. Even 50 years ago both Yukawa and Landau suggested the size of an electron is equal to its Compton length. Experiments show that the larger the mass of an elementary cell, the smaller its size; the limiting mass, mp ~ 10–5 g, corresponds to the volume of an elementary cell Vp ~ 10–99 cm3.
The electron is the biggest of the known elementary particles. Its surface consists of N cells.
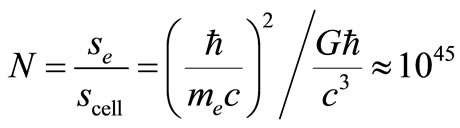
If the electromagnetic interaction intensity was e2/ћc = 1, the size of the hydrogen atom would be equal to that of the electron
re = ћ/mec = 3.86 ´ 10–11 cm
and all the cells of the electron surface would take part in Coulomb interaction at the distance r0 from the proton whereas only one cell would participate in gravity interaction! But the real intensity of Coulomb interaction is 1/α times less than unity and, hence, only N ´ α = 4.17 ´ 1042 cells will take part in Coulomb interaction. Such a macrocell is unable to accommodate an electron. The collectivization effect (the formulation of clasters) referred to in our previous articles can collect a huge amount of elementary cells in one complex, i.e. a macrocell (cluster). An energy level consists of a layer of elementary cells placed between the proton and the electron and incorporating quite a number of macrocells. It is this physical phenomenon that reveals the mystery of squares of natural numbers which are introduced into the solution of Schrödinger equation “manually”.
A more detailed mechanism of energy level formation is considered in the previous papers [1-5]. In my article, about cosmology, we want to show that the formulation of structure, which is the subject of synergetic, occur in the Universe: from elementary particles to cluster of Galactics. The electron is forced to move off the proton at the distance

since only at this minimal distance from the proton the electric charges of these particles are able to from a macrocell with N ~ 1045 cells, i.e. a “Procrustean bed” for the electron.
Granular space theory predicts another wonderful phenomenon: if we try to force the electron closer to the proton, r < r1, opposite charges will be repelled rather than attracted! This phenomenon can be easily checked experimentally as once it was done in experiments by Rhuserford, Jermer or Hofstadter. In this case, however, electrons with energies of 100 eV must act as shells. An experiment with nuclei free of electron shells would be ideal. In this case we could observe a phenomenon similar to the one observed by Rhuserford: in certain cases negative electrons would be scattered by positive nuclei backward with certain energy of incident electrons.
The foregoing considered in the context of real granular space enables us to state that when in the ground state the electron in a hydrogen atom is at a strictly definite distance r neglecting any uncertainty.
As indicated above, the electron in heavy nuclei on the ground level has not only the velocity of light but also a kinetic energy and a momentum which fully rules out atomic stability. How do these two opposites coexist?
In studying granular space of particular importance was the discovery of the physical meaning of velocity: the quantity ν2/c2 is a measure of relative deformation of the space cells surrounding an elementary particle. This discovery solves the problem of atomic stability: when on the ground level an electron is at rest!
In classical mechanics and in quantum theory such quantities as velocity, kinetic energy and momentum are dynamic by character and granular space theory reveals their static character through deformation of elementary cells. Such unusual properties of ordinary things might have been recognized as for back as one hundred years ago because both the electrostatic and the magnetostatic fields proved an absolutely material structure of space.
When on the ground atomic level the electron proves to be in a trap: it cannot either approach the nucleus since repulsion sets in or move away since attraction comes into action.
3. Physical Nature of Spin
When studying the doublet character of alkali metal spectra as well as the abnormal Zeeman effect Pauli in 1924 suggested that they could be explained if certain “twovaluedness” was attributed to the electron, i.e. could be in two states on its orbit. When Kronig become aware of Pauli’s ideas (1924) he proposed that this “two-valuedness” was due to the fact that a moment of momentum equal to ћ/2 and a magnetic moment were to be assigned to the electron. Kronig told Heisenberg about it and the latter got down to calculations at once.
Following Heisenberg we consider the simplest model of electron since we don’t know its inner structure yet; therefore we remove the “two” in the denominator. Then ћ = me·v·re.
At that time Heisenberg could only choose the classical radius r0 as the radius of the electron
r0 = e2/mc2 = 2.8 × 10–13 cm
even though Compton had already his work published where a fundamental physical quantity was introduced— the Compton wave-length 
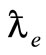 = ћ/mec = 3.86 × 10–11 cm.
= ћ/mec = 3.86 × 10–11 cm.
Using r0 we can estimate the tangential velocity of a point on the equator of a spherical elementary particle, for example, an electron ν ~ 100·c, where c is the velocity of light in vacuum.
On obtaining this result Geisenberg immediately, turned down Kronig’s idea of the intrinsic moment of momentum of electron attributed to the rotation of the electron itself around its axis.
We want to correct Geisenberg’s error since the size of the electron cannot be less than its Compton wavelength, re= . The rotational velocity of electron in this case is equal to the velocity of light ν = c. From the physical point of view this velocity is unacceptable and our attempt to represent visually the particle spin may seem a failure. But let’s consider two experiments. Assume shooting at a target which can rotate around its axis with bullets of a rifled gun. If the target is light it finally begins to rotate in the same direction as the bullets.
. The rotational velocity of electron in this case is equal to the velocity of light ν = c. From the physical point of view this velocity is unacceptable and our attempt to represent visually the particle spin may seem a failure. But let’s consider two experiments. Assume shooting at a target which can rotate around its axis with bullets of a rifled gun. If the target is light it finally begins to rotate in the same direction as the bullets.
In the other experiment we bombard the same light target with polarized electrons. If the beam intensity is sufficient and the target is small enough, it will begin to rotate in a certain time. The same result of these experiments makes us admit that the cause of one and the same phenomenon must be the same; the electron must have a tangential velocity equal to that of light.
And this “Gordian knot” is done by an elementary cell. The electron really offers a tangential velocity equal to that of light but it is not the velocity of electron around its axis. In this case, too, velocity acts as a measure of deformation of the elementary cells making up the electron surface. Let us increase mentally the electron by a huge number of times. We can make out the arrangement of cells resembling rifled bores of a gun. In the case of spin nature demonstrates torsional deformation of the elementary cells on the particle surface, the next statistical quantity—static moment of momentum (angular moment).
And only now we can reveal the mystery of origin of the magnetic field inside the atom: it is static torsional deformation of space cells that we call the magnetic field which completely denies the rotation of the proton around the electron in a hydrogen atom with a huge velocity.
A fundamental specific feature of weak interaction is that weak processes are characterized by mirror asymmetry, i.e. weak interactions do not retain spatial P-parity. The retention of parity must seemingly follow from the fact that there is no mirror symmetry in empty space and vacuum is free of torsional properties.
The cellular structure of space allows solving this mystery as well. As we have, just shown, torsional properties are only inherent in particles at whose formation the cells undergo not only radial but also ordered tangential deformation perceived by us as a spin. As a result of the torsional deformation of the cells forming a particle, at decay of a particle possessing a spin the probability of emergence of a product particle on spin or in the opposite direction are not equal.
As a bullet rotates, every elementary particle comprising the bullet is carried along by kinetic energy; the matter making up this energy deforms space cells causing tangential deformation. The cells forming the electron surface have the same deformation which occurs due to the electron mass at the moment this particle is formed. This deformation of cells simulates a false idea of a rotating electron.
The energy of a particle at rest E = m0c2. What is the role of the quantity c2 in this formula? We again deal here with simulation of the velocity of light due to the deformation of surface cells caused by additional matter—the particle mass.
We have known since school that the gravitational force F = mg.
But looking at an object lying on the table we cannot observe either the velocity or, all the more, the acceleration which this object would possess. In this case, too, the acceleration g makes the deformation gradient of the space elementary cells surrounding this object. The deformation of the cells above the object is larger than that of the cells below it which leads to the concept of force. Surprising, as it may seem, but we observe visually and feel with our hands space cell deformation.
4. God Is Severe but Not Keen
The problem of atomic stability is closely related to the concept of elementary particle trajectory as well as to causality in elementary processes. Peculiar properties of microparticles can be best observed in the following imaginary experiment which idealizes the experiment with electron diffraction from a crystal. Direct a parallel beam of electrons onto an obstacle with two narrow slits (Figure 1(a)) and place a photoplate P behind it. Then close the second slit and perform exposure within the time τ. The blackening on the developed photoplate will be characterized by curve 1 in Figure 1(b). Expose the second photoplate within the same time τ with the first slit closed.
The blackening in this case is illustrated by curve 2 in Figure 1(b). Then expose the third plate within τ with both the slits opened. The blackening is given in Figure 1(c). This pattern is not equivalent to the superposition of the first two curves. It is similar to a pattern made by the interference of two light waves. This patter indicates that both the slits affect the motion of each electron.
Our attempts to understand how an electron reaches one or another point of the screen have led to the pessimistic conclusion that the result obtained cannot be coincident with the concept of electrons along their trajectories. It is asserted that quantum mechanics must be based on concepts of motion materially from those of classical
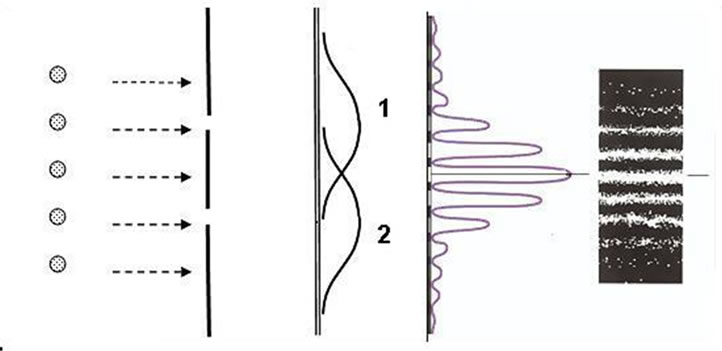 (a) (b) (c)
(a) (b) (c)
Figure 1. Scheme of interference on two slits.
mechanics. In quantum mechanics there is no concept of particle trajectory. And a stronger assertion: simultaneous existence of the coordinates and the velocity at any instant of time would mean the presence of a certain trajectory which the electron does not possess. Thus, in quantum mechanics the coordinates and the velocity of an electron are quantities not existing at the same time. Moreover, it is stated that elementary events in microcosm such as scattering of electrons at diffraction are free of unambiguous causality. In this case, the initial conditions and the causes being the same, the results are different.
A lot of scientists and philosophers including Bohr, Heisenberg, Born, Pauli and Jordan wrote about indeterminism in atomic processes as about an established fact.
But most well—known physicists did not agree with the conclusion about indeterminism in atomic processes. Besides Einstein, Planck, Schrödinger, de Broigleand quite a number of other scientists and philosophers were against this conclusion, too. Langevin argued against indeterminism and called the reasoning about abandoning as “intellectual lechery”.
Now we can say that Winer was right by stating that “quantum physics is concerned just with rather rough manifestations of events which are characterized by much a finer time and space structures”.
So, in our experiment we could observe diffraction from two slits but we cannot say through which of them the electron passes. Such diffraction can take place only when the electron passes through both the slits and the question through which of the slits it passes has no sense. Most of the scientists today agree with this conclusion.
According to Bohr, corpuscular-wave dualism is caused by the fact that micro object itself is not either a wave or a particle in the ordinary sense.
Once Feynman wrote [6]: “I am going to consider only an experiment with two slits which is specially conceived so that it could cover all the mysteries of quantum mechanics and bring you and all the paradoxes, secrets and strange things of nature together by all 100 percent. If you can, do not torment yourself over the question “How can it be?” or otherwise you will reach a deadlock from which nobody has got out yet. Nobody knows how it can be!”
Einstein, Lorentz, Plank, de Broil based their theory on the representation of so-called hidden parameters, i.e. on the existence of physical quantities relating to the particles or to other, still unknown, micro objects whose behavior unambiguously determines the behavior of the electron or another similar physical object.
Since this experiment can be explained only with the use of interference, we are going to try to find it in a granular space structure.
A very important case of interference can be observed in the superposition of two counter-running plane waives with the same amplitude. The resultant vibrational process is called a standing wave. In practice standing waves arise when waves are reflected from obstacles. When the incident wave and the reflected wave running to meet it are superimposed, they form a standing wave. So, we have the following equations for two plane counter-running waves:
A1 = acos(ωt – kx)
A2 = acos(ωt + kx).
Combining both the equations and transforming the result by the formula for cosine sum we get:
A = A1 + A2 = 2acoskx·cosωt
By replacing the wave number k by its value 2π/λ we can get for A:
A = (2acos2πx/λ)·cosωt (1)
Equation (1) is valid for a standing wave where the amplitude depends on x:
Amplitude = [2acos2πk/λ]
At the points, where 2πx/λ = ± πn (n = 0, 1, 2, ···), the amplitude of vibrations gains its maximum value 2a whereas the intensity equals 4a. These points are called crests of a standing wave.
Granular space theory considers a moving particle to be not “a wave-particle centour” but “a rider on a horse”. “Rider” means the electron and “horse” means the space cells deformed by kinetic energy. The pulsating motion of this matter form a cell deformation wave and serves as a basis for introducing such wave characteristics as amplitude and phase. It is very important to note that all the electrons which have reached the slit are characterised by different wave phases and, hence, we would never observe even two similar particles.
Since this cell deformation wave runs ahead of the electron, near the slit it exates the standing wave of space cell deformation between two slits. The length of this standing wave λ is naturally equal to the electron wave length, but the velocity of this wave is equal to the velocity of light. And while the electron passes through the slit, a standing wave can be formed. The second slit in this case serves as a node of the standing wave.
For further study of this phenomenon we should take into account Huygens principle used in studing light refraction on the boundary of two media. Huygens proposed a wave theory which considers light to be an elastic wave propagating in space ether. Today we do not need ether because its role is played by material space which serves as an absolute reference system. While the cell deformation wave is travelling a distance d from slit 2 to slit 1, the spherical wave is able to travel a distance Δ around slit 2.
Huygens principle says that cells deformation between slits can be considered as a set of secondary waves. A wave front can be obtained by drawing an envelope of secondary waves (Figure 2).
A decisive role in choosing the direction of further electron motion is played by the discreteness of cell deformation peaks for a standing wave. This discreteness also dictates the discreteness the distance Δ: Δ = kλ, (k = 0, 1, 2, ···).
From a right triangle we have Δ = d·sinα. From this we can get a condition for the peaks of electron flux level
d∙sinα = k (k = 0, 1, 2, ···) (2)
Now, it is clear, why formula (2) describes the experiment correctly even, though, the original hypothesis is wrong.
It is easy to calculate the electron wave phase φ:
φ = 2πd·sinα/λ
Finally, the intensity of diffracted electron beam
I = 4I0(x,α)·cos2(sinα·2πd/λ)
where I0 is the intensity for one slit.
In studies of this physical phenomenon we do not dot our “i’s” and cross our “t’s” because more detailed investigations are required. We have, however, found a source of electron interference, and this is a standing wave of elementary cell deformation.
Besides, space itself, i.e. its structure is the hidden parameter our great predecessors used to speak about. The study of this wonderful physical phenomenon has demonstrated again that Einstein was right in his argument with Bohr when he said that “God does not play dice”. The interaction of the standing wave with the electron wave is responsible for the only trajectory along which the electron moves after passing through the slit.
5. The Mystery of Hyroscope
People have known the whipping top, a simple children’s toy, for a long time. And everybody who first touches it, is surprised with its unusual behaviour. Let us consider the motion of a hyroscope (Figure 3) one end of which is fixed at the point P on another vertical axis.
Assume that the hyroscope is a rotating wheel with weightless spokes, with the radius r and mass m. The

Figure 2. Passage of an electron through a slit.
gravity moment about the point P is
M = m·g·R
and is perpendicular to the angular momentum L of a rotating wheel:
L = m·r·v
Uniform precession is described as a partial solution of equations of motion and can be observed only if the hyroscope is triggered properly. When we hold the hyroscope by its axis so that it cannot presses (but continues to rotate), it is acted upon by no moments of forces, even the gravity. This drop does not surprise us because everybody knows that all bodies fall on the Earth. At the same time the wheel begins to move aside. How it happen that the down-directed directed force makes the hyroscope move aside. Modern theory makes use of the conception of a moment of forces in this case. Since the hyroscope drops, it rotates thus setting up a momentum of forces. This imparts motion to the hyroscope axis around a vertical axis, that is, causes precession. But the most interesting thing is not in precession but, despite the action of huge mass of Earth, the hyroscope stops falling down. Moreover, soon the axis begins to rise to the original level! As a result, the end of the axis describes a cycloid. These oscillations are called nutation.
Under the action of the moment of force M the angular momentum L of hyroscope gets an increment
dL = Mdt
within the time dt which coincides in direction with the vector M, that is, is perpendicular to L. The precession angular velocity is evidently equal to
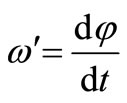
where dφ is the turning angle of the plane passing through the axis of the wheel and the hyroscope

Hense:  and
and  where L = I·ω, I is the momentum of wheel inertia.
where L = I·ω, I is the momentum of wheel inertia.
I = m·r2.
The precession angular velocity
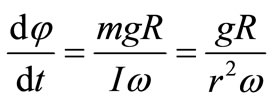 (3)
(3)
The velocity ω does not depend on the wheel mass. It may be one kilogram, one ton, or one thousand tons. But, despite of such a colossal weight, the wheel can swarm above the Earth causing real amazement since none of the formulas in the world, similar to (3), can explain what force holds the hyroscope suspended.
To reveal this mystery let us change the formula (3) introducing the linear velocity of precession V' = ω'·R From this we have 2m·ω·v'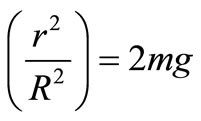
The quantity 2m·[ω·v'] is the Coriolis force upwarddirected, r2/R2 is the geometrical factor.
The nature of Coriolis force, the inertial force, the centrifugal force and others, however, is not understood yet. The absence of any body which would cause these forces makes most physicists call them “fictitious” because of their feebleness to understand the nature of these forces.
It is quite evident that it is space that can help us! But amorphous boiling vacuum that constantly forms virtual particles and disturbes the laws of conservation of energy, momentum and moment of momentum cannot produce a huge force upward-directed and applied to a wheel. Only space with a rigid material structure and high elasticity is able to withstand gravity.
It is the structure of such space that can be studied using the theory of granular space, so let us consider this structure.
Now, let us perform an imaginary experiment and assume that we are able to identify the elementary cell of 10–33 cm. First, we closely observe the initial falling of the wheel. Let the wheel rotate counter-clockwise (proper motion). If we look at the wheel from the moment L, we can see that for the particles of the wheel on its left half the speeds of falling and rotation are summed but on the opposite (right) side they are subtracted. But the speed here is the degree of cell deformation and, hence, the cell deformation is more on the left than on the right. And again a gradient of cell deformation appears, the wheel begins to precess couter-clock wise. If we change the direction of proper rotation (clockwise), the precession will change its direction for the same reason.
Now we change the condition of the experiment. We stop the proper motion of the wheel and then let it go again. The wheel simply falls down and there is no any precession. But a gravity moment appears in this case too! Where has it gone?
The effect of nutation calls for some energy or addition mass. From where does the wheel get this additional mass? Let us observe the beginning of falling. We have already considered the appearance of additional mass when a body moves in a gravitational field: space redistributes the matter of the destroyed particles. The interference of two rotations of the wheel transports this mass thus setting up precession.
Now let us consider the particles in the upper and lower parts of the wheel. It can be seen that the particles down take part in two motions where the speeds have the same direction, whereas for the upper particles they are subtracted. So we can observe downward-directed deformation gradient of the space cells surrounding the wheel. It is just the miraculous force which holds the suspended and even lifts it.
The mystery of hyroscope has been discussed at last but it is not only mystery. The terminology of physicists will loose notion “fictitious” forces as all the forces in nature are real. As we have stressed several times in our papers, any force appears when the deformation of space cells on opposite sides of the body is different and this sets up a deformation gradient. This fact certainly confirms the hypothesis that v²/c² is the relative deformation of cells.
In [1] we clarified that electron surface consists of clasters, each of them containing 4.17 × 1042 cells, which make Coulomb and gravity forces very different. Similar clasterization occurs in the hyroscope thus setting up a Coriolis force.
Three solid axis characterizing hyroscope (in our case they are mutually perpendicular) give decisive evidence that our space is three-dimentional which rules out an attempt of performing additional space measurements.
The fundamental aim of scientific knowledge is to express the whole complexity of nature through the simplest concepts. We wish to understand something real and clear up the meaning of this reality rather than to be able just to manipulate formulas and correctly predict experimental results.
In such a complicated problem as the interactions of elementary particles it is sometimes helpful to reconsider so-called “habitual” views and get rid of the long-established dogmas.
All the “seeming” (reversed effective forces) have a specific feature: they exist only on the boundary of rotational bodies or bodies moving along a straight line; being local forces they instantly disappear beyond the bodies. Such forces drastically differ from Coulomb and gravity forces.
The deformation of space sells and gradient of this deformation unravel the secret of following striking phenomenon: the hyroscope wheel is stable even when its axis holds a horizontal position.
6. Conclusions
The body of mathematics of quantum mechanics was created very quickly. But large extent it was elaborated using quesswork, rather logically unrigorous analogies, ets. And even though this body has been applied with success and allowed solving many problems in atomic physics, the physical meaning of this new theory seemed unclear and contradictory.
Bohr, Heisenberg, Born, Pauli and Dirac put forward their own interpretation of quantum mechanics. It was based indeterminacy, complementarity, indetermenism and probability.
Einstein, Plank, Schrõdinger, Lorentz, Langevin and many others were against such treatment of microcosm physics.
At the International congress of 1927 almost all delegates were unanimous.
In one thing by ruling out the principle of indeterminacy, indeterminism and statistics they insisted on the following physics must remain on the position of “reality”. Even the smallest part of the Uniiverse must be as objective as a town or a stone, no matter whether it is accessible for observation or not. They believe that there should be on the concepts of existence of physical quantities relating to particles or physical quantities relating to particles or to some other. Still unknown, microobjects whose actions unambiguously determine the behaviour of an electron or another similar object. In this letter to Born on April 29, 1922 Einstein again and again turns back to the problem of determination of physical phenomena it is intolerable for him to think that an electron under the action of a beam can freely choose the time and the direction of its further motion.
For objectivity, it should be accepted that there are no contradictions in quantum theory itself, they only arise when physicists want to minimize Gëdel theorem of incompleteness and explain the physical phenomena beyond this theory. Quantum theory does not deal either with the space structure or structure of elementary particles, including the concept of quarks. The present-day quantum theory is a look at the microcosm from “a bird’s-eye view”.
Three fundamental problems of microcosm have proved to be a stumbling block for quantum theory. They are: atom stability, the spin structure of elementary particles, and diffraction of protons and electrons.
An electron in heavy atoms, when being on the ground level, has extremely accurate numerical values of both its velocity, almost equal to that of light, and a huge kinetic energy and momentum. But it cannot either move along a complicated trajectory or jump from place to place. The numerical values of the physical quantities characterizing the electron are accurately proved by a lot of experiments. The situation is quite paradoxical and the solution of this problem with the present-day quantum theory is paradoxical, too: the absolute definiteness of the position of en electron in an atom on the ground level must be explained by full uncertainty of this position using Geisenberg inequalities for solving this problem.
According to Geisenberg’s work, we can conclude that to measure means to violate. One can not measure accurately the momentum and the position of a particle at a time.
However, “thanks to Bohr” the treatment of the problem is quite different: a particle, in general, cannot have any well-defined position or velocity at a time.
Thus, Geisenberg’s inequalities have made us speak about them more than they would like to speak themselves, and nearly mystical by nature.
As for the structure of granular space, the theory reveals at last the physical meaning of v2/c2 as a relative measure of space cell deformation and cuts the Gordian knot tied round atom stability when on the ground energy level, an electron is at rest!
The experiments on electron diffraction have provided the basis for conclusion that the principle of causality in these experiments seems to be violated, since under similar causes the consequences in this case are different. This statement is contrary to fact.
Each electron, as it approaches one of the slits, differs from the others in that the deformation of elementary particles making the essence of “the pseudophoton,” which carries away the electron, may be as large as one cell to the wavelength λ. This deformation initiates the deformation of the space cells between two slits of the standing wave.
Therein lies the exceptional role of the second slit. The interaction of a standing wave with the electron wave determines the only trajectory for every electron along which it will travel after passing through the slit. This fully agrees with Einstein’s standpoint.
The children’s toy “waving top” have provoked curiosity of people for several thousand of years. The revolving toy can not fall under Earth’s attraction. Only the studies into the real structure of space have make it possible to reveal this mystery.
Some more words about the problem of causality. Let us choose at random any elementary cell and observe its state. It is ease to verify that our cell will begin to get deformed only when its direct neighbors act on it. Deformation cannot jump over pieces of space which establishes absolute causality of all events in the Universe as well as the ultimate velocity of transformation of information and interactions.
In the last years of his life Dirak, one of the founders of quantum mechanics, who supported Bohr’s standpoint said that he was ready to give up any postulate of quantum theory in exchange for determinism, Schrõdinger was in despair to say that if he had known the result of publication of his theory he would never have put it forward.
In 1926 Born suggested probabilistic treatment of Ψ- function. In his opinion a wave function is not a real physical field but has a probability meaning like the distribution function used in statistical physics. Statistical interpretation of wave function suggested by Born became universally accepted soon.
The past millenniums show us that probability has always been a payment for our not knowing the real processes taking place in a certain physical event or because of great number of particles participating in this event.
The theory of granular space enables revealing the real physical meaning of |Ψ|2—the density of the space cells deformation.
7. Acknowledgements
I would like to thank V. Kubik for valuable discussions.