1. Introduction
The edge coloring problem finds a partition of all the edges in a graph into a collection of subsets of edges such that, for each subset in the partition, no edges share a common vertex. Here the objective is to minimize the number of subsets in a partition. This problem has interesting real life applications in the optimization and the network design, such as the file transfers in computer networks [1]. For the file transfer problem in computer networks, each computer x has a limited number f(x) of communication ports. For each pair of computers there are a number of files which are transferred between the pair of computers. In such a situation the problem is how to schedule the file transfers so as to minimize the total time for the overall transfer process. The file transfer problem in which each file has the same length can be formulated as an edge coloring [1]. The problem can be generalized to require the subsets to have other properties. In this work, we are interested in the partition of edges into the subsets such that each covers all the vertices. The objective, instead, is to maximize the number of such subsets.
Our terminology and notation will be standard. The reader is referred to [2] for the undefined terms. Graphs in this paper are simple, unless otherwise stated, i.e., they have no loops or multiple edges. We use V(G) and E(G) to denote, respectively, the vertex set and edge set of a graph G. A k-edge coloring 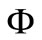 of a graph G is an assignment of k colors
of a graph G is an assignment of k colors  to the edges of G. The coloring
to the edges of G. The coloring  is proper if no two adjacent edges have the same color. Unless otherwise stated, the edge coloring of graphs in this paper are not necessarily proper. An edge cover of G is a subset S of E(G) that saturates each vertex of G, i.e., each vertex of G is an end vertex of an edge in S. An edge cover coloring of G is an edge coloring such that the edges assigned the same color formed an edge cover of G. Clearly, the edge cover coloring may not be proper. The edge cover chromatic number
is proper if no two adjacent edges have the same color. Unless otherwise stated, the edge coloring of graphs in this paper are not necessarily proper. An edge cover of G is a subset S of E(G) that saturates each vertex of G, i.e., each vertex of G is an end vertex of an edge in S. An edge cover coloring of G is an edge coloring such that the edges assigned the same color formed an edge cover of G. Clearly, the edge cover coloring may not be proper. The edge cover chromatic number  of G is the maximum size of a partition of E(G) into edge covers of G. G is said to be k-edge cover colorable if there is an edge cover coloring of G with k colors. An important theorem of Gupta [3] states that
of G is the maximum size of a partition of E(G) into edge covers of G. G is said to be k-edge cover colorable if there is an edge cover coloring of G with k colors. An important theorem of Gupta [3] states that
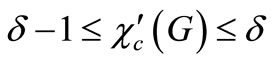
From the above result, we can see that the edge cover chromatic number of any graph must be equal to  or
or , This immediately gives us a simple way of classifying graphs into two types according to
, This immediately gives us a simple way of classifying graphs into two types according to . More precisely, we say that G is of CI class if
. More precisely, we say that G is of CI class if , and that G is of CII class if
, and that G is of CII class if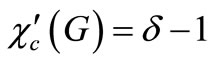 . Wang and Liu discuss the classification problem of nearly bipartite graphs and gave some sufficient conditions for a nearly bipartite graph G to be of CI-class [4]. Xu and Liu considered the edge cover chromatic number of multigraphs [5]. Hilton generalized the edge cover coloring and obtained many interesting results, the following theorem can be found in [6].
. Wang and Liu discuss the classification problem of nearly bipartite graphs and gave some sufficient conditions for a nearly bipartite graph G to be of CI-class [4]. Xu and Liu considered the edge cover chromatic number of multigraphs [5]. Hilton generalized the edge cover coloring and obtained many interesting results, the following theorem can be found in [6].
Theorem 1.1. If G is a bipartite multigraph, then G has a k-edge coloring such that the number of distinct colors represented at v is min  for each
for each .
.
By Theorem 1.1, for any bipartite graph G with minimum degree , it must have a
, it must have a  -edge cover coloring. So, we can see that all bipartite graphs are of CI class. In this paper, we discuss the classification problem on double graph of some graphs, and a good algorithm for edge cover coloring on double graph of k-regular graph can be obtained by the proof of theorem.
-edge cover coloring. So, we can see that all bipartite graphs are of CI class. In this paper, we discuss the classification problem on double graph of some graphs, and a good algorithm for edge cover coloring on double graph of k-regular graph can be obtained by the proof of theorem.
2. The Classification of Double Graph
Let  be a copy of simple graph G. Let ui be the vertex of G, and vi be the vertex of
be a copy of simple graph G. Let ui be the vertex of G, and vi be the vertex of  correspond with ui. A new graph, denoted by D(G) is called the double graph of G if
correspond with ui. A new graph, denoted by D(G) is called the double graph of G if 

It is easy to see that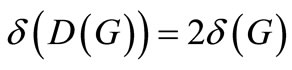 , and we have the following result.
, and we have the following result.
Theorem 2.1. Let G be a graph of CI class, then D(G) is also a graph of CI class.
Proof. It’s enough to give a  -edge cover coloring of D(G) with the color set
-edge cover coloring of D(G) with the color set .
.
Since G is of CI class, G has a  -edge cover coloring, and we can also give a same
-edge cover coloring, and we can also give a same  -edge cover coloring of
-edge cover coloring of 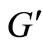 with the color set
with the color set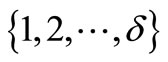 . Next, we color the edges between the vertices of G and
. Next, we color the edges between the vertices of G and .
.
Let , the induced subgraph of D(G) by
, the induced subgraph of D(G) by , denoted by
, denoted by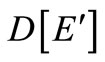 . It must be a bipartite graph. By Theorem 1.1,
. It must be a bipartite graph. By Theorem 1.1,  has a
has a  -edge cover coloring with color set
-edge cover coloring with color set . Clearly, we give an edge coloring of D(G) such that each color of
. Clearly, we give an edge coloring of D(G) such that each color of  appears at least once at each vertex
appears at least once at each vertex  . That is, D(G) has a
. That is, D(G) has a 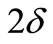 -edge cover coloring. This proves the Theorem.
-edge cover coloring. This proves the Theorem.
By Theorem 2.1, for each CI class graph G, D(G) is also of CI class. Now we consider that if G is of CII class, what about D(G)? This question seems very difficult to answer in the current, but we can study some special CII class graphs. We have known that some regular graphs are of CI class and some regular graphs are of CII class [7]. It is well known that the Petersen graph P is of CII class, but its double graph D(P) is of CI class. For all k-regular graph, we have the following result.
Theorem 2.2. Let G be a k-regular graph, then the double graph D(G) is of CI class.
In order to prove Theorem 2.2, we need the following useful lemma.
Lemma 2.3. Let H be a 2k-regular graph, then H contains k edge-disjoint spanning 2-factors , and
, and .
.
Proof. Let , Since H is a 2kregular graph, it must be an Euler graph. Let T be an Euler tour of H. Now, we conform a bipartite graph
, Since H is a 2kregular graph, it must be an Euler graph. Let T be an Euler tour of H. Now, we conform a bipartite graph  by T. Let
by T. Let ,
, .
.
The vertex 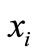 and
and 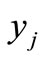 are adjacent in
are adjacent in  if and only if
if and only if  and
and  are adjacent sequentially in T. Clearly,
are adjacent sequentially in T. Clearly,  must be a k-regular bipartite graph. By theorem 1.1,
must be a k-regular bipartite graph. By theorem 1.1, 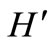 has k edge-disjoint perfect matches
has k edge-disjoint perfect matches . We notice that each perfect match
. We notice that each perfect match  in
in  is exact a spanning 2-factor of H. Then H contains k edge-disjoint spanning 2-factors
is exact a spanning 2-factor of H. Then H contains k edge-disjoint spanning 2-factors , and we have
, and we have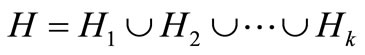 . The lemma is true.
. The lemma is true.
The Proof of Theorem 2.2. Since G is a k-regular graph, the double graph D(G) is a 2k-regular graph. By Lemma 2.3, D(G) contains k edge-disjoint spanning 2-factors , and
, and  . We notice that the order of D(G) is even, then each of
. We notice that the order of D(G) is even, then each of  is an even cycle. By Theorem 1.1, for
is an even cycle. By Theorem 1.1, for ,
,  has 2-edge cover coloring with color set
has 2-edge cover coloring with color set . So, we give a 2k-edge cover coloring of D(G) with color set
. So, we give a 2k-edge cover coloring of D(G) with color set .
.
This proves the Theorem.
3. Remarks and Discussion
It is easy to see that a polynomial time algorithm for edge cover coloring of the double graph of any regular graph can be obtained by our proof. But in general, the problem of determining the edge cover chromatic number of any graphs is NP-hard because deciding whether a 3-connected 3-regular graph G is proper 3-edge colorable is NP-complete [8], which is the special case of our general problem. On the other hand, for each CII class graph G it is not known whether determining the classification of its double graph D(G) is NP-hard. But we have the following conjecture.
Conjecture 3.1. Let G be a graph of CII class, then D(G) must be a graph of CI class.
It is seems very difficult to prove the above conjecture, but one can prove that the conjecture is true for some special CII class graphs.
NOTES