The Economics of Power Generation Technology Choice and Investment Timing in the Presence of Policy Uncertainty ()
1. Introduction
In economics, accurately predicting market outcomes as well as assessing the dynamics of affecting policies, is a notoriously difficult and complex task. The interaction of countless firms and individuals, all with different characteristics and subject to various policies, creates future market situations that are complicated to predict but nevertheless important to assess. The power sector is not exception to this and is currently also undergoing major restructuring. It is not only subject to market uncertainties (e.g., fuel prices) but also governed by a number of international and national policies (e.g., emission allowance schemes, green certificate schemes and permitting processes). Many of these policies are explicitly designed to stimulate emission reductions as well as investments in renewable energy sources. Even so, they may also introduce additional uncertainties in terms of the timing and choice of technology for investments. For instance, how will the European Union Emissions Trading Scheme (EU ETS) change in the future; will new sectors be included and will the allocation system be reformed? These types of uncertainties are important to assess for investors in the power sector, but it is equally important for policymakers to understand that the uncertainties associated with new policy might drive the power sector in an unintentional direction.
The purpose of this study is to analyze how market and policy uncertainties affect the timing and choice of technology for new investments in the Swedish power sector. In order to achieve this objective, we develop an investment model that incorporates uncertainty in the form of stochastic prices. This model permits an assessment of the economics of power generation technology and how it is affected by moving from a deterministic to a stochastic investment environment.
The presence of uncertainties of future returns and costs are amongst the more critical factors affecting the willingness to invest. There is however little consensus in the economic literature on how and to what extent policy uncertainty connected to carbon pricing specifically (e.g., emissions trading schemes) will affect investment behavior in the power sector (e.g., [1-5]) suggests that climate policy will not add any significant uncertainties for electricity investors in the future, and even stimulate firms’ investment incentives, at least if the policy is consistent over a longer time period. The main obstacle for investtors is instead the fuel price. Other studies point out that the set-up of an emission allowance scheme (allocation and allowance prices) could affect fuel prices, which in turn could decrease investments in various technologies (e.g., gas-fired power as pointed out in Laurikka and Koljonen [1]. Thus, it is important to analyze how the implementation of a specific policy affects the behavior of the investor.
The remainder of this paper is organized as follows: Section 2 provides a review of previous studies that have dealt with market and policy uncertainties in the electric power sector. Section 3 outlines the investment model used in this paper as well as the data needed to implement the model empirically. Section 4 presents the results from the model simulations, while section 5 concludes the analysis.
2. A brief Review of Previous Research
Economic theory predicts that spot market pricing, such as Nord Pool, is a sufficient condition for an efficient level of investments. Caramanis et al. [6,7] conclude that optimal spot pricing always give higher welfare than regulated prices, and that spot prices should provide sufficient incentives for investments. Still, uncertainties about future price levels and policies may reduce the investment incentives (e.g., [8]). Within this context, Green and Newberry [9] analyze the British market; Borenstein et al. [10] the Californian market; and Garcia-Diaz and Marin-Uribe [11] the Spanish market. However, these studies mostly focus on short-term supply and inadequately address longterm issues. A serious limitation of adopting a short-run perspective is that capacity is determined exogenously. A long-run perspective is used by von der Fehr and Harbord [12] and Castro-Rodriguez et al. [13]. The results from these studies support the notion that spot pricing in power markets is important. In addition, von der Fehr and Harbord [12] suggest that investment incentives and the level of investments are directly dependent on how prices are determined. In general, the price determination and its development, together with the market structure, are important variables for understanding the level and the timing of investments as well as the choice of technology.
Other than the price signal, important investment determinants are policies and regulations1. Policies affecting investments in renewable energy are analyzed by Bird et al. [14]. Even though it is difficult to pinpoint the exact drivers, the authors suggest that investment in wind power in the USA is driven by favorable policies and a growing market. In Europe, favorable investment conditions can be found through schemes that aim at promoting renewable alternatives such as the German feed-in tariffs, the UK Renewable Obligation, and the Swedish green certificate scheme. It is, however, important to keep in mind that there are significant barriers to entry in the power market and that policy and regulations affect also these barriers. For instance, the power market is characterized by high capital costs of constructing a competitive plant, long lead-time to bring the plant in operation and sometimes long site approval processes for certain renewable technologies [15,16]. There is an ongoing scientific discussion in the economic literature on how a market should be designed in order to promote investments (e.g., [17]). For instance, Takizawa and Suzuki [18] analyze investments in the power sector in a regulated market and conclude that the possibilities to invest are better when the electricity price is regulated, at least for projects requiring large capital investments per unit of output such as wind power. Then again, a deregulated market could result in a higher market price, but the higher price is necessary for investments to take place [19,20].
It is possible to distinguish between “ordinary” market uncertainties and uncertainties that are induced by policies. Market and other external uncertainties such as fluctuations in fuel prices and reservoir levels can to some degree be perceived as easier to manage than the uncertainties that stem from various policies. In this paper we classify market uncertainties are fuel prices and the electricity price while non-market uncertainties are modeled through permit and green certificate prices. It should be noted that the permit and certificate prices are set on markets but the policy-makers can affect the market prices by e.g., adjusting the cap, changing the number of permits issued, changing the distribution or changing the quota obligation. Even though policymakers could affect the permit and certificate markets, the time-frame has proven to be important when it comes to how firms perceive stability and certainty. Furthermore, there exists a relationship between the certificate scheme and the EU ETS. For example, if the price of permits increases at the same time as the marginal power in the Nordic electricity system is fossil fuel-based, the electricity price will increase. A higher electricity price would stimulate investments in renewable power by itself and thus reduce the investment effect of the certificate system. With higher electricity price the certificate price that is needed to reach the quota for renewable production becomes lower. Nordleden [21] analyses the driving forces for investments in the energy market in Sweden. They found that one of the crucial variables is policy stability since fluctuations in policies reduce the investment incentives. In the absence of policy stability the uncertainty increases and thereby also the cost for the investment since a higher uncertainty requires a higher rate-of-return requirement for the investment to take place.
3. Investment Model for Power Generation
In modeling investment decisions under uncertainty we follow the seminal work of Dixit and Pindyck [22], and acknowledge three general investment characteristics that can be identified for the power sector. Firstly, investments are partially or completely irreversible and once made the capital cost can be considered sunk. Secondly, uncertainty is always present for future returns and costs. Thirdly, the investment can take place at flexible timing. That is, the investment can take place today if the returns are expected to be high enough to recover all the costs or it can be postponed in order to get better information. The investors have the opportunity or option but not the obligation to invest in a project in a specific time period. In addition to the characteristics mentioned above, several different technologies can be used to generate power, thus making the investment decision depend on the available technologies and their associated uncertainties [23].
Before proceeding, it should be noted that the model developed is related to real-option models used for studying the electricity sector. However, we are not interested in explicitly deriving any option values that an investor might face. Instead, we focus on the technology choice and investment timing of investments in the power sector and how they are affected by policy and market uncertainties. Uncertainty in the power sector propelled by market conditions and climate policy has been modeled before (e.g., [1,24-28]). While these studies analyze power markets in general and how they are affected by uncertainties, our approach focuses more specifically on the Swedish power market and its characteristics.
The investment model outlined below is similar to Roques et al. [29] in that we assume that investment decisions are made in five year intervals. This assumption makes the model more tractable and reflects the usually long lead-times associated with large investments. In order to calculate and compare various investment options we first consider the net cash flow (NCF) associated with a given investment as in Equation (1)
 (1)
(1)
where TR and VC are total revenues and total variable costs, respectively, for time period t (t = 0,∙∙∙,T) and technology i (i = gas, wind, bioenergy). We consider the choice between three technologies: natural gas, bio-power and offshore wind. Offshore wind power instead of onshore wind power is chosen in order to permit a comparison of future investments of similar size and due to the favorable potential for offshore investments in Sweden [30]. The three power generation technologies represent the likely new investment choices presently available during the coming 20 years in Sweden [31]. Other investment options, such as capacity expansions of existing nuclear and hydropower plants, are not included. Even though it has been possible to increase the capacity of existing nuclear and hydro plants, continuous capacity expansions in the future are unlikely since the existing plants approach the end of their lifetimes.
The variable costs are a function of several economic variables as described in Equation (2).
 (2)
(2)
where  is the price of input fuels such as gas or biomass,
is the price of input fuels such as gas or biomass,  is the EU ETS permit price,
is the EU ETS permit price,  the cost for emitting NOX gases, and
the cost for emitting NOX gases, and 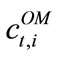 represents the operation and maintenance costs. We include the fee for NOX emissions that is applicable for both power and combined heat and power generators using natural gas and biofuel as inputs. For wind power, the only variable cost is
represents the operation and maintenance costs. We include the fee for NOX emissions that is applicable for both power and combined heat and power generators using natural gas and biofuel as inputs. For wind power, the only variable cost is . The total revenues can be expressed as:
. The total revenues can be expressed as:
 (3)
(3)
which is composed of electricity sales , heat sales
, heat sales  (for combined heat and power stations) and, in the case of bio power and wind power, the green certificate revenues
(for combined heat and power stations) and, in the case of bio power and wind power, the green certificate revenues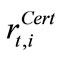 . The technology-specific revenues from electricity, heat and certificate sales are calculated as:
. The technology-specific revenues from electricity, heat and certificate sales are calculated as:
 (4)
(4)
where 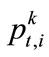 is the price for electricity, heat and certificates,
is the price for electricity, heat and certificates,  is the capacity and
is the capacity and  is the maximum annual utilization of the plant.
is the maximum annual utilization of the plant.
Some of the revenues and costs are in various degrees treated as stochastic. Following the costs and revenues associated with an investment, the technology and timing decision is based on the net present value (NPV) per unit of output and is calculated as:
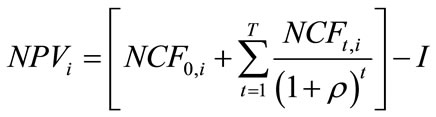 (5)
(5)
where I is the investment cost and ρ is the discount rate. The expression in Equation (5) does not explicitly address any aspects of uncertainty; instead uncertainty enters the model through the future development of prices.
The model structure is a general description of the costs and revenues facing new investments. However, in order to assess the investment timing and technology choices in the presence of price uncertainties additional assumptions are needed. For this reason, by comparing the results from two different simulations we can illustrate how uncertainties affect investment timing and technology choices:
• Simulation 1: First-best investment. Investments are made in the first time period where NPVi > 0.
• Simulation 2: Optimal investment timing. Investments are made in the time period with the highest NPVi > 0.
Let us start by considering simulation 1. If the NPV for all technologies is negative in the first period another evaluation takes place in the next time period. If a positive NPV never occurs it is assumed that no investment is done. This approach results, foremost, in an instant technology choice pattern, but, it can not be used to find the optimal investment timing. Figure 1 depicts how decisions and technology choices are made under simulation 1 using 5-year intervals.
In simulation 2 we search for the most profitable time period to invest in, and also what technology that is best to invest in given that investments can be made throughout the entire time frame. Specifically, we search for the maximum NPV for all technologies in all time periods. In other words, the investment takes place in the time period and in the technology that has the highest positive NPV so that:
 (6)
(6)
In this simulation we are interested in when the most favorable condition occurs and how the corresponding technology choices are influenced by uncertainties.
4. Modeling the Presence of Investment Uncertainties
In order to address the uncertainties associated with future prices a stochastic process is used for the electricity, fuel, carbon permits and certificate prices. The stochastic process is assumed to be one-factor mean reverting (sometimes referred to as Ornstein-Uhlenbeck process) except for the certificate price, ; the latter modeled as an independent random variable which is log-normally distributed with a mean of SEK 205 and a standard deviation of SEK 10. These numbers have been derived from the historical certificate price data. The mean reverting assumption is supported by several studies that suggest that long-run commodity prices exhibit a mean-reverting behavior (e.g., [32-34]). Furthermore, several studies have used a mean-reverting process when analyzing the electricity market [24-26,32,35,36]. However, there are studies suggesting other stochastic processes, especially when modeling electricity prices. For instance, Fleten et al. [37] argue that a geometric Brownian motion (GBM) is more suitable for modeling short-term fluctuations but, as Laurikka [24] suggests, mean reverting processes yield a more conservative value than other processes where the probability distributions are wider. In this case, as the interest is not in short-term price fluctuations, a mean-reverting process is chosen. This implies that prices (x) can be modeled as:
; the latter modeled as an independent random variable which is log-normally distributed with a mean of SEK 205 and a standard deviation of SEK 10. These numbers have been derived from the historical certificate price data. The mean reverting assumption is supported by several studies that suggest that long-run commodity prices exhibit a mean-reverting behavior (e.g., [32-34]). Furthermore, several studies have used a mean-reverting process when analyzing the electricity market [24-26,32,35,36]. However, there are studies suggesting other stochastic processes, especially when modeling electricity prices. For instance, Fleten et al. [37] argue that a geometric Brownian motion (GBM) is more suitable for modeling short-term fluctuations but, as Laurikka [24] suggests, mean reverting processes yield a more conservative value than other processes where the probability distributions are wider. In this case, as the interest is not in short-term price fluctuations, a mean-reverting process is chosen. This implies that prices (x) can be modeled as:
 (7)
(7)
where η is the speed of reversion, x* the long-run mean – or the “normal” – value of x, σ the variance and ε a random normally distributed variable. The parameters η,  and σ have been estimated through regression analyses based on historical market prices. The parameters used for the mean reverting stochastic processes are presented in Table 1.
and σ have been estimated through regression analyses based on historical market prices. The parameters used for the mean reverting stochastic processes are presented in Table 1.
The long-run mean in the stochastic process mimics a business-as-usual case, that is, it reflects the situation with “normal” price movements. Other movements that are due to external events (e.g., political instabilities in oil-producing countries) are reflected in the movements of the stochastic process. Figure 2 exemplifies sample paths for the electricity price and includes the long-run mean x* and a high and a low electricity price sample path.

Figure 1. Technology choices in simulation 1.

Figure 2. Sample paths for the simulated electricity price.
We use the stochastic prices in a probabilistic setting and simulate several price paths that are used to construct probability distributions for the technology-specific NPVs. This allows us to assess the investment returns when prices are both at a low and a high level, and the technology that yields the highest returns given our two alternative model simulations.
5. Data Inputs
Technology-specific costs and technical parameter assumptions for the different technologies are presented in Table 2. All prices used in the simulations are in SEK (2005 value)2. The technology data concern commercially available alternatives in Sweden and includes: a 400 MW CCGT power plant, a 80 MW biomass CHP plant, and a park of 30 offshore windmills with a total generation capacity of 90 MW. Availability means annual utilization of the plant measured in hours. The revenues from selling heat are computed assuming a heat price of SEK 320,000 per installed MW. The effects of different climate and energy policies currently in place in Sweden are modeled in two ways; permit pricing through EU ETS (for fossil fuel-based power generation) and green certificates (for renewable energy)3.

Table 2. Technology-specific costs and technical parameters.
6. Results
The model is run 60,000 times for the stochastic variables and the corresponding NPVs, something which yields various probability distributions for the different NPVs. Such Monte Carlo simulation models have proven to be useful when evaluating technology choices with various uncertainties in the electricity sector [41-44]. Furthermore, the simulations are done using different discount rates, ranging from 5 to 15 percent, thus representing different rate-of-return requirements.
We start by presenting the results from simulation 1. Figure 3 summarizes the distribution of chosen technologies in different time periods using a discount rate of ten percent. The pie charts represent the technology choices that are made in each period and the results indicate that in 88 percent of the simulations a positive investment decision is made in the first time period, predominantly in bio-power. In 9 percent of the simulations no investment at all takes place. The small share of investments that are made in later time periods are evenly distributed between the time periods τ + 10, τ + 15 and τ + 20. Surprisingly, no investment occurs in time period τ + 5. This can, at least partly, be explained by the fact that the majority of the investments have been made in the first time period even though it could be better (more profitable) to invest in a later time period. If we consider the resulting technology choices in the time periods following the first, the technology distributions are in general the same. The results indicate that the bio-power option is the most profitable regardless of whether the investment is made in the first or last time period. Both windand bio-power investments are positively affected by the green certificate scheme increasing the revenue side of the net cash flow, thus increasing the probability of yielding an overall positive NPV. However, bio-power also produces significant amounts of heat that makes it a more attractive investment choice compared to wind. Then again, wind power is not affected by stochastic fuel prices like gasand bio-power, something which increases the uncertainty for the latter technologies.

Figure 3. Technology choices in simulation 1 (10 percent discount rate).
The results for simulation 2 are presented in Figure 4 and suggest that the chosen timing of investments is more evenly distributed across the time periods compared to the outcome in simulation 1. Overall, this suggests that forcing electricity companies to invest early imposes an economic cost; postponing investments is often a profitably strategy. Compared to the results from simulation 1, the investments are overall more profitable in the last time period (τ + 20) instead of the first. Figure 4 indicates that in 34 percent of the simulations the investment is more likely to occur in the last time period compared to 23, 12, 11 and 11 percent in the time periods τ, τ + 5, τ + 10 and τ + 15, respectively. In 9 percent of the simulations no investment at all occurs. Similar to simulation 1, the most attractive technology is bio-power which is the chosen technology in around 60 percent of the cases regardless of investment timing.
In addition, concerning the chosen technology the following pattern can be observed: 1) the likelihood of wind power being chosen decreases over time and 2) the likelihood of gas power being chosen increases over time, whilst the choice of bio-power remains fairly stable. One explanation for gas being chosen more frequently over time is that in some late time periods, gas investors face situations with relatively high electricity prices in combination with low permit and fuel prices. In a similar fashion, over time wind investors end up in a situation where low levels of the stochastic output prices cannot be compensated from fluctuations in other prices. The results depend thus on how sensitive each technology is for revenue volatility, and gas-fired power has the most to gain from flexible investment timing opportunities. As we approach the end of the planning horizon, the advantage of wind having less volatile revenues diminishes, at the same time as the waiting option for gas power is less exercised and that investment option is chosen more frequently. This implies that the waiting option increases the distribution of the investment timing, i.e., there is a wider spread of investments seen over the whole planning horizon under simulation 2 compared to simulation 1. The results suggest that it may be optimal to postpone an investment depending on the development of the stochastic variables because of the value of information about future profitability gained by waiting. In addition, the relative higher capital requirements for wind in comparison with gas power also propel wind power to be chosen less frequently over time.
When it comes to the effect of the EU ETS and the green certificate scheme, the results suggest that the relative competitiveness of gas and biomass changes, making biomass a more attractive investment option. Since biomass can be considered a carbon neutral fuel, the permit system stimulates more investments in biomass at the expense of gas. However, the improved competitiveness of biomass will most likely change its long term price trend reducing the effect of the permit system. Furthermore, Laurikka and Koljonen [1] argue that the permit system can cause a pressure to modify existing energy

Figure 4. Optimal investment timing and technology choices in simulation 2 (10 percent discount rate).
taxes, an action that also might reduce the effect of the relative competitiveness between gas and biomass. The dominant choice of technology early on is biomass followed closely by wind power. As time passes, gas power increases its attractiveness whilst wind power becomes less attractive. Overall, the presence of stochastic prices does not promote wind power as much as could have been expected.
7. Sensitivity Analysis
Two major drivers of the results can be identified; the discount rate and the parameter values in the stochastic processes. In traditional investment analysis where deterministic NPV calculations are used, uncertainties are captured in the discount rate. In order to account for uncertainties not explicitly modeled, various discount rates are tested. By applying different discount rates to the two simulations we can test how sensitive the results are to various rate-of-return requirements. The results from simulation 1 using a reduced discount rate (ρ = 0.05) suggest that roughly all investment occur in the first time period, distributed between bio-power (69 percent) and wind power (31 percent). No gas power projects are initiated. With a higher discount rate (ρ = 0.15) the investment timing changes and it is distributed across several time periods. In addition, it is more likely that no investment at all occurs due to the higher rate-of-return requirement. There is a 50 percent chance that the investment occurs in the first time period and a 34 percent chance that no investment at all occurs. The remaining investment probabilities are distributed between the τ + 10, τ + 15 and τ + 20 with 8, 4 and 3 percent probabilities, respectively. The choice of technology also changes with a higher discount rate. In this case the most likely technology is gas power (approximately 62 percent) followed by bio-power (approximately 35 percent) and wind power (approximately 3 percent). This distribution of technology choice holds for every time period except the first in which gas power has 88, bio-power 12 percent and no investments in wind power occur. When the rate-of-return requirement increases wind power looses competitive ground due to the relatively high capital costs.
The results from simulation 2 using the same variation in the discount rate suggest that the likelihood for an investment to occur is more evenly distributed across the time periods as well as over the different technologies. With a five percent discount rate most of the investments occur in either time period τ or in time period τ + 20. There is roughly a ten percent probability that the investment occurs in either of the periods τ + 5, τ + 10 and τ + 15, respectively. The choice of technology is similar to the results using simulation 1 (with 5 percent discount rate) in that bio-power and wind power are the dominating technology choices. However, in the first time period wind power is the preferred technology and as time passes the choice of bio-power increases. The use of a higher discount rate indicates a tendency for late investments, if any investment at all occurs. Furthermore, the preferred technology has switched from bio to gas power being the dominating choice of technology.
The choice of wind power increases with a lower discount rate, since it has a higher capital requirement per unit of output. Changing the discount rate reveals the sensitivity of the results. Not surprisingly, using a higher discount rate suggests that it is more likely that the investment will not take place and if it occurs it is more likely that the chosen technology is gas power instead of bio-power that was the dominating technology using a 10 percent discount rate. Using a lower discount rate still suggests that bio-power is the most profitable technology.
The assumptions made for the stochastic processes are also assessed. In order to analyze the robustness of the model, the mean-reverting process has been replaced with a Geometric Brownian Motion process and the estimated NPVs became relatively similar. More interesting is to assess how different parameters in the mean-reverting process would change the result. Consider, for instance, the volatility parameter (σ). If a higher volatility is chosen the variance on the stochastic variables would increase but most likely not change the relative merits of the chosen technologies. Analogously, a higher start-up price (x0) would not alter the relative merits of the technologies since the estimated price series applies for all technologies simultaneously. However, if the stochastic parameters for the permit price are changed the competitive position between gas and the renewable alternatives would change.
8. Conclusions
The purpose of this paper has been to analyze how uncertainties affect investments in the power sector with a focus on technology choice and timing. The developed model explains the investment pattern and the flexibility of investment timing when the power generators face uncertainties expressed in input and output prices. For large-scale new investments in power generation, we have analyzed the impact of stochastic electricity prices, input prices on the investment decision problem considering the joint determination of technology choice and investment timing. Thus, for policy making, our model suggests that the interrelation between policy measures and uncertainties should be taken into account for at least two reasons: 1) policies could directly affect the electricity price and thus increase the level of uncertainties and 2) they could affect the input price, changing the optimal choice of technology.
The results indicate favorable economics for bio-power in Sweden. These results are foremost driven by the certificate scheme, EU ETS and the expected operational lifetime of the various power plant technologies, and also since bio-power gains from heat sales. It is though worth noting that the Swedish climate polices are not explicitly designed to promote any specific technology.
Investment timing and technology choice are of principal interest to not only policy-makers but also to the various market participants. Due to the non-storage characteristics of electricity, investments are crucial in order to balance supply with future demand expectations and its timing can therefore strongly affect the electricity price. Furthermore, there exist a limited number of alternative technologies available for power generation. In Sweden, for which the model is applied, there is a prohibition to invest in large-scale hydro and nuclear power reducing the available technologies to wind-, gasand bio-power. This might force power generators to invest in more expensive technologies that require higher electricity prices in order to make them financially attractive. Each technology is associated with different cost structures and uncertainties in input prices and policy formulations, which together with the irreversibility of the investment affect the optimal timing of investments.
The results in this paper are similar to, for instance, Fuss et al. [26] who analyzed how investments in coalbased power and carbon capture and storage (CCS) technologies are affected by policyand market-based uncertainties. Their results suggest that uncertainty—up to a certain degree—could be benign for investments in carbon capture technologies but that uncertainty beyond a certain threshold serves as a driver for investors to postpone environmental friendly investments. Investors simply wait and accumulate information on the final governmental decision about climate policy. As a consequence, climate policies might indirectly put an upward pressure on the electricity price through the absence of investments in the power sector. This could furthermore cause a situation where power generators and investors respond to uncertain policy by investing in existing capacity and prolonging the lifetime of the existing plants [45].
Finally, there is a higher probability for investments in renewable energy power to be made in later time periods. By increasing the quota obligation in the Swedish green certificate scheme, the Government can stimulate investtors to invest early, and this would work in favor of reaching the goal of 17 TWh of renewable power capacity in 2016. However, increasing the quota obligation also increases the electricity price and thus the overall cost that could cause a lower acceptance for long-term policies in the power industry.
9. Acknowledgements
We thank Bio4Energy, a strategic research environment appointed by the Swedish government, for supporting this work. We also gratefully acknowledge financial support from Vattenfall Nordic Generation AB as well as comments from Patrik Söderholm, Magnus Sjöström, Mats Nilsson, Christopher Gilbert, John Tilton and David Maddison.
NOTES
2EUR 1 corresponds roughly to SEK 9.
3Bio-fuelled power is assumed to be carbon-free since the net effect from the corresponding CO2 emissions is zero since the biomass used for combustion sequestrates emissions in its growing phase and offsets any future emissions.