Efficient Hardware/Software Implementation of LPC Algorithm in Speech Coding Applications ()
1. Introduction
Applications such as cell phones, hearing aids, and digital audio devices are applications with stringent constraints such as area, speed and power consumption. These complex applications can be well addressed by Systems on Programmable Chip (SoPC). Modern Field Programmable Gate Arrays (FPGAs) contain many resources that support DSP applications such as embedded multipliers, Multiply Accumulate (MAC) units and processor cores. The motivation for the introduction of such processor core comes from the idea that most FPGAs contained within an embedded system require interaction level with an external processor. Moving this processor onto the chip allows the FPGA and the processor to communicate without the bottlenecks associated to communicating with off-chip devices. Several programmable logic manufacturers offer FPGAs platform. Altera, Atmel, Xilinx [1] propose devices that integrate hardware cores of processors such as ARM, MIPS and PowerPC CPUs and/ or allow instantiation of soft processor such as MicroBlaze from xilinx and Nios from Altera, DSP and microcontroller cores like PicoBlaze. In this work, we propose different implementation modes of the Linear Predictive Coding (LPC) algorithm used in the majority of voice decoding standard. According to its criticality of the LPC algorithm and its reusability property, the windowing/autocorrelation bloc seems a good candidate for IP design. This block is thus implemented by three different versions on an FPGA. The system performances have been evaluated with a prototyping board integrating embedded Microblaze processor with peripherals on a FPGA Spartan 3. This flexible system enables to reduce overall product cost, achieve target performances, eliminate risk of obsolescence and finally use industry standard software development [2]. Pure software implementation of the LPC is first proposed using MicroBlaze soft core RISC processor. Second pure hardware architecture is implemented using VHDL description. Finally, the autocorrelation core is then proposed to be implemented using HW/SW architecture with the existing processor. Each architecture performances are compared for different data lengths. The remainder of this paper is organized as follows: Section 2 gives a necessary background on the LPC analysis and the autocorrelation algorithm. The starter board and implementation tools are detailed in Section 3. Section 4 introduces the Microblaze processor. Each architecture implementation details are depicted in Section 5. Section 6 presents the implementation results. Finally Section 7 concludes the paper and details some future works.
2. LPC Algorithm Overview
The LPC algorithm is a widely used technique for voice coder. In fact the human speech is produced in the vocal tract as a combination of vocal cords (in glottis) interacting with articulators. Actually, it can be modeled by the passage of an excitation signal through a filter. This model called linear predictive coding (LPC) is given in the case of an auto-regressive signal [3,4] and is presented in Figure 1(a).
The correspondence between the real world and the mathematical models is given in Figure 1(b) [5,6], This is equivalent to say that the input-output relationship of the filter is given by:
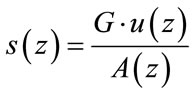 (1)
(1)
In order to evaluate the LPC model, the linear regression has to be solved, that is to say the coefficients a(i) of the recursive filter are to be found. If the operations involved by the LPC analysis are summed-up, this task includes five sub-tasks:
• A windowing + an autocorrelation• The Levinson Durbin algorithm [7,8]• A LP to LSP Conversion [9,10]• A LSP Quantization [11]Interpolation & conversion of the LSP coefficients.
3. Implementation Approach
In order to extract an efficient hardware/software partitioning, the processing and communication complexity of the LPC algorithm was evaluated in [12]. A survey of the distribution of the different processing complexity parts of the algorithm is necessary. The aim is to first know to what extent it can be interesting to achieve some blocks into hardware rather than software and, secondly, if this blocks can be used in other applications in order to justify their specification as a reusable component.
3.1. Hardware/Software Partitions
The windowing/autocorrelation block and the LSP Quantization block are the most critical blocks. The technique used for the quantization is specific to the standard G729. In fact the LSP coefficients are quantized using the LSF (line spectral frequency) representation in the normalized frequency domain (0, π). Then the quantization is achieved using a two-stage vector quantizer [13]. In fact, rather than doing the computations, most voice coder use a simple look-up table. This solution can be efficiently implemented into software. This is the way we have implemented this block. The other significant sub-block, the autocorrelation sub-block, is data computation dominated. We thus decided to centres round this block. In fact the critical operations of the majority of digital signal processing algorithms are usually the convolution or product accumulations. A dedicated arithmetic unit achieving a multiplication and accumulation is generally used to cope with this problem; it is called a MAC.
To achieve our objectives, we have used the Spartan™-
3 Starter Kit provided by Xilinx [2].
3.2. Board and Embedded Processor
The Spartan-3 Starter Board from Xilinx provides a powerful, self-contained development platform for designs. It features a 200 K gate Spartan-3, on-board I/O devices, and one MicroBlaze fast asynchronous SRAM, making it the perfect platform to experiment with any new design, from a simple logic circuit to an embedded processor core. The board also contains a Platform Flash JTAGprogrammable ROM, so designs can easily be made nonvolatile. The Spartan-3 Starter Board is fully compatible with all versions of the Xilinx ISE tools. It ships with a power supply and a programming cable, so designs can be implemented immediately with no hidden costs.
Figure 2 shows the Spartan-3 Starter Kit board, the main components and features are quoted below:
• 200,000-gate Xilinx Spartan-3 XC3S200 FPGA;
• 1M-byte of Fast Asynchronous SRAM;
• 3-bit, 8-color VGA display port;
• 9-pin RS-232 Serial Port;
• PS/2-style mouse/keyboard port;
• Four-character, seven-segment LED display;
• Eight slide switches;
• Eight individual LED outputs;
• Four momentary-contact push button switches.
The implementation of our system will be carried out using XPS tool (Xilinx Platform Studio) provided by EDK [14] environment (Embedded Development Kits) as well as the Core Generator tools included in ISE (integrated software environment), to profit from Xilinx IP [15] respecting the constraint of time to market (TTM).
The Spartan 3 starter kit which combines XC3S200 of Spartan 3 FPGA family, provides an environment for designing an embedded and reconfigurable system based on the MicroBlaze softcore processor.
The MicroBlaze embedded soft core is a Reduced Instruction Set Computer (RISC) optimized for implementation in Xilinx FPGAs. With few exceptions, the MicroBlaze can issue a new instruction every cycle, maintaining single-cycle throughput under most circumstances. Unlike any other hard processors which are actually implemented in the FPGA at a transistor level, the soft core is an IP block written in HDL and is implemented in the free resources of an FPGA. Therefore it is configurable by choosing the components that would be included in the system.
According to the application type, MicroBlaze processor can be configured in several ways to save power or area. MicroBlaze processor provides four bus connections, namely the Local Memory Bus (LMB), the Onchip Peripheral Bus (OPB), the Fast Simplex Link (FSL) and the Xilinx Cachelink (XCL). The LMB is a dedicated bus for MicroBlaze and on-chip block RAM connection. The OPB is a CoreConnect IBM standard bus [16] and gives the capability to connect variety of available IP blocks and peripherals.
The FSL has a FIFO-based interface and it provides a connection between a custom hardware to assist particular application. Lastly the XCL interface provides a link between MicroBlaze processor and data and instruction caches.
4. Solution Space Exploration
The LPC block input is assumed to be a 16 bits PCM signal. Two pre-processing functions are applied before the encoding process signal scaling, and high-pass filtering. The scaling consists of dividing the input by a factor 2 to reduce the possibility of overflows in the fixed-point implementation. The high-pass filter serves as a precaution against undesired low-frequency components. A second order pole/zero filter with a cut-off frequency of 140 Hz is used.
The Linear Prediction (LP) is performed once per speech frame using the autocorrelation method with a 30 ms asymmetric window. Every 80 samples (10 ms), the autocorrelation coefficients of windowed speech are computed and converted to the LP coefficients using the Levinson algorithm.
The LP analysis window consists of two parts: the first part is half a Hamming window and the second part is a quarter of a cosine function cycle. The window is given by:
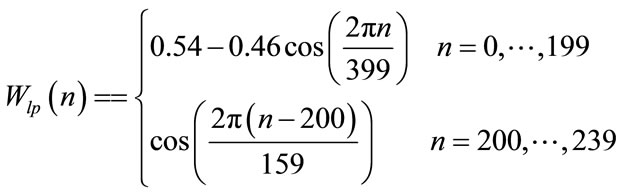 (2)
(2)
The windowed speech is given by the following equation:
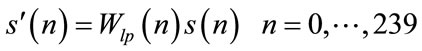 (3)
(3)
and is used to compute the autocorrelation coefficients as follow:
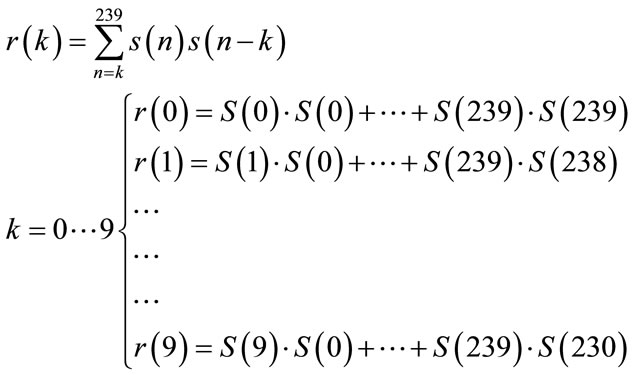
4.1. Software Solution
In software version, LPC Algorithm is a full software implementation mapped onto the MicroBlaze processor. Data is accessed through the data cache and comes from the external SRAM.
The system architecture of a MicroBlaze implementation is shown in Figure 3. The LPC algorithm is recoded in ANSI C and stored in on-chip BRAM. The size of BRAM is set to 64 K which is the maximum size that one MicroBlaze processor can have on the Spartan-3 XC3S200 [2] FPGA.
The connection between Block RAM and MicroBlaze processor is through ILMB [15] (Instruction-side Local Memory Bus) and DLMB [15] (Data-side Local Memory Bus). The DOPB [15] (Data-side Onchip Peripheral Bus) is used for connecting the following peripherals:
UART [15], OPB Timer [14], and Debug Module [15]. The HyperTerminal is a communication program used on a PC workstation to print the result received at PC’s serial port. The Xilinx Microprocessor Debug (XMD) tool of Xilinx Embedded Development Kit (EDK) is used to debug the system from the PC workstation. The elapsed-time of running the C program in the Block RAM presented later is achieved by starting and stopping the OPB Timer peripheral before and after a specific code segment. Execution time results for each partition are summarized in Table 1.
4.2. Hardware Solution
The second architecture is a pure hardware implementation of the algorithm. This architecture makes use of an autocorrelation core that will be presented later in HW/ SW architecture section. It also makes use of a windowing core in order to reduce the generation of side lobes in the frequency spectrum. To be done two blocks are implemented: multiplier block and a 256 word 16 bit ROM as shown in Figure 4.
To minimize development time Xilinx’s CORE generator has been used to produce the simple arithmetic operators and memory required by this windowing block.
The used ROM is constructed in the Spartan III FPGA using the ISE’s CORE generator. In fact the CORE generator can be used to produce devices ranging in complexity from simple arithmetic operators and delay elements to complex building-blocks such as digital signal decoders, processing filters, multiplexers, transformers, FIFOs, and memories.
The content of this memory is defined by supplying an input coefficient precalculated starting from the Equation (2).
The final system is built around the windowing core and the autocorrelation computation presented in section II.B. Figure 5 summarizes the global hardware system design. Table 2 presents execution time for each block.
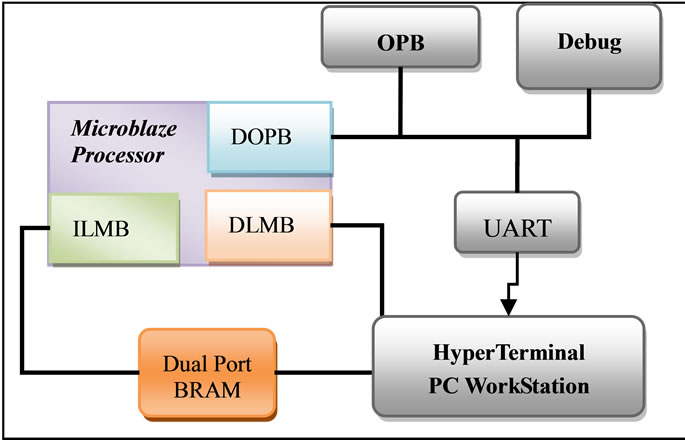
Figure 3. Microblaze system architecture.
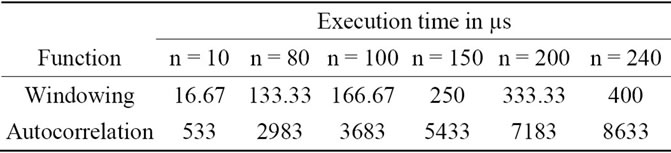
Table 1. Profiling results with pure software.
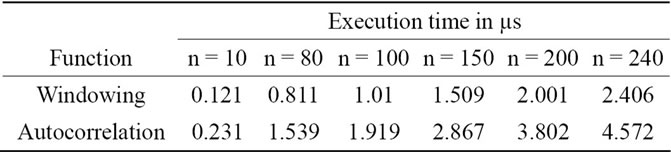
Table 2. Profiling results with pure hardware implementation.
This global design is implemented using the Spartan 3 Xilinx board. The RTL specification is made compatible with most of FPGA design tools for an efficient component reuse. This is also the reason why we have used handwritten RTL MAC rather than on-chip one.
The specification can be parameterized according to the window size and the data width (word length). It is also parameterized according to the value of index k of the r(k) autocorrelation coefficient equation.
4.3. Hardware/Software Implementation
In this version, we proposed a HW/SW high-performance implementation. As shown in software version, profiling algorithm shows that the autocorrelation could be implemented into hardware block. Thus we have applied an EDK based design flow for the implementation of the windowing/autocorrelation algorithm. In fact The EDK is an integrated environment for HW & SW co-design.
One of the biggest challenges of this architecture was to get a System On a Programmable Chip (SOPC) with LPC algorithm. This means implementing both software and hardware components. As the target device, a Spartan-3 starter kit was chosen due to its flexibility, great promise of integrating both the hardware and software co-designs into one flow as shown in Figure 6.
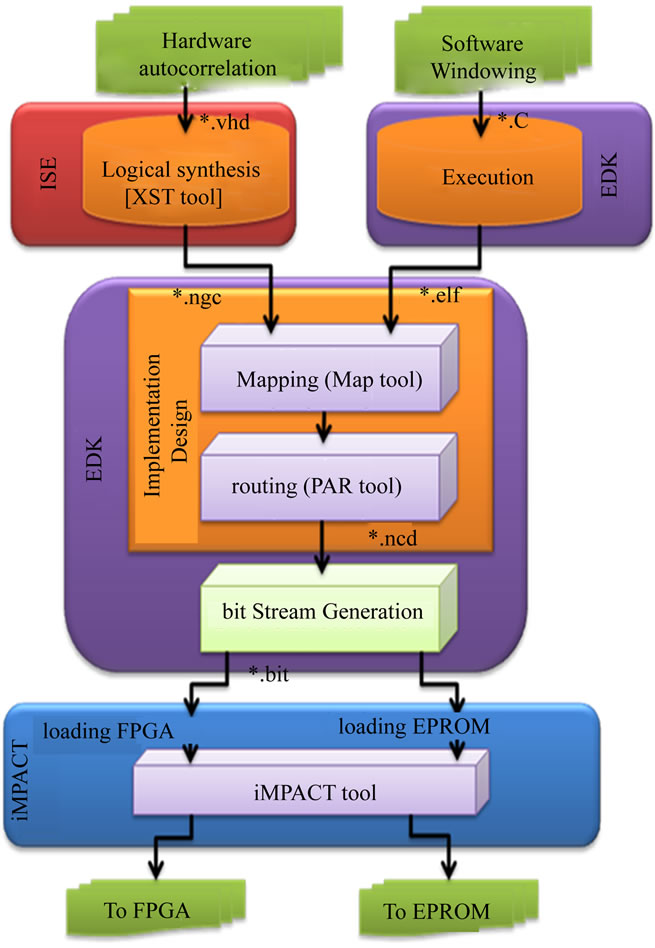
Figure 6. Embedded development tool flow overview.
The soft core Processor MicroBlaze is used in a standalone mode to run a software program (written in C) which is loaded into BRAM.
The whole design flow, except the simulation execution, is covered by Xilinx EDK and ISE software packages. The Adding a Processor System to and FPGA Design module introduces the two design flows of a hardware system available in EDK: the XPS flow and the ISE flow. The procedure involved in each flow is illustrated Figure 7. This flow summarizes our system design. The speech signal is stored in the SRAM. The MicroBlaze processor achieves the windowing computation then sends the results to the Autocorrelation hard Block to compute the autocorrelation coefficients.
In this architecture the user logic is an Autocorrelation core which is coded in VHDL. It should be noted that linear prediction in speech processing has an important characteristic since it is determinist. Taking this characteristic into account it is usually possible to apply some parallelism techniques in order to increase the performance of the implementation.
The Microblaze achieves the windowing computation then sends the result to the user logic. The FPGA computes the autocorrelation coefficients.
In our case the autocorrelation computation can be split in many sub-tasks independently executable since the set of computations can be written as in Equation (4).
Systolic arrays are very well suited to compute this kind of computation [17]. Applying the dependence method [18], a linear systolic array (Figure 8) has been specifically designed for the autocorrelation computation with 10 MAC-based cells as described in Figure 9. For a clock cycle i, every MAC(k) reads S(i) and S(i – k) and adds to its previous result S(i) * S(i – k). At the first clock edge MAC0 performs the multiplication S(0)·S(0). At the second one, MAC0 performs S(0)·S(0) + S(1)·S(1), and MAC1 performs the multiplication S(1)·S(0). At the third clock edge MAC0 performs S(0)·S(0) + S(1)·S(1) + S(2)·S(2), MAC1 S(1)·S(0) + S(2)·S(1) and MAC2 S(2)·S(0), and so on.
Finally, the ten autocorrelation coefficients r(0)…r(9) are provided after 240 clock periods.
This linear array achieves an efficient speed-area trade off with a parallelism rate of 10 (10 useful multiplications and accumulations each clock cycle on average). A single clock is used to control this array. Furthermore, since this systolic array is linear (one dimensional array), the data communication interface is also easy to be (re) used.
Systolic arrays are very interesting for reusable components. This kind of array uses elementary cells locally interconnected and is basically regular.
That allows the design of soft IPs (according to the VSIA taxonomy [19]) with a generic parameter repre-
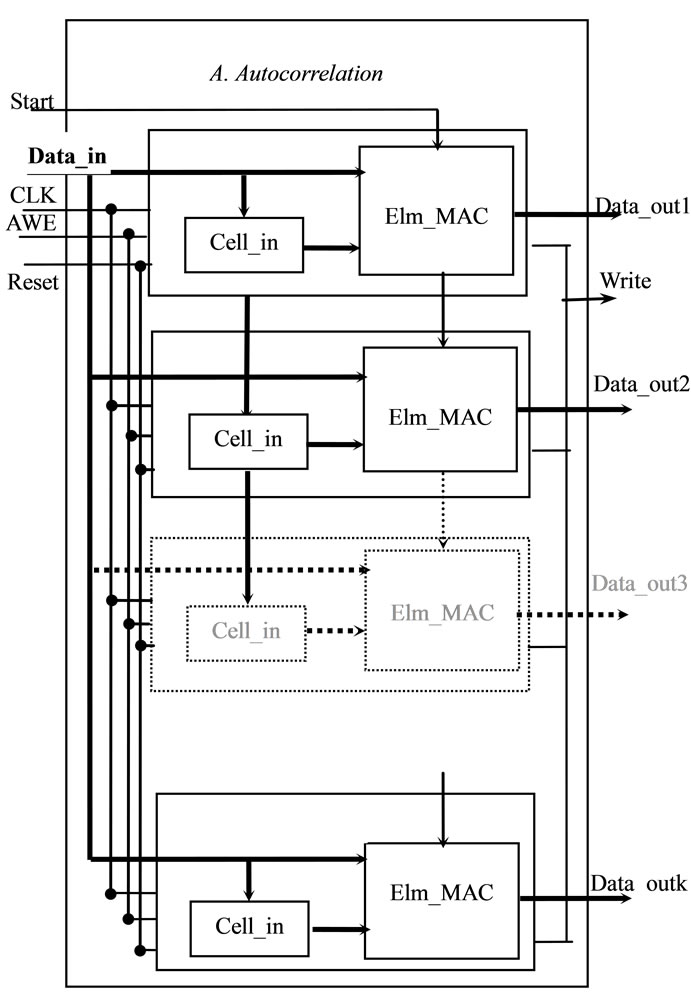
Figure 8. Linear systolic array for the autocorrelation.
senting the number of elementary cells. In our case, this parameter corresponds to the index k of the autocorrela-
tion coefficient equation r(k).
The size of the proposed array (number of MAC cells) does not depend on the maximum value of the n index: this value only sets the number of input data, i.e. it sets the size of the hamming window. The proposed array can thus be easily used in many speech coders (GSM 160, G723, G729 240, etc.) [13,20].
Another interesting point of this autocorrelation implementation is that it doesn’t need intermediate data to be stored in a RAM. Additional memory accesses and control are thus avoided.
The profiling of the HW/SW architecture is shown in Table 3. It can be seen that the gain in execution time is considerable as soon as the number of samples increases. In fact the autocorrelation core reduces the execution time by a ratio close to 96%.
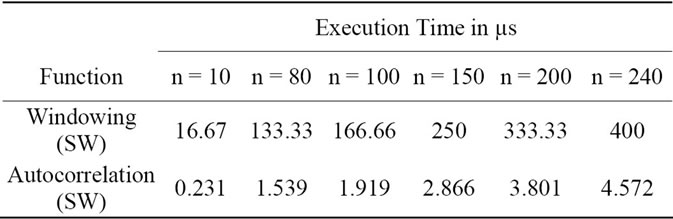
Table 3. Profiling results after using hardware accelerator.
5. Results and Discussions
In this paper, three different architectures were proposed for realizing a windowing and autocorrelation computation. These three architectures are implemented on Spartan-3 board.
Using a window sized of 240 and a word length of 16 bits, the profiling results of each architecture are shown in Figure 10. It is clear that the pure hardware implementation results in a significant speedup over the software implementation and rather HW/SW version.
The hardware resources for the implementation are summarized in Figure 11. The SW architecture resource requirements are fixed with the value of n all versions of the algorithm are implemented in software and changing n requires just modifying the C code and recompiling it. We note that the hardware version, use more silicon surface then HW/SW version and then over consumption.

Figure 10. Profiling results for different architectures.
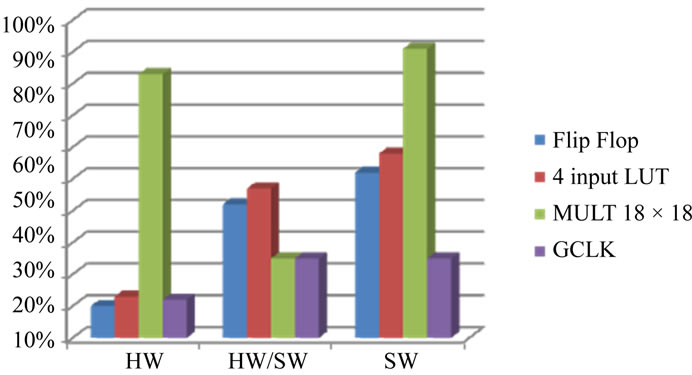
Figure 11. Resource utilization for different architectures.
The results show that the increased hardware resource requirements are not excessive when compared to the basic MicroBlaze core.
6. Conclusions and Future Works
In this paper three different architectures were proposed to implement the LPC algorithm. All of them are aimed for voice decoding process using the Xilinx board based MicoBlaze soft processor. A comparison between the three architectures shows that using a hardware architecture coupled with a MicroBlaze processor in mixed architecture reduces the number of cycles required to perform the most critical operation by about 96%.
Also, the HW/SW approach allows the designer to focus only on the development of the VHDL core description without taking into account communication problems. This goal is reached due to the definition of an automated flow IP-Cores integration into a complete system architecture without requiring the user interaction. Using a HW/SW architecture gives a significant speed up results with a moderate area and lower flexibility. Thus, such a design will enable us to achieve an optimum tradeoff between speed and flexibility permitting to make a complete system on programmable chip (SoPC). In fact the proposed approach represents a general computing model which can be extended too many different applications like G729 coder.