Environmental Policies and Firm Behavior with Endogenous Investment in R & D ()
This paper investigates upon the optimal amount of oil usage in an economy characterized by competitive firms and by a monopolistic innovator. It is close in spirit to Denicolo 1999 and Parry 2003. There are two alternative oil saving technologies: the conventional one is promptly available to firms while the advanced one, providing more efficiency in oil saving, must be paid to the monopolistic innovator. By assuming that innovation follows a Poisson process, whose arrival rate depends on the amount of resources invested in R & D, we show that central authority provides higher level of social welfare than market instruments.
1. Introduction
During the last years, several authors have included R & D into the analysis of environmental policy incentives, giving life to a new research branch. This literature can be divided in two strands. The first one is characterized by the microeconomic approach, making use of the game theory in order to study the strategic behavior in equilibrium. The major parts of these models are characterized by a partial equilibrium approach, which can be static [1] or quasidynamic, where each actor-firm, regulator and innovator-chooses in a sequential way [2]. This literature captures several aspect, such as market conditions, uncertainty about the R & D success and the environmental damage. The second research strand follows the endogenous growth approach [3,4]. We concentrate the attention on the first case, where innovation is mainly firm specific and depends on the total amount of R & D needed to developing energy saving technologies.
In this kind of models, where innovation is a private good, the literature investigates upon the optimal policy instrument to develop and diffuse the new technology. There are two alternative strategies to do so: the ex ante and the ex post policy. Several authors assume that in the former there is only one innovator [5,6] or several identical firms, engaging in a patent race: in the latter just one innovator prevails in the market, gaining market power. This innovator can sell or license to the other firms which choose for adoption or not. For this reason it becomes crucial the commitment and the timing of policies, which can make the difference in terms of welfare results [7].
Denicolo was the first at explicitly comparing ex ante and ex post regulation both for emission taxes and tradable permits in a model with an upstream monopolistic R & D firm and many polluting downstream firms [4]. In this model the degree of emissions reduction depends on R & D investment and he finds that taxes and permits give the same results for ex post regulation. However, if the regulator adopts the ex ante policy, the first best equilibrium doesn’t exist, since both the instruments lead to underinvestment in R & D. The author shows an alternative solution, where the regulator can commit to the second-best optimal level of the instruments, but the choice depends on the social cost of pollution and there is no certainty about the effectiveness of taxes and permits.
Unlike most of other contributions, in Parry [8] there is free entry on both markets, and he shows that a higher tax rate produces a double effect: it involves a smaller number of polluting firms but we know that the firms with the highest willingness to pay for the new technology stay in the market, so a higher tax also induces a higher license fee. Parry [7] introduced some variations to his model and he investigated upon the magnitude of welfare gain coming from abatement cost reducing innovation, relative to the welfare gain induced by optimal pollution control over time. He found that this magnitude depends on three factors: the initially optimal abatement level, the speed at which innovation reduces future abatement costs (on the optimal innovation path) and the social discount rate. This factor plays a key role in the determinants controlling the welfare gain from innovation and pollution control. Parry shows that there are several scenarios where the welfare gains from innovation are smaller than those which come from the pollution control. In many cases the R & D investment decided by regulator does not coincide with the market decision. This result seems to contradict the earlier assertion by economist who supported the welfare gain from innovation.
Our paper is close in spirit to Denicolo [5] and Parry [6] and represents a further refinement of Gaeta [2], which analyzes how market instruments are able to mimic optimal social choice in driving the adoption of advanced oil saving technologies. In that paper the advanced technology was exogenously available to investing firms. This paper analyzes the case where the advanced technology comes from an innovating monopolistic firm investing in R & D. Main result is that, with endogenous R & D, the social planner provides Pareto optimal solution that market is not able to mimic. These results are in line with the cited literature, although our analysis involves a different microeconomic setup. Under this point of view our results confirm that market instruments provide sub-optimal oil usage amount in the economy. Even when we want to measure social welfare by means of the amount of R & D, as some authors point out, the central policy provides always higher level of investment than the free market.
2. The Model: Firms Behaviour and Market Instruments
We are going to assume an economy characterized by two sectors: manufacturing and R & D. In the manufacturing sector there are n firms acting in a competitive way. Production uses oil only. Oil is costly and polluting. Government wants to reduce oil usage in the economy by means of suitable policies. As in [1], there are two alternative oil saving technologies; conventional and advanced. The first one is promptly available free of charge; the second one involves a lump sum cost. Firms act by choosing optimal oil using; in a free market, without central policy, firms choose the maximum amount of oil,  With centralized policies, firms change their optimal plan; we are going to take into account how alternative oil saving policies (tax, permits and command and control) affect firms behaviour.
With centralized policies, firms change their optimal plan; we are going to take into account how alternative oil saving policies (tax, permits and command and control) affect firms behaviour.
2.1. Taxation
When firms are charged with a tax on the amount of oil usage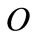 , profits are given by:
, profits are given by:
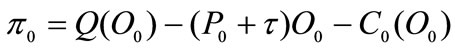 (1)
(1)
 (2)
(2)
where 0 means that the firm is not adopting the advanced technology and 1 the opposite. Functional assumptions are as usual:
 and
and  C is the oil saving cost related to the chosen technology. As usual we are going to assume convexity in C,
C is the oil saving cost related to the chosen technology. As usual we are going to assume convexity in C,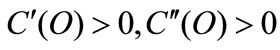
 .
. is the exogenous oil price and
is the exogenous oil price and 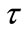 the tax rate. Moreover we assume that the advanced technology is more efficient in oil saving, thanks to research and development
the tax rate. Moreover we assume that the advanced technology is more efficient in oil saving, thanks to research and development  Efficiency is given by the r coefficient that depends on m, i.e.
Efficiency is given by the r coefficient that depends on m, i.e.  with
with 
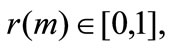 PR is the patent price paid by firms adopting the advanced technology.
PR is the patent price paid by firms adopting the advanced technology.
Firms maximize profits (equations (1) and (2)) with respect to the oil usage O0 and O1, given , PR and m. The optimal oil usage is implicitly given by the following first order conditions.
, PR and m. The optimal oil usage is implicitly given by the following first order conditions.

Whenever 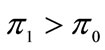 all firms are induced to adopt the advanced technology and so n1 = n Otherwise if
all firms are induced to adopt the advanced technology and so n1 = n Otherwise if  is not determined.
is not determined.
A single firm must choose which technology is going to adopt. This is done by comparing profits in both situations:
 (3)
(3)
R & D is performed by a single monopolistic firm. It invests m in R & D and obtains the new technology with probability p(m), that follows a Poisson process with cumulative distribution function  The R & D cost for unit of research is k so that the innovating firm produces a quantity of R & D that makes equal the expected profit to the actual cost of investing in R & D (this is standard in the neo-shumpeterian approach). The arbitrage equation is
The R & D cost for unit of research is k so that the innovating firm produces a quantity of R & D that makes equal the expected profit to the actual cost of investing in R & D (this is standard in the neo-shumpeterian approach). The arbitrage equation is
 (4)
(4)
We can solve this equation in order to get
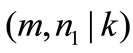 and then we substitute in the Equation (3). By doing so, we have
and then we substitute in the Equation (3). By doing so, we have 
In the decentralized economy 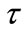 and n1 are exogenous to the firm, so firm behaviour in adopting or not the advanced technology depends on
and n1 are exogenous to the firm, so firm behaviour in adopting or not the advanced technology depends on  where m depends on the R & D firm.
where m depends on the R & D firm.
With partial adoption  and this leads to
and this leads to  The main goal is to investigate upon this relationship and on the general equilibrium of the economy.
The main goal is to investigate upon this relationship and on the general equilibrium of the economy.
With full adoption  and
and  In such a case the R & D firm chooses
In such a case the R & D firm chooses  in order to induce
in order to induce  but, once more, nothing assures that such equilibrium does exist and more analytical work must be developed.
but, once more, nothing assures that such equilibrium does exist and more analytical work must be developed.
2.2. Partial Adoption
Let us assume that the cost reduction function follows:
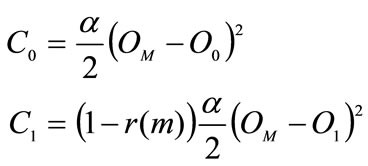
Profit maximization leads to:


where 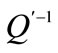 is the inverse first order derivative. When partial adoption is at work we have
is the inverse first order derivative. When partial adoption is at work we have 
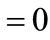 . Equilibrium is determined by closing the model through the R & D equation
. Equilibrium is determined by closing the model through the R & D equation  Nonetheless the left hand side is characterized by a strong non-linearity and in general not much can be said on the amount of R & D
Nonetheless the left hand side is characterized by a strong non-linearity and in general not much can be said on the amount of R & D  characterizing the equilibrium. For further investigation, we are going to assume homothetic production function,
characterizing the equilibrium. For further investigation, we are going to assume homothetic production function,  and that probabilities of new discovery follows a Poisson law
and that probabilities of new discovery follows a Poisson law  At the same time we are going to assume
At the same time we are going to assume 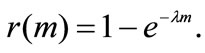
Let us investigate upon the first order conditions. Profit maximization leads to:
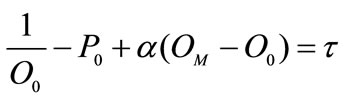 (5)
(5)
 (6)
(6)
First order conditions mean that firms uses oil until marginal profit is equal to the usage cost given by the tax rate. Solving Equations (5) and (6) provides optimal oil usage conditioned on the tax rate. Following lemma holds:
Lemma 1 First order conditions imply

Proof. When  we have
we have 
 Being
Being  Equation (6) lies everywhere under Equation (5). (end of proof).
Equation (6) lies everywhere under Equation (5). (end of proof).
Equation (6) links  to the amount of R & D via r(m). The relationship is linear-concave in r, being
to the amount of R & D via r(m). The relationship is linear-concave in r, being  a quadratic function. Following lemma holds:
a quadratic function. Following lemma holds:
Lemma 2  is decreasing in m.
is decreasing in m.
Proof. By normalizing  from Equation (6) we have:
from Equation (6) we have:
 with
with

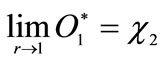 with
with

Given the linear concavity of  w.r.t.
w.r.t.  and being
and being  the lemma holds. (end of proof).
the lemma holds. (end of proof).
The lemma underlines the oil saving feature of R & D; more investment in new technologies has a positive effect in the economy as reduces the optimal amount of oil usage per firm.
Once the optimal oil usage  is carried out, Equation (2) provides the patent price
is carried out, Equation (2) provides the patent price 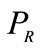 given the perfect market condition
given the perfect market condition 
 (7)
(7)
The Equation (7) sets the patent price that firms are allowed to pay for using the new technology. It depends on the optimal amount of R & D that the monopolistic firm is investing. The relationship is strongly non linear in  The equation can be rearranged in the following way:
The equation can be rearranged in the following way:
 (8)
(8)
with 
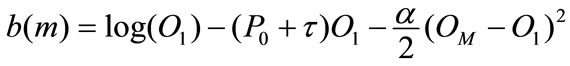
and

Following lemma holds:
Lemma 3  is increasing in m. Nevertheless second order derivative can not be signed unambiguously.
is increasing in m. Nevertheless second order derivative can not be signed unambiguously.
Proof. By deriving Equation (8) with respect to m we obtain:

We are going to assume that the term in brackets is negative and so, by Lemma 2,  Moreover:
Moreover:
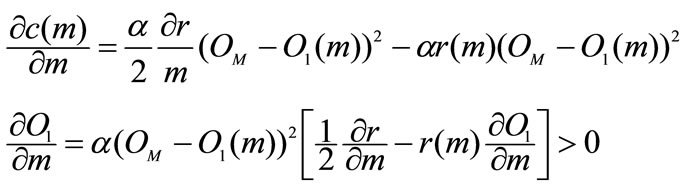
However, second order derivatives are not unambiguously determined and so convexity and concavity of the function can alternatively be viable. (end of proof).
The model is closed by analyzing how the monopolistic firm chooses the price  according to Equation (4).
according to Equation (4).
Following lemma holds:
Lemma 4 The supply curve for  is monotonically increasing in m.
is monotonically increasing in m.
Proof. Let us rewrite Equation (4) in the following way:

In a decentralized economy,  does not depend on
does not depend on . Hence:
. Hence:

and so:
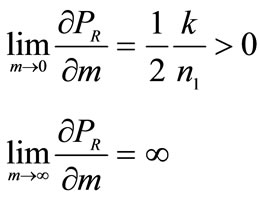
Moreover first derivative is zero only when  (end of proof).
(end of proof).
General equilibrium comes from comparing  by Lemmas 3 and 4, i.e. by crossing supply and demand for m. By Lemma 3, multiple equilibria are viable results. Nevertheless stable equilibrium requires that Brouwer's assumptions for fixed point are satisfied. In general, number and stability of equilibrium depend on parameters. Moreover, the general equilibrium depends on
by Lemmas 3 and 4, i.e. by crossing supply and demand for m. By Lemma 3, multiple equilibria are viable results. Nevertheless stable equilibrium requires that Brouwer's assumptions for fixed point are satisfied. In general, number and stability of equilibrium depend on parameters. Moreover, the general equilibrium depends on  and is not possible to asses how taxation affects market equilibrium. For such a reason the model will be numerically analyzed by normalizing
and is not possible to asses how taxation affects market equilibrium. For such a reason the model will be numerically analyzed by normalizing 
Following Figure 1 shows the equilibrium relationship in such a case.
Although we are working in a static context, some equilibria are unstable and so not robust at the bargaining process involved by  Stability of Brouwer fixed point theorem requires that first derivative be less than one in the neighborhood of the crossing point between demand and supply; this leaves just one single stable equilibrium. Since we are going to analyze the model by through some numerical investigations the unstable equilibria are ruled out from the analysis.
Stability of Brouwer fixed point theorem requires that first derivative be less than one in the neighborhood of the crossing point between demand and supply; this leaves just one single stable equilibrium. Since we are going to analyze the model by through some numerical investigations the unstable equilibria are ruled out from the analysis.
Table 1 sums up some numerical exercises (deep parameters .
.
Main findings are the strict non linearity of the functions;  is defined on a subset only of the feasible domain
is defined on a subset only of the feasible domain  according to the number of adopting firms. What is relevant is the monotonicity of m w.r.t.
according to the number of adopting firms. What is relevant is the monotonicity of m w.r.t. ; an increase in taxation, all other things equal, leads firms to reduce remarkably the oil usage in both technology. This induces the R & D firm to invest more and to charge a higher price (or conversely). This means that taxation matters for the amount of R & D in the economy. However it is hard to establish a hierarchy of equlibrium. With n1 = 0.25 the tax rate is high; this drives firms to reduce remarkably oil usage; nonetheless the maximum investment in R & D is obtained with n1 = 0.75. This warns us on the government objective function: as the literature remarks, by adopting the maximum investment in R & D or the lowest level of oil usage as the government objective function is not neutral for results. The first target involves lower level of taxation and conversely.
; an increase in taxation, all other things equal, leads firms to reduce remarkably the oil usage in both technology. This induces the R & D firm to invest more and to charge a higher price (or conversely). This means that taxation matters for the amount of R & D in the economy. However it is hard to establish a hierarchy of equlibrium. With n1 = 0.25 the tax rate is high; this drives firms to reduce remarkably oil usage; nonetheless the maximum investment in R & D is obtained with n1 = 0.75. This warns us on the government objective function: as the literature remarks, by adopting the maximum investment in R & D or the lowest level of oil usage as the government objective function is not neutral for results. The first target involves lower level of taxation and conversely.
2.3. Full Adoption
When  every firm invests in the advanced technology and n1 = 1. Profits are:
every firm invests in the advanced technology and n1 = 1. Profits are:

maximization leads to  In such a case the solution is quite simple; once solved for
In such a case the solution is quite simple; once solved for  the optimal amount of R & D can be carried out by Equation (4).
the optimal amount of R & D can be carried out by Equation (4).
3. Permits
Before analyzing the social planner problem, it is useful to compare results obtained in the tax case with alternative market based instruments. Let us start from permits. In such a case firms are permitted to use oil in a given amount. According to literature, we are going to distinguish between costly, auctioned and free permits (grandfathering). When firms are charged with a price  per unit of oil usage, results are not different from taxation. In fact, each firm acts in a price-taker environment, taking
per unit of oil usage, results are not different from taxation. In fact, each firm acts in a price-taker environment, taking  as the tax rate, i.e.
as the tax rate, i.e.  and Equations (1) and (2) are unchanged.
and Equations (1) and (2) are unchanged.
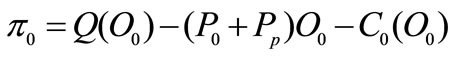 (9)
(9)
 (10)
(10)
With auctioned permits results are different. Let us assume that  permits are exogenously issued by central authority and
permits are exogenously issued by central authority and  be the market clearing price. Unlike costly permits, when partial adoption is at work, the following constraint must be satisfied:
be the market clearing price. Unlike costly permits, when partial adoption is at work, the following constraint must be satisfied:

where oil usage comes from firm first order conditions. This means that n1 is not a free parameter but depends on L:

By replying simulations by taking into account such a constraint leads to table 2.
By comparing results with the ones obtained with the tax rate, we can conclude that auctioned permits confirm the monotonicity of  w.r.t. the cost of oil usage related to permits; an increase in
w.r.t. the cost of oil usage related to permits; an increase in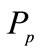 , all other things equal, leads firms to reduce remarkably the oil usage in both technologies and to increase the investment in R & D,
, all other things equal, leads firms to reduce remarkably the oil usage in both technologies and to increase the investment in R & D,  Nevertheless, auctioned permits allow less oil saving than non-auctioned permits (or taxation) and involve consequently a lower level of investment in R & D. As literature shows, taxation provides more incentive to firm
Nevertheless, auctioned permits allow less oil saving than non-auctioned permits (or taxation) and involve consequently a lower level of investment in R & D. As literature shows, taxation provides more incentive to firm
Table 2. Permits outcome.
in reducing oil usage.
The last case we are going to analyze is free permits (grandfathering); in such a case each firm is endowed with the permits of using a given oil quantity  However, since advanced technology allows firms to save out of oil, investor firms can trade their permits to notadopting ones. Partial adoption means that firms are indifferent and the following constraint must hold:
However, since advanced technology allows firms to save out of oil, investor firms can trade their permits to notadopting ones. Partial adoption means that firms are indifferent and the following constraint must hold:

given that  cancels out in both sides we obtain Equations (9) and (10). So incentive to adopt the new technology is the same under free or costly permits.
cancels out in both sides we obtain Equations (9) and (10). So incentive to adopt the new technology is the same under free or costly permits.
We can sum up results in the following proposition:
Proposition 5 Non auctioned and free permits allows same results in terms of oil saving and investment in R & D than auctioned permits.
4. Command and Control
This last section is devoted to the so called “command and control” policy; in such a case a firm is not allowed to use more than  units of oil. Firms are indifferent when the following condition is satisfied:
units of oil. Firms are indifferent when the following condition is satisfied:
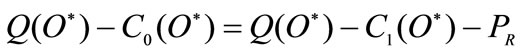
since 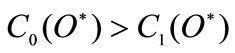 the above equation is decreasing in
the above equation is decreasing in  in other words, the relaxing of the constraint on oil usage reduces the incentive to adopt the new technology. This means that for
in other words, the relaxing of the constraint on oil usage reduces the incentive to adopt the new technology. This means that for  no firms will adopt the new technology and vice versa.
no firms will adopt the new technology and vice versa.
5. The Centralized Economy
In this section we are going to compare market equilibrium with the one chosen by a central authority. The central planner has to maximize the social welfare given by the private firm profit net of environmental damage, 
 (11)
(11)
The government chooses the optimal oil usage, the optimal number of adopting firms and leaves the optimal size of R & D to the monopolistic firm. The lagrangian function does not allow a closed form solution. We have to solve for:
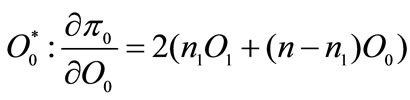 (12)
(12)
 (13)
(13)
Equations (12) and (13) mean that the private marginal profit must be equal to the marginal social cost; in the decentralized economy these must be equal to the tax rate.
The model is closed by:
 (14)
(14)
with:

The R & D is still determined by Equation (4) once that oil usage and market size are optimally chosen.
Basically the model uses a fixed point argument to find social optimum; Equations (12) and (13) provide 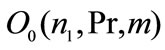 and
and . These results plugged in 14 provide solution for
. These results plugged in 14 provide solution for  and finally Equation (4) provides the optimal R & D.
and finally Equation (4) provides the optimal R & D.
Unfortunately the algebra can not be managed in an easy way. However, assumptions on functional form assure that an equilibrium do exist. Figure 2 shows Equation (14); as can be seen, it does exist  that satisfies the
that satisfies the  constraint.
constraint.
For analyzing the model, a numerical routine in Maple V has been written down. The routine follows a fixed point algorithm with a backward induction; by starting from a prior on m and  the optimal values for
the optimal values for ,
,  and
and  are calculated through Equations (12), (13) and (14). Then the prior is updated with Equation (4) and the routine goes on, until the fixed point is achieved.
are calculated through Equations (12), (13) and (14). Then the prior is updated with Equation (4) and the routine goes on, until the fixed point is achieved.
By using  the numerical simulation brings to this optimal value for oil usage and the consequent size of R & D.
the numerical simulation brings to this optimal value for oil usage and the consequent size of R & D.
The optimal number of adopting firms is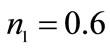 ; what is striking is the very low level of oil usage chosen by the central authority. The relative high demand for advanced technology pushes up the price of patents, which in turn induces the R & D firm to invest more. By comparing this solution to the ones obtained in the market analysis with
; what is striking is the very low level of oil usage chosen by the central authority. The relative high demand for advanced technology pushes up the price of patents, which in turn induces the R & D firm to invest more. By comparing this solution to the ones obtained in the market analysis with  the social planner chooses always the lowest level of oil. This is summarized in the following proposition.
the social planner chooses always the lowest level of oil. This is summarized in the following proposition.
Proposition 6 In the centralized economy, 60% of manufacturing firms uses the advanced technology for oil saving. This induces a very low level of oil usage per firm. By comparing such a result with market based instruments, the central economy provides the lowest level of oil usage with respect to the market equilibrium.
The difference between social and market equilibrium comes from the more complex relationship entailed by the social question. By comparing first order conditions in both situations, we have that, in the decentralized economy, the marginal profit is equal to the market instrument (tax or permits) which is exogenously given by the government. In the decentralized economy, first order conditions lead to:
 (15)
(15)
while in the centralized economy we have:

In the last equation both sides depend on the amount of R & D which responds to the amount of oil usage in the economy. Such a situation is completely different from the decentralized solution where tax can be exogenously adjusted in order to satisfy Equation (15).
This result is new in the literature; Parry 2003 achieves the opposite result in the context of pollution control. He finds that market based instrument provides higher pollution abatement than the social planner and in general the positive effect on the amount of R & D is small. In our case there is a strong effect on the optimal amount of investment in new technology. Had we assumed technological spillover, we would have added a positive effect to the development of economy, as in [9].
Similar result are instead shown in Denicolo, where tax and permits are not able to reach the first best optimal solution in an economy very close to the one we assumed. In his paper, the author makes a rank market instruments according to the incentive to innovate. Following Denicolo, we compute the welfare function W by using the different oil usage quantity arisen from different policies. Tables 4-6 sum up the previous findings adding the calculated welfare function  in the three policies: taxation, auctioned permits and social planner.
in the three policies: taxation, auctioned permits and social planner.
As results show, the highest value for  is obtained with the centralized solution. The picture is more fuzzy when we compare taxation and auctioned permits; it is not possible to find a strict hierarchy;
is obtained with the centralized solution. The picture is more fuzzy when we compare taxation and auctioned permits; it is not possible to find a strict hierarchy;  depends both on
depends both on  and tax rate or permits price.
and tax rate or permits price.
Finally, a last word on the number of adopting firm. Being the optimal number of adopting firm less than one (0.61 in our simulation) one can wonder how central authority can effectively implement this number in the economy. The same question arose in Gaeta [1], and it can be managed in same way, i.e. adopting a “multistage game with observed actions in a perfect information context” [10]. Nevertheless, this case can easily be managed by a command a control policy, where central authority commits both on the number of adopting firms (e.g. throughout permissions) and on the amount of oil usage. Results confirm that such a policy is successfully when R & D is endogenous.
6. Conclusions and Further Refinements
This paper analyzes the strong interplay between investment in R & D and firm behaviour in reducing oil usage. We show that market instruments are not able to mimic central authority. This is basically induced by the endogeneity of the R & D process. The result is similar to Denicolo, although under different assumptions. However, unlike this author, it is not possible to rank instruments on a Pareto ladder. There is a strong non-linearity in the behavioral equation and this reduces the relevant domain of existence. In general it is not possible to establish which instrument performs better. However it is true that higher taxation induces more investment in R & D, as in Parry and Denicolo.
This paper must be considered a first approach to the problem; however several refinements are possible. First of all, numerical simulations should call for some calibration to “stylized fact”. Unfortunately is very hard to find microdata on such phenomena; despite our efforts to get in touch with international agency we were not able to fill the gap. Second, we should analyze the case where central authority chooses the optimal amount of R & D, instead of leaving such decision to an external firm. This would be very close to Parry 1998.
[1] T. Requate, “Dynamic Incentives by Environmental Policy Instruments—A Survey,” Ecological Economics, Vol. 54, No. 2, 2005, pp. 175-195.
[2] E. G. Gaeta, “Environmental Policy and Firm Investment Behavior When Energy Saving Technologies are Available,” Mimeo, 2008.
[3] G. Barlevy, “On the Cyclicality of Research and Development,” Working paper, Federal Reserve Bank of Chicago, 2006.
[4] Y. Tsur and A. Zemel, “Scarcity, Growth and R & D,” Journal of Environmental Economics and Management, Vol. 49, No. 3, 2005, pp. 484-499.
[5] V. Denicolo, “Pollution-Reducing Innovations under Taxes or Permits,” Oxford Economic Papers, Vol. 51, No. 1, 1999, pp. 184-199.
[6] C. Fisher, I. Parry and W. Pizer, “Instrument Choice for Environmental Protection When Technological Innovation is Endogenous,” Journal of Environmental Economics and Management, Vol. 45, No. 3, 2003, pp. 523-545.
[7] I. W. H. Parry, W. A. Pizer and C. Fischer, “How Large are the Welfare Gains from Technological Innovation Induced by Environmental Policies?” Journal of Regulatory Economics, Vol. 23, No. 3, 2003, pp. 237-255.
[8] I. Parry, “Optimal Pollution Taxes and Endogenous Technological Progress,” Resource and Energy Economics, Vol. 17, No. 1, 1995, pp. 69-85.
[9] I. Parry, “Pollution Regulation and the Efficiency Gains from Technological Innovation,” Journal of Regulatory Economics, Vol. 14, No. 3, 1998, pp. 229-254.
[10] D. Fudenberg and J. Tirole, “Game Theory,” MIT Press, 7th Edition, 2000.