Optimal Operation of Multi-Objective Hydropower Reservoir with Ecology Consideration ()
1. Introduction
As a kind of clean and renewable energy, hydropower resources, once being used fully and reasonably, can not only reduce the consumption of primary energy but also lessen the environmental stress caused by thermal power and other energy sources, thus it can cut down greenhouse gases emissions. Therefore, every country attaches great importance to hydropower development. Since 2008, the hydropower installed capacity in China has reached 172 million kW, ranking first worldwide, and annual electricity generation has reached 563.3 billion kW·h, accounting for 16.4% of the total national annual energy output. At present, hydropower occupies an important position in Chinese energy construction and existing energy structure. The construction and operation of reservoirs have played an important role on flood control, electricity generation, urban and rural water supply and irrigation, however, it has also brought negative effects to the fragile river ecosystem due to reservoir construction itself and its operation mode. The former can be solved by ecological restoration, and the latter may be eased through consideration of ecological reservoir operation mode. At the moment, scholars home and abroad have conducted researches towards the ecological issues of reservoir scheduling and achieved considerable results. Cavallo [1], Lence etc. [2] studied the ecological scheduling model of reservoir and applied the model in practical operation. Domestic Changjiang Water Resources Committee has studied the ecological scheduling of the Three Gorges Reservoir to guarantee the ecological and environmental water demands in Yangtze River region [3,4]. Yellow River Conservancy Commission conducted prototype tests of “water and sediment regulation” towards the jointscheduling of China Xiaolangdi Reservoir, etc. Dong etc. [5] pointed out that at the same time of realizing multiple objectives of social economy, river ecological requirement should also be taken into consideration and multiobjective ecological scheduling of reservoir should be enforced. Liu [6], Yang, etc. [7] raised the quantitative calculation method of ecological water demand to prevent river sediment deposition and they asserted that the average annual water that can maintain river balance and can prevent the river sediment in the downstream of the Yellow River is 18.4 billion ton. Hu, etc. [8] proposed the reservoir ecological scheduling method based on ecological flow process line. Yu, etc. [9] discussed the notion and method concerning reservoir ecological water level and ecological capacity of preparatory reservoir. Consequently, ecological factor has become a significant issue that deserves great concern in reservoirs scheduling. Based on previous research achievements, and by coupling reservoirs ecological and generation scheduling, this paper discusses optimal operation of hydropower reservoir with ecology consideration and employs Chaotic Genetic Algorithm (CGA) to seek the solution.
2. Mathematical Model for Optimization of Ecology-Oriented Multi-Objective Hydropower Reservoir
Conventional reservoirs scheduling norm mainly aims at flood control and benefit promotion rather than ecology factor. To enforce ecological reservoirs scheduling needs newly-established standard and clear awareness of the priorities of flood control, benefit promotion and ecology. In general, reservoirs scheduling should adhere to the operation principle that giving absolute priority to flood control while harmonize, unify and overall consider economical and ecological scheduling.
2.1. Objectives
Objectives of ecology-oriented multi-objective reservoirs optimization include the maximum annual power generation benefit, the maximum output of the minimal output stage in the year and the minimum shortage of eco-environment water demand in reservoir region and downstream river.
1) Maximum annual power generation benefit Taking maximum annual power generation benefit as optimization criterion, and under the steady operation of electrical power system, adopting the maximum annual power generation benefit in the year as the objective function of reservoirs optimal operation model.
 (1)
(1)
where, E is the annual generation of hydropower stations, kW·h. A is the power generation coefficient. Qt is the turbine release water discharge for power generation at time period t, m3/s. Ht is the average head at time period t, m. T is the total period count within a year, T = 12. Mt is the amount of hours at time period t.
Taking maximum annual power generation benefit as optimization criterion means to take consideration of the on-grid price difference in high, normal and low flow periods and to increase the generation benefits during high and normal flow period as much as possible while enhancing the generating income during low flow period via reservoir regulation.
 (2)
(2)
where, F is annual generation benefits (RMB). Pt is the electricity price factor during time period t.
2) Maximum output of the minimal output stage in the year.
Maximum output of the minimal output stage in the year is required to achieve. The effect of this objective is to provide possibly maximized, uniform and reliable output for the power grid, to give full play to hydropower capacity benefits and to replace the thermal power capacity.
 (3)
(3)
where, NP is the maximum output of the minimal output stage in the year (MW).
3) Minimum shortage of eco-environment water demand in reservoir region and downstream river.
 (4)
(4)
where, Z is the shortage of eco-environment water demand.  is the shortage of eco-environment water demand of downstream watercourse during time period t.
is the shortage of eco-environment water demand of downstream watercourse during time period t. 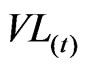 is the shortage of eco-environment water demand in reservoir region. N is the total amount of time periods.
is the shortage of eco-environment water demand in reservoir region. N is the total amount of time periods.
For the calculation of eco-environment water demand please refer to literature [10]. Concerning that there are still disputes over the researches of eco-environment water demand, some scholars have raised the notion of minimum and appropriate eco-environment water demands. In the paper, calculation of eco-environment water demand is based on the minimum eco-environment water demand. Hence, Equation (4) can be turned into
 (5)
(5)
where, ,
, are the minimum eco-environment water demand of the downstream river and the reservoir itself during time period t respectively.
are the minimum eco-environment water demand of the downstream river and the reservoir itself during time period t respectively. ,
, are the water supplies of downstream river and reservoir itself during t period respectively.
are the water supplies of downstream river and reservoir itself during t period respectively.
Conventional reservoir scheduling mainly considers social and economic objectives and rarely pay attention to the eco-environmental demands, thus causing the ecological deterioration in reservoir itself and the downstream watercourse. Taking the minimum shortage of ecoenvironment water demand in reservoir region and downstream river as optimization criterion fully reflects awareness of eco-environmental protection of reservoir regions and its downstream watercourses. In this way, basic water usage of human life and eco-environmental demand are being regarded equally important, which is significant to river protection as well as the promotion of sustainable utilization of water resources.
2.2. Constraints
Constrains of hydropower stations Optimization are mainly as follows:
1) Water balance equation
 (6)
(6)
where,  is the reservoir storage volume at the end of time period t, m3. Vt is the reservoir storage volume at the beginning of time period t, m3. qt is the average reservoir inflow at time period t, m3/s. Qt is the turbine release water discharge for power generation at time period t, m3/s. Kt is the conversion coefficient of time length.
is the reservoir storage volume at the end of time period t, m3. Vt is the reservoir storage volume at the beginning of time period t, m3. qt is the average reservoir inflow at time period t, m3/s. Qt is the turbine release water discharge for power generation at time period t, m3/s. Kt is the conversion coefficient of time length.
2) Reservoir storage capacity limits At any time, the volume of reservoir storages should be between the minimum and the maximum.
 (7)
(7)
where,  is the minimum consent water volume of reservoir at time period t, m3.
is the minimum consent water volume of reservoir at time period t, m3.  is the maximum consent water capacity of reservoir at time period t, m3.
is the maximum consent water capacity of reservoir at time period t, m3.
3) Reservoir discharge limits
 (8)
(8)
where,  is the minimum water discharge of reservoir at time period t, m3/s.
is the minimum water discharge of reservoir at time period t, m3/s.  is the maximum water discharge of reservoir at time period t, m3/s.
is the maximum water discharge of reservoir at time period t, m3/s.
4) Hydropower station power generation limits.
 (9)
(9)
where,  is the hydro plant minimum power generation constraint of reservoir at time period t, kW.
is the hydro plant minimum power generation constraint of reservoir at time period t, kW.  is the maximum consent water volume of reservoir at the beginning of period t, m3.
is the maximum consent water volume of reservoir at the beginning of period t, m3.
5) Boundary constraints
 (10)
(10)
where,  is the initial reservoir storage volume for K time of iteration.
is the initial reservoir storage volume for K time of iteration.  is the final reservoir storage volume after K time of iteration.
is the final reservoir storage volume after K time of iteration.
6) Variable non-negative constraint
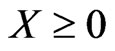 (11)
(11)
where, X is the variable that formed by decision variable.
3. Optimal Operation Model Based on Chaotic Genetic Algorithm
Optimization of hydropower stations is a rather complicated and nonlinear issue. Scholars from home and abroad have studied the issue with various methods, among which there are the relatively commonly-used dynamic programming (DP) [11], particle swarm optimization (PSO) [12], genetic algorithm (GA), [13,14] and chaotic optimization algorithm (COA) [15]. However, these methods also have obvious defects: DP method occupies too much computer memory, computes slowly and has the problem of curse of dimensionality. POA method is easily trapped into local optimum and thus reduces computation speed greatly. Large System Hierarchical method needs to add coordination factor and thus the computation becomes more complex and convergence speed is low. PSO method relies on little empirical parameters and has a high convergence speed, but there are also deficiencies of low accuracy and easily being trapped into local optimum. GA method has the deficiencies of precocity and low searching efficiency. Wang [16] conducted a research towards reservoir scheduling model based on the coupling of chaotic and genetic algorithms and this coupled algorithm shows better performance compared with the conventional GA, unfortunately the genetic algorithm that the author employed is basic algorithm, thus is not unsatisfactory. Based on previous research achievements, an optimal operation algorithm of hydropower reservoir based on CGA is put forward.
3.1. Basic Idea of Chaotic Genetic Algorithm
CGA couples Chaotic Optimization Algorithm with Genetic Algorithm and benefits from the complementary advantages. First, take advantage of ergodicity of COA and amplify the chaotic sequences produced by Logistic mapping to the range of the optimized variable. Then, carry out operations of selection, crossover and mutation by optimized search mechanism of the GA. Meanwhile, add chaotic disturbance operator to get the new population, then via generations of iterative optimization to get the optimum solution satisfying the convergence condition, then add another chaotic disturbance to the initial optimum solution and launch local elaborate search to seek the optimum solution of the original problem. The chaotic disturbance operators in the CGA are added for two reasons. First, to get the new population to avoid precocity by relying on the chaotic disturbance of the chromosome in the genetic operation process. Second, to launch local elaborate search with the help of chaotic disturbance of the initial optimum solution after the convergence of the GA operation.
Chaotic disturbance of the chromosome in the genetic operation process: Suppose g as times of the current iteration,  (M is population scale. n is the amount of decision variable) as the new population after operations of selection, crossover and mutation after g times of iteration. Suppose
(M is population scale. n is the amount of decision variable) as the new population after operations of selection, crossover and mutation after g times of iteration. Suppose  (
( ) as the sequence produced by the Number j Logistic mapping,
) as the sequence produced by the Number j Logistic mapping,  as the array composed with n chaotic sequences. Sum the original population
as the array composed with n chaotic sequences. Sum the original population  with the array obtained via chaotic mapping correspondingly to get the new population
with the array obtained via chaotic mapping correspondingly to get the new population .
.
Chaotic disturbance of initial optimum: map the initial optimum ( ) that satisfy the iteration time to chaotic variable interval (0, 1) respectively to get the initial decision variable, as
) that satisfy the iteration time to chaotic variable interval (0, 1) respectively to get the initial decision variable, as , get chaotic sequence after K times iteration of chaotic mapping function (K is the length of chaotic sequence), then
, get chaotic sequence after K times iteration of chaotic mapping function (K is the length of chaotic sequence), then  is the k th variable of the chaotic sequence (
is the k th variable of the chaotic sequence ( ), suppose
), suppose  is the variables that consists of n
is the variables that consists of n , then
, then  can be obtained by Equation (12).
can be obtained by Equation (12).
 (12)
(12)
where,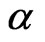 is a constant between (0, 1) and can be chosen adaptively,
is a constant between (0, 1) and can be chosen adaptively, is larger in initial searching phase and smalller in later phase.
is larger in initial searching phase and smalller in later phase. can be defined by Equation (13).
can be defined by Equation (13).
 (13)
(13)
where, m is positive integer and is defined based on the number of functions, usually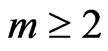 . k is iterative times.
. k is iterative times.
3.2. Steps for Hydropower Station Optimization Model Based on CGA
CGA is used to solve the hydropower station scheduling, and the steps are as follows:
Step 1: Divide the time period for the optimization of hydropower station, and determine the decision variables and its range. This mathematical model is divided into T time period, and takes the water levels of reservoir as decision variables, with the range between .
.
Step 2: Parameter setting. Set the number of variables, population size of genetic algorithm is M, the Termination iteration of GA is T, probability of crossover is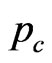 , mutation rate is
, mutation rate is .
.
Step 3: Objective function processing. Change the former Multi-objective problem to Single objective optimization problems by multi-objective decision-making technique.
Step 4: Constraint processing. For decision variables that correspond to unsatisfactory chromosome, its fitness value take one small numerical close to zero until all chromosomes that searched out can meet the constraints.
Step 5: Population Initialization. First choose the n different initial, then chaotic sequence is produced by Logistic Mapping Equation,
is produced by Logistic Mapping Equation,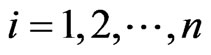 ,
, , p is the length of chaotic sequence. The Logistic Mapping Equation is (14):
, p is the length of chaotic sequence. The Logistic Mapping Equation is (14):
 (14)
(14)
where, is the control parameter.
is the control parameter.
Then by mapping various variables above according to Equation (15), we can get the initial population.
 (15)
(15)
where,  and
and 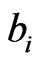 are the lower limit and the upper limit of decision variable
are the lower limit and the upper limit of decision variable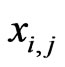 .
.
Step 6: Coding. Code the decision variable by the floating-point yards.
Step7: Operations of Selection, crossover and mutation. The probability of selection is selected by Stochastic Tournament Model, the crossover operator is the arithmetical crossover, and mutation operator is Uniform mutation operator.
Step 8: Calculate the function. Select proper fitness function, calculate fitness value.
Step 9: Retention strategies. sequencing fitness value from big to small, take the superior 10% to the next generation directly, then conduct selection, crossover and mutation operations again, calculate the new fitness value and sequence fitness value from big to small, replace the 10% bad chromosome in fitness value in population with the reserved 10% chromosome in former generation, conduct chaotic mutation towards other chromosome to get a new population.
Step 10: Output the initial optimal solution. Rearrange the population; calculate the difference value between Maximum fitness value and the average fitness value. If the difference value is among the permissible error that set, or the iteration reach maximum time that set, then output initial optimal solution, otherwise turn to Step 9.
Step 11: The chaotic mutation of initial optimal solution. Conducting chaotic mutation towards the optimal decision vector corresponding to the initial optimal solution, chaotic sequence is also produced by Logistic mapping equation, the length of sequence is K, get the chaotic decision-making vector after K group chaotic mutation.
Step 12: Output the optimal solution. Map the chaotic mutation variables above to the feasible region, calculate and compare the fitness values, the maximum is the optimum, the corresponding decision variable is the optimum decision variable, output the optimum.
4. Case Study
Take Wanjiazhai Hydropower Station on the Yellow River as an example. The stage-discharge curve of downstream channel and stage-storage capacity curve are known. The total capacity of the reservoir is 896 million. The utilizable storage is 445 million. The dead water level is 948 m. The normal water level is 977.0 m. The flood limit level is 966.0 m. The comprehensive efficiency coefficient is determined as 8.3. The guaranteed output is 185 MW. The installed capacity of the hydropower station is 1080 MW. The maximum discharge capacity is 1000 m3/s. Based on the incoming runoff data in normal flow year, the optimized scheduling calculation with the aforementioned model and algorithm is carried out.
The model takes the maximum annual power generation benefit, the maximum output of the minimal output stage in the year and the minimum shortage of eco-environment water demand as objectives. In the process of practical solution, turn the maximum output and the minimum shortage of eco-environment water demand into constraint conditions through constraint method. The concrete operation ideas are as follows. First, amplify the guaranteed output as the low limit of output in minimal output stage, which needs to be determined via repeating program operation. This paper finally regards 189 MW as minimum output for every time period. Second, turn the minimum shortage of eco-environment water demand to two constraints, i.e. the minimum shortage of eco-environment water demand in downstream watercourse, and the minimum shortage of eco-environment water demand of reservoir itself. At last, aiming at the maximum electricity generation, and take a water year as a cycle, divide the scheduling period into 12 sessions with every month as a period. The comprehensive efficiency coefficient is determined as 8.3. The head loss is 0.5 m. In the model, the initial value of Logistic mapping randomly lies between 0.51 and 0.74 with the controlling value decided as  = 4, the length of the chaotic sequence decided as 1000, the initial population of the model decided as 1000, the crossover rate decided as 0.9, the mutation rate decided as 0.1, the allowable error decided as 1.0 × 10–8, the maximum iterations decided as 200 (Table 1).
= 4, the length of the chaotic sequence decided as 1000, the initial population of the model decided as 1000, the crossover rate decided as 0.9, the mutation rate decided as 0.1, the allowable error decided as 1.0 × 10–8, the maximum iterations decided as 200 (Table 1).
As for the constraint for minimum eco-environment water demand in downstream watercourse, calculate the minimum eco-environment water demand in downstream watercourse through Tennant and minimum monthly runoff method and choose the larger value. Take the reservoir let-down flow as the eco-environmental water supply in watercourse, which minus the minimum of ecoenvironment water demand in downstream watercourse we can get the minimum shortage of eco-environment water demand in downstream watercourse. Obviously, a 0 minimized minimum shortage of eco-environment water demand in downstream watercourse is good for river health. Ecological river flow process in normal flow year is shown in Table 2. As for the minimum eco-environment water demand in reservoir, and considering the inactive storage capacity of Wanjiazhai reservoir being

Table 1. Ecology-oriented reservoir optimization results.

Table 2. Operation results for different algorithm.
451 million m3, then take the inactive storage capacity as the eco-environmental water supply in the reservoir region, then the minimum eco-environment water demand in reservoir is less than the inactive storage capacity. Therefore, the minimum eco-environment water demand in reservoir itself is satisfied. The ecological impoundment level is 948 m.
From Table 1 we can see that the water levels at the beginning and end of each month meet the level bound and each month’s output is within the control range. Meanwhile, the hydropower generation flow rate satisfies the eco-environmental water demand in downstream watercourses. Consequently, the calculation results fulfill the requirement. After optimized scheduling, the average annual energy output is 2.906 billion kW·h.
Apply the same model and method to the incoming runoff conditions of high (P = 10%) and low (P = 90%) flow annum, then the average annual energy output is respectively 2.983 and 2.635 billion kW·h. Therefore, the average annual energy output calculated through the model and algorithm in this paper is 2.841 billion kW·h which has an 0.091 billion kW·h (3.32%) increase in contrast with the 2.75 billion kW·h under routine scheduling. Then compare DP, GA, COA and CGA with one another, the results are shown in Table 2. From Table 2 we can see that after coupling GA and COA, CGA method can get the maximum average annual energy output. Hence, CGA is a good algorithm for solving reservoir optimized scheduling model which has advantages of high search efficiency, fine convergence and being closer to the global optimum solution, etc. Of course, it has a longer computation time than DP and GA method because of the demand for larger number of populations to realize ergodic search.
This paper has also studied reservoirs scheduling without ecology consideration. Take the maximum annual power generation benefit and the maximum output of the minimal output stage in the year as objectives, ignore the ecological water demand for constraint conditions, emply the same method to explore the scheduling of Wanjiazhai Hydropower Station. The results of normal flow annum condition are shown in Table 3. Under normal flow annum condition, compare the scheduling results with ecology consideration and without (see Table 4).

Table 3. Corresponding scheduling results without ecology consideration.

Table 4. Comparison of scheduling results with/without ecology consideration.
If ecology is not considered, annual electricity generation of optimized scheduling is 2.921 billion kW·h which is 0.015 billion kW·h more than the ecology-considered situation. But from Table 4 we can see, the let-down flow rate in both January and February is less than the minimum eco-environmental water demand flow rate.
Similarly, apply the optimized scheduling method to the incoming runoff conditions of high (P = 10%) and low (P = 90%) flow annum without eco-environmental consideration, then the average annual energy output after scheduling in high and low flow annum is respectively 3.005 and 2.621 billion kW·h. Therefore, the average annual energy output calculated through the model and algorithm in this paper is 2.849 billion kW·h which has an increase of 0.099 billion kW·h (3.7%) in contrast with the 2.75 billion kW·h under routine scheduling. Under average annual conditions, the comparison of the scheduling results with and without ecology consideration is shown in Table 5.
From Table 5, the average annual energy output has an increase of only 0.008 billion kW·h (about 0.28%) compared with scheduling that with ecology consideration. However, if ecology is not considered, there will be certain negative influence on the river ecology and environment. The reservoir optimized scheduling with ecology consideration will be beneficial to the protection of river ecology and environment and the promotion of sustainable use of water resources. Thus it’s worthy and necessary to gain the harmonious development of social economy and environment at the cost of little electricity generation benefit.
5. Conclusions
With the deepened awareness of eco-environment of people and the proposal of the concept of harmonious coexistence between man and water, the future trend of reservoirs scheduling is to couple ecological scheduling with generation scheduling, and to research on reservoir optimized scheduling mode that adapts to the social economy development and ecological protection. This paper takes full consideration of eco-environment factors in generation scheduling, and adds the objective of the

Table 5. Comparison of the scheduling results with and without ecology consideration (annual average).
minimum shortage of eco-environment demand in reservoir and the downstream watercourse. In practical calculation, turn this objective to two constraints through constraint method, i.e. satisfy the minimum eco-environment demand in reservoir and in the downstream watercourse. Case study indicates that the electricity generations of optimized scheduling with and without ecology consideration are nearly the similar, and that there will be certain negative influence on the river ecology and environment if ecology is not considered. In addition, this paper adopts the Chaotic Genetic Algorithm in disturbance model and CGA has advantages of high search efficiency, fine convergence and being closer to the global optimum solution, etc. All that mentioned above contributes to the enrichment and development of the theory and methods of reservoir optimized scheduling. Of course, the Chaotic Genetic Algorithm needs a longer computation time than GA method because of the demand for larger number of populations to realize ergodic search. In addition, there are still dispute over the computing methods of the eco-environmental water demand in reservoir regions and downstream watercourses, thus more scientific and reasonable eco-environment water demand pattern and computing method are essential. These are the aspects in need of further improvement.