Construction and Weight Distributions of Binary Linear Codes Based on Deep Holes ()
1. Introduction
Let  be the finite field with q elements, where q is an odd prime. An
be the finite field with q elements, where q is an odd prime. An  linear code
linear code  is a k-dimensional subspace of the vector space
is a k-dimensional subspace of the vector space 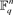 with minimum distance d, where
with minimum distance d, where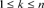 . The weight of code x is denoted by
. The weight of code x is denoted by . The dual code of
. The dual code of , denoted by
, denoted by , is defined by
, is defined by

Clearly,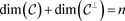 .
.
For the linear code  with length n, the number of codewords of weight i denotes
with length n, the number of codewords of weight i denotes 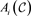 with
with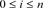 . The weight enumerator of
. The weight enumerator of  is defined by
is defined by
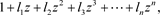
and the sequence  is said to be the weight distribution of
is said to be the weight distribution of . If the number of non-zeros in the sequence is t, then we say that the linear code is a t-weight code. The weight distributions of linear codes not only give the important information of linear codes in practice and theory, but also reflect the error-correcting ability of linear codes and the probability of error information occurring during transmission. In general, it is not effortless to determine the weight distributions of linear codes.
. If the number of non-zeros in the sequence is t, then we say that the linear code is a t-weight code. The weight distributions of linear codes not only give the important information of linear codes in practice and theory, but also reflect the error-correcting ability of linear codes and the probability of error information occurring during transmission. In general, it is not effortless to determine the weight distributions of linear codes.
The coset of , denoted by Q, is defined by
, denoted by Q, is defined by
![]()
where ![]() is a vector fixed for the given representation. The weight of Q is the smallest Hamming weight of the codewords of Q.
is a vector fixed for the given representation. The weight of Q is the smallest Hamming weight of the codewords of Q.
For any vector (codeword)![]() , the error distance to code
, the error distance to code ![]() of a received codeword u is defined by
of a received codeword u is defined by
![]()
where the minimum Hamming distance between vectors u and c is defined to be
![]()
The maximum error distance is defined by
![]()
where ![]() is called the covering radius of the linear code
is called the covering radius of the linear code![]() . If the error distance to code
. If the error distance to code ![]() of a received word
of a received word ![]() reaches the covering radius of linear code
reaches the covering radius of linear code![]() , the vector u is called the deep hole.
, the vector u is called the deep hole.
Deep holes have been widely studied in RS codes, and the deep holes of standard RS codes are given in [1] . In addition, Zhang et al. also gave deep holes for several classes of special codes in [2] [3] [4] . Therefore, most scholars are keen on studying the deep holes of some special codes. However, there is little work on constructing general linear codes from deep holes. Thus, we further consider the use of deep holes to construct some binary linear codes.
Around the 1960s, BCH codes were proposed by Hocquenghem [5] and Bose and Ray-Chaudhuri [6] , and the error-correcting codes were studied by Gorenstein and Zierler [7] over finite fields. In 1960, Gorenstein et al. [8] showed that the covering radius of binary 2-error-correcting BCH codes was 3, and further, the covering radius of the extended codes was 4. The study of 2-error-correcting BCH codes is very thorough, including covering radius, weight distribution, coset weight distribution and so on. The covering radius of the 2-error-correcting binary primitive BCH codes is known. From the definition of deep holes, we know that the deep holes of these BCH codes exist. Since linear codes play an important role in the fields of data storage, information security and secret sharing, the construction of linear codes is one of the important contents in the current cryptography and coding research. Therefore, it is very meaningful to construct binary linear codes.
In this paper, our main work is to construct some binary linear codes by combining deep holes with BCH codes. Furthermore, we can determine the parameters and the weight distributions of the binary linear codes. Finally, some examples are presented by Magma experiments, which support the weight distributions of these binary linear codes. These experimental results coincide with the theoretical results.
The rest of this paper is outlined as follows. Section 2 states some notations and results about narrow-sense binary primitive BCH codes and linear codes. In Section 3, three classes of binary linear codes are constructed and their parameters are determined. In Section 4, the weight distributions of these binary linear codes are obtained. Finally, the conclusion of this paper is given.
2. Preliminaries
In this section, we state some basic facts and known results about linear codes and narrow-sense binary primitive BCH codes.
2.1. The Weight Distributions of the Linear Code and Its Dual Code
For an ![]() linear code
linear code ![]() over
over![]() , and denote its dual by
, and denote its dual by![]() . The weight distribution of
. The weight distribution of ![]() can be uniquely determined by the weight distribution of
can be uniquely determined by the weight distribution of ![]() and vice versa. This linear relationship is crucial for investigating and calculating weight distribution, and we call it the MacWilliams identity.
and vice versa. This linear relationship is crucial for investigating and calculating weight distribution, and we call it the MacWilliams identity.
Let ![]() and
and ![]() be the number of codewords of weight j in
be the number of codewords of weight j in ![]() and
and![]() , respectively. The MacWilliams identity is defined by
, respectively. The MacWilliams identity is defined by
![]() (1)
(1)
Equivalently, we have
![]() (2)
(2)
and it is more convenient for us to calculate. But it involves the Stirling numbers ![]() of the second kind, where
of the second kind, where ![]() is defined by
is defined by
![]() (3)
(3)
In particular, ![]() if
if ![]() and
and![]() .
.
In binary codes, from (2), we deduce
![]() (4)
(4)
From (2), the first four Pless power moments are listed as follows ( [9] , p. 259):
![]()
![]()
2.2. Cyclic Codes and Narrow-Sense BCH Codes
An ![]() linear code
linear code ![]() over the finite field
over the finite field![]() , it is said to be cyclic if the codeword
, it is said to be cyclic if the codeword ![]() implies
implies![]() . For each vector
. For each vector![]() , define
, define![]() , any code
, any code ![]() corresponds to a subset of quotient ring
corresponds to a subset of quotient ring![]() . Note that a linear code
. Note that a linear code ![]() is cyclic if and only if the corresponding subset is an ideal of the quotient ring
is cyclic if and only if the corresponding subset is an ideal of the quotient ring![]() . Besides, every ideal of
. Besides, every ideal of ![]() is principal. Thus, every code
is principal. Thus, every code ![]() can be expressed as
can be expressed as![]() , where
, where ![]() is monic and has the smallest degree.
is monic and has the smallest degree. ![]() is said the generator polynomial, and
is said the generator polynomial, and ![]() is referred to as the check polynomial of
is referred to as the check polynomial of![]() .
.
Let![]() , where m is an integer with
, where m is an integer with![]() . Let
. Let ![]() be a primitive element of
be a primitive element of![]() . In addition, let
. In addition, let ![]() be the minimal polynomial of
be the minimal polynomial of ![]() with
with ![]() over
over![]() . For any
. For any![]() , define
, define
![]()
where ![]() denotes the least common multiple of these minimal polynomials.
denotes the least common multiple of these minimal polynomials.
Let ![]() denote the cyclic code with generator polynomial
denote the cyclic code with generator polynomial![]() , then we know
, then we know![]() . The set
. The set ![]() is described as a narrow-sense primitive BCH code with design distance
is described as a narrow-sense primitive BCH code with design distance![]() . An
. An ![]() linear code
linear code ![]() is said e-error-correcting if
is said e-error-correcting if![]() .
.
Let E denote the 2-error-correcting binary primitive BCH codes, and denote its dual by![]() . The code E is an
. The code E is an ![]() linear code, for
linear code, for![]() . The code E has parity-check matrix
. The code E has parity-check matrix ![]() defined by
defined by
![]()
The code E consists of all binary codewords ![]() such that
such that![]() . The extended code of B denote
. The extended code of B denote ![]() and denote its duals by
and denote its duals by![]() . A vector r of
. A vector r of ![]() is
is ![]() where
where![]() . The code
. The code ![]() has parameters
has parameters ![]() for
for![]() . The parity-check matrix
. The parity-check matrix ![]() is defined by
is defined by
![]()
where ![]() is an element of order
is an element of order ![]() in
in![]() . The code
. The code ![]() consists of all binary codewords
consists of all binary codewords ![]() such that
such that![]() .
.
2.3. The Weight Distributions of 2-Error-Correcting Binary Primitive BCH Codes and the Extended Codes
In this subsection, we introduce the weight distributions of the 2-error-correcting binary narrow-sense BCH codes and of their extensions, whose length are respectively ![]() and
and![]() .
.
The code ![]() is an
is an ![]() linear code in [10] , for odd
linear code in [10] , for odd![]() . The code
. The code ![]() is a binary linear code with the weight distribution in Table 1.
is a binary linear code with the weight distribution in Table 1.
The code ![]() is an
is an ![]() linear code in ( [11] , Table 16.5), for odd
linear code in ( [11] , Table 16.5), for odd![]() . The code
. The code ![]() is a binary linear code with the weight distribution in Table 2.
is a binary linear code with the weight distribution in Table 2.
The code ![]() is an
is an ![]() linear code, for even
linear code, for even![]() . The code
. The code ![]() is a binary linear code with the weight distribution in Table 3.
is a binary linear code with the weight distribution in Table 3.
Lemma 1. ( [9] , Lemma 7.5.1) Let ![]() be an
be an ![]() linear code over
linear code over![]() . Suppose u is a vector in
. Suppose u is a vector in ![]() but not in
but not in![]() . The linear code is generated by
. The linear code is generated by ![]() and u, which is an
and u, which is an ![]() linear code. Let D be this linear code, then we have
linear code. Let D be this linear code, then we have
![]()
![]()
Table 1. The weight distribution of![]() , for odd
, for odd![]() .
.
![]()
Table 2. The weight distribution of![]() , for odd
, for odd![]() .
.
![]()
Table 3. The weight distribution of![]() , for even
, for even![]() .
.
In binary codes, it is clear that we have
![]()
In other words, we have
![]()
Theorem 2. ( [9] , Th. 7.3.1) Let T be a set ![]() with
with![]() . The weight distribution of
. The weight distribution of ![]() and
and ![]() are determined by
are determined by ![]() and the
and the ![]() with
with![]() .
.
It is very convenient for us to calculate the weight distribution. The following corollary can be deduced from Theorem 2.
Corollary 3. Let ![]() be an
be an ![]() linear code over
linear code over![]() , and denote its dual by
, and denote its dual by![]() . Then the dual code
. Then the dual code ![]() is a linear code of length n and dimension
is a linear code of length n and dimension![]() . Let T be a set
. Let T be a set ![]() with
with ![]() and
and![]() , so the weight distribution of
, so the weight distribution of ![]() is uniquely determined. If
is uniquely determined. If![]() , (4) is equivalent to
, (4) is equivalent to
![]() (5)
(5)
It is very convenient to calculate the weight distribution of the dual code![]() . If
. If![]() , we use (4).
, we use (4).
Theorem 4. ( [9] , Th. 1.4.5) Let ![]() be an
be an ![]() linear code over
linear code over![]() , then we have
, then we have
•![]() .
.
•![]() , and
, and![]() .
.
• If ![]() is a binary code, which contains the codeword
is a binary code, which contains the codeword![]() . We know
. We know ![]() for
for![]() .
.
Thus, for a 2-ary linear code![]() , if
, if ![]() contains the codeword
contains the codeword![]() , then the weight distribution of
, then the weight distribution of ![]() is symmetric.
is symmetric.
3. The Parameters of Three Classes of Binary Linear Codes
In this chapter, we construct three classes of binary linear codes based on deep holes, then determine the parameters of these binary linear codes.
Let ![]() be an
be an ![]() linear code over the finite field
linear code over the finite field![]() , let u be a deep hole of the linear code
, let u be a deep hole of the linear code![]() , then we construct general linear code
, then we construct general linear code![]() . We consider binary BCH codes combined with deep holes to construct general linear codes.
. We consider binary BCH codes combined with deep holes to construct general linear codes.
Three classes of binary linear codes are constructed by deep holes combined with the 2-error-correcting binary primitive BCH code and their extended codes, respectively.
Lemma 5. The code E is an ![]() linear code. Suppose u is a deep hole of the code E, and construct general binary linear code
linear code. Suppose u is a deep hole of the code E, and construct general binary linear code![]() . Then the code
. Then the code ![]() is an
is an ![]() linear code, and the dual code
linear code, and the dual code ![]() is an
is an ![]() linear code, where m is odd and
linear code, where m is odd and![]() .
.
Proof. Let ![]() be a basis for a
be a basis for a ![]() -dimensional subspace of
-dimensional subspace of![]() , and the code E is a vector space
, and the code E is a vector space![]() . Since the covering radius of code E is 3, from the definition of deep hole, the maximum error distance
. Since the covering radius of code E is 3, from the definition of deep hole, the maximum error distance![]() . Moreover, the minimum distance of E is 5, it is easy to know that
. Moreover, the minimum distance of E is 5, it is easy to know that![]() . The binary linear code
. The binary linear code ![]() is constructed, we have
is constructed, we have
![]()
Furthermore, we obtain
![]()
so the minimum distance of the linear code ![]() is 3. The binary code
is 3. The binary code ![]() is the vector space
is the vector space![]() . Since
. Since![]() , so the dimension of the linear code
, so the dimension of the linear code ![]() is
is![]() . Namely, the code
. Namely, the code ![]() has parameters
has parameters![]() .
.
Let set ![]() for
for![]() . As
. As![]() , we get
, we get
![]()
and![]() . We denote the minimum Hamming distance of the code
. We denote the minimum Hamming distance of the code ![]() by
by![]() , from the weight distribution in Table 1, we have
, from the weight distribution in Table 1, we have
![]()
Then the dual code ![]() has parameters
has parameters![]() , for odd
, for odd![]() . Therefore, the parameters of the code
. Therefore, the parameters of the code ![]() and of its dual code
and of its dual code ![]() are determined separately.
are determined separately. ![]()
We similarly construct several classes of binary linear codes and determine their parameters. The proof is similar to that of Lemma 5 and is omitted here. These binary linear codes are as follows.
Lemma 6. The code ![]() is an
is an ![]() linear code. Suppose u is a deep hole of the code
linear code. Suppose u is a deep hole of the code![]() . We construct general binary linear code
. We construct general binary linear code![]() . Then the code
. Then the code ![]() is an
is an ![]() linear code, and the dual code
linear code, and the dual code ![]() is an
is an ![]() linear code, where m is odd and
linear code, where m is odd and![]() .
.
Lemma 7. The code ![]() is an
is an ![]() linear code, suppose
linear code, suppose ![]() is a deep hole of the code
is a deep hole of the code![]() . We construct general binary linear code
. We construct general binary linear code![]() . Then the code
. Then the code ![]() has parameters
has parameters![]() , and the dual code
, and the dual code ![]() has parameters
has parameters![]() , for even
, for even![]() .
.
4. The Weight Distributions of Three Classes of Binary Linear Codes
In this part, we determine the weight distributions of these binary linear codes. From the general linear code![]() , the weight distributions of these binary linear codes are related to the coset weight distributions of BCH codes. The coset weight distributions of BCH codes have been studied in the literature [12] [13] .
, the weight distributions of these binary linear codes are related to the coset weight distributions of BCH codes. The coset weight distributions of BCH codes have been studied in the literature [12] [13] .
To facilitate the computation of the weight distribution of the dual code, the following lemma can be deduced.
Lemma 8. Let ![]() be an
be an ![]() linear code, and denote its dual by
linear code, and denote its dual by![]() . Then
. Then ![]() and
and![]() . Thus by Corollary 3, the weight distribution of
. Thus by Corollary 3, the weight distribution of ![]() can be determined by the first d Pless power moments, we obtain
can be determined by the first d Pless power moments, we obtain
![]() (6)
(6)
where ![]() is the number of codewords of weight i in
is the number of codewords of weight i in![]() .
.
Theorem 9. The binary code ![]() is an
is an ![]() linear code, and the dual code
linear code, and the dual code ![]() is an
is an ![]() linear code, where m is odd and
linear code, where m is odd and![]() . Moreover, the weight distribution of
. Moreover, the weight distribution of ![]() is shown in Table 4.
is shown in Table 4.
Proof. Let![]() , as
, as![]() , we have
, we have ![]() if
if ![]() and
and![]() . From Table 1, it is easily seen that the minimum weight distribution of
. From Table 1, it is easily seen that the minimum weight distribution of ![]() is at least 3. Thus, there are three nonzero weights of
is at least 3. Thus, there are three nonzero weights of ![]() as follows:
as follows:
![]()
So the weight of the code ![]() contains
contains![]() . Let
. Let ![]() be the total number of codewords with weight
be the total number of codewords with weight ![]() in
in![]() . In addition, let
. In addition, let ![]() and
and![]() , where
, where![]() . For binary linear codes, then the first three Pless power moments from Lemma 8, we obtain
. For binary linear codes, then the first three Pless power moments from Lemma 8, we obtain
![]() (7)
(7)
where ![]() and
and![]() .
.
By solving this system of equations, we obtain the results in Table 4. The proof is complete. ![]()
Two examples are presented by Magma experiments, which support Theorem 9.
![]()
Table 4. The weight distribution of![]() , for odd
, for odd![]() .
.
Example 1. Let ![]() and let the deep hole vector
and let the deep hole vector![]() , the binary code
, the binary code ![]() has parameters
has parameters![]() . In Theorem 9, the code
. In Theorem 9, the code ![]() is a
is a ![]() binary linear code with the weight enumerator
binary linear code with the weight enumerator![]() .
.
Example 2. Let ![]() and let the deep hole vector
and let the deep hole vector![]() , the binary linear code
, the binary linear code ![]() has parameters
has parameters![]() . In Theorem 9, the code
. In Theorem 9, the code ![]() is a
is a ![]() binary linear code with the weight enumerator
binary linear code with the weight enumerator![]() .
.
Theorem 10. The binary code ![]() is an
is an ![]() linear code, and the dual code
linear code, and the dual code ![]() is an
is an ![]() linear code, where m is odd and
linear code, where m is odd and![]() . Moreover, the weight distribution of
. Moreover, the weight distribution of ![]() is shown in Table 5.
is shown in Table 5.
Proof. Let![]() , as
, as![]() , we have
, we have ![]() if
if ![]() and
and![]() . From Table 2, it is easily seen that the minimum weight distribution of
. From Table 2, it is easily seen that the minimum weight distribution of ![]() is at least 4. Therefore, we know that the code
is at least 4. Therefore, we know that the code ![]() has the following four nonzero weights:
has the following four nonzero weights:
![]()
The weight of the code ![]() contains
contains![]() . Let
. Let ![]() be the total number of codewords with Hamming weight
be the total number of codewords with Hamming weight ![]() in
in![]() , and let
, and let ![]() and
and ![]() for
for![]() . Since
. Since ![]() is even and contains the codeword
is even and contains the codeword![]() . From Theorem 4, we have
. From Theorem 4, we have ![]() and
and ![]() for
for![]() . For the binary linear code, then the first and the third Pless power moments from Lemma 8, we obtain
. For the binary linear code, then the first and the third Pless power moments from Lemma 8, we obtain
![]() (8)
(8)
where ![]() and
and![]() .
.
By solving this system of equations, we obtain the results in Table 5. The proof is complete. ![]()
Two examples are presented by Magma experiments, which support Theorem 10.
Example 3. Let ![]() and let the deep hole vector
and let the deep hole vector![]() , the binary linear code
, the binary linear code ![]() has parameters
has parameters![]() . In Theorem 10, the code
. In Theorem 10, the code ![]() is a
is a ![]() binary linear code with the weight enumerator
binary linear code with the weight enumerator![]() .
.
![]()
Table 5. The weight distribution of![]() , for odd
, for odd![]() .
.
Example 4 Let ![]() and let the deep hole vector
and let the deep hole vector![]() , the binary linear code
, the binary linear code ![]() has parameters
has parameters![]() . In Theorem 10, the code
. In Theorem 10, the code ![]() is a
is a ![]() binary linear code with the weight enumerator
binary linear code with the weight enumerator![]() .
.
Theorem 11. The binary code ![]() is an
is an ![]() linear code, and the dual code
linear code, and the dual code ![]() is an
is an![]() , where m is even and
, where m is even and![]() . Moreover, the weight distribution of
. Moreover, the weight distribution of ![]() is shown in Table 6.
is shown in Table 6.
Proof. Let![]() , as
, as![]() , we have
, we have ![]() if
if ![]() and
and![]() . From Table 3, it is easily seen that the minimum weight distribution of
. From Table 3, it is easily seen that the minimum weight distribution of ![]() is at least 6. Thus, there are six nonzero weights of
is at least 6. Thus, there are six nonzero weights of ![]() as follows:
as follows:
![]()
![]()
The weight of the code ![]() contains
contains![]() . Let
. Let ![]() be the total number of codewords with Hamming weight
be the total number of codewords with Hamming weight ![]() in
in![]() , and let
, and let ![]() and
and ![]() for
for![]() . Since
. Since ![]() is even and contains the code word
is even and contains the code word![]() . From theorem 4, we know that
. From theorem 4, we know that ![]() and
and ![]() for
for![]() . For this binary linear code, then the first, the third and the fifth Pless power moments from Lemma 8 and Corollary 3, we obtain
. For this binary linear code, then the first, the third and the fifth Pless power moments from Lemma 8 and Corollary 3, we obtain
![]() (9)
(9)
where ![]() and
and![]() . Since
. Since ![]() has parameters
has parameters![]() , the minimum Hamming distance is 4, so
, the minimum Hamming distance is 4, so![]() . We need to determine the number of codewords of weight 4 in
. We need to determine the number of codewords of weight 4 in![]() . Since
. Since ![]() is a vector in
is a vector in ![]() but not in
but not in![]() . From Lemma 1, we have
. From Lemma 1, we have
![]()
The minimum distance of ![]() is 6, thus we have
is 6, thus we have![]() , so
, so
![]()
The number of codewords of weight 4 in the coset ![]() is determined in the literature ( [13] , Remark 4), then we obtain
is determined in the literature ( [13] , Remark 4), then we obtain
![]()
Table 6. The weight distribution of![]() , for even
, for even![]() .
.
![]()
Thus, we have
![]()
By solving this system of equations, we obtain the results in Table 6. The proof is complete. ![]()
Two examples are presented by Magma experiments, which support Theorem 11.
Example 5. Let ![]() and let the deep hole vector
and let the deep hole vector![]() , the binary linear code
, the binary linear code ![]() has parameters
has parameters![]() . In Theorem 11, the code
. In Theorem 11, the code ![]() is a
is a ![]() binary linear code with the weight enumerator
binary linear code with the weight enumerator![]() .
.
Example 6. Let ![]() and let the deep hole vector
and let the deep hole vector![]() , the binary linear code
, the binary linear code ![]() has parameters
has parameters![]() . In Theorem 11, the code
. In Theorem 11, the code ![]() is a
is a ![]() binary linear code with the weight enumerator
binary linear code with the weight enumerator![]() .
.
5. Concluding Remarks
In this paper, we consider binary 2-error-correcting BCH codes combined with deep holes to construct general linear codes![]() , where u is a deep hole of the codes
, where u is a deep hole of the codes![]() . Therefore, we not only construct three classes of binary linear codes, but also determine the parameters and the weight distributions of these binary linear codes. Furthermore, we wish to construct more general linear codes related to deep holes.
. Therefore, we not only construct three classes of binary linear codes, but also determine the parameters and the weight distributions of these binary linear codes. Furthermore, we wish to construct more general linear codes related to deep holes.