1. Introduction
Ball lightning is a peculiar natural phenomenon that does usually appear during thunderstorms as a spherical and freely moving luminous entity. Its scientific study began during the first decades of the 19th century, when Arago [1] gathered about 30 witness accounts. Actually, he was motivated by stories about “stones that fell from the sky”. They were attributed to unreliable witnesses, since that seemed to be impossible. These observations did not only concern meteorites. “Fire balls” were also reported. They seemed to be a particular form of lightning, but were also treated with skepticism. Even today, the preconception that BL cannot be real, has not yet completely disappeared. It was suggested, indeed, that ordinary lightning could create round afterimages [2] or that the strong transient magnetic field could stimulate the brain and produce phosphenes [3] . Are these propositions sufficient to explain several thousand collected witness reports and the actually observed properties of the luminous balls? Arago preferred to get better knowledge of the phenomenon than to speculate.
Sauter [4] , a German high school teacher, collected and analyzed 213 witness accounts from before 1895. About 15 years later, the Belgian scientist De Jans [5] provided a larger sample of observations. Trying to understand these facts, he noted that several authors had proposed a chemical interpretation, by assuming the existence of some yet unknown type of “fulminate matter”. However, he was convinced that “BL is essentially an electrical phenomenon”. He mentioned, but rejected the proposition that BL could be a spherical condenser [6] , since a static separation of positive and negative charges is impossible in atmospheric air. That is true, but we will show that a condenser-like charge separation can be achieved in a dynamical way.
Brand [7] , another German high-school science teacher, published in 1923 a very remarkable study, based on a collection of about 600 written reports. He selected 215 cases and provided a full copy of these observations. His careful analysis confirmed not only the existence of BL, but extended also the repertoire of its amazing properties. Nevertheless, no plausible theoretical proposition emerged until the famous Russian physicist Kapitsa [8] compared BL in 1955 to the bright luminous spheroid generated by nuclear explosions. It has a diameter of about 150 m and contains totally ionized air, but radiates all its energy in less than 10 s, because of rapid recombination processes. Since light emission is proportional to the surface and since the diameter of BL is of the order of 10 cm, its lifetime should be about 5 × 10−6 s. Actually, it is of the order of a few seconds and can even reach some minutes. BL does thus require an energy input.
Kapitsa suggested that these plasma balls might absorb energy from EM radiation that is present in the terrestrial atmosphere under thunderstorm weather conditions. This hypothesis was not confirmed, but Kapitza’s rational approach and the fact that the BL phenomenon merits scientific research arose much interest. Further milestones of BL research were the books of Singer [9] , Barry [10] and Stenhoff [11] , as well as review articles of Smirnov [12] and Turner [13] . Since microwaves can ionize air and set electrons in oscillation, they are able to create luminous plasmoids [14] . They resemble BL, but have more irregular boundaries and BL is not created in microwave ovens. Many reports about other BL observations, their analysis and new theoretical propositions continued to appear.
The present article is a modified version of a presentation at the International Symposium on Ball Lightning (ISBL) in Kaliningrad, Russia, 2010. It was published in the Proceedings [15] . Section 2 is devoted again to providing information about literature and phenomenology. Its analysis could be helpful, indeed, to detect clues for the construction of a theory that explains the observed facts. Section 3 justifies the theory proposed in 2010 in a simpler way. Section 4 is devoted to applications of this theory. They show that many strange facts can now be explained in a rational way. Eventually, some conclusions can be drawn from this approach, even in regard to scientific methodology.
2. Analysis of Phenomenological Data
2.1. Formation and Appearance of BL
Observations of BL are by far the most frequent during thunderstorm activity, especially towards its end [7] . This suggests that BL contains charged particles, resulting from increased ionization of atmospheric air. Moreover, BL appears often a short time after a lightning strike and quite close to its impact. Since linear lightning produces a strong magnetic field of short duration, we have to expect that this field could contribute to the natural production of BL. However, witnesses tell us that the luminous entity did suddenly appear in front of their eyes, as if a light bulb had been switched-on. Before this happened, they saw nothing special at this place, but we will show that “invisible BL” is also possible. It was already present in a virtual state, before it became visible.
An essential property of BL is that, once it reaches its light emitting state, it does usually preserve the same size, color and luminosity during its whole lifetime. This constancy implies a mechanism that has several functions. It concentrates positive and negative charges to get an electrically neutral plasma. The light electrons are there set in collective oscillation with respect to the heavier ions. These oscillations are even sustained, in spite of inevitable energy losses and constant reduction of the number of charged particles by recombination processes. This requires to capture positive and negative charges that are present at lower densities in the ambient medium. Like living beings, BL is a dissipative system that survives as long as possible by interacting with its environment. According to Prigogine, this results from nonlinear equations, but they were not obvious for BL.
Nikitin mentioned also that nonlinear equations are required [16] , but how this idea should be implemented remained an unsolved problem. Living beings are endowed with special faculties, transmitted by means of DNA. BL is much simpler, but also able to survive in a thermodynamically unstable excited state. It is even able to resist a wide range of changing conditions. Silberg [17] considered already in 1978 a nonlinear current-voltage relation for the generation of BL in submarines. Sanduloviciu et al. [18] presented experimental evidence for spatial structuring of low-pressure plasmas, associated with nonlinear current-voltage characteristics. Dimitriu et al. extended this work [19] and showed that nonlinear responses of electrons and ions to electric fields can create luminous dipole layers. However, BL does not result from applying an electric field and requires no low-pressure gas. The Russian plasma physicist Kadomtsev [20] tried also to relate BL to a nonlinear current-voltage relation. Even the unaltered propagation of nerve-impulses along axons depends on nonlinear effects, regulating the conductivity of biological membranes for different types of ions. To prove that BL results from processes that lead to nonlinear equations, we need more relevant data. It is also necessary to decode messages that result from observations and could be helpful to discover what might explain the unsolved mysteries.
2.2. Motions, Disappearance and Energy Content of BL
BL is usually moving in an erratic way. It tends even to enter into a house and seems to explore it, before leaving it through open doors or windows. It is more reasonable, of course, to assume that BL is moving around since it is searching charged particles. They are present in atmospheric air, especially during thunderstorm activity, but their density can be greater in a house than in open air. The idea of inhomogeneous distributions of charged particles is confirmed by the fact that BL can move against wind. Sometimes, it does even squeeze itself through key-holes or narrow slits. It is thus reasonable to assume that it is attracted by the presence of more charged particles on the other side.
Since BL can even pass through window panes that remain intact [21] , it is also necessary to abandon the idea that BL is a material object. The plasma membrane is even not constituted of a special type of atoms or molecules. It is merely atmospheric air, but the density of charged particles is there greater than elsewhere and they are in an excited state that is metastable. We may presume that BL is luminous, since it is a “fire ball”. We are even accustomed to the concept of a hot plasma, as in an electric arc or the Sun, but BL is different. Indeed, when freely moving BL passed near witnesses, they did not notice any heat radiation. BL is thus a plasma that can exist and even subsist some time at normal atmospheric temperature. Why?
Instead of considering only chaotic motions and random collision of charged und neutral particles, we may have to accept the possibility of precisely orchestrated motions of all unbound electrons inside the plasma membrane. Such “plasma oscillations” are known to exist in solid-state physics, but escaped attention of scientists who studied the BL phenomenon. Moreover, the concept of collective motions of unbound electrons in the plasma membrane of BL is not implemented in the same way as for conduction electrons in small metal particles or thin metal films. The objective of this article is to make mentally visible what is essential, but hidden to direct perception.
It is thus necessary to begin with analyzing observed facts, since they define what is real or not. They could also help us to discover useful hints for constructing a theory that might explain in a logical and coherent way what could be observed, but remained very mysterious. It is paradoxical, for instance, that BL can disappear in two very different ways. It can vanish by silent “extinction”, as if a light bulb had been switched-off, or end its existence with a loud and often very violent “explosion”. According to some statistics [12] , the probabilities are nearly equal. How does this come about?
It is customary to assume that the liberated energy was stored inside the luminous entity. In some cases, it was even possible to evaluate this energy content. The observation of Morris in 1936 provides an instructive example [9] [10] [11] . He saw a luminous red ball that had only the size of an orange, but when it entered a barrel that contained about 18 liters of water, this water was heated to boiling temperature and evaporated. This led to the conclusion that this BL contained an energy density of about 6 × 103 J/cm3. Some 30 workers of a Hungarian factory observed in 1972 a BL of a football’s size that entered a water pit. This was already astonishing, but became even more surprising when it led to the complete evaporation of about 120 liters of water [22] . This would require an energy density of about 3 × 104 J/cm3. Many other evaluations were made [10] . They included also an interaction with wood that may have been humid.
2.3. Statistics for Diameter, Lifetime and Luminosity
Much effort was devoted to establish statistical data by collecting and analyzing witness reports. It appeared that different collections displayed no systematic differences and that the probability distribution P(X) is very similar for different observables X. This can be the estimated diameter of BL, its lifetime, luminosity or velocity of displacement. There is always a most probable value for X, but the distribution is skewed, so that larger values of X are more frequent than smaller ones. Nevertheless, the most probable diameter falls between 10 and 50 cm (for 63% of 4587 cases), while the diameter was smaller than 2 cm or larger than 1 m in about 2% of this ensemble [23] . The size of BL was often compared to that of an orange, a child’s head or a football, for instance. However, BL can be as small as a pea or very big [24] .
Dijkhuis [25] has proven in 1992 that all existing data collections are compatible with a unique probability distribution P(X). It turned out to be a log-normal distribution. This means that one gets a normal, bell-shaped distribution when logX is considered as the random variable instead of X. To optimize the comparison with empirical data, Dijkhuis used the cumulative probability distribution, renormalized in terms of the corresponding average value and standard deviation [11] . The most probable values are then nearly 19 cm for the diameter, 8 s for the lifetime, 70 W for the luminosity and 1 m/s for the velocity of displacement. The arithmetically calculated average values would be greater, of course. This summarizes a century of data collection on three continents and is the only quantitative law in this field. Though this is a statistical law for a large ensemble of observations, it is important, since it should be possible to explain this remarkable fact.
Grigorjev et al. noted already that bigger BL tends to have a longer lifetime and a greater luminosity [26] . Amirov and Bychkov [27] confirmed that lifetime and diameter increase together, but they noted a special feature. The correlation is related to the mode of disappearance. For exploding BL, the lifetime decreases beyond a certain value of the diameter, while this is not true for extinctions. In our view, bigger BL requires a greater number of charged particles. This number has even to be increased to cause explosions, while extinctions do simply follow from a lack of charged particles.
2.4. Two Possible Structures of BL
It would be very helpful to know more about the internal structure of BL, but in general, we ignore if light is only generated in a relatively thin membrane at the surface of BL or also in its volume. We will thus consider both hypotheses, but the following observations are in favor of the first one. In 1904, a German engineer and his wife were walking in stormy weather. There was rain, hail, snow and strong wind. Nevertheless, they saw a luminous ball that had a diameter of about 4 m. It sank to the ground and for a short while, it enveloped the couple [28] . They were not harmed, but were isolated from the outside wind and stood in a thick white sea of light. They had no sensation of heat and did not perceive any odor, but were surrounded by a luminous membrane. It was not perfectly transparent, since it allowed only to see nearby pebbles on the road [9] .
During a violent electrical storm in 1895, there appeared a distinctly outlined yellow-red sphere that had the apparent size of the moon. “Its outer rim appeared to be a fine, bright ring, as if the sphere had a skin”. It disappeared with a mighty detonation when it collided with a cottage and destroyed it [29] . Grigorjev et al. found that in 226 cases among 2082 observations (11%), the witnesses mentioned that BL had a semi-transparent shell [21] . The luminous plasma can thus be confined to a membrane. However, the external surface of BL is not necessarily smooth.
A floating luminous ball with a diameter of about 15 cm had the appearance of a soap bubble, but it was covered with a 2.5 cm thick semi-transparent furry coat. The witness could see through this layer and saw that the inner face of the opposite side was smooth [30] . Since the external surface carried here and there some spikes that had a length of about 5 cm and since their positions changed all the time, charged particles had also to be constantly renewed in the membrane of these cylindrical extrusions. This BL disappeared with a loud pop that produced ozone. Spherical BL can even display quite long radial protrusions. It happened also that moving BL had a tail that remained visible some time. This fact suggests that minute particles were formed and left behind, since they would cause Rayleigh scattering of incident light. This is confirmed by the fact that the mist was blue in reflected light and brown in transmitted light [7] .
“Hollow balls” were also reported [7] , but it is particularly noteworthy that some witnesses saw a “luminous core with a halo” or even several concentric luminous shells. The Russian chemist Dmitriev made in 1967 a very remarkable observation of this type [31] . He saw a BL that appeared after an intense flash of ordinary lightning and moved toward the observer. He was camping at the Onega River and specialized in studying the composition of air [9] . He saw that the luminous ball was slightly ellipsoidal. The vertical axis would be 14 cm for an average radius of 13 cm. This BL had a very bright central part of yellow-white color, surrounded by two luminous shells. They were easily discernable, since the middle shell was dark violet and the outer one light blue. They had a thickness of about 2 cm, while the core had a diameter of 6 to 8 cm. This luminous ball appeared above the river and approached the witness by following the curved path of assembled wood floats. Over the shore, its motion became erratic and disappeared after contact with a tree. Although it was not very great, the life-time of this BL amounted to about 80 s. This unusual duration was probably due to a high ionization level of the ambient air at that place and that time.
The chemist was equipped with evacuated 200 cm3 glass bulbs, to collect air samples for later analysis. He did this at intervals of 5 seconds when the plasma ball was passing close to him. The tubes were held over his head. There was “a visible trail of bluish mist with an acrid odor”. The scientist had the impression that “energy was continually generated in the lightning ball”, since he heard a continuous crackling noise. His transistor receiver detected also a “continuous rumble”. This BL did thus produce some audible sound and even EM waves at radio frequencies. However, in both cases, the intensity and frequency were randomly changing. Later analysis of the gas samples disclosed that the concentrations of all air components were normal, except for a strong increase of O3 and NO2 between taking the first and second sample. The third sample indicated a slow decrease, but the concentrations where nearly normal again in the fourth sample. This leaves no room for doubting the presence of charged particles inside and near BL.
BL is frequently moving at a height of about 1 or 2 m above the ground at a velocity that is similar to that of a walking man, but there is no general rule. Even fast motions from clouds towards the ground have been observed. The path can be oblique with respect to wind. BL can also remain motionless for some time, as if it were mysteriously attached to something [7] . It can roll along wire fences, rain gutters, telephone wires, power lines or the extension cord of a table lamp. This indicates that BL is attracted by metallic conductors. We mentioned already that free-floating BL radiates no heat. However, direct contact with metallic wires can melt them. A gold wedding ring got then very hot. On contact with moist ground, BL can dig a furrow, like an excavator [32] . It is paradoxical, of course, that BL can be cool or very hot and powerful. How that is possible, has to be explained, of course.
BL is usually soundless, but can produce hissing, buzzing or crackling noises. The emitted light can have various colors. For more than 4000 events [12] , the most frequent colors were orange (23%), white (21%) and yellow (20%), followed by red and pink (18%), blue or violet (11%). Green was rare (1%), but patches of different colors were also possible (6%). The external surface of BL can carry wormlike structures [33] . They seem to be randomly breaking up and reconstituted. Changes of color and size were sometimes observed immediately before silent or explosive disappearance [10] . We interpret this fact as resulting from the beginning of an important decrease or increase of the content of charged particles in the luminous membrane.
During the apparently erratic motions of BL the intensity of the emitted light can fluctuate. Still photographs did even document quite regular extinctions and reappearances along a trajectory with many curves [10] . Since these pulsations were not visually detected, their frequency was higher than about 20 Hz. This fact suggests that the density of available charged particles was not sufficient for constant emission of light. Some witness did even perceive momentary extinctions [34] , but the light reappeared again. BL is thus also able to survive as a virtual entity.
Usually, BL has a spherical form that has to result from some type of surface tension. BL can even bounce on the ground like a rubber ball. Though surface tension suggests that the external surface should be as small as possible, it can be enlarged by radial protrusions. Even rod-shaped and snake-like BL have been observed [35] . When spherical BL is hovering over a tree or a church tower, it can fall apart in many smaller globes. However, two modest spheres can also fuse to yield a bigger entity. Even a flat rectangle has been reported [35] . We have thus to conclude that the central difficulty of the BL problem does not result from a lack of information, but from a wealth of data of bewildering complexity and undisputable originality. To understand this phenomenon, we have to crack the code. For an excellent review that includes also attempts to explain the BL phenomenon, we refer to Donoso et al. [36] . Let’s now try to construct a theory that explains the baffling variety of observed facts. This endeavor requires to imagine what is hidden, but has to account for those facts that could be observed by means of logical reasoning and well-established physical laws.
3. Theory of Electronic Plasma Oscillations in BL
3.1. Natural Formation of Luminous Plasma Bubbles
It occurs when atmospheric air is ionized, because of thunderous weather. Charge separation is then occurring in cumulonimbus clouds. Their bottom is negatively charged, while the surface of the Earth is positive. The resulting electric field is vertical and oriented upward. The lower atmosphere contains always some free electrons, created by cosmic rays. Because of the atmospheric electric field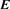 , they move toward the ground. They can even be accelerated so much that they cause an avalanche of ionization processes, as shown in Figure 1(a). The density of unbound electrons (e−) and ions (X+) can thus lead to the formation of a local plasma cloud. The charged particles tend there to be uniformly distributed to ensure electrical neutrality, since energy is then minimal.
, they move toward the ground. They can even be accelerated so much that they cause an avalanche of ionization processes, as shown in Figure 1(a). The density of unbound electrons (e−) and ions (X+) can thus lead to the formation of a local plasma cloud. The charged particles tend there to be uniformly distributed to ensure electrical neutrality, since energy is then minimal.
However, any force field that acts on all charged particles inside this plasma cloud will provoke a collective displacement of unbound electrons with respect to the heavier positive ions. Since they remain practically at rest, there appear positive and negative surface charges. This is the initial state of BL, represented
![]()
Figure 1. Formation of Ball Lightning. (a) Local ionization, triggered by one accelerated electron. (b) A perturbation displaces all unbound electrons in the resulting plasma cloud. The surface charges compress the cloud and initiate collective oscillations. (c) Formation of an invisible BL with a closed membrane and transverse oscillations of all unbound electrons. (d) These oscillations can be amplified and sustained by interacting with the surrounding air, to yield luminous BL.
in Figure 1(b). A sudden modification of the atmospheric electric field is sufficient, but BL does usually appear shortly after a lightning strike and not far from its impact on the ground. Linear lightning is equivalent to a very intense electric current of short duration. It creates thus a transitory magnetic field B. Its circular field lines are usually horizontal. Combined with the vertical electric field E near the surface of the Earth, it yields a short, but strong EM pulse that pushes all moving electrons sideways in the plasma cloud. The resulting positive and negative surface charges attract one another and will thus flatten the plasma cloud as much as possible. It could become a plate of limited extension, but a closed membrane is more stable. The surface charges create an electric field inside the compressed plasma cloud. All unbound electrons were displaced together and will move together to restore equilibrium, but like a pendulum, they exceed this goal.
The perturbation did thus also initiate collective oscillations of all unbound electrons inside the plasma membrane. These oscillations are radial for a spherical shell, as indicated in Figure 1(c). When these motions are not yet strong enough to excite neutral atoms and molecules, this yields invisible BL. It can become visible somewhat later at another place. This requires that the plasma oscillations lead to collisions that produce light emission. Figure 1(d) shows a central section through visible BL and its membrane. It is luminous, since the kinetic energy of the oscillating electrons is great enough to excite neutral particles. Because of inevitable energy and particle losses, the oscillations have to be sustained. They had even to be amplified to transform invisible BL into visible one. The originality and beauty of the BL phenomenon is that this can be achieved in a remarkably efficient way.
3.2. Collective Oscillations of Electrons in Plasma Membranes
The first required step is now to understand why synchronized oscillations of all unbound electrons are possible in a plasma membrane. A small portion of the membrane can be treated as if it were flat. The unbound electrons and positive ions are there homogeneously distributed, but Figure 2(a) shows that when all these electrons are displaced by a distance u, there appear surface charge densities , where
, where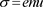 . As in charged condensers, planar surface charges create a homogeneous electric field E. Its magnitude is
. As in charged condensers, planar surface charges create a homogeneous electric field E. Its magnitude is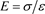 , where
, where  is the dielectric constant of the membrane. For unpolarized air molecules, we would get
is the dielectric constant of the membrane. For unpolarized air molecules, we would get . The electric field E has the same orientation as the displacement u of the electrons. It points towards the right side of the membrane, but every unbound electron is subjected to the force −eE. It acts like a restoring force for a harmonic oscillator, but the oscillations should be attenuated because of friction. The average braking force is then proportional to the velocity. The equation of motion for any one of the unbound electrons inside the membrane is thus
. The electric field E has the same orientation as the displacement u of the electrons. It points towards the right side of the membrane, but every unbound electron is subjected to the force −eE. It acts like a restoring force for a harmonic oscillator, but the oscillations should be attenuated because of friction. The average braking force is then proportional to the velocity. The equation of motion for any one of the unbound electrons inside the membrane is thus
 where
where 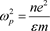 (1)
(1)
Every dot corresponds to a derivation with respect to the time variable t. The parameter  is the collision frequency of the electrons. It should be noted that even if the electrons were only deviated from their normal path, that would already be equivalent to a loss of kinetic energy along the direction of the electric field. Actually, the colliding electrons cause vibrations and heating, but BL remains cool. This observation indicates already that the term
is the collision frequency of the electrons. It should be noted that even if the electrons were only deviated from their normal path, that would already be equivalent to a loss of kinetic energy along the direction of the electric field. Actually, the colliding electrons cause vibrations and heating, but BL remains cool. This observation indicates already that the term 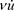 can be abolished. We will prove that by means of Figure 2(b). At present, it is only important that when the second term of the equation of motion (1) vanishes, its solution is
can be abolished. We will prove that by means of Figure 2(b). At present, it is only important that when the second term of the equation of motion (1) vanishes, its solution is 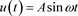 for an adequate choice of the instant
for an adequate choice of the instant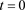 . Of course,
. Of course, . This is the so-called “plasma frequency”. Its value depends on the density n of unbound electrons in the membrane.
. This is the so-called “plasma frequency”. Its value depends on the density n of unbound electrons in the membrane.
The author of this article met the concept of plasma waves already long ago. As a young professor, teaching quantum mechanics and solid-state physics, he knew that the interaction of a photon with an electron requires a “third body” for energy and momentum conservation. This yields specific surface effects and
![]()
Figure 2. (a) In a plasma membrane, all unbound electrons can be displaced by a distance u with respect to the positive ions. This produces surface charge densities ±σ and an electric field inside the membrane. The resulting restoring force causes harmonic oscillations. (b) A swing and a pendulum are similar systems, but energy losses by air friction can be compensated by simply modifying the length L in a special way.
at the University of Marseille, several teams of physicists were measuring the optical properties of thin metal films. They were said to be “anomalous”, since they could not be explained by means of known theories. Actually, they used thin films, resulting from condensation of metal vapor on transparent substrates. This yields minute metal islands and thus more surface effects. Metals contain conduction electrons and positive ion cores. They form a lattice and can be assumed to be at rest at the time scale of electronic motions. The conduction electrons are similar to unbound electrons in the plasma membrane of BL, but damping cannot be abolished for thin granular metal films.
On the contrary, when the conduction electrons are set in forced oscillations by the electric field E of an electromagnetic wave, they cause absorption by giant resonance effects when the frequency ω of the EM wave is close to plasma frequency ωp of the metal particle. The actual size of this particle is irrelevant, but it has to be small, to yield only dipolar oscillations. The resonance is huge and broad, because of energy losses that are caused by collisions of the conduction electrons with ion cores. The observed anomalies could thus be explained [37] . Creation of “surface plasmons” was already known to account for characteristic energy losses when electrons pass through very thin metal foils [38] . It was also known that continuous metal films produce very peculiar optical effects [39] . The optical properties of granular metal films were special. When we became aware of the mysterious BL phenomenon, we thought that gaseous plasma balls could also allow for plasma oscillation. However, they have outstanding properties, since energy losses by friction can be abolished.
3.3. A Simple Way to Overcome Attenuation
Any swing or pendulum is a harmonic oscillator, since the mass M is constantly subjected to the gravitational force Mg, but only its component along the possible path is relevant. This path is determined by the fact that the mass M is suspended on a string of constant length L. For small angular deviations, the equation of motion is then
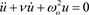 where
where 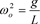 (2)
(2)
The parameter  accounts for air friction. Even a child, sitting on a swing, needs thus a regular push by another person, but by trial and error we found a way to sustain the oscillations without external help. Pushing with the feet on the ground is sufficient to initiate the oscillations. They could then be amplified by changing position in a regular way. It was sufficient to sit upright near both extremities of oscillatory motions and to adopt a flat position at the bottom. This was equivalent to raising the center of mass and adding potential energy, every time when the kinetic energy was low. Trapeze artists use the same method to amplify oscillations. To understand what happens in a more detailed way, it is essential to realize that the trajectory of the mass M of the pendulum has to be similar to the interrupted line in Figure 2(b). It is an 8-like curve that can be approximated by considering that the length L of pendulum is modified so that
accounts for air friction. Even a child, sitting on a swing, needs thus a regular push by another person, but by trial and error we found a way to sustain the oscillations without external help. Pushing with the feet on the ground is sufficient to initiate the oscillations. They could then be amplified by changing position in a regular way. It was sufficient to sit upright near both extremities of oscillatory motions and to adopt a flat position at the bottom. This was equivalent to raising the center of mass and adding potential energy, every time when the kinetic energy was low. Trapeze artists use the same method to amplify oscillations. To understand what happens in a more detailed way, it is essential to realize that the trajectory of the mass M of the pendulum has to be similar to the interrupted line in Figure 2(b). It is an 8-like curve that can be approximated by considering that the length L of pendulum is modified so that
![]() when
when ![]()
For small values of α, Equation (2) is thus modified so that
![]() (3)
(3)
The last term of Equation (1) becomes then
![]()
This implies a nonlinear effect, since the product of two oscillating functions is equal to the sum of two other oscillating functions. It appears now that the small periodic modulation of the length L is equivalent to creating two additional forces. One of them can precisely compensate air friction in (1), since ![]() . It is therefore sufficient to adapt the value of α so that
. It is therefore sufficient to adapt the value of α so that![]() . The oscillations can even be amplified when
. The oscillations can even be amplified when![]() . It should be noted that the other force has negligible effects, since the frequency 3ω is off-resonance. Such a system is called a “parametric amplifier”, since it overcomes friction by merely modifying one parameter. This effect can by demonstrated by means of a simple experiment. The length L of the pendulum is modulated by regular traction and relaxation with the adequate timing. The enigmatic BL phenomenon can be elucidated by transposing this method. Surprisingly, that is possible.
. It should be noted that the other force has negligible effects, since the frequency 3ω is off-resonance. Such a system is called a “parametric amplifier”, since it overcomes friction by merely modifying one parameter. This effect can by demonstrated by means of a simple experiment. The length L of the pendulum is modulated by regular traction and relaxation with the adequate timing. The enigmatic BL phenomenon can be elucidated by transposing this method. Surprisingly, that is possible.
3.4. BL Is an Autonomous Parametric Amplifier
After the initial ionizations that created a local plasma cloud (e− and X+) and the perturbation that displaced all unbound electrons in this cloud, the plasma oscillation was accompanied by other processes. Here is their enumeration:
1) Energy losses by collisions of oscillating electrons with heavier particles.
2) Energy losses of electrons, by exciting bound electrons, followed by light emission.
3) Electron attachment to neutral particles, producing negative ions (![]() ).
).
4) Recombination of electrons and positive ions (![]() ).
).
5) Dissociation of negative ions (![]() ).
).
6) Recombination with positive ions (![]() ).
).
7) Capture of e− and Y− from the outside medium when the surface of BL is positive.
8) Capture of X+ from the outside medium when the surface is negative.
The density n of unbound electrons, the density x of negative ions and the density N of positive ions do thus vary in the following way:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
The coefficient a accounts for the probability of attachment of an electron per unit time. Every attachment to a neutral particle produces a negative ion and in atmospheric air, this results from collisions of electrons with oxygen molecules (![]() ). The actual probability of attachment depends thus also on the kinetic energy of the electrons. It is proportional to the square of the velocity v of the electrons. The second term of Equation (4) determines the rate of electron losses by recombination, while the third term defines the rate of extracting electrons from the external medium when the surface charge density is positive. The second term of (5) specifies the loss of negative ions by dissociation and recombination with positive ions. The third term accounts for the extraction of negative ions from adjacent air. Equation (6) relates the loss of positive ions to their increase, by extracting new ones from external and internal air when the surface charge of the membrane is negative. It is important that for light emission, it is sufficient to excite air molecules inside the membrane. The electrons do thus not have to reach the high energies that would be required for ionization (12.1 eV for O2 and 15.5 eV for N2). However, excitations result from inelastic collisions and will thus increase frictional damping. This is precisely what can be compensated by parametric amplification. How can this be achieved for BL?
). The actual probability of attachment depends thus also on the kinetic energy of the electrons. It is proportional to the square of the velocity v of the electrons. The second term of Equation (4) determines the rate of electron losses by recombination, while the third term defines the rate of extracting electrons from the external medium when the surface charge density is positive. The second term of (5) specifies the loss of negative ions by dissociation and recombination with positive ions. The third term accounts for the extraction of negative ions from adjacent air. Equation (6) relates the loss of positive ions to their increase, by extracting new ones from external and internal air when the surface charge of the membrane is negative. It is important that for light emission, it is sufficient to excite air molecules inside the membrane. The electrons do thus not have to reach the high energies that would be required for ionization (12.1 eV for O2 and 15.5 eV for N2). However, excitations result from inelastic collisions and will thus increase frictional damping. This is precisely what can be compensated by parametric amplification. How can this be achieved for BL?
The required energy is provided by extracting charged particles from the ambient medium, since their existence resulted from ionization, requiring energy. The very light electrons are attracted by the surface charge density ![]() on the external side of the plasma membrane. It varies at the rhythm of the collective oscillations of unbound electrons inside this membrane. It is thus alternatively positive and negative, but we should not forget that the membrane contains high density of electrons and ions. Some of them diffuse through the inner surface and will then be homogeneously distributed in the enclosed air. Instead of merely accumulating ions and unbound electrons, this reservoir offers the possibility to retrieve them. When the external surface is positive, it extracts unbound electrons and negative ions from the ambient air, but the inside surface is then negative and attracts positive ions. Flat luminous plates were rarely observed, but they are possible. In this case, it is obvious that intake of charged particles occurs at both sides, but that is also possible for a closed plasma membrane. Even for a pendulum, perfect symmetry of energy injection is not required, but simplifies the theoretical treatment. Let us assume that the surface charge densities
on the external side of the plasma membrane. It varies at the rhythm of the collective oscillations of unbound electrons inside this membrane. It is thus alternatively positive and negative, but we should not forget that the membrane contains high density of electrons and ions. Some of them diffuse through the inner surface and will then be homogeneously distributed in the enclosed air. Instead of merely accumulating ions and unbound electrons, this reservoir offers the possibility to retrieve them. When the external surface is positive, it extracts unbound electrons and negative ions from the ambient air, but the inside surface is then negative and attracts positive ions. Flat luminous plates were rarely observed, but they are possible. In this case, it is obvious that intake of charged particles occurs at both sides, but that is also possible for a closed plasma membrane. Even for a pendulum, perfect symmetry of energy injection is not required, but simplifies the theoretical treatment. Let us assume that the surface charge densities![]() , where
, where
![]() when
when ![]() (7)
(7)
These functions are represented in Figure 3 and play an essential role for the BL phenomenon. The red curve yields the first term of a Fourier expansion of ![]() and
and![]() .
.
The previous article [40] did correctly account for the surface charge densities ![]() and for kinetic effects of electron attachment inside the membrane. To be more explicit, we note that Equation (4) contains two oscillating functions, since
and for kinetic effects of electron attachment inside the membrane. To be more explicit, we note that Equation (4) contains two oscillating functions, since
![]()
Figure 3. The oscillating collective displacement u(t) of unbound electrons in a plasma membrane (blue line) leads alternatively to positive and negative surface charge densities. The intake of electrons is thus regulated by the function σ(t). It is also oscillating, but does vary at a different pace (red line).
![]()
The density n of unbound electrons varies thus so that
![]()
On the average, the electron density n can thus remain stationary, but also increase or decrease in an exponential way. Anyway, there is an oscillatory modulation, since
![]() (8)
(8)
Since BL has a strong tendency to be electrically neutral, the densities ![]() do usually have average values
do usually have average values![]() , so that
, so that![]() . For a stationary state, the loss of electrons inside the membrane (by recombination and increased attachment) has to be compensated by electrons, coming from the ambient atmospheric air and the compressed charges inside the plasma bubble. We get then
. For a stationary state, the loss of electrons inside the membrane (by recombination and increased attachment) has to be compensated by electrons, coming from the ambient atmospheric air and the compressed charges inside the plasma bubble. We get then
![]() where
where ![]()
The value of B depends on the amplitude and frequency of collective oscillations of all unbound electrons inside the membrane. They are also constants for a stationary state and the solution
![]() where
where ![]()
The plasma frequency ![]() in Equation (1) is then precisely modulated like
in Equation (1) is then precisely modulated like ![]() in Equation (2). This means that plasma oscillations can be sustained in BL, but not only by extracting charged particles from the external and internal medium. Even the increased attachment of electrons inside the plasma membrane because of kinetic effects does contribute to parametric amplification. It is required to overcome damping, which results from energy and charged particle losses. We will show in Section 3 that the concept of plasma oscillations and their parametric amplification do also explain astounding properties of BL when it interacts with water, metals and glass.
in Equation (2). This means that plasma oscillations can be sustained in BL, but not only by extracting charged particles from the external and internal medium. Even the increased attachment of electrons inside the plasma membrane because of kinetic effects does contribute to parametric amplification. It is required to overcome damping, which results from energy and charged particle losses. We will show in Section 3 that the concept of plasma oscillations and their parametric amplification do also explain astounding properties of BL when it interacts with water, metals and glass.
Even when BL is merely surviving in atmospheric air (much longer than expected), it is already necessary to explain the possible existence of a metastable state. It results from (8) and implies that BL is functioning like a clockwork, since everything fits together to insure coordinated action. This mechanism may seem to be miraculous, but life emerged also from natural processes. This could even happen in an independent way on many planets in our Universe. Research has to continue in this regard and also for BL, but the DNA of this phenomenon resides in plasma oscillations. We note also that the proposed theory accounts for the fact that BL can be electrically neutral on the average to minimize the total energy, but its total electric charge
![]() (9)
(9)
V is the volume of the plasma membrane. The oscillation of the electric charge will be helpful to understand other properties of BL in special situations. Moreover, BL is not only a parametric amplifier, but an autonomous one. It moves around to find the charged particles that it needs for survival by attracting close ones, but is also attracted itself towards greater densities of charged particles. The most important result is that the basic problem of the BL phenomenon, clearly recognized by Kapitsa in 1955, is now solved. This was only possible by considering plasma oscillations [41] . The essential process is analogous to the respiration of living systems, extracting oxygen molecules from the ambient medium in a periodic way. We may thus call it “inhalation”. Fishes are able to use oxygen molecules that are present in water. Terrestrial animals need special respiratory organs, while BL does merely use electrical means. This applies as well to invisible as to visible BL.
3.5. Concentric Plasma Bubbles
The thickness of plasma membranes is irrelevant for collective oscillations of unbound electrons in spherical or nearly spherical BL. The actual shape is determined by surface tension effects and heavier particles in the enclosed air. Even the local composition of the plasma membrane can be different, since its color is not always homogeneous. It is more surprising that BL can have a layered structure, but this fact is well established by the observations of Dimitriev [33] . He saw a very luminous white core, surrounded by a blue shell and an intermediate purple layer. Other witnesses saw only a luminous core that was surrounded by what they described as a separate halo.
These facts are comprehensible, since the formation of BL could occur at a place where the density of charged particles was sufficiently high and distributed so much that a single plasma membrane was not sufficient to harbor them. The perturbed plasma cloud can then lead to standing plasma waves inside a spherical or spheroidal volume [40] . However, it is simpler and sufficient to consider only concentric plasma bubbles. The luminosity and color of emitted light is then determined by the density and kinetic energy of the colliding electrons in separated plasma membranes.
3.6. Rod-Shaped BL Ribbons and Radial Extensions
Cylindrical BL with rounded extremities has been observed ( [33] , p. 119). The length of luminous rods ranges from about 2 m to 7 m. Even a grayish “torpedo-shaped body” was seen at a distance of about 100 m. Its length and diameter were respectively estimated to be close to 2 m and 20 cm. The ratio 10/1 was reduced for instance to 3/1 for smaller rods. In another case, the baffled witnesses saw that a luminous “ring” detached itself from a spherical light ( [33] , p. 102). It behaved like ripples of water when a stone is thrown into water. As soon as the expanding ring vanished, it was followed by a second ring, less bright than the first one. This indicates that the ambient air was very ionized. Even a luminous ribbon was observed during a storm ( [33] , p. 151). This “magnificent thing” was attached to a luminous object of about 20 cm. Though this “tail” was crinkled like a silk ribbon, it reached a length of about 1 m. The formation of rod-like BL or ribbons depends of course on the shape of the initial plasma cloud. Spherical or spheroidal BL is more probable. When rod-shaped BL is not too long, it was seen to “change into spherical”.
Spikes or radial protrusions are more easily formed. They are cylindrical up to their rounded tip, but always perpendicular to the surface of spheroidal BL like diverging rays ( [33] , p. 114, 116). They can have a length of about 15 cm for instance. Their position changes, but their structure is stable. These observations are strongly in favor of electronic oscillations in a plasma membrane that can even be locally extruded, but only so that oscillations are synchronous. This is also due to a high density of charged particles around the central BL. Rapid diffusion of unbound electrons inside the whole membrane and its extrusions yields everywhere the same density n and the same plasma frequency. The surface charges are thus oscillating in synchrony. Since they have always and everywhere the same sign, they us repel one another. This fact accounts for perpendicular rays, wherever they are attached to the BL. There are also many other and sometimes very puzzling observations that can now be explained. In the future it may be possible to produce authentic BL near installations that produce very high electric tensions and powerful sparks. This could allow for experiments and measurements, but natural BL does already provide many opportunities to test the validity of the proposed explanations.
4. Applications of the Plasma Oscillation Theory
4.1. Spectral Analysis of Emitted Light
Chinese scientists were observing and filming in 2012 ordinary cloud–ground lightning with a high-speed camera and an excellent optical grating. They were fortunate to catch also a BL at a distance of 900 m and the spectrum of its light. They found that the light was not only due to nitrogen and oxygen ions as in the initial lightning, but also from neutral silicon, calcium and iron atoms. This BL had a large diameter (5 m) and appeared immediately after the lightning and close to its impact. It travelled then at 8.6 m/s on a nearly horizontal level. The spectrum indicated that the membrane contained atoms resulting from vaporization of the ground [42] . They were rapidly dispersed in atmospheric air. Probably, the lightning did not only produce a plasma cloud, but also the EM pulse that initiated plasma oscillations. They became then autonomous, but filming at a very high rate revealed even that the intensity of the emitted light varied at the time-scale of milliseconds.
The simplest explanation is that this resulted from plasma oscillations in the kHz region. Since the value of the plasma frequency depends on the density n of unbound electrons in the plasma membrane, the lucky observation becomes even more interesting. A subsequent paper of the same group [43] estimated the maximal luminous intensity of visible light to be 4.2 kW. Usually, the luminosity of BL is comparable to that of an electrical light bulb (50 - 100 W). These authors suggested therefore that this BL could be due to a power-line arc. That is possible and has already been observed. The relevant mechanism and phenomenology merit thus specific investigations.
4.2. Apparently Erratic Motions of BL
BL can enter a house through open doors or windows and move around in a room. After that, it can leave again. An anthropomorphic interpretation of his behavior may suggest that the BL was exploring, but it did only follow a path where it was always attracted by a greater density of charged particles in atmospheric air. In stormy weather, it has to be expected that air is also ionized and more protected in nearly closed rooms. They can there even be created by flames, since they are luminous because of chemical reactions that produce ions. When it was customary to use open fires, the chimneys were attractive places for BL, entering or leaving a house. It did even explode when the density of free electrons and ions was there too high.
Outside houses, BL is usually travelling quite close to the ground, since the ionization density is there optimal. When BL is formed at the level of electrically charged clouds, it darts down to the ground. The atmospheric electric field is progressively increasing and can thus create more charged particles near the surface of the Earth. When BL remains stationary at some places, especially above church towers, this means that the electric field is there higher and can favor ionization. The same phenomenon is well known for pointed conductors in electrostatics. However, BL can also be immobilized when the density of charged particle is identical in all directions.
4.3. Peaceful Extinction or Violent Explosion of BL
It has been reported quite often that a luminous ball did suddenly vanish in air, as if a light bulb had been extinguished. This disappearance results also from plasma oscillations, since they are only sustained by parametric amplification when the surrounding air is sufficiently ionized. I can happen that the inhalation process does not provide enough unbound electrons and ions. It is necessary, indeed, that the density n of unbound electrons in the plasma membrane is high enough to keep the amplitude and frequency of the plasma oscillations at the required level for exciting neutral particles inside the membrane. The frequency of collisions and the velocity of the colliding electrons are essential parameters. When their values are too low, visible BL becomes invisible. It can still survive and become visible again by moving around. Observations could have suggested the existence of invisible BL, but it can only be explained by means of plasma oscillations.
This is also true for explosions of BL. The electron density
could also be adapted by changing the thickness of plasma membranes, but that is a slower process and is limited, even for invisible BL. Their existence explains also why BL can suddenly appear in room. It was already there, but had to become visible. It is not a ghost, but a natural phenomenon that had to be decoded.
4.4. Attraction of BL by Metals and Water
It has been observed that the BL has a special affinity for iron wires in meadows. This results from the fact that the atmospheric electric field is greater in their immediate vicinity. This effect is increased for barbed wires, because of the increased potential gradient near the tip of good conductors. Metallic conducts for draining water from the roof of houses can also attract BL, because of image forces. They result from the fact that any positive point charge that is situated near a metal surface, will attract conduction electrons and produce a negative surface charge. It attracts the external positive charge. When it is negative, it repels conduction electrons, but will then be attracted by the induced positive surface charge. Image force effects explain why cold nuclear fusion is possible [44] , but also very peculiar properties of BL.
We mentioned at the end of Section 2.2 that BL did plunge in water, contained in open reservoirs. It did heat it so much that it boiled and was completely evaporated. These observations raise two problems. 1) Why was BL attracted by liquid water and did even penetrate in this medium? 2) Where did the required energy come from? The answer to the first question results from the fact that liquid water is very polarizable, since water molecules are small and have a practically spherical electron cloud. They can thus easily turn their negative part towards a positive charge, situated above the water level. They would turn their positive part toward an external negative charge. Even when BL remains electrically neutral on the average, its total charge is oscillating because of (9). The polarization of liquid water happens at the plasma frequency. The second question implies a paradox that can be solved, but requires a change of paradigm.
4.5. Normal BL Has No High Energy Content
The word “fire ball” suggested internal heat, but that is not compatible with the fact that when BL was close to witnesses, they felt no increased thermal effects. BL has thus the same temperature than the surrounding air, but inside water, it finds much more charged particles than required for survival. Electrolysis of pure water would be impossible if water molecules did always remain intact. Even at normal temperature, liquid water allows for collisions that produce ions. This yields an equilibrium, since (![]() ). One proton can quite easily pass from one water molecule to another one, when they are in close contact. Of course, OH– ions are not sufficient to sustain plasma oscillations inside the membrane, but the added electron can be detached by colliding electrons.
). One proton can quite easily pass from one water molecule to another one, when they are in close contact. Of course, OH– ions are not sufficient to sustain plasma oscillations inside the membrane, but the added electron can be detached by colliding electrons.
This requires also some energy, of course, but any type of damping can be compensated when parametric amplification is operative. Otherwise, it would be necessary to explain how BL could acquire a huge amount of energy before it plunged in water and in what form it was stored in BL. It is not plausible to assume thermal agitation, since witnesses could detect no heat radiation in atmospheric air. This embarrassing paradox raises a basic problem. It can be solved by parametric amplification, since it implies that more energy can be produced when BL extracts more charged particles from water than from air. Instead of exploding, the BL did heat water, until it was totally evaporated. This proposition can also be tested by examining what happen when BL interacts with metals and glass. These observations are easier to understand when we become aware of another property of BL.
4.6. Radial Plasma Oscillations Require only and Electric Field
Faraday discovered that moving electric charges create a magnetic field and Maxwell found that oscillating charges produce electromagnetic waves. Their existence was unknown, but resulted from combining all know laws and generalizing one of them for logical consistency. Hertz confirmed it for stationary waves generated by means of two parallel wires and then for propagating EM waves created by oscillating electrons inside an electric arc. This was also a plasma, but BL is a very special one, even in regard to Maxwell’s equations. It is true that a constant density n of unbound electrons, displaced by a distance ![]() with respect to their normal position in a plasma membrane, will yield a current density
with respect to their normal position in a plasma membrane, will yield a current density ![]() and an electric field
and an electric field![]() , so that
, so that
![]() and
and ![]()
According to Maxwell’s equation, this should create a magnetic field![]() , since
, since
![]()
However, spherical BL is a special case, since the electric field lines are radial. At a distance r from the center of the sphere, the magnitudes of ![]() and
and ![]() depend in the enclosed charge
depend in the enclosed charge![]() , since
, since
![]() and
and ![]()
Combing the two last relations, we get
![]()
It follows that ![]() inside and outside spherical, spheroidal or cylindrical BL when the current density
inside and outside spherical, spheroidal or cylindrical BL when the current density ![]() and the electric field
and the electric field ![]() are there everywhere transverse to the plasma membrane. It is remarkable that BL would then emit no EM radiation at all. The observed emitted light results only from quantum-mechanical transitions. However, Dimitriev [31] heard that his transistor detected EM noise. It resulted from collisions that deviated electrons from their radial path. Dimitriev heard also some acoustic noise. It was caused by collisions of charged particles with neutral particles and produced sound waves.
are there everywhere transverse to the plasma membrane. It is remarkable that BL would then emit no EM radiation at all. The observed emitted light results only from quantum-mechanical transitions. However, Dimitriev [31] heard that his transistor detected EM noise. It resulted from collisions that deviated electrons from their radial path. Dimitriev heard also some acoustic noise. It was caused by collisions of charged particles with neutral particles and produced sound waves.
4.7. Interaction of BL with Electric Conductors
Fortuitous observations can be very puzzling. It happened for instance that BL was seen to emerge from a socket. Bychkov ( [45] , p. 8) presented 4 drawings of BL that came out a socket. Though it grew in size, it remained connected to both metal wires by means of cylindrical connections. Does this mean that this BL came through the wires or did draw energy from the electrical distribution system? Another example was provided by Seward. He wrote a booklet [46] , where he mentioned an observation of “Ball Lightning forming”. The witness was sitting in a closed room and saw that a small light came out of the receiver of a telephone “like a drop of water”. It blew then up “like a balloon to the size of a soccer ball”. It got detached, bounced upwards and did explode with a very loud bang. It produced even a multitude of pieces, leaving trails in all directions.
Why is it possible that this BL emerged from a telephone receiver? The old telephone set was attached to a wall, but disconnected. Even the handle was hanging downward on its cord. The small initial BL was already luminous, since air was more ionized at the tip of thin wires. This occurred during a nearby thunderstorm that could thus provide a perturbation of a small local plasma cloud. The wires could even act like an antenna, activated by lightning, since it produces EM waves with a broad spectrum of possible frequencies.
It is instructive that the booklet presented a model of BL that was inspired by tokamak systems. This word is the contraction of a Russian expression for a “toroidal chamber with magnetic coils”. Such a machine was constructed in 1968. The objective was to produce energy by nuclear fusion when an adequate and very hot plasma is magnetically confined. Seward thought—with the help of two plasma physicists—that BL could also produce energy by nuclear fusion. Actually, he assumed that inside BL, electrons are spiraling on the surface of a closed cylinder. This would yield a toroid with an internal magnetic field, but no external one. This proposition is speculative, but respectable and shows that the BL phenomenon was a very mysterious.
Another baffling observation was made by a young man, who was fishing at a river [47] . He had attached a worm to the hook and when he felt that a fish had eaten this worm, he wanted to replace it. When the bare hook was raised to about 1 meter above the water, “a shining ball with a diameter of about 5 centimeters suddenly clung to it”. The weather was clear and the fisherman did not see where this luminous ball came from. Being reactive, he lowered the hook and the attached BL in a pail that contained water with already caught fishes. Instead of extinguishing the presumed fire ball, the water began to boil. It produced dense vapor and the fishes were found to be cooked. It was even more astonishing that “the hook tied to the line had disappeared”. This event was used to estimate the energy content of this BL (about 107 J/cm3), but the hypothesis of stored energy is not valid anymore. It is sufficient to accept that the sharply pointed hook favored the formation of a BL. Moreover, it did not only heat the water, but also the metal. The high density of conduction electrons in the metal did tremendously amplify the collective oscillation of electrons inside the plasma membrane of the BL. Instead of exploding, it evaporated the metal.
Another type of interactions of BL with metals is described in the same article. Inside a barn, a BL that was larger than an apple created very notable static electricity. When this ball left, several small pieces of metal and the woman’s metallic rings had disappeared. In another case, a man was knocked down by a BL that had about the size of a tennis ball. When he was found, his golden necklace was evaporated. The burned skin was documented by a photograph ( [46] , p. 7).
Stenhoff reported the remarkable case of a lady, who was surprised in her kitchen by a luminous ball that seemed to hit her below the belt. This happened during a violent thunderstorm, but she had never heard about BL. She did thus “automatically” brush off the intruder, but there appeared redness and swelling on her hand and her gold wedding ring was “burning” into the finger [48] . It is better not to touch BL, which is attracted by metals and does rapidly heat it. This results from the oscillating electric field outside the plasma membrane, since the BL cannot penetrate in the metal, but is able to set conduction electrons in forced oscillation. According to the Drude theory, the absorption would be stronger for oscillation at infrared or lower frequencies. The density of conduction electrons is very high in metals. They are thus vaporized more rapidly than water.
4.8. Surface Tension of BL
The usual spherical form of plasma bubbles requires surface tension, but the cause is not the same as for soap bubbles. In their liquid membranes, molecules that are close to the surface are attracted towards the inside of the liquid. This is not true for plasma membranes, since all free electrons have there the same status. They oscillate like harmonic oscillators. Surface tension of BL is then a volume effect, since the total energy is
![]()
Uo is the internal energy of the same volume of atmospheric air. The added term results from the density n of unbound electrons inside the plasma membrane that are oscillating at the plasma frequency ![]() with an amplitude A. The volume of the membrane is proportional to its external surface S and the small thickness δ of the plasma membrane. Since
with an amplitude A. The volume of the membrane is proportional to its external surface S and the small thickness δ of the plasma membrane. Since ![]() is proportional to the electron density n, the internal energy of BL is proportional to n2. We might add the Coulomb potential energy for all interacting charged particles inside the plasma membrane, but the resulting energy would also be proportional to the surface. BL has thus to be as compact as possible, but fusion of two spherical plasma balls and fragmentation in smaller ones have also been observed.
is proportional to the electron density n, the internal energy of BL is proportional to n2. We might add the Coulomb potential energy for all interacting charged particles inside the plasma membrane, but the resulting energy would also be proportional to the surface. BL has thus to be as compact as possible, but fusion of two spherical plasma balls and fragmentation in smaller ones have also been observed.
Though surface effects modify the energy content of BL, this does not explain the huge energy that is necessary to heat water and even to melt and vaporize metals. This energy was not stored inside BL, but produced by it when the intake of charged particles is much higher than in atmospheric air.
4.9. Passage through Window Panes
This is a particularly astonishing phenomenon, since it can occur in 3 different ways. 1) BL can pass through window glass as if it were not there. Neither the size nor the shape of the plasma ball is modified during the passage and the glass remains perfectly intact. 2) It happens also that there remains a small hole. It is not plausible that it was already there and that BL had the capacity to detect it for getting on the other side. BL has to be able to create such hole. 3) It can even produce a hole that has the same size, as the plasma ball and even the same shape when it is not perfectly round. The cut-out disk is only slightly smaller than the hole and sometimes there are signs of melting. The ring disappeared as if the glass had there been evaporated. These processes are illustrated in Figure 4.
![]()
Figure 4. (a) Passage through a window pane as if it were not there. (b) When the plasma frequency leads to absorption, the glass does melt, especially when the passage is slowed down. (c) Creation of a small hole when the BL is touching the glass. (d) Passage through this hole by deformation of the plasma membrane.
To explain these facts, we note that the dielectric constant and the index of refraction of glass differ from those of air. When BL comes close to a windowpane, it is thus attracted towards the glass by polarizing it. This yields an image force when BL is not electrically neutral. This is true, because of (9). Figure 4(a) represents the passage through window glass, apparently as if there were no obstacle. The plasma membrane is represented in a frequently observed color, but it is divided in two parts, since air cannot penetrate in the glass. However, both parts of the BL are complementary. This results from the global electric field, which is invisible, but radially oscillating at the plasma frequency![]() . This field exceeds the boundaries of the plasma membrane, but it is necessary that
. This field exceeds the boundaries of the plasma membrane, but it is necessary that ![]() is situated in the frequency domain where glass is transparent. The value of
is situated in the frequency domain where glass is transparent. The value of ![]() depends on the density n of unbound electrons because of (1), but this value is unknown. It can thus happen that the oscillating electric field is not absorbed by glass. A transistor radio, for instance, is able to receive EM trough glass.
depends on the density n of unbound electrons because of (1), but this value is unknown. It can thus happen that the oscillating electric field is not absorbed by glass. A transistor radio, for instance, is able to receive EM trough glass.
Figure 4(b) shows what can happen when the plasma frequency is situated in a domain, where normal glass is absorbing. Because of exponentially increasing parametric amplification, the heating can get so strong that the glass melts and is even vaporized. This effect is maximal when the oscillating electric field is parallel to the glass plate. The BL is then slowed down, since it is equally attracted to both sides of the window glass. Figure 4(c) applies to the case where it is sufficient that the BL touches the glass, to heat it locally so much that it creates a hole. It is small, but the plasma membrane can pass through it, as shown in Figure 4(d). The mystery of the passage of BL through glass can thus be elucidated in a logically coherent way.
It is now more interesting to return to witness accounts and other attempts to understand what happened. We mentioned already the enormous data collection, realized by Grigorjev et al. [26] . Among 5315 cases of BL observations, collected in Russia, 43 cases were selected to illustrate “penetration into closed rooms” through glass or by coming out of sockets of various types [21] . It could only be concluded that “BL may simultaneously possess two exotic properties” in closed rooms. The passage of BL through window panes by leaving circular holes was observed in 26 cases. Rings were cut out, but the cause of assumed “thermal stress” remained mysterious.
The extension of the puzzle can be illustrated by a proposition of two scientists, who claimed that BL is merely “self-confined light” [49] . They assumed that air can be strongly compressed in a thin layer and constitute a “spherical space soliton”. Actually, they thought that in atmospheric air, the shell would be a wave guide for light and could penetrate in glass and come out on the other side by refraction. Why could air be able to pass through the glass, even if it were compressed? The study of Bychkov, Nikitin et al. [50] was very different. It was based on extensive knowledge of BL phenomena. These authors insisted thus on the existence of 3 types of possible interactions of BL with glass and analyzed these observations in terms of two often mentioned theoretical concepts. 1) BL could be an “electrical discharge”, sustained by some external energy source. 2) It may be a “material object” with a huge amount of internal energy.
Nikitin tried to justify the second model, by proposing that BL is constituted of a “core” that contains an excess of positively charged particles, surrounded by a spherical shell of polarized dielectric material. This structure should make it (somehow) possible to store enormous internal energy, to account for the capacity to heat, melt and vaporize metals and glass. That glass is able to absorb energy was demonstrated by an experimental investigation. The transmittance of laser light through a glass pane that had been heated by a BL led to the discovery of “spherical inclusions”. Their size was about 1 micron. We confirm that small metal particles would absorb energy, since the oscillating electric field would set the conduction electrons in forced oscillations and heat the metal [37] . Even small spherical voids in a polarizable medium, subjected to an oscillating electric field, would create dipolar surface charges and absorption. We should thus consider the possibility that the plasma frequency is situated in a domain where glass is absorbing EM waves without inclusions. The authors of the best study concerning the passage of BL through glass [49] recognized their perplexity, because of observations where BL is cool and other ones, where it seems to be very hot.
5. Conclusions
The reality of the BL phenomenon cannot be doubted anymore, but is very complex. Though it is a natural phenomenon, it can be compared to another type of aerial phenomena. They are even called “Unidentified Aerial Phenomena” (UPA) to hide the embarrassment caused by “Unconventional Flying Objects” (UFOs). In both cases, “skeptics” believe that what cannot be explained by known theories has to result from illusions. On the contrary, problems that are difficult to solve can be of fundamental importance in science. Its actual duty is then to investigate then even more and to explain the mysteries instead of pretending that there is no problem. That is the usual way to progress in science and deserves to be attentive to anomalies and strange facts.
Sometimes, the confusion results from hyper-specialization and lack of interdisciplinary dialogue. The concept of plasma oscillations, for instance, was already known more than half a century ago in solid-state physics. It was ignored or believed to be irrelevant for atmospheric electricity. Incidentally, we did explain “anomalous optical properties” of small metal particles by means of collective oscillation of conduction electrons. When we became aware of the enigmatic BL phenomenon, we wondered if the luminosity of BL could be due to a thin membrane, containing unbound electrons and ions. We proposed the theory of plasma oscillation and parametric amplification in 2010 at an Internal Symposium on Ball Lightning (ISBL). Since the article was published [40] without any impact, we try again. We have also to insist on the fact that plasma oscillations lead to absorption in metal particles, but not in BL when it is freely moving in atmospheric air. Plasma oscillations are there even sustained.
It is always necessary to know as much as possible about relevant observations, before any attempt to understand what happened (chapter 1 and 2). The basic purpose of the theory of plasma oscillations for BL was to explain that constant losses of energy and charged particles can be compensated (chapter 3). A corollary was that “invisible BL” is also possible and can survive. Many applications of this theory are even possible and useful (chapter 4). They explain BL phenomena, in spite of their variety and paradoxical aspects. It should also be noted that we are accustomed to focalize attention on the behavior of single particles or constituting elements. However, we should not forget that cooperation is also possible. Even scientific research is a matter of collaboration and requires easy access to information.