
1. Introduction
In 1912 V. I. Vernadsky at the meeting of the Russian Imperial Academy of Sciences gave the report: “About studying of gas breath of Earth”. He suggested that from the Earth interior there has to be the flow of different gases and called this phenomenon “Gas breath of Earth”. Afterwards, this assumption was confirmed in field observations. Later change of the flow of radon by preparation of tectonic earthquakes was revealed (for example, [1] ). This phenomenon received the name of the radon precursor of the tectonic earthquake. The mechanism of this precursor is almost obvious: by preparation of the tectonic earthquake there is the deformation of the porous and cracked environment (crust) which changes effective coefficient of the mass transfer.
Volume deformation has basic meaning and its distribution defines distribution of the fluid precursor. Short-term precursors because on big intervals of time there is the alignment of the flow are of special interest. It is also necessary to remember that time of half-decay of radon is about 4 days.
In this work calculation of the short-term fluid precursor for this mechanism will be made.
2. Main Notations
x, y, z is Cartesian coordinate system from the beginning in heterogeneity epicenter, [m];
t is time from the beginning of action of the short-term precursor, [s];
s is tangential stress at infinity (boundary condition), [Pa] = [kg/(m⋅s2)];
G is shear modulus of the Earth’s crust, [Pa];
α is relative increment in shear modulus in heterogeneity;
ε is the volume strain of the environment;
h is depth of hypocenter of the spherical heterogeneity, [m];
R is radius of the spherical heterogeneity, [m];
P(x, y, z, t) is the abundant porous pressure;
μ is coefficient of dynamical viscosity of fluid, [Pa⋅s];
k is permeability, [m2];
m and m0 are the current and initial porosity of the medium;
V is velocity of fluid, [m/s];
U is velocity of solid phase, [m/s];
W is velocity of Darcy, [m/s];
β is isothermal compressibility of fluid, [1/Pa];
H is Heaviside function;
δ is delta-function;
Δ is Laplace operator with respect to spatial variables.
3. Equations of the Two-Phase Medium
In the linear approximation, in the case of slow processes, when inertial forces and compressibility of the solid phase can be neglected with respect to the compressibility of fluid, the system of equations of dynamics of a porous fluid has the form
(3.1)
(3.2)
Equation (3.1) is, in essence, Darcy’s law, Equation (3.2) describes deformation of the fluid in the elementary volume of the two-phase environment.
After the transformations which are in detail stated in [2] the equation turns out
(3.3)
In stationary mode from (3.3) we have
(3.4)
At
(3.3) and (3.4) give respectively the equations
(3.5)
(3.6)
4. Background Flow of Fluids
Let’s consider the background flow homogeneous and stationary. It is described by Equation (3.6) with boundary condition of free outpouring on the surface
(4.1)
During the aseismatic period the flow is observed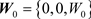 , and according to Darcy’s law is expressed as
, and according to Darcy’s law is expressed as
(4.2)
Therefore, the solution of the system (4.1) is
(4.3)
5. Deformation of the Environment by Preparation of the Tectonic Earthquake
From positions of mechanics of continuous medium process of preparation of the tectonic earthquake is considered as process of forming in the environment of heterogeneity of properties [3] . Two periods are allocated: long-term and short-term precursors. At the stage of long-term precursors heterogeneity arises and develops; in the period of short-term precursor it begins to collapse. At the beginning of action of short-term precursor for spherical heterogeneity at Poisson’s coefficient ν = 1/4 volume deformation has the appearance [3]
(5.1)
where
,
,
is radius of spherical heterogeneity, M is magnitude of future earthquake.
Let’s consider the short-term precursor. Let’s assume that at the beginning of action of the short-term precursor the cumulative deformation is dumped to zero and further remains invariable
(5.2)
Of course, also other law of behavior of deformation during action of the short-term precursor is possible.
6. The Flow Perturbed with the Earthquake Precursor
In Equation (3.5) we will denote
(6.1)
Derivative from (5.2)
(6.2)
Now the system from Equation (3.5) with boundary and initial conditions registers as
(6.3)
The solution of system (6.3) is given by formula (A.2).
Important note. Thanks to the Heaviside function (5.1) suffers the gap, and at integration it leads to significant increase in time of calculations. However, such situation can be improved if to accept approximate representation
(6.4)
At n = 20 - 30 the error from such replacement becomes quite acceptable.
7. Merely Precursor Perturbation
To allocate such perturbation, we believe in (6.3)
and we receive the system for M
(7.1)
Then
(7.2)
In this solution dominant function is
(7.3)
and
(7.4)
where
,
.
Practical interest represents the fluid flow on z = 0 surface. This flow is defined by Darcy’s formula and has the appearance
(7.5)
Statement and the solution of problem (7.1)-(7.5) can be executed in dimensionless quantities. We postulate
(7.6)
When transforming delta-function it is necessary to use the ratio
(7.7)
Then (7.1) takes the form
(7.8)
In the dimensionless form (7.2) is
(7.9)
where
,
,
,
,
.
Based on formula (7.5), the dimensionless speed of Darcy on the surface has the appearance
(7.10)
Here
(7.11)
In Figures 1-3 lines of equal level are given in the first quadrant. On the neighboring quadrants continuation is made is antisymmetric, and, therefore, areas of decrease and increase of effect alternate. Such situation will be coordinated with empirical data.
![]()
Figure 1. The plot of function
при
,
in the first quadrant. Axes of coordinates are zero lines.
![]()
Figure 2. The plot of function
при
,
in the first quadrant. Axes of coordinates are zero lines.
![]()
Figure 3. The plot of function
при
,
in the first quadrant. Axes of coordinates are zero lines.
8. Conclusion
In formula (7.11) the radius R is in the denominator. Therefore, at increase in magnitude of future earthquake the precursor effect with other equal conditions will be less. Empirically it is almost impossible to check this conclusion as it is difficult to meet “other equal conditions”. On the other hand, this conclusion is not unexpected. For the earthquake of bigger magnitude, the same deformation extends to the big area and becomes more flat.
The main conclusion can be formulated so: the chosen technique can be applied to calculations of fluid precursors of the tectonic earthquake.
Appendix: Parabolic Equation
The first boundary value problem for the parabolic equation with constant coefficients and its solution for half-spaces are defined by the following formulas
(A.1)
and the solution is expressed by means of dominant function
(A.2)
where S and V are the surface and volume of the half-space respectively, integration on time is made in the form of convolution.
Dominant function for half-spaces
(A.3)
In the analysis of this solution, it is useful to mean ratio
(A.4)
These data can be found in any, rather full textbook on the equations of mathematical physics or in the reference book on mathematics.