The Perihelion Precession of the Planets Indicates a Variability of the Gravitational Constant ()
1. The Gravitational Constant G
Newton’s law of forces from 1686 has a weakness that causes the results of gravitational force calculations to be inaccurate [1] . Although the law takes into account the quadratic dilution of the lines of force in the case of a spherical propagation in space, it neglects the fact that the lines of force of the gravitational force field diminish potentially with increasing distance, so that gravitation is not only diluting according to its spatial extension, furthermore, additionally weakens accordingly to a potentially decreasing curve.
2. Observable Effects of Gravitation
At very large distances, the observable effects of gravity indicate a reduction of the gravitational attraction, whereas the gravitational attraction is larger at very small distances (e.g. in the atomic regime). This behavior of gravity is best represented by a power function. A similar perception of a modified gravity is published by [2] Nojiri, S. and Odintsov, S. (2007) as well as by [3] Hees et al. (2014). Another attempt to improve the concept of a gravitational constant or even eliminate the gravitational constant was undertaken by [4] E. G. Haug. He published several articles about this subject (papers of 2016 [4] , 2018 [5] , 2022 [6] ). In his paper 2022 E. G. Haug proposes to eliminate the gravitational constant competely from the gravitations formula as Newton did not use it in his gravitations formula of 1686. He also attempted to improve the calculation of the perihelion precession of the planet Mercury (2020), however, he does not pursue his formula predictions of the perihelion precession of the other planets. This, however, is the main theme of this article of H. P. Weber.
There are a number of anomalies of gravity. The most spectacular is the perihelion precession of the planets. If Newton’s law from 1686 were correct, the planetary orbits would describe an exact ellipse. However, this is not correct. The measured deviations, the perihelion precessions, are very small, but significant. The deviations sum up after hundred years to some extent, so reliable results of the observations are obtained. Most obvious are those with the planet Mercury near the sun with 43.11 arcsec per century.
Albert Einstein knew this problem with the gravitation since he dealt with it in the General Relativity Theory (GRT), which he developed mainly by including the gravitation. To solve the problem Einstein adapted the formulas of the GRT (i.e. the gravitation constant) to the orders of magnitude of the specific situation in our solar system accordingly, and could achieve thereby quite exact matching results with the measured values. He considered this also as a proof of the correctness of the GRT.
However, the GRT does not deliver useful results in every case. Some unresolved cases remain for the distance “r”, for which the theory of relativity does not give results, or is invalid.
These are the cases below the Planck horizon and above the size of the solar system. Thus, for example, it was not possible so far to bring about the unification of the nuclear forces with gravitation.
In contrast to Einstein, this new approach tries to develop the gravitational formula with the help of a power function in such a way that the gravitation just shows the deviations which explain the observed perihelion precession of the planets. EINSTEINs formula
is not disregarded, but the formula is enhanced with a variable which can now be applied to a wider range of cases for the gravitation.
The masses do not play any role, but gravitation depends on “r” itself. Thus the law of Newton has been modified in a manner that relativistic corrections are not necessary any more.
3. Mathematical Approach
The conventional formula of NEWTON is giving the gravitational force “F” as follows:
(1)
The gravitational constant is modified in this article as follows
(2)
It can also be written as:
Here, the constant k1 is the conventional gravitational constant adjusted about one meter (Correction = 1.00002419). This is a parallel shift to keep the perihelion precession centered.
The constant k2 contains the Rydberg constant R, which adjusts the curve of Formula (4) (Figure 1) to better line-up the planets. The constants k1 and k2 were aligned to the perihelion shift of the planets.
![]()
Figure 1. The perihelion precession of the planets.
4. The Perihelion Precessions of the Planetary Orbits
According to Newton, the orbit of the planets should describe exactly one ellipse in the course of one full rotation. In reality, however, the perihelion, the point of the ellipse facing away from the sun, shifts a small amount each year, so that the orbit becomes a rosette. In Table 1 three different values of the perihelion precession of the planets are listed as measured in angular seconds (arcsec) per century. In Column 1 values from the literature are given as comparison to the calculated values with conventional method approach using Einstein gravitational constant listed in Column 2 and with the new Gvar given in Column 3.
4.1. Table 1, Column 1
The values in the Column 1 were taken from the literature. No values could be found for the planets outside the orbit of Mars, except data from Saturn with a perihelion precession of −0.006arcsec derived from the Cassini project of NASA. However, there are still unresolved uncertaincies of the interpretation of the measurements of the Saturn perihelion precession.
4.2. Table 1, Column 2
The values of the perihelion precession (PP) in Column 2 were calculated relativistically with Formula (3) using
according to EINSTEIN. The “anomalous” percession of Jupiter and Saturn was investigated among others by [7] Pitjeva and Pitjev (2006) and [8] Iorio, L. (2009). Iorio’s explanation failed as he tried to place a large mass in the outer solar system, which probably does not exist.
![]()
Table 1. Perihelion precessions of the planets.
(3)
G = gravitational constant (conventional), M = mass of the sun,
msa = major semi-axis of planet orbit, a = number of orbits per year,
e = Eccentricity, c = speed of light.
4.3. Table 1, Column 3
The values of the perihelion precession (PP) in Column 3 are calculated by the rotational velocity of the planets (v) with Formula (4) using once  according to EINSTEIN and once with
according to EINSTEIN and once with  of Formula (2) considering the eccentricity of the planetary orbits (arcsec per century).
of Formula (2) considering the eccentricity of the planetary orbits (arcsec per century).
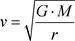 (4)
(4)
5. Results and Conclusion
Comparing the two calculated perihelion deviations of Table 1, columns 2 and 3, we find that the planets Mercury to Mars show positive perihelion precessions with both types of calculations. However, the outer planets from Ceres to Pluto show only positive values with the Einstein formula. Calculated with Gvar, the values of these planets in the red curve become negative!
6. Outlook
The “anomalous” precession values of the outer planets found by the Cassini probe are no anomalies but in fact conform with a variable gravitational Gvar, and it is a necessity and quite reasonable to consider the gravitational constant as a variable. Thus, the law of Newton is modified in a manner that relativistic corrections are not necessary any more. The whole cosmos becomes mathematically analytically accessible with this approach. In [9] Weber, H. P. (2019) and in future publications different phenomena of the gravitation are calculated with the variable Gvar. Emphasis will be given to the effects of the flexible G on the Planck units and the equivalence relations calculated on their basis. The author hopes having contributed to a better understandig of gravitational forces and is looking forward to a fruitful discussion on this new approach.