1. Introduction
The high-entropy alloys (HEA) have attracted considerable attention in recent years [1] [2] . These alloys consist of several principal elements that are stabilized due to high configurational entropy. The atoms in HEA are randomly distributed on ordered lattice as has been inferred from the sharp X-ray diffraction peaks. Distortion of the lattice of the order of 1 percent has also been concluded from theoretical calculations [3] . These alloys show better mechanical properties and superparamagnetism. Recently, superconductivity has been observed in transition metal based HEA (Nb0.33Ta0.34)1−X(Hf0.08Zr0.14Ti0.11)X, which has bcc lattice structure [4] [5] [6] [7] . (Hereafter, we replace (Nb0.33Ta0.34)1−X(Hf0.08Zr0.14Ti0.11)X by (NbTa)1−X(HfZrTi)X, for simplicity.) The superconducting transition temperature (TC) has been found to vary from 7.9 K to 4.6 K as the atomic fraction x increases from 0.2 to 0.84. The elements Nb, Ta, Hf, Zr and Ti have TC s; 9.5 K, 4.5 K, 0.1 K, 0.5 K and 0.4 K, respectively, which ranges from 0.1 K to 9.5 K [8] . One important observation is the “cocktail-effect” which refers to the enhancement of TC beyond the simple mixture of those of constituent elements [7] . The occurrence of superconductivity is often considered empirically using the variation of TC as a function of number of outer electrons/atom (e/a) [5] (aka Matthias rule). The variation of TC with e/a in this HEA falls between that of crystalline and amorphous transition metals and alloys. A maximum of TC occurs for e/a = 4.7 which is within the range of values of e/a (4.3 to 5.0) for the crystalline system. In this paper, the superconductivity in (NbTa)1−X(HfZrTi)X HEA is explained using the theory of strong-coupled superconductors [9] .
2. Superconductivity in (NbTa)1−X(HfZrTi)X HEA
The effect of disorder on superconductivity has been studied before, for example, the universal degradation of TC in A15 compounds ( [10] and the references in [10] ). Here, the effect of disorder in (NbTa)1−X(HfZrTi)X HEA is explained in terms of localization of electronic states [11] . The randomness of transition metal atoms in the lattice positions of (NbTa)1−X(HfZrTi)X is expected to affect the electronic band structure. In this regard, localization of electronic states can occur when the electronic band width (U) is comparable to the distribution width (W) of the site energy. The site energy can be taken to be the first ionization energy of the constituent atoms. The first ionization energies of Nb, Ta, Hf, Zr and Ti are 6.77 eV, 7.88 eV, 7 eV, 6.95 eV and 6.83 eV, respectively, which ranges from 6.77 eV to 7.88 eV [8] and therefore, W in this alloy is of the order of eV. Since the typical width of d-band is of the order of eV [12] , one expects localization of electronic states, as U~W. Next, one can examine what can be concluded from the Ioffe-Regel criterion, which states that electronic states can be localized for kl < 1 and are extended, otherwise [13] . Here, k and l are wave vector and mean-free path, respectively, of the electron in the solid. The mean-free path in this HEA is of the order of 10−7 cm [6] and from the Ioffe-Regel criterion one obtains k < 107 cm−1, which is fairly low compared to the typical value of kF in metals (~108 cm−1) [8] . Localization can give rise to mobility edges of electronic band. In addition, disorder can also broaden the width of the d-band density of states.
Approximate solutions of the Gor’kov-Eliashberg form of the theory of strong-coupled superconductors has been of interest for a long time [9] . First, the TC of (NbTa)1−X(HfZrTi)X HEA, is examined with some redundancy in the weak coupling limit [14] . Table 1 gives various parameters relevant for the superconductivity in this HEA. The Debye temperature (ΘD) in Table 1 for x = 0.3 is from [5] . For other compositions of this HEA in Table 1, ΘD is calculated from the well known proportionality:
, where M is the molecular weight. TC s of the HEA in Table 1 are obtained from Figure 3 of [5] . In the weak-coupling limit TC is given as follows [14] :
(1)
![]()
Table 1. Measured and calculated values of TC, M, ΘD and N(0)V for (Nb0.33Ta0.34)1−X(Hf0.08Zr0.14Ti0.11)X HEA.
where, N(0)V is a dimensionless electron-phonon coupling constant. It is noted that in the weak-coupling limit the frequency dependence of the interaction is ignored. The calculated values of N(0)V using Equation (1) are given in Table 1, which are nearly 0.3. N(0)V is found to increase with x until x = 0.3 and then decreases with further increase in x. The decrease of N(0)V with increase of x can be attributed primarily due to the reduction of N(0).
The theory of strong-coupled superconductors includes frequency dependences of phonon-induced interaction and instantaneous Coulomb repulsion. In order to understand the influence of Coulomb interaction on the phonon induced interaction, the strong-coupling case is considered. In the strong-coupling case, TC is obtained as a function of electron-phonon and electron-electron coupling constants, which is given by (aka McMillan equation) [15] :
(2)
where λ is the electron-phonon coupling constant and μ* is the Coulomb pseudopotential. The Coulomb pseudopotential is given by [14] :
(3)
where EB and ω0 are cutoffs of instantaneous Coulomb repulsion and phonon induced interactions, respectively. Since ΘD is known (Table 1) and there are two unknown parameters in the exponential of Equation (2), λ is taken from the weak-coupling limit. Using Equation (2) and Equation (3) and taking ω0 as that corresponding to the Debye temperature, the e/a dependence of EB is obtained, which is shown in Figure 1.
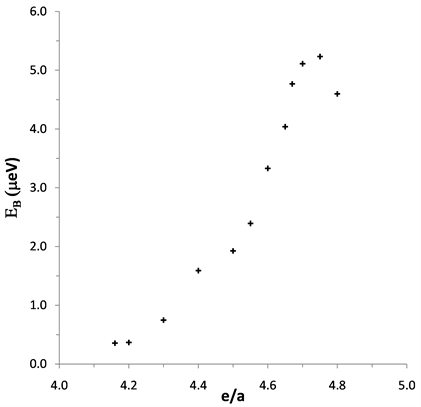
Figure-1. EB as a function of (e/a) in superconducting (Nb0.33Ta0.34)1−X(Hf0.08Zr0.14Ti0.11)X HEA. e/a decreases from 4.8 to 4.16 as x increases from 0.2 to 0.84.
3. Discussion and Conclusions
It is seen that EB is of the order of μeV, which is considerably smaller than ω0. The small value of EB can be attributed to the formation of mobility edge. The peak in Figure 1 can be due to initial broadening of the electronic band and with the increase of x beyond 0.3, EB reduces due to localization of electronic states. The nearly temperature independent high resistivity (~50 μΩ·cm) which is nearly 0.2 times the resistivity saturation value (~ 250 μΩ·cm) [16] also supports this conclusion. This occurs since the energy range for scattering is limited by EB rather than kT. Enhancement of TC is also expected in the approximate solution to the theory when EB
ω0, which accounts for the cocktail effect in this HEA [7] . Superconductivity has been studied in (NbTaTiZr)-based HEA with the addition of Hf, Fe, Ge, Si and V [6] . The ionization energies of Hf, Fe, Ge, Si and V are comparable to that of Nb, Ta, Ti and Zr. The ionization energy of La is 5.61 eV, which is considerably smaller than Nb (6.77 eV). It is therefore, suggested that metal to insulator transition can occur in (NbTa)1−X(HfZrTi)X HEA by the replacement of Hf with La, which increases the distribution width W.
In conclusion, the experimental results on superconductivity in (NbTa)1−X(HfZrTi)X have been analyzed using the Gor’kov-Eliashberg form of the theory for strong-coupled superconductors. The variation in the superconducting transition temperature from 7.9 K to 4.6 K as x increases from 0.2 to 0.84 is explained in terms of decrease in electronic band width due to localization and broadening of the band. The formation of the mobility edge is found to reduce the effective band width in these alloys. The cocktail effect in this HEA is explained in terms of the enhancement of TC, when EB
ω0.
Acknowledgements
The author is benefited from his visit to Europe in 1988-92 for HTSC research; Xiamen, China, during 1995 for STATPHYS19 conference and New Orleans and Dallas, USA during 2008 and 2011, respectively, for APS March meeting. The author thanks the referee for several helpful suggestions. The author thanks Joseph for constant encouragement.