A DX-Like Ternary/Pair-Map, Its Eco-Entropy Scheme, and Managerial Diversity of Nature versus Artifacts Type on Sandwich Theory ()
1. Introduction
Since the 1970’s, there have been many scientific principles and discussions on the method, time, and manufacturing management of the art (academic enterprise, physics, economics, etc.) of 3M & I, in which 3M represents human, Material and Money, and I represent information (Matsui, 2008; Matsui, 2014a) . These are already considered as a class of artifacts science since Taylor (Taylor, 1947) , whereas the nature versus artifacts’ body is recently outlined as a hyperboloid (Matsui, 2022a; Matsui, 2023) , and the managerial body is currently being discussed to address certain realization problems (Matsui, 2016; Matsui, 2019) .
The problem means to pursue the sustainable eco-entropy as redundancy (constraints) in cybernetics (Wiener, 1961; Ashby, 1956) , or marginal profit, value, and diversity in economics (Matsui, 2008; Ashby, 1960) . Therefore, this paper will discuss the following problem of realizing the DX-like microcosm of the ternary/pair-map with allowance (buffer), its eco-entropy scheme, and managerial diversity of nature versus artifacts’ body, on the sandwich theory. At the next following sections, the realization and managerial body would be prepared towards the final geometric realization of body at 3D type.
For the individual (body), the artifacts science proposes and advances with a new academic discipline of individual theory, comprising of the 5-principle with 3-rule (pair-body, dualism, and marginal diversity) (Matsui, 2020; Matsui, 2016) . The fundamental units of individual science are the quanta and cells of the nanoworld corresponding to 3M & I in artificial bodies (Matsui, 2008; Ashby, 1960) . These three have a common mechanism of clock system (compared to dualism), and their integrated system is the fractal total exhibiting a single lobe (elliptical) hyperboloid.
Quantum comprises the duality of grain and wave, with the wave nature being similar to that of a clock. In addition, cells have a circadian clock and operate in a clock system. In the 3M & I of artificial bodies, the clockwork mechanism can be seen in the 24 hours convenience store system (Matsui, 2019, 2023) . These dynamisms reflect in the discreet progressive control approach. The shape of nature versus artifact bodies (or artificial society) is being questioned further, through their exposure to the nano-like world, coronavirus, quantum, and cell. Among them, the microcosm of artifact bodies is a miniature containing the prevalent 3M & I: human, material, machine, and information, where this miniature (from 3D to 2D) is considered to fall within the pair map category that originated in 1983 (Matsui, 2019) .
The pair map format (compass) and artificial Sollen are obtained not only for demand-to-supply enterprises (Matsui, 2008) , but also for physical, biological, and economic entities in the natural world, with the expectation of future verification and demonstration to artificial design. The condensed structure or clock model obtained from the depth of individual science is mathematically clarified (Matsui’s theory), along with the embedded dynamism (fractal and wave equation). In addition, the center of the pair map hyperplane (Nash’s zone) corresponds to the artifact body’s collapse, thus seemingly corresponding to the black hole in space, corporate bankruptcies in the market-economy, and the Three Cs in the corona-stricken society (Matsui, 2019, 2020) .
This becomes the core of subsequent research as the matrix of Matsui’s equation type (Ashby, 1956) , making it possible to draw a miniature of an artificial body and obtain an outlook of the microcosm. Can individual science embody the ideal situation in the post-corona world? In future, the universe will consist of the two-body, three-body (Matsui, 2008; Matsui, 2014a) , or SDGs-body problems. These include the numerical collaboration of automatic driving (Matsui, 2022b) , the fairness of trickle-down economics (Matsui, 2022a) , the Shukyaku-gouitsu (ternary body) in Nishida philosophy (Nishida, 1911) , and the modern SDGs-class body.
Especially for a 3-body-type class, the theory of pair-body would prove to be interesting and would be characterized as the ternary SW, which is a special class of pair-map (Matsui, 2023) .
2. Outline of Realization and Managerial Body
2.1. Pair-Hierarchy, Ternary Body, and Eco-Entropy Scheme
The prevalent artifacts science shows the pair-hierarchy of nature versus artifacts body in Matsui (2020) . Based on this scheme, the sandwich case of enterprise body is characterized with the central dualism of lower and upper levels, as is portrayed in Figure 1. The ternary SW of enterprise body depicts the managerial type that includes the (revenue = cost + profit) equation in nature versus artifacts class. For the ternary SW, the similar constraints and eco-entropy problem are seen in the case of demand = supply (without buffer).
This problem brings forth the DX-like transformation of pair-map at SW dualism, with the help of Matsui’s ME and graph approach. Further, Figure 1 portrays the X-shape of pair-map. Therefore, the better realization indicates that the persuasion of such a sustainable eco-entropy is a Chameleon’s criteria, which
![]()
Figure 1. Pair-body management of loop conveyor and ternary SW type at pair-hierarchy. At SW
“DX”, the management pursues Cost + Profit → Revenue.
could have originated from the class of eigenvalue or progressive problem. Contradictorily, the prevalent pair-map is usable for the case of demand versus supply (with buffer), and would be later seen as a relaxation problem of eigenvalue or progressive equation type.
2.2. Typical Cases of Ternary SW/Pair-Map
Similar to Figure 1, Table 1 shows the other typical cases of ternary SW on eco-entropy. These are also the formulation styles for nature versus artifacts’ body at sustainability, and this originates in the dualism of cost/motion (FE/T) versus profit/power (EN/V) on sandwich theory, or Matsui’s/Newton’s law (Matsui, 2016) .
Also, it is noted that this ternary SW has been already pointed out in the case of physics (Matsui, 2023) .
3. Ternary Realization Problem of Enterprise Case
3.1. Enterprise Case of Ternary SW
Continuing from Figure 1, the enterprise case of ternary SW is also seen at Figure 2, which shows the outline of ternary SW at profit equation, and is corresponded to the ternary SW of enterprise. Figure 2(a) is the lower level of ternary SW, and Figure 2(b) is the upper level of ternary SW. At Figure 2(b), EN → EC follows a longer entropy, contradictory to the alternate way of eco-entropy.
In Figure 2, the positioning of marginal inventory, SW, would usually not be internal, but the pair-map outside the internal of triangle at Figure 2, and also, the eco-entropy, MP, would usually keep in triangle. Specially, it is noted that ER’ > MP > ER at pair-map. That is,
(1)
where fixed cost (fix C) > variable cost (EC).
![]()
Table 1. Typical cases of ternary SW at pair-map by the dualism (of EC versus EN).
![]() (a)
(a) ![]() (b)
(b)
Figure 2. Ternary SW: Type of enterprise body (ER < fix C + EN, if fix C > EC). (a) Lower level “processing”; (b) Upper level (fix C > EC) “economics”.
Further, from Figure 2, the synthesis of lower (a) and upper (b) could be imaged as a sandwich-like type (Matsui, 2022b) at pair-map.
3.2. Realization Problem and Eigenvalue
Matsui’s ME (Matsui, 2016, 2019) can provide a formulation problem of pair-map, based on our artifact science. Subsequently, the type of ternary SW becomes the prevalently known eigenvalue problem, and is also considered as the Matsui’s ME of type II. Its simple form is as follows:
, if demand = supply. (2)
Therefore, this ternary equation can be generalized as any other relaxation problem under demand ≠ supply (Matsui, 2014b) , and also as a type of progressive equation (Matsui, 2013; Aiyoshi & Shimizu, 1981) as follows:
ketsu > Conclusion sho > Development ki > Introduction
EC (next-order) + EN (end-inventory) = ER (next-demand)
ten > Transformation
+ MI (basic-inventory) (3)
where Chinese story is known as ki-sho-ten-ketsu logics, that notes the equality between the left hand and the right hand.
4. Information and Energy Cases
4.1. Information Case of Ternary SW
This ternary SW is seen in Figure 4. Figure 4(a) is the lower case of ternary SW, and Figure 4(b) is the upper case of ternary SW in information type. From Table 1, Figure 3 would be similar to Figure 2.
4.2. Energy Case of Ternary SW
The ternary SW of energy (heat) type is seen at Figure 5. Figure 5(a) is the lower case of ternary SW, and Figure 5(b) is the upper case of ternary SW in energy type. From Table 1, Figure 4 would be similar to Figure 2.
5. Further Consideration on Ternary SW/Pair-Map
5.1. A Geometric View of Ternary SW/Pair-Map
A Geometric approach to ternary SW/pair-map is here possible and could be outlined at Figure 5 as 3D-type. This identification of 3D-type would show the systematic unification of ternary SW/pair-map, and might be able to utilize a managerial and sustainable approach to the object of bodies by projective geometry.
![]() (a)
(a)![]() (b)
(b)
Figure 3. Ternary SW: Type of information body. (a) Lower level of information body “processing”; (b) Upper level of information body “economics”.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Ternary SW: Type of heat body. (a) Lower level of heat body “processing”; (b) Upper level of heat body “economics”.
![]()
Figure 5. An Outline of ternary SW/pair-map at 3D (p: price, α1 = busy cost and ρ = m/d).
5.2. An Additional Consideration on Eco-Entropy
The concept of eco-entropy is earlier introduced at ternary SW. This is the case of demand (speed), d = m, without buffer. Hence, the ratio of EC and EN can be EN = 0.83 through the following two ways.
1) Type of demand = supply (speed)
A physical system of loop conveyor type is partly prepared from Matsui (2022a) . Now, let us introduce Figure 6, where the triangle ∆αβγ and ∆αβM are similar to each other. Thus, from
and
![]()
Figure 6. An indication of marginal-profit or diversity (eco-entropy).
(4)
the following relations are obtained considering ER = 1, as follows: EC = ER × EN or EN = 0.38 and EC = 0.62. Similar to Equation (2), this result would be similar to the efficiency of 0.62 versus muda 0.38, where the value 0.38 could be regarded as eco-entropy.
2) Type of demand versus supply
The type of demand versus supply (speed) could be generally followed by the progressive equation (Matsui, 2014b; Matsui, 2013) . Let us consider that the notations of O, I, D and MI are represented by the next-order, end-inventory, next-demand, and marginal inventory (profit), respectively. Then,
(5)
Especially for the case of d = m and MI(0), Matsui’s matrix equation (Matsui’s ME) would be available, and its corresponding equation is seen as follows
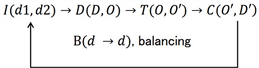 (6)
(6)
where the type of d = m is
and
. (7)
Therefore, Matsui’s ME of type II is given to eigenvalue by the matrix notation:
by Ashby (1956) , and the adjustment of eco-entropy could be attained by T-transformation of DX-type.
6. Conclusion and Nano-DX Remark
This paper will discuss the following problem of realizing the DX-like microcosm of ternary/pair-map, its eco-entropy scheme, and managerial diversity of nature versus artifacts’ body, on the sandwich theory. First, an outline of ternary SW (sandwich)/pair-map is geometrically prepared, along with the introduction and discussion of eco-entropy concept based on the three types of energy, economy, and information body without buffer. Subsequently, a managerial problem of body’s diversity is proposed and formulated at topics of the spectrum of 3M & I-world.
Next, the relaxation problem of ternary SW/pair-map with allowance (buffer/delay) will be remarked as the case of demand-equals-supply (without buffer), and re-named as an allowed buffer type of ternary SW, or a 2-center case of demand versus supply (with buffer). Finally, the better realization design would be able to be obtained by the class of eigenvalue or progressive type under certain indications of eco-entropy class concept, and also, a systematic unification of ternary SW/pair-map is geometrically realized at 3D type.
This approach on human-friendly and sustainable nature versus artifacts’ body may be incorporated into such the practical object of bodies (on vector space) as enterprise, economic structures, and SDGs, in the near future. Then, it is remarked as follows: the ideal artifacts science would ultimately need to confront the increasing entropy on DX-type issues at nano age.
Today, our world is facing the negotiations deadlocked on United Nations. Thus, the forthcoming world of SDGs would be much more constructive, that can transform its traditional body based on the 3M & I class (huMan, Material, Money & Information), as a nano (gene/therblig)-transformation towards eco-entropy (marginal value/diversity) on earth.
This semi-visible world is traditionally limited to a molecular size, and is too rough at the practical rig level. Thus, any unsolved and invisible contradictions (angle) such as the SDGs subject are left behind on this earth, in the practical or life world. Finally, we would like to propose the visible method that could find and solve these contradictions, by transforming the artifacts’ body consisting of 3M & I gene, in the near future.
Currently, the pair-map microcosm and its M-equation have been prepared mainly from nature and artifacts science books (Matsui, 2016, 2019) . Through these visible methods, the subject of our well-being might make a breakthrough or sublate the unsolved contradictions or stalemate, as any SDGs society of individuals. Therefore, from the advances of artifacts science, we might be able to further corporate our human-friendly and sustainable science into enterprises, economic bodies, and SDGs bodies on vector space.