Influence of Radial Dimension and Electric Field on a Microwave-Assisted Esterification ()
1. Introduction
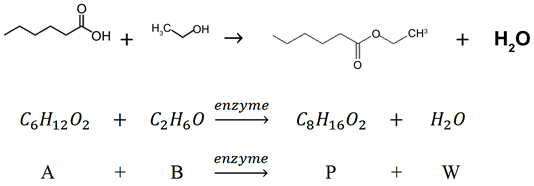
Like most short chain alkyl esters, ethyl hexanoate is characterized by a strong fruity flavor and fragrance, in this case, an apple-pineapple essence. Most of the flavors can be, of course, extracted from their natural sources but this implies high costs and low extraction yield; that is why organic synthesis is preferred. Esterification of a carboxylic acid with an alcohol, using sulfuric acid or para-toluene-sulfonic acid as catalysts, is a very common and simple way. However, this method cannot be used in food and pharmaceutical industries, in which enzymatic synthesis in a solvent-free system has huge market demand because they are labelled as “natural”, the final product quality is high and the reaction does not require much energy.
For this reason, the esterification of hexanoic acid (A) and ethanol (B) to ethyl hexanoate (P) with the enzyme Candida Antarctica lipase-B has been modeled.
The reaction kinetics has been shown to follow the Ping Pong Bi-Bi mechanism [1]. Optimum conditions to carry out this reaction are reached when the temperature is around 50˚C; the enzyme dose is about 2% w/w and molar ratio of acid to alcohol is 1:3 [2]. In order to maintain the temperature around the optimum value, as the reaction is endothermic (with the heat of reaction ΔHr = 23 KJ/mol), heating is required.
Since microwave heating allows reaching high conversions when used in organic synthesis [3], in this study, better operational conditions to perform such a process have been sought.
2. Mathematical Model
The physical system consists of a tubular reactor with length L = 30 cm and three different radial dimensions: R = 15 mm, 2R and 3R. The reactant mixture moves by the effect of a pressure difference between the inlet and the outlet section.
The mathematical model takes into account the time-dependent momentum, heat and mass balance equations, considering molecular and convective transport and the frequency domain Maxwell equations. For a cylindrical coordinate system (r, θ, z) is represented by the differential equations with the appropriate initial and boundary conditions [4], reported in Table 1.
The mass balance has been written for the reactant A. Concentration of B can be obtained by the stoichiometry of the reaction. The generation term is given by the reaction rate that follows the Ping-Pong Bi-Bi equation with inhibition by both substrates.
The generation term appearing in the energy balance, instead, consists of the sum of two terms: the heat absorbed by the endothermic chemical reaction and the heat provided by the microwave, expressed by the Poynting theorem, for both Eθ and Ez.
Initial conditions, obviously needed only for the equations in the time domain, state that at the beginning the system does not contain the reactants and it is at room temperature.
As regards boundary conditions, on the axis (r = 0) the symmetry condition applies for all the phenomena; on the external wall (r = R), thermally isolated and impermeable, the z component of the velocity is zero while both θ and z component of the electric field assumes a known and finite value different from zero (1300, 2600 and 3900 V/m for the tube of 1.5, 3 and 4.5 cm, respectively); in
![]()
Table 1. The mathematical model with initial and boundary conditions.
the inlet section (z = 0) the reactant A enters the tube with a concentration value CA0 (CB0 = 3CA0) at the same value of room temperature as the initial one; finally, in the outlet section, Dankwerts condition applies both for energy and mass equations.
3. Material and Methods
All the physical properties appearing in the mathematical model have been found in literature or experimentally determined. In some cases, both solutions have been adopted and results have been compared.
Physical properties can vary with temperature and composition: each of them refers to the mixture made up of reactants and products, so it is calculated as an average weighted on the molar fraction of each component present in the solution at a certain temperature (in the range considered, i.e., about 30˚C - 50˚C); therefore, it has been necessary to determine all the properties of all the substances that are initially present (hexanoic acid and ethanol) or are formed during the process (ethyl hexanoate and water).
Thermodynamic and transport properties such as densities, specific heats, thermal conductivities and viscosities of all substances can be found in technical manuals [5].
Dielectric properties (dielectric constant ε' and dielectric loss ε'') have been considered at the frequency used in the model (915 MHz).
Those water and ethanol have been largely investigated and so they can be easily found in the literature [6] [7].
Much less can be found instead about hexanoic acid and its ester. For this reason, it has been preferable to measure it on a small number of samples with HP 850708 dielectrometer, a network analyzer system available in the Microwaves and Optical Technologies Laboratory (MOTLab) in Industrial Engineering Department, University of Salerno.
The instrument can range from 200 MHz to 20 GHz of frequency and −40˚C
![]()
Figure 1. Dielectric properties of hexanoic acid (top) and ethyl hexanoate (bottom) as temperature functions.
and 200˚C of temperature, but measures have been performed from 850 to 950 MHz, being the frequency of interest equal to 915 MHz, and from 20˚C to 60˚C.
After calibration with water, the coaxial probe was immersed in some beakers containing first hexanoic acid and then ethyl hexanoate, in turn, placed in a thermostatic bath to regulate the temperature. Particular attention has been paid during this operation to avoid trapping bubbles under the probe and to keep it away from container walls. At this point, many measures at different temperatures have been performed. The collected data have been analyzed and elaborated to obtain the following relationship between dielectric properties and temperature (Figure 1).
It can be noticed that dielectric loss slightly increases with temperature for both materials; on the other hand, dielectric constant of the acid increases, while dielectric constant of the ester decreases with temperature.
4. Results and Conclusion
The ordinary differential equations, both Eθ and Ez components, have been solved analytically, applying the boundary conditions written above [8]. The other partial differential equations have been solved numerically by the finite element method, using the software Comsol Multiphysics®, version 5.6. Results in terms of concentration and temperature, to compare the effects of the two different field component and the three different radii, are reported in the following steady-state maps.
Figure 2 and Figure 3 show the steady state concentration (a, c, e) and temperature (b, d, f) maps in the three different reactors, stressed respectively with the Ez component and Eθ component of the electric field, applied in the same position, i.e., on the lateral surface.
It can be noticed that the concentration maps are similar when the systems are stressed with the same component of the electric field while, when stressed with distinct components, they differ from each other increasing the dimension of the three reactors.
As regards the temperature maps, the differences, already evident when the systems are stressed in the same way, increase according to the different stress and dimension of the three reactors.
In particular, steady state maps show that the concentration of A (hexanoic acid) becomes lower along the axis of the three tubes by the effect of the chemical reaction, with an almost complete conversion in the 15 and 30 mm radius reactors. Temperature is affected both by the endothermicity of the reaction and microwave heating. The latter is different in case a zeta or a theta component of the electric field is applied, causing a different temperature distribution and also a slight difference in concentration profiles due to the fact that physical and transport properties are temperature-depending.
As regards the hexanoic acid concentration profiles (Figure 4 and Figure 5), taken into consideration in the outlet section (z = L), they basically follow the parabolic velocity profile along the radius, in all three cases considered; along the
![]()
Figure 4. Concentration profiles along r and z parametric in time for the three reactors when Ez is applied.
![]()
Figure 5. Concentration profiles along r and z parametric in time for the three reactors when Eθ is applied.
z-axis in the center of the pipe; instead, the concentration profile decreases linearly from the initial value until the zero value is asymptotized at the outlet section.
Temperature profiles are affected by the power produced the microwaves and by the thermal power absorbed by the endothermic reaction.
In particular, when the system is stressed with the Ez component of the electric field applied to the lateral surface of the tubes, the generated power (Poynting’s modulus) decreases monotonously from the maximum value in the center (r = 0) until zero on the lateral surface (r = R), in the case of the smallest pipe (R = 15 mm); by increasing the size of the system and, therefore, the applied stress, the power generated by the microwaves decreases more and more rapidly and then oscillates, dampening around the zero value on the lateral surface; naturally, the oscillations increase with the radius of the tube. The power subtracted from the endothermic reaction is always less than that produced by microwaves, so the temperature profile follows the profile of the generation produced by microwaves.
In the case of the 15 mm pipe, the temperature profile decreases from the center until it is asymptotize to the final value on the lateral surface; for the 30 mm pipe, the temperature profile decreases from the center to about the middle of the pipe and then increases to the isolate side surface; finally, in the 45 mm tube, the temperature profile decreases up to a third of the radius and then reaches, through small oscillations, the final value on the wall with a flat profile.
Along the axial direction, the generated power is constant and greater than the generation subtracted from the reaction, except in the case of the 3 cm tube where the value of the generated power is equal to the average value of the power subtracted from the reaction. It follows that along the z-axis, the temperature profile is always increasing, first slowly and then rapidly, except for the intermediate-sized tube in which the temperature profile first decreases and then increases (Figure 6).
On the contrary, by stressing the system with the Eθ component of the electric field on the lateral surface of the systems considered, the generated power (Poynting’s modulus) increases monotonously from the zero value in the center (r = 0) up to the value on the isolate lateral surface (r = R), passing through a maximum at r = 1.25 cm in the case of the smallest pipe (R = 1.5 cm); by increasing the size of the system and, therefore, the applied stress, the power generated by the microwaves increases more and more rapidly and then oscillates, dampening around the zero value on the lateral surface; of course, the oscillations increase with the radius of the tube. The power subtracted from the endothermic reaction is always greater than that produced by microwaves, so the temperature profile is more affected by the endothermicity of the chemical reaction. The thermal profile, therefore, always increases in the case of the smallest pipe, always remaining below the initial temperature; increasing the size of the pipes, it increases, decreases and rises again below the initial temperature in the case of the intermediate pipe, while the oscillations always remain above the initial temperature in the case of the larger pipe.
![]()
Figure 6. Temperature profiles alongr and z parametric in time for the three reactors when Ez is applied.
![]()
Figure 7. Temperature profiles along r and z parametric in time for the three reactors when Eθ is applied.
Along the axial direction (r = 0), the generated power is equal to zero in all three cases, so the thermal profile always decreases below the initial temperature since there is only absorbed power and no generated power (Figure 7).
Acknowledgements
The Authors would like to particularly thank Professor Scaglione and Professor Chiadini for the possibility of using the instrumentations present in MOTLAb and the support in the measures of dielectric properties.