1. Introduction
In the classical (Newtonian) problem of the motion of a mechanical system with N degrees of freedom, we find—within a fixed time interval—the solution to the differential equation,
, (1a)
satisfying the initial conditions,
. (1a)
In the initial problem so formulated, it is assumed that the function
is continuous and that it satisfies the Lipschitz condition for the second and third arguments. Then, there exists a conclusive solution describing the motion of the system and the function X is continuous and double differentiable, that is,
.
Non-smoothness of the problem of motion implies that the function f is discontinuous or non-differentiable with respect to its second or third argument. A problem of this kind applies, for instance, to mechanical systems with unilateral constraints or with dry friction forces. In the monograph [1] where a system with unilateral constraints is analysed it is demonstrated that the solution to the problem exists within the class of absolutely continuous functions
. This means that the derivative
is discontinuous, and, an additional task specifying discontinuous changes in velocity needs to be formulated.
In the further considered non-smooth wheel motion problem, we investigate non-ideal unilateral constraints. The said non-idealness implies that the reaction force of constraints is combined with the dry friction force perpendicular to the reaction force. A hypothesis of this kind was put forward at the close of the 19th century by Painlevé [2] [3]. The contemporary analysis of this problem is based on the fundamentals of the non-smooth analysis presented in works by Jean, Moreau and Panagiotopoulos [4] [5] [6] [7] [8], and in works by the authors of this paper on machine and vehicle modelling, for example [9] [10] [11]. One should also mention contemporary studies [12] [13] [14] in which a singular problem known as the Painlevé paradox, widely discussed at the beginning of the 20th century by Prandtl, Hamel, Klein and Mises [2] is considered.
In relation to the above-mentioned studies, in this study we consider a specific method of description of motion with non-ideal unilateral constraints, suited for analysing a relatively simple problem relating to planar motion of a rigid wheel. The problem defined in this way fully illustrates the non-smooth issues of unilateral constraints while allowing leaving out a situation in which the Painlevé paradox occurs.
In addition to formulating the motion problem, we propose a method for determining the solution to this problem and present the results of wheel motion simulations.
2. Geometric and Kinematic Characteristics of the System
We consider a non-deformable wheel whose motion in the gravitational field is constrained by non-deformable planes with rough surfaces. Figure 1 is an illustration of the analysed system, with three coordinates describing the motion of the wheel, that is:
—the coordinates of the wheel’s centre point, S and
—the rotation angle of the wheel.
The motion constraints in Figure 1 are shown by the bold line representing the boundary of the area of the admissible positions of the wheel on the plane
. Figure 1 shows also the main dimensions of the boundary line and of the wheel, i.e.
, given that we are considering the case, when
and
. The gravitational field vector g is also marked.
It follows from the preliminary analysis of Figure 1 that the constraints under consideration can be specified by the area of the admissible positions of the centre point of the wheel, since the third coordinate, i.e. the wheel rotation angle
, is not constrained.
Based on the geometrical analysis of Figure 1 we determine the description of the said constraint in the form of the relation
, (2)
where the set
, specifying the area of the admissible positions of the centre point of the wheel has the form
, (3)
if the function
is specified as
, (4a)
where
,
(4b)
. (4c)
Figure 2 shows the set of points
with the interior of the set
marked in grey, i.e.
, and its boundary marked with the dashed line
. The
![]()
Figure 1. Geometrical representation of the considered wheel–constraints system.
descriptions of these sets have been established based on Equations (3) and (4), i.e.
(5a)
. (5b)
Furthermore, Figure 2 shows also the positions of the wheel in selected sectors of the boundary
. A more detailed graph of wheel positions in all the characteristic sectors of the boundary
are shown in Figure 3.
For the description of a constraint to motion to be complete, apart from the set
, we need to establish also kinematic implications, which follow from the relation (2) and will be referred to as its consequences. In the study [3] the author considered in detail the consequences, which determine the sets of admissible velocities and admissible accelerations.
If the wheel (cf. Figure 2) is in such a position that
, i.e. when the wheel is not in contact with the boundary of a constraint, then the above-mentioned kinematic constraints do not occur, and the wheel is moving freely.
![]()
Figure 2. Graph of the set
and its boundary
and a number of specific positions in which the wheel is in contact with the boundary of constraint.
![]()
Figure 3. Six specific positions in which the wheel is in contact with the boundary of constraint.
When the wheel makes contact with the boundary of a constraint, i.e.
, the velocity of the centre point of the wheel
is constrained, as it should satisfy the relation
, (6)
where
is the mapping referred to as the first consequence of relation (2). The definition of the mapping is given in [1], while a detailed description of this mapping in the problem under consideration will be provided further in this paper.
If the position and velocity of the centre point of the wheel satisfy the relation (6), then the acceleration of the centre point of the wheel can also be constrained. However, if
, (7)
then such a constraint does not arise, as the wheel making contact with the boundary of constraints moves away from it.
A limitation to the acceleration of the centre point of the wheel arises when the wheel makes contact with the boundary of the constraint and the velocity of the centre point of the wheel belongs to the boundary of the set of constraints to velocity
, i.e. when
. (8a)
In such a situation the wheel making contact with the boundary of constraint can either roll on it or remain still. Then the acceleration of the centre point of the wheel
is constrained, as there should be satisfied the relation
, (8b)
where
is the mapping referred to as the second consequence of the relation (2), determining the set of the admissible accelerations of the centre point of the wheel. A definition of this mapping is provided in [1] and a detailed description referring to the wheel will be given further in Section 3.
In the situation specified by Equation (8a), the constraints are acting, which means that the reaction force, which will describe further on, is arising out of them. During the motion of the wheel there can also occur a situation when the position and the velocity of the wheel are such that
, (9)
which means that the velocity of the wheel is not admissible due to constraints, as it does not satisfy the condition (6). In this state, the wheel collides with rigid constraints. During the collision the velocity of the wheel changes sharply (abruptly) and reaches a value, which satisfies the relation (6). The formula describing the change in velocity during the collision will be presented further on in the paper.
As mentioned before, the consequences
and
specify the sets of admissible velocities and accelerations of the wheel making contact with the constraining surface (Figure 1). The principles of determining these mappings have been described in detail in [1] [9]. Taking into account the relatively simple form of the boundary of the set
(Figure 2), we will determine the descriptions of these mappings in the form which requires no explanation.
3. Model of the Action of Constraints on the Wheel
An action of a constraint on the wheel occurs when the wheel comes into contact with the constraint. In this position, there can be generated a reaction force acting on the wheel, which we will discuss in detail further on in the paper.
Figure 4 is an example illustration of a wheel making contact with a plane constraining its motion at point A. A local coordinate system Ant, whose axis An is perpendicular, and axis At is tangent to the boundary
, is marked in the figure; also the velocity of the point A situated on the circumference of the wheel is shown in it. Due to the constraints to the motion of the wheel, the normal component of this velocity should satisfy the condition
. (10)
The velocity for which
is in admissible due to constraints; in this situation a collision occurs, which will be considered further on in this paper.
If
, then the constraints do not limit the motion of the wheel, as the wheel moves away from the boundary.
Figure 4(b) shows the vector of acceleration of the point A.
If the velocity of point A is such, that
, then the constraint forces are acting on this acceleration
. (11)
In the above-described situation, there arises the reaction force illustrated in Figure 4(c). In the case of ideal constraints only contact force
is acting, while the tangential component,
is not generated.
For non-ideal constraints a hypothesis is assumed according to which the tangential component maps the force of friction between the wheel and the boundary of constraints. The non-ideal constraints model so specified is described by relations, which determine the relationship between the reaction force R and the acceleration and velocity of the point A belonging to the wheel:
![]()
Figure 4. Velocity, acceleration and reaction vectors acting on the wheel making contact with the boundary of the set
at the point A.
- for the normal component
we have:
, (12a)
- while the tangential component
, when
, is specified by the relations:
, (12b)
, (12c)
where
—the coefficient of friction between the wheel and the boundary of constraints;
—the friction multiplier.
The above relations can be illustrated with graphs; Figure 5(a) represents a graph of the relation (12a), while the relation (12c) is shown in Figure 5(b). Furthermore, the relation (12a) (Figure 5(a)) can be equivalently described by the relationship:
, (13a)
where
denotes such a function, that
. (13b)
Likewise, for the relation (11c) (Figure 5(b)) we obtain
, (14a)
where the function
has been defined as:
. (14b)
In the above-presented hypothesis on the interaction between non-deformable bodies in contact we have not taken into consideration the moment of forces, referred to as rolling resistances of the wheel. This is the moment of friction, the limit value of which is proportional to the contact force
. The direction of this moment is opposite to the angular velocity of the wheel. In order to simplify the description of the reaction force acting on the wheel, and assuming that the value of rolling resistance is very small, we have disregarded their effect on the motion of the wheel.
![]()
Figure 5. Graphs of relations (12a) and (12c).
Now we will consider a situation when the wheel collides with the constraints, that is when
. Schematic descriptions of the wheel’s velocities immediately before the collision
and after the collision
are shown in Figure 6(a) and Figure 6(b), while Figure 6(c) represents the reaction force impulses,
and
, inducing the change in the velocity of the wheel. The friction impulse
is determined according to the Routh’s hypothesis [3].
The already mentioned effect of the collision is described by a relation between the post-collision velocities
(Figure 6(b)) and the reaction impulses (Figure 6(c)). This relation is formulated in accordance with the assumed hypothesis. For instance, when smooth (ideal) constraints are analyzed, the tangential component, that is
is disregarded.
In this paper, we will present a description of the hypothesis on plastic collision, and on elastic collision or elasto-plastic collision, based on the assumption that the constraints are non-ideal.
A description of the plastic collision has a form analogical to the description of the reaction force, as given in the formulae (12). The plastic collision is specified by the relations:
, (15a)
. (15b)
The relation (15b) has been determined based on the Routh’s hypothesis [3].
Graphs illustrating these relations are analogical to those shown in Figure 5 and they can be presented in an equivalent form, analogically to the formulae (13) and (14).
The description of the plastic or elastic-plastic collision is based on the Newton’s-Poisson’s hypothesis analyzed in [1]. According to this hypothesis the resultant reaction force impulse during such a collision is specified by the formulae:
, (16a)
, (16b)
, (16c)
![]()
Figure 6. Velocities and impulses acting on the wheel colliding with constraints.
where
,
—impulses described in the formulae (15);
—the coefficient of restitution, whose value for the elastic collision is 1.
4. Description of the Motion of the Wheel
The motion of the wheel will be described in the matrix form, using generalized coordinates. To this end, we introduce the following designations:
—generalized coordinates vector,
—wheel inertia matrix,
—vector of the gravitational force acting on the wheel,
—vector of the reaction force perpendicular to the boundary of the set
,
—vector of the reaction force tangent to the boundary of the set
,
—relations describing constraining of the motion of the wheel.
If the position of the wheel is such that
, then the constraints do not act and the motion of the wheel is described as:
, (17a)
and if the motion of the wheel is constrained, which may occur when
, then the equation of motion should include a description of reaction forces
. (17b)
In the next section of the paper we will define the method of determining the reaction forces.
4.1. Determination of Reaction Forces
In the descriptions of constraints and reaction forces presented further in the text we will use vector functions G and H, which to each vector X satisfying the relation
assign a pair of vectors, namely the perpendicular vector,
and the tangent vector,
. With these vectors we can determine the velocities and acceleration of the point on the wheel in contact with the boundary of the set
(See Figure 3),
, (18a)
, (18b)
where
and
are scalar functions. Detailed forms of the vector functions, G and H, and scalar functions,
and
, will be given further on in the paper.
Using the functions, G and
one can describe the consequence
, according to formula (6), determining the set of admissible velocities
,
, when
(19a)
and the set of admissible velocities according to the formula (8b),
,
when
and
(19b)
If the position X and the velocity
satisfy the relations specified in formula (19b), then the reaction force F occurs, whose two components
and
are present in the equation of motion (17b).
We will describe the generalized reaction forces
on the basis of the relations given in formulae (12). The normal reaction force is determined by the formula,
, (20a)
if
is the multiplier of the reaction satisfying relations resulting from the formula (12a), that is
(20b)
If we take into account the description of relations from the formula (11), we will obtain an equivalent description,
, when
and
, (21)
if
is any positive number.
Likewise, according to the formulae (12b) and (12c) we determine relations describing the tangential reaction
,
(22a)
, when
(22b)
, when
, (22c)
if the vector
has been described in the formulae (18b).
In the formula (20a), we have taken into consideration the fact that the load exerted by the wheel on the boundary of constraints, specified by the force from the formula (20a), is
(23a)
and the resulting friction force limit (the Coulomb’s limit) is equal to
. (23b)
The relation between the multiplier
and the acceleration
given with the formula (22c) can be presented, analogically to the relation (21), in the form:
, when
, (23c)
where
is any positive number.
4.2. Wheel Acceleration
The equations of motion represent a set of relations based on which the wheel acceleration vector
can be determined at any instant of time
, provided that constraints of motion are satisfied, that is when
and
.
If the wheel is in contact with the boundary of constraint, that is when
and
, (24)
then the constraint reaction forces considered in the previous section are acting on the wheel.
On this basis we formulate a set of relations from which the value of the acceleration vector can be unequivocally determined. The set includes:
- the equation of motion (17b), which includes the expressions (20a) and (22a)
(25a)
- the relations specifying the multipliers according to the formulae (21) and (24)
(25b)
, (25c)
however, in the formulae (25) the arguments of the mappings G, H,
and
have not been specified.
Equation (25) determine at any moment in time
, the value of the acceleration vector
and the values of multipliers
and
, which specify the values of the reaction forces.
The relations (25) comprise the mappings G, H,
and
, the descriptions of which will be given in the next section.
4.3. Description of Additional Mappings
The mappings G, H,
and
given in the previous section of the paper serve as a description of the geometrical features of the boundary of constraints
, with the use of generalized coordinates. As mentioned before, the vector mapping G determines, in each point of the boundary
, the vector
, which is perpendicular to to the boundary of constraints, and the mapping H determines the vector
, which is tangent to it. The scalar mappings,
and
serve to determine the effect of the curvature of the boundary and of the velocity of the wheel on its acceleration.
The considered boundary of the set is presented in Figure 2. It is composed of four segments, including two singular points A and B (cf. Figure 7).
The description of the mappings under consideration depends on the curve segment and follows from the formulae (3) and (4). Hence, we obtain:
- Segment I,
(26a)
- Segment II,
(26b)
- Segment III,
(26c)
- Segment IV,
(26d)
In the formulae (26) we have used designations marked in Figure 2 and associated with the function f, described in the formula (4c). Thus, we obtain:
(26e)
The singular positions of the wheel are specified by the wheel centre point coordinates, i.e.
![]()
Figure 7. The boundary of the set
with marked segments and singular points.
(27a)
. (27b)
In these positions the wheel comes into contact with the constraints at two points (Figure 8).Thus, the resulting descriptions of the sets of admissible velocities are as follows:
(28a)
, (28b)
where designations from formulae (26) have been used.
As mentioned before, a constraint to the wheel’s acceleration and a reaction force arise when the velocity vector is situated at the boundary of the set
, which has been described in the formulae (19) and (20).
On this basis, we specify the relations for the normal component of the reaction force in the position A (27a)
. (29)
Values of the multipliers
and
are connected with the vector of acceleration
by the relation described in the formula (25b).
The force of reaction
, acting on the wheel in position B (27b) is calculated analogically to the formula (29), i.e.
(30)
The form of the description of the relations between the multipliers
and the vector of acceleration
has been specified by the formula (25b).
The tangential component of the reaction force
will be specified based on
![]()
Figure 8. The singular positions in which the wheel makes contact with the constraints at two points.
the relation (22), but after taking into account the proper indices of the vectors G, H and of the multipliers
,
.
5. Description of the Collision
In the situation specified by the relation (9), the velocity of the wheel is inadmissible due to constraints, which results in a collision. As a result, there occurs an impulse reaction of the constraints, adjusting the wheel’s velocity to the limitations. In section 3 we have presented a local description of the collision model, in the form of a relation specifying the association between the impulse reaction and the abrupt change in the velocity of the wheel. We will now present the relations described in that section using the generalized coordinates.
Description of a plastic collision includes also the momentum balance equation and the relations specifying the impulse reaction forces. The general form of this description is analogical to the equations of motion (17) and (25), i.e.
(31)
(32)
and the description of the relations from the formulae (15) now has a form analogical to (25b) and (25c), i.e.
(33a)
, (33b)
where the force impulses acting on the wheel have been marked with the index “~”.
When the collision of the wheel with the constraints occurs in the singular position of the wheel specified by point A or B (according to the formulae (27)), then two reaction forces are acting on the wheel, i.e.
for point A, (34a)
for point B. (34b)
The relations specifying the multipliers,
and
, from the formulae (34), have the same form as in the formulae (33) but after taking into account the suitable indices.
As mentioned before, the relations from the formulae (32) and (33) specify an abrupt change in the velocity of the wheel
, and the reaction force impulses,
and
, arising during the plastic collision.
If an elastic or elasto-plastic collision is considered, then—according to the Newton’s and Poisson’s hypothesis specified by the formulae (16)—we need to take into account an additional collision phase (restitution) described by the equations
, (35a)
where
—the velocity vector after the elastic or elasto-plastic collision;
,
—the reaction force impulses generated in this phase, specified by the relations:
,
, (35b)
,
. (35c)
In the above relations, the value of the multiplier
is known, which follows from the formula (35c), where
is the coefficient of restitution, the value of which for the elastic collision is 1.
Relations (35) determine the velocity vector after the collision
and the multiplier
, specifying the effect of friction on this collision phase.
6. Wheel Motion Simulation
6.1. Description of the Method of Solving the Initial Problem
The non-smooth problem of a mechanical system motion was closely analyzed in the monograph [1], where perfect unilateral constraints were considered. It follows from these considerations that the motion of such system is described by an absolutely continuous function. A staged method of determining such a function was also specified in this work. We will use this method to determine the function describing the motion of the wheel.
The descriptions of the relations considered in sections 4 and 5, specifying the motion of the wheel will be now presented in a synthetic form by means of two equations,
(36)
, (37)
where
—the vector of the generalized coordinates,
—the mapping determining the vector of acceleration,
—the mapping determining an abrupt change in velocity in the moments of collisions.
The mapping
is specified in the implicit form by means of the relation (25). In this case, determining the value of the mapping
comes down to determining the solution of the relation (25), i.e. to calculating the values of multipliers
and
, and of the vector
.
The mapping
is also implicit and its values are determined by the solution to relations (32)-(35), specified by the multipliers
and
and the vector
.
At every stage of the above-mentioned method the solution of the initial problem specified by Equation (36) is determined. The continuous and differentiable function X so established, describes the motion of the wheel up to the moment when the collision specified by the conditions from the formula (37) occurs. Then an abrupt change in the wheel’s velocity described by the mapping
takes place. In this situation the considered stage of the solution comes to an end.
This staged method of finding the initial problem solution has served as a basis for developing calculation software for wheel motion simulation. The program includes algorithms for determining the values of implicit mappings
and
, in all segments of the set
described by the formulae (26) and at all singular points (27) designated in Figure 7. It needs to be added, that in order to determine the values of the implicit mapping
, it is necessary to solve a system of algebraic equations containing five unknowns:
,
and
. The values of the implicit mapping
are determined in the same way.
6.2. Detailed form of the Equations of Motion and Reaction
To start with, we will consider the detailed form of equations of motion and reaction, when the wheel makes contact with the boundary of constraints in sector IV (See Figure 7). In Figure 3 the wheel with index 6 illustrates such a position. In the considered situation, the conditions specified in the formula (24), that is
,
and
are satisfied, where a,
—dimensions described in the formula (4b).
The equations of motion (25) in expanded form, and after taking into account the formulae (26d), for sector IV, have the form:
(38)
(39)
(40)
(41)
. (42)
The above system of equations describes the accelerations of the wheel (
,
,
), and the multipliers of reactions (
,
). This is an implicit form of the mapping
, when the wheel is in contact with the boundary of sector IV. Determining the solution to the above system of equations is relatively simple:
- if the wheel is slipping, i.e.
, then the value
is determined directly from Equation (421);
- if the wheel is rolling without slip, then from Equations (422) and (38) and (39) we obtain that
;
- from the relatively simple system of Equations (39) and (41) we obtain
;
- having determined the values,
and
, from Equations (38), (39) and (40), we can determine acceleration values, and in particular we have
.
The above-described Equations (38)-(42) apply to motion of the wheel moving (rolling) on the boundary. Now, we will deal with describing a collision of the wheel with the boundary in sector IV.A general description of the collision has been given in the formulae (32), (33) and (35). In the considered situation the expanded description of the collision, assuming the plastic collision hypothesis, has the form:
(43)
(44)
(45)
(46)
(47)
. (48)
This is a system of equations in regard to
,
,
,
. The solution is determined in the following steps:
- from Equations (44) and (46) we can directly determine
;
- according to the formula (48) and Equations (43) and (44) we obtain the relationship,
, (49)
and next, from Equation (47) we determine the values,
and
;
- having determined the values,
and
we calculate the post-collision velocities,
and
.
The solution determined specifies the effect of the plastic collision. When considering an elastic or elasto-plastic collision it is necessary to take into account the change in velocity in the second phase of the collision, described in the formulae (35). In the example under consideration, this description, with respect to the coefficient of restitution
, has the form:
, (50)
, (51)
, (52)
(53)
, (54)
. (55)
The effect of the collision is described by the velocities
,
,
and multipliers
and
. The value
is specified by the formula (50), while the values
and
are obtained directly from the formulae (54) and (55).
During the motion of the wheel in sector III (cf. Figure 6), the wheel makes contact only with the corner of the curb, which is illustrated in Figure 3 (the wheel with index 4). In this case the centre point of the wheel takes the position specified by the conditions (see formula (26c)),
,
(56a)
and the velocity of the wheel is such, that
. (56b)
The condition (56b) indicates, that the normal component of the velocity of the point on the wheel (Figure 3 and formula (10)) making contact with the constraints equals zero, i.e. the wheel does not get separated from the curb.
In the formulae (26c) we included definitions of the vectors G and H and expressions
and
. To simplify further descriptions we will omit indices “III” present next to the enumerated designations.
For the wheel status so specified (formulae (56a) and (56b)), we formulate an expanded description of the wheel’s acceleration and constraint reactions according to the formulae (25):
, (57)
, (58)
, (59)
, (60)
, (61)
where the following designations have been introduced:
, (according to the formula (26c)) (62)
—the contact force exerted by the wheel on the curb,
—the tangential component of the velocity of the point on the wheel in contact with the curb,
(63)
—the normal component of the acceleration of the point on the wheel in contact with the curb
, (64a)
from the condition of constraints (11) it follows that the value of this acceleration may be greater than or equal to zero. If in the formula (64a) we include Equations (57) and (58), we will obtain:
(64b)
—the tangential component of the acceleration of the point on the wheel n contact with the curb,
, (65a)
if in the above equation we include Equations (57), (58) and (59), and make suitable transformations, we will obtain:
. (65b)
To determine the value of multiplier
we need to substitute the expression
into Equation (60) according to the formula (64b); from this we can directly calculate the value
.
When the value of the velocity of the wheel’s slip on the curb
(according to the formula (63)) is different from zero, then from the formula (611) we obtain the value of the multiplier
. If
, then we should substitute the expression
into Equation (612) according to the formula (65b); in this way we obtain the value of the multiplier
.
Having determined the values of the multipliers
and
we calculate the values of the accelerations
,
and
according to the formulae (57), (58) and (59).
The collision of the wheel with the curb occurs when the velocity
according to the formula (56b) is negative, i.e.
(See Figure 3(a)). The effect of this phenomenon, on the assumption of the plastic collision hypothesis, is described by the equations:
(66)
, (67)
, (68)
, (69)
. (70)
Solving these equations in regard to
,
,
,
,
determines the velocity of the wheel after the plastic collision and the reaction force impulses. To determine the solution, we establish the expressions specifying
and
, depending on the multipliers,
and
.
(71)
(72)
Having included the formula (71) in Equation (69), we obtain the value of multiplier
. Next, from Equation (70) and from the relationship (72) we determine the values,
and
. Having determined the multipliers we calculate the values of velocities looked for after the plastic collision,
,
and
.
If we consider an elastic or elasto-plastic collision, we should consider a description of the second phase of collision (35), analogical to the formulae (50)-(55),
,
(73)
(74)
, (75)
, (76)
, (77)
. (78)
Based on Equations (77) and (78) we can directly determine the value of the multiplier
, and subsequently the values of the wheel’s velocity.
If the wheel assumes the singular position specified by point B (Figure 8), then the description of the action on the wheel becomes more complex, as the wheel makes contact with constraints at two points B1 and B2 marked in Figure 8. The position of the wheel is determined by the coordinates of the wheel’s centre point,
,
, while the description of the set of the admissible velocities of the wheel at this position is as follows:
, (79)
where
—the value of the derivative of the function f for
,
(80)
Figure 9 shows a schematic graph of the set
.
It is clear from an analysis of Figure 9, that in the considered position the constraints are acting, that is they are limiting accelerations, only when the velocity vector belongs to the boundary of the set
, which is written in the formula (8a). Figure 9 shows three examples of velocity vectors
situated on the boundary. For the vectors
and
, only one constraint is acting, while for the vector
both constraints are acting.
The action of individual constraints has been described before, and now we will deal with the situation specified by velocity
that is, situation when
and
. It follows from these conditions, that the translational
![]()
Figure 9. Graph of the set
in the singular point B (cf. Figure 7).
velocity equals zero, but we assume that the wheel is rotating, i.e.
. In this situation the wheel is slipping on the constraints.
In the state described above the acceleration of the wheel is constrained, and the set of admissible accelerations has the form
. (81)
The equations specifying the acceleration and reaction forces now have the form:
(82)
, (83)
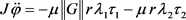 , (84)
, (84)
, (85)
, (86)
where the reaction multipliers acting on the wheel at points
showed in Figure 7 are marked as
,
, for
; and
,
—normal components of the acceleration of the wheel at points
and
.
,
(87)
Since we have assumed that
, then
(88)
On the basis of the above equations we should determine the values
,
,
, and
and
. To this end, from the formulae (87) and Equations (82), (83) and (84) we establish the expressions:
. (89)
. (90)
Upon substituting the expression (89) into the formula (85) and assuming
, we obtain
, if
. (91)
Likewise, from Equations (90) and (86), when
, we obtain
, if
. (92)
The solution of Equations (91) and (92) determines the values of multipliers
and
, while the values of accelerations
,
,
are calculated from the formulae (82), (83) and (84) after taking consideration (88).
It follows from an analysis of Equations (91) and (92) that, if
, i.e.
, then (93a)
,
, (93b)
that is an obvious result is obtained—the wheel moves away from the curb, that is
,
,
.
If
, i.e.
, (94a)
then two solutions are possible:
,
, when
, (94b)
,
, when
. (94c)
In the case specified by the formula (94b), the centre point of the wheel is not changing position
, but the wheel is rotating
,
(spinning); while in the second case (94c) the wheel is climbing the curb, because
,
.
In the considered position of the wheel, a collision with the curb occurs, when the velocities
and
fail to satisfy the conditions given in the formula (79), that is they do not belong to the set
whose graph is shown in Figure 8. The resulting plastic collision is described by the following relations, given in Section 5, in the formulae (32)-(34):
, (95)
, (96)
, (97)
, (98)
, (99)
, (100)
, (101)
where the following designations have been introduced:
,
, (102)
,
, (103)
,
, (104)
,
. (105)
From the above-given equations we should determine the velocities of the wheels after the collision
,
,
and reaction impulse multipliers
,
,
,
. Since it is a relatively complex system of nonlinear equations, an iterative method has been used to solve it. This method involves looking for a vector
, which satisfies the equation
, (106)
where
denotes a mapping specified by the right sides of the above-given equations.
When we consider an elastic or elasto-plastic collision, then based on Equation (35) we should formulate relevant relations taking into account detailed data specifying the state of the wheel at point B. On this ground we establish the following equations:
, (107)
, (108)
, (109)
, (110)
, (111)
, (112)
. (113)
On the basis of the above relations we can obtain two nonlinear equations in regard to
and
, which we solve by iteration. Having determined their values we can determine the values of acceleration after the second phase of the considered collision
,
,
.
The relations given in this subsection refer to determining the acceleration of the wheel and its velocity after the collision when the wheel is positioned in segments IV, II and III and at point B (Figure 7). We do not present equations for segment I, as they are analogical to the equations for segment IV; while the equations at the singular point A, are similar to the above-described equations for point B.
6.3. Results of Computer Calculations
We consider planar motion of the non-deformable wheel on which constraints presented in Figure 1, Figure 2 and Figure 6 are acting. The wheel motion simulation is performed assuming the following values of the wheel’s parameters: the mass
, moment of inertia
, and radius
. The dimensions represented in Figure 1 are
and
. Furthermore, we assume that the gravitational acceleration is
, and the initial conditions are defined with two vectors,
,
(114)
Based on the relations presented in section 4, sets of relations specifying the acceleration of the wheel and forces of reaction and relations specifying discontinuous changes in the wheel’s velocity induced by the collision have been established for each segment of the boundary of constraints (Figure 6).
The simulation of the motion of the wheel has been performed over the time interval
. We assumed the value of the coefficient of friction between the wheel and the boundary of constraints,
. Two tasks differing only with the value of the coefficient of restitution
have been considered. In the first task, the motion of the wheel has been simulated with the assumption of the hypothesis of plastic collisions
. In the case of the second task, we have assumed
, which corresponds to the elasto-plastic hypothesis.
The wheel position sequences during the simulation are illustrated in Figure 10 (plastic collisions) and Figure 11 (elasto-plastic collisions). The figures show also the initial conditions of the wheel. It follows from them that in the initial stage of its motion the wheel moves in a translational motion and after the first collision it starts rotating.
The next Figure 12 represents two trajectories (paths of the wheel in motion) followed by the centre point of the wheel in the two tasks under analysis.
The two last graphs illustrate the positions of the wheel’s centre point and the angle of rotation in time (Figure 13), as well as the speed of change of these values
![]()
Figure 10. The sequence of the positions of the wheel during simulation (plastic collisions).
![]()
Figure 11. The sequence of the positions of the wheel during simulation (elasto-plastic collisions).
![]()
Figure 12. Trajectories followed by the centre point of the wheel: plastic collisions (solid line), elasto-plastic collisions (dashed line).
![]()
Figure 13. Curves of wheel centre point positions (a) and (b) and of the rotation angle (c) over time: plastic collisions (solid line), elasto-plastic collisions (dashed line).
in time (Figure 14). The results illustrated in these figures reveal major differences in the behaviour of the wheel, depending on the collision hypothesis assumed.
7. Conclusions
An analysis of the non-smooth problem of the motion of a mechanical system in the form of a wheel with constrained motion has been presented in the paper. It has been demonstrated that the formulation of the non-smooth problem of motion encompasses relations determining accelerations of bodies and relations determining discontinuous changes in the velocity of the bodies induced by the
![]()
Figure 14. Curves of wheel centre point positions (a) and (b) and of the angular velocity (c) over time: plastic collisions (solid line), elasto-plastic collisions (dashed line).
collision. Descriptions of these relations have been established according to the hypotheses specifying interactions (reactions) between non-deformable bodies coming into contact.
In the wheel example under consideration, the interpretation of the assumed hypotheses is clear, and therefore the formulation of a non-smooth problem of motion is relatively simple. In the case of a rigid body in a three-dimensional space, the description of the reactions is more complex, and apart from that, it is impossible to unequivocally determine the acceleration and the reaction force for individual positions of the body. Such singular states of the system result from the approximate character of the hypotheses specifying the forces acting between the bodies in contact, which applies in particular to friction forces.
Non-smooth problems of motion expand on the body of classical problems of the theoretical mechanics, thus increasing the scope of modeling methods and simulation studies on the motion of and loads applied to machines, vehicles and components of engineering structures [15].