Relating Some Nonlinear Systems to a Cold Plasma Magnetoacoustic System ()
1. Introduction
Over the past years, points of connection of plasma physics to various nonlinear equations of significant importance have been explored. An initial connection can be traced back to H. Washimi and T. Taniuti [1], for example, who showed that the one-dimensional asymptotic behavior (as
) of small amplitude ion-acoustic waves was described by the Korteweg-deVries equation—following on a parallel track work of C. S. Gardner and G. K. Morikawa [2]. The paper of A. Jeffrey [3] provides for some systematic details on this particular connection, and it includes remarks, for example, on the work of Y. A. Berezin and V. I. Karpman [4].
In the 2007 paper [5] of J.-H. Lee, O. K. Pashaev, C. Rogers, and W. K. Schief the resonance nonlinear Schrödinger (RNLS) equation
(1)
appears in connection with a discussion of one-dimensional, long magnetoacoustic waves in a cold plasma subject to a transverse magnetic field
. Here
the field of real numbers with
, and
is a de Broglie quantum potential. For
, a complex-valued wave function solution
of the form
(2)
was obtained, where
is the plasma density and S is a real-valued velocity potential. That is, the velocity field u of the plasma is given by
. In the present paper we consider for an arbitrary
solutions of Equation (1) of the form
(3)
for real-valued functions
. Such a function
is a solution if and only if the pair
is a solution of the Madelung fluid system
(4)
independently of the assumption
.
The system of main interest for us is the nonlinear magnetoacoustic system (MAS)
(5)
which describes the propagation of the aforementioned magnetoacoustic waves in the cold plasma, under some simplifying assumptions that include the uni-axial propagation assumption
(6)
Here
and
are unit vectors along the x and z axes. The system (5) is derived by way of a shallow water type approximation of the system
(7)
where a change of variables
is employed (under which the first two equations in (7) are invariant and third one becomes
), and where an expansion of B of the form
(8)
is inserted into the second equation [5] [6] [7].
We will work with the following explicit traveling wave solution
of the MAS (5) given by A. Gurevich and A. Krylov (G-K) in [8]. For a choice
,
, define
(9)
where the second expression for C in (9) follows as
and
. Then for the standard Jacobi elliptic function
with elliptic modulus
[9]
(10)
The choice for
in (1) will be
. As shown in [10] (also compare [5] [7]), given a solution
of the MAS (5) and the assumption
, one can construct a corresponding solution
of the Madelung fluid system (4) where
(11)
and, moreover, a corresponding solution
of the reaction diffusion system (RDS)
(12)
where
(13)
In the present case of (10) therefore
(14)
As before, we see in (11) that S is a potential function for the velocity field u. Note also that by (3) and (11) we obtain the solution
(15)
of the RNLS equation (1).
The formulas (11), (14), (15) relate the nonlinear systems (4), (12) and the resonance nonlinear Schrödinger Equation (1) to the cold plasma system (5) with solution (10). In Section 2 we relate the solution (10) also to nonlinear systems of Broer-Kaup, Boussinesq, and Hamilton-Jacobi-Bellman and their anti-systems given by the time reversal
. Here we find solutions of these systems that generalized in a non-trivial way those found in [11], for example. By choosing
so that
, and choosing
so that
by (9) and
is a constant function in (10), in particular, our r in (14) and
in (34) of section 2 reduce to the dissipaton
and shock soliton
in Sections 2 and 4 of [11].
Attention in Section 4 is turned to further remarks on the cold plasma-2d black hole connection set up in [10]. The main result of that section is the computation of two more plasma dilaton fields such that these combined with the one computed in [10] form a linearly independent set. This too generalizes in a non-trivial way (namely the case
) a result found in [12].
Finally, in Section 5, we switch from the traveling wave solution
to a plane wave solution of the system (5). Remarkably, its dispersion relation coincides with the dispersion relation obtained from the linearization of the RNLS Equation (1) about a suitably normalized ground state solution
.
Throughout, an attempt is made to maintain an expository style in the presentation of the material, for the sake of completeness.
2. Elliptic Function Solutions of Broer-Kaup, Boussinesq, and Hamilton-Jacobi-Bellman Systems
In addition to the solutions (11), (14) of the Madelung fluid and RD systems (4), (12), and the RNLS solution (15) of (1), all of which were constructed by way of the G-K solution (10), we consider now solutions of nonlinear systems of Broer-Kaup (B-K), Boussinesq, and Hamilton-Jacobi-Bellman (H-J-B), and of their time reversal (
) systems. Here, again, the G-K solution (10) of the MAS (5) plays an underlying, subtextual role.
2.1. Conservation Laws and the B-K System
From the RDS (12), conservation laws can be deduced by which, in turn, one can derive the B-K system. We provide a sketch of this derivation, for the sake of completeness, and we present a general elliptic function solution.
The continuity equation
, or conservation law, in (5) is one of many such laws. The RDS (12) gives rise to the conservation law
, (16)
for example, for which the particular value
there does not matter. To check (16), start with the equation
. Multiply the first RD equation in (12) by s and the second one by r. Addition of these two multiplied equations eliminates B and gives the equation
, by (i), which is the assertion in (16).
In addition to (16), we also need the conservation law
, (17)
which also follows from (12). Namely, the l.h.s. in (17) is
, where the third term here is
(by (12))
. Thus the l.h.s. in (17) is
, by the equality of mixed partials:
and
. Equation (17) is now established.
Define
. (18)
For
and
, we see that
and similarly
, which says that the conservation law (16) can be written as
. (19)
Also by (ii), (iii),
, (20)
so that (19) and (20) together give the equations
,
, (21)
which suggests that one defines
,
: (22)
,
. (23)
Then
(by (12))
(by (18))
. That is,
. (24)
Similarly, by (12) and (18) again,
. (25)
Putting the pieces together, (Equations (23)-(25)), we have derived from the RDS (12), for
, and B arbitrary (not necessarily the specific value
there) the Broer-Kaup systems
(26)
for
and
defined in (18) and (22). The second system in (26) (with the minus signs) corresponds to the time reversal
.
We can obtain elliptic function solutions of the systems in (26) immediately, by way of the solutions
in (14). Note first that by (10), (14), (18)
(27)
Also by (14)
(28)
From [9], the identities and differentiation formulas
(29)
hold for the standard Jacobi elliptic functions
. The following is a useful inequality:
. (30)
By definitions (13), (11), (10), (9), respectively
(31)
By (10) (again)
(32)
so that the last differentiation formula in (29) gives
, (33)
which with (22), (28), (31) and (32) gives
(34)
for C given in (9).
The formulas (27) and (34) therefore provide for a solution
of the Broer-Kaup systems in (26). There we take
, since we used the specific solution
in (14) of the RDS (12).
The solution
of the first system in (26) vastly generalizes the one
found in [11], where the notation
there corresponds to
here, and where a solution of the second system in (26) is not addressed.
The generalization here is not simply that of elliptic functions over hyperbolic function, but it is in large part due to the freedom to allow
to be non-zero:
. Indeed for
, all results of this paper, and those of [10], simplify greatly—mainly because then
, by (9). For
, the formulas in (27) and (34), for example, reduce to
(35)
which, moreover, for
reduce further to
(36)
which apart from
are the results that appear in [11], with a different choice of constants—the
in (36) being the shock soliton mentioned in the introduction. We shall see in Section 3 that in case
, there is also a nice choice for the potential function
in (11), and thus a nice expression for
in (13), (14), and for
in (15) exists in this case.
2.2. Boussinesq Systems
Given the bulk of details and formulas in Section 2.1, we can glide more easily through this section. A good number of equations for various mathematical models are referred to as Boussinesq equations. It is perhaps best then to consider the systems discussed here more properly as Boussinesq type systems. This prolific French researcher, Joseph Valentin Boussinesq (1842-1929) made numerous high level contributions to fluid mechanics that involved the theory of solitary waves and the KdV equation, for example, and contributions to several other fields including the propagation of light and the theory of linear elasticity.
Define the “pressure” functions
by
. (37)
As before we will choose
. By (26),
(38)
so that
. (39)
One can compute
also, and in the end, with (39), derive the Boussinesq type systems
(40)
The second system in (40) (with the minus signs) corresponds to the time reversal
.
As with the B-K systems in (26), one can obtain explicit elliptic function solutions of the systems in (40), or simpler hyperbolic function solutions as in (36), by taking
. For this one simply applies the formulas for
and
in (27) and (34) to compute
in definition (37)—perhaps with the help of Maple. Generality in an alternate direction of importance is provided by Professor Pashaev in [11] who considers kink-soliton and two-soliton solutions of the Broer-Kaup and Boussinesq systems (26) and (40). These latter systems trace back to the analysis of water waves propagating in a long narrow channel [13] [14].
2.3. A Hamilton-Jacobi-Bellman System
Given two functions
, consider the Lagrangian density
. (41)
The corresponding Euler-Lagrange equations of motion are
(42)
for
, which are immediately computed:
(43)
so that the equations of motion are
(44)
Now going back to the first B-K equation
(45)
in (26), which we compare with the first equation in (44), we are obviously motivated to think of
as
and to take
. (46)
That is, we choose
. (47)
Then (44) is the system
(48)
where the second equation in (48) is a Hamilton-Jacobi-Bellman (H-J-B) equation, which as remarked in [11] is well-known in the theory of optimal stochastic control for continuous Markov processes [15]. Although this equation was derived by way of a suitable action functional, defined by the integration of
in (41) for choices
,
, another path to it is by way of the first RD equation in (12) divided by r;
(49)
where the bracketed expression here for
was obtained in the first sentence that followed Equation (23). By the definition (22), and the definition of
again,
. (49) is therefore the statement
, (50)
which is the H-J-B equation in (48).
At hand already we have a solution
of the H-J-B system (48), by formulas (27) and (28). (27) gives
, and we can plug the expression for
there into the first formula in (28) to get
(51)
with
given in (31). Again we choose
.
The useful role of the reaction diffusion system (12) has been noted several times in this section. Typically in physics, chemistry, or biology, for example, a more general system of the form
(52)
is encountered, where
are diffusion constants for
and where
are growth and interaction functions. r and s could be concentration functions for two chemicals, or prey and predator functions in a two-species ecological model, for example.
3. Further Remarks on the Case
It was pointed out in Section 2.1 that various formulas presented in this paper (and in the paper [10]) simplify drastically in case
; in general
. Here we find in this case, in particular, a concrete expression for the potential function
(and thus also for the function
) appearing in some of these formulas.
For
,
, by (9) and (10), is a constant function:
. By (11),
,
, and
(53)
by straight-forward differentiation of R. By Maple, for example, the differentiation of
on the r.h.s. of (53) can be carried out. For
given by (10) and
, the result is that this r.h.s. is
, or
by (29). As we have chosen
in (1) to be
, we see that the second fluid equation in (4) therefore gives
(54)
since
by (10), for
. That is,
is the constant function
, or
, (55)
for a function of integration
. Using again that
, we see that
, for some constant
. Thus, in the end, for
we can choose the potential function
and the associated function
in (13) to be given by
(56)
for a constant
.
These expressions for
and
can be plugged into formulas (14), (15), and (51), for example—taking
there, to further explicate the solutions
; keep in mind the assumption
:
(57)
for
given in (56). We also have the formulas for
and
in (35) in case
. In (57),
, by (13).
Some concluding remarks about the case
pertain to the conservation laws (16) and (17). These laws imply that rs and
are conserved quantities that give rise to constants of motion
(58)
In [16], for example, where
(and
), the mass
and energy
constants, in particular, are computed, where the notation
there (as in [5] [6] [11]) corresponds to
here; also
there corresponds to
in (13) here. We state the results in terms of our notation, but we also express M and E in terms of the Gurevich-Krylov solution
in (10). First note that by (10), (29), (33),(36)
(59)
for
. Then by (18), (22), (27), (59)
,
(60)
The result is that
(61)
using that
(62)
where the latter integral formula in (62) is used to compute the integration of
in the definition of E. Namely, as we have just noted,
so by (36) again
. (63)
4. Plasma Metric and Plasma Dilaton Fields
An exact connection of the cold plasma system (5) to a two-dimensional Jackiw-Teitelboim (J-T) black hole was investigated in [10], with the resonance NLS Equation (1) serving as a bridge. An explicit change of variables was set up which transformed a plasma metric associated with the system (5) to a J-T metric. This transformation, moreover, provided for a direct calculation of a plasma dilaton field, which with the plasma metric and an appropriate cosmological constant constitutes a solution of the J-T gravitational field equations [17] [18]. The results of [10] represent an extension to the non-trivial case
of results in [12] —a case discussed in Sections 2 and 3 here. As indicated in the introduction, two more plasma dilaton fields will be computed in this section, to obtain a set of three linearly independent ones altogether.
The J-T gravitational field equations are a system of equations
(64)
of which a solution consists of a triple
where g is a pseudo Riemannian metric with local components
,
is its Ricci scalar curvature,
is a real-valued function of the local coordinates
in which g is expressed (called a dilaton field),
is a cosmological constant (and therefore the scalar curvature is a constant), and where, locally, the Hessian 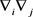 is given by
is given by
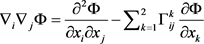 (65)
(65)
for the Christoffel symbols 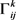 of g, of the second kind.
of g, of the second kind.
For example, the J-T (Lorentzian) black hole solution of the system (64) is given in the coordinates 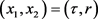 by
by 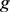 with
with
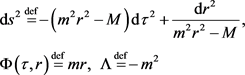 (66)
(66)
for fixed real numbers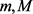 ,
, 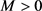 being a black hole mass parameter. Here
being a black hole mass parameter. Here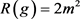 , and we point out that the sign convention for scalar curvature that we adopt here (and in [10] [12]) is spelled out on page 182 of [19], for example. Thus, for example, our
, and we point out that the sign convention for scalar curvature that we adopt here (and in [10] [12]) is spelled out on page 182 of [19], for example. Thus, for example, our 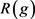 is the negative of that employed in [17] [18]. We will also write
is the negative of that employed in [17] [18]. We will also write 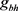 for the J-T metric given in (66).
for the J-T metric given in (66).
As a second example, we consider the plasma metric 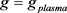 constructed in [10] by way of the G-K solution in (10) of the MAS (5). Here the local coordinates
constructed in [10] by way of the G-K solution in (10) of the MAS (5). Here the local coordinates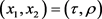 , with the notation
, with the notation 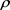 here not to be confused with the same notation for the solution
here not to be confused with the same notation for the solution 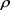 in (10):
in (10):
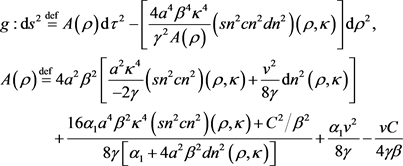 (67)
(67)
where (again) C is given (9). Obviously this metric is more complicated in structure. For  (so that again
(so that again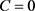 ) and for the choice
) and for the choice ![]() (as in [5] [6]) it reduces to the metric (6) in [12], where the notation b there corresponds to
(as in [5] [6]) it reduces to the metric (6) in [12], where the notation b there corresponds to ![]() here. Some remarks herewith are offered to provide some clarification regarding the “raisons d’être” of the plasma metric formula (67).
here. Some remarks herewith are offered to provide some clarification regarding the “raisons d’être” of the plasma metric formula (67).
The classical continuous Heisenberg model realized on a single sheeted hyperboloid
![]() (68)
(68)
with equations of motion
![]() (69)
(69)
is equipped with a canonical metric
![]() (70)
(70)
of constant scalar curvature![]() . The bracket in (69) is just the commutator
. The bracket in (69) is just the commutator ![]() of two matrices
of two matrices ![]() and
and![]() , and the
, and the ![]() in (70) are simply Minkowski inner product expressions:
in (70) are simply Minkowski inner product expressions: ![]() for
for![]() ,
,![]() .
.
On the other hand, one can construct Lax pairs ![]() for this Heisenberg model, and Lax pairs
for this Heisenberg model, and Lax pairs ![]() for the reaction diffusion system (12), and establish a gauge equivalence of these two nonlinear systems [16]. More precisely, in our specific setup,
for the reaction diffusion system (12), and establish a gauge equivalence of these two nonlinear systems [16]. More precisely, in our specific setup,
![]() (71)
(71)
for a (complex) spectral parameter![]() . The equations of motion assertion (69) is equivalent to the assertion that
. The equations of motion assertion (69) is equivalent to the assertion that ![]() satisfies the zero curvature condition (zcc)
satisfies the zero curvature condition (zcc)
![]() (72)
(72)
Similarly, a pair of functions ![]() is a solution of the RDS (12) if and only if
is a solution of the RDS (12) if and only if ![]() satisfies the zcc
satisfies the zcc
![]() (73)
(73)
Gauge equivalence means that for some![]() ,
,
![]() (74)
(74)
which in turn means that one can show that the Heisenberg metric ![]() in (70) can be expressed in terms of r and s. The result (a key result) is that
in (70) can be expressed in terms of r and s. The result (a key result) is that
![]() (75)
(75)
Since the scalar curvature ![]() of
of ![]() has the value 2, as we have noted, it is convenient to work with the metric
has the value 2, as we have noted, it is convenient to work with the metric ![]() with scalar curvature
with scalar curvature![]() . Now
. Now ![]() by definition (18), so by (27)
by definition (18), so by (27)
![]() . (76)
. (76)
By formulas (34) then
![]() , (77)
, (77)
and by definition (22), ![]() by (77). That is, by (75), (76)
by (77). That is, by (75), (76)
![]() . (78)
. (78)
The computation of ![]() (by (75)) is more involved. By (18) and (22) again,
(by (75)) is more involved. By (18) and (22) again, ![]() , which can be computed by (27) and (34) again. The end result is that
, which can be computed by (27) and (34) again. The end result is that
![]() (79)
(79)
In the very specialized case of![]() ,
, ![]() is given exactly by Equation (63). Formulas (76), (78), (79) (for C given in (9)), which give the structure of the metric
is given exactly by Equation (63). Formulas (76), (78), (79) (for C given in (9)), which give the structure of the metric ![]() were also obtained in [10], by a different method. This metric is non-diagonal:
were also obtained in [10], by a different method. This metric is non-diagonal:![]() . In Section 3 of [10] a suitable change of variables was constructed by which
. In Section 3 of [10] a suitable change of variables was constructed by which ![]() was transformed exactly to the plasma metric g in (67), which is diagonal. For this,
was transformed exactly to the plasma metric g in (67), which is diagonal. For this, ![]() is required to be sufficiently large:
is required to be sufficiently large:
![]() and
and ![]() for
for![]() , (80)
, (80)
with the single condition
![]() for
for![]() . (81)
. (81)
A clarification regarding how the plasma metric ![]() in (67) arises is now established. Also
in (67) arises is now established. Also![]() , as we have seen.
, as we have seen.
We move on now to the main result in [10], which will allow, in particular, for a direct computation of plasma dilaton fields and thus for solutions of the field Equations (64). That main result states that the change of variables ![]() for
for
![]() (82)
(82)
transforms the cold plasma metric ![]() in (67) precisely to the J-T black hole metric
in (67) precisely to the J-T black hole metric ![]() in (66), for m and M there given by
in (66), for m and M there given by
![]() (83)
(83)
Another (more compact) expression is given in (99) for the black hole mass parameter M here, which is indeed positive for
![]() , (84)
, (84)
which we assume. Of course the second condition (84) is automatic for ![]() and the first condition, in fact the condition
and the first condition, in fact the condition![]() , implies the first condition
, implies the first condition ![]() in (80).
in (80).
Going back to the earlier equations ![]() and
and![]() , we conclude from the equality of these scalar curvatures that m must be given by (83), and moreover that by the first field equation in (64) the cosmological constant
, we conclude from the equality of these scalar curvatures that m must be given by (83), and moreover that by the first field equation in (64) the cosmological constant ![]() must be given by
must be given by
![]() . (85)
. (85)
![]() throughout this paper, and we see that the cosmological constant is negative. The dilaton field
throughout this paper, and we see that the cosmological constant is negative. The dilaton field ![]() for the second set of equations in (64), for the plasma metric, can be derived immediately from the J-T dilaton field
for the second set of equations in (64), for the plasma metric, can be derived immediately from the J-T dilaton field ![]() in (66):
in (66):
![]() (86)
(86)
as in [10]. There are, however, two other J-T dilaton fields![]() , that are also solutions of the second set of equations in (64) for the metric
, that are also solutions of the second set of equations in (64) for the metric![]() , and therefore by way of the transformation
, and therefore by way of the transformation ![]() in (82) there are in addition plasma dilaton fields
in (82) there are in addition plasma dilaton fields![]() , for the plasma metric which were not computed in [10], which we compute here.
, for the plasma metric which were not computed in [10], which we compute here.
In fact, one can take
![]() (87)
(87)
so that (as in (86))
![]() (88)
(88)
which means that we need to find expressions for ![]() and
and![]() , given the definitions (82), (83). For convenience, write for now
, given the definitions (82), (83). For convenience, write for now ![]() for
for![]() . Let
. Let
![]() (89)
(89)
Then, as is easily checked, w has factorization ![]() for
for
![]() , (90)
, (90)
which, in turn, can be written as
![]() . (91)
. (91)
The argument in [12], for example, leading up to Equation (55) there verifies this assertion. Therefore
![]() . (92)
. (92)
On the other hand, given the definitions (82), (83), one has by Maple, for example, that
![]() (93)
(93)
for C (as usual) in (9). Using that ![]() and
and ![]() (by (29)), one can write
(by (29)), one can write![]() . In the end,
. In the end,
![]() (94)
(94)
for
![]() (95)
(95)
Next, note that in (83)
![]() (96)
(96)
for the same constant A in definition (11) of [12]:
![]() . (97)
. (97)
Also in (83)
![]() (98)
(98)
It follows that M can also be expressed as
![]() , (99)
, (99)
where![]() . Then
. Then
![]() (100)
(100)
for C and A in (95) and (97), respectfully. In summary, the formulas for ![]() and
and ![]() in (94) and (100) provide for the computation of the plasma dilaton fields
in (94) and (100) provide for the computation of the plasma dilaton fields![]() , in (88) for the plasma metric
, in (88) for the plasma metric ![]() in (67).
in (67).
As usual, all formulas simplify considerably in case![]() :
:
![]() (101)
(101)
by (94), (95), (97), and (100), which gives
![]() (102)
(102)
Apart from the constant factors ![]() and
and![]() , the dilaton fields in (102) (obtained for
, the dilaton fields in (102) (obtained for![]() ) are exactly the ones computed in [12], by a different method; see Equation (10) and Equation (11) there.
) are exactly the ones computed in [12], by a different method; see Equation (10) and Equation (11) there.
5. A Plane Wave Solution of the Magnetoacoustic System
The traveling wave solution ![]() in (10) of the magnetoacoustic system (5) has been of central interest, of course. Equation (15), with
in (10) of the magnetoacoustic system (5) has been of central interest, of course. Equation (15), with ![]() as in (11), relates this solution to the solution
as in (11), relates this solution to the solution ![]() of the resonance NLS equation (1). There is another instance, or another sense, in which solutions of (5) and (1) are related, of which some brief remarks are added in this section.
of the resonance NLS equation (1). There is another instance, or another sense, in which solutions of (5) and (1) are related, of which some brief remarks are added in this section.
The bond between the system (5) and Equation (1) is illustrated further in [20], for example, where it is shown that they share a dispersion relation. More precisely, in place of the traveling wave solution ![]() in (10), consider a plane wave solution
in (10), consider a plane wave solution ![]() of (5) of the form
of (5) of the form
![]() (103)
(103)
for constants![]() , wave frequency
, wave frequency![]() , and wave number k. A proof of the dispersion relation
, and wave number k. A proof of the dispersion relation
![]() (104)
(104)
for the system (5) is given in [20]. There it is also shown that this dispersion relation coincides exactly with the dispersion relation for the RNLS Equation (1), for a linearization of the latter equation about the ground state (condensate) solution
![]() (105)
(105)
of it, for the choice![]() . The dispersion relation for Equation (1) is stated (without proof) in [6], for
. The dispersion relation for Equation (1) is stated (without proof) in [6], for![]() .
.
6. Conclusions
The focal points of interest of this paper have been the nonlinear system (5), which describes the propagation of magnetoacoustic waves in a cold plasma in the presence of a transverse magnetic field, the particular traveling wave solution ![]() of this system given by Gurevich-Krylov in (10), and the construction of new solutions of other nonlinear systems—elliptic function solutions that we have in fact expressed in terms of the solution
of this system given by Gurevich-Krylov in (10), and the construction of new solutions of other nonlinear systems—elliptic function solutions that we have in fact expressed in terms of the solution![]() . These other nonlinear systems considered were that of a Madelung fluid, a reaction diffusion system (which played a distinct, unifying role throughout the paper), systems of Broer-Kaup, Boussinesq, Hamilton-Jacobi-Bellman, and the Jackiw-Teitelboim system of gravitational field equations. An elliptic function solution of the resonance nonlinear Schrödinger Equation (1) is also expressed in terms of the solution
. These other nonlinear systems considered were that of a Madelung fluid, a reaction diffusion system (which played a distinct, unifying role throughout the paper), systems of Broer-Kaup, Boussinesq, Hamilton-Jacobi-Bellman, and the Jackiw-Teitelboim system of gravitational field equations. An elliptic function solution of the resonance nonlinear Schrödinger Equation (1) is also expressed in terms of the solution ![]() in Equation (11) and Equation (15).
in Equation (11) and Equation (15).
Regarding the gravitational field equations (see (64)), in particular, some black hole solutions (![]() ) were presented where
) were presented where ![]() is a pseudo-Riemannian metric (given in (67)) of constant Ricci scalar curvature 4B (
is a pseudo-Riemannian metric (given in (67)) of constant Ricci scalar curvature 4B (![]() for
for ![]() and
and ![]() in (1) and (5)), the
in (1) and (5)), the ![]() are dilaton fields (given by (86), (88), (94), (100), (102)), and
are dilaton fields (given by (86), (88), (94), (100), (102)), and ![]() is a (negative) cosmological constant. To obtain these solutions we used a fundamental result in [10] where an explicit change of variables was set up (which is given in definition (82) here) that transforms
is a (negative) cosmological constant. To obtain these solutions we used a fundamental result in [10] where an explicit change of variables was set up (which is given in definition (82) here) that transforms ![]() precisely to the Jackiw-Teitelboim black hole metric
precisely to the Jackiw-Teitelboim black hole metric ![]() in (66), for the values of m and M there given in (83).
in (66), for the values of m and M there given in (83).
Brief remarks in Section 5 further narrate a nexus between the magnetoacoustic system (5) and the resonance NLS Equation (1)—this by way of the dispersion relation (104).
The results presented here, generally speaking, provide for a non-trivial extension of a few selected results obtained in [11] [12], for example. On the other hand, as pointed out in Section 3, we have not considered an extension in the direction of two-soliton solutions of Broer-Kaup and Boussinesq systems, for example, as discussed in [11]; also see [5] [6] [16].
Acknowledgements
This paper, like that of reference [10], has drawn inspiration from the work of the authors in the references [5] [7], and [21].