Vortex Solitons for a Class of Schrödinger Equation with Square Root Nonlinear Term ()
1. Introduction
In optics research, a fundamental prototype situation is that the light waves are described by a complex-valued wave function governed by nonlinear Schrödinger equations [1] - [8]. These rigorous mathematical treatments of such nonlinear problems provide more possibilities for the existence and properties of optical vortices. Our interest is motivated by the work of Lin, Belić, Petrović, Hajaiej and Chen [9], the mathematical analysis of Lin and Ren [10].
In dimensionless form, consider the following nonlinear Schrödinger equation,
(1)
where E is the evolution of the slowly varing electric field envelope propagating in the longitudinal z-direction;
is the Laplace operator over the transverse plane of coordinates
which is perpendicular to the z-axis. The function f depends on the total field intensity, I, i.e.
, and we will concentrate henceforth on the model of the self-focusing square-root nonlinearity.
(2)
which describes narrow-gap semiconductors [11] [12].
We focus on spatial optical solitons. Spatially localized solutions of (1), which do not change their intensity profile during propagation, can be described under the spatial soliton ansatz
(3)
where r and
are real polar coordinates over
, and
,
,
is the radial profile function which gives rise to the intensity of light waves,
is the winding number, and
is the wave propagation constant. This ansatz describe a vortex wave centered around the z-axis. Inserting (3) into (1) and in a square root nonlinear media, we arrive at the following equation
(4)
Due to the presence of the vortex core, in other words, the regularity of u at
, we impose the condition
. Besides, such ring-like beams remain localized that allows us to mathematically impose the “boundary” condition
for
sufficiently large, where R represents the distance from the vortex core.
Therefore, in view of (4), we can get the n-vortex equation with boundary conditions.
(5)
In this paper, we treat (5) as a nonlinear eigenvalue problem and prove the existence of positive solution pairs
by a constrained minimization approach, with a prescribed energy flux constrained.
2. Preliminary Setting and Main Theorems
In this section, we give some basic notations and lemmas which will be used in next section. In order to approach the Equation (5), we write down the action functional
defined as
(6)
where
, H is the completion of
(7)
equipped with the inner product
(8)
As a Hilbert space, H may be considered as an embedded subspace of
which is composed of radially symmetric functions such that any element
enjoys the desired property
, where
.
Lemma 2.1. From the inequalities
(9)
and
(10)
we get that there exists a constant
, such that
.
For convenience, we define the “energy” functional as
(11)
Now, we state our main theorem in this paper.
Theorem 2.2. For any parameters
, consider the n-vortex Equation (5) with boundary conditions, describing ring-profile vortex solitons in a square-root nonlinear media, with the prescribed energy flux
, and
.
1) There exists a solution pair
with
,
and
.
2) For
, the energy flux
, and there exists no nontrivial solution, if
.
3. Existence of Vortices via Constrained Minimization
In this section, we consider the wave propagation constant
as a Lagrange multiplier, we prove the existence of solution of the Equation (5) with constrained minimization approach.
We rewrite the n-vortex Equation (5) as
(12)
Define the function I and the soliton energy flux as
Thus, to get a solution of (12), it suffices to show that a solution to the following exists:
(13)
where the nonempty admissible class
is defined by
(14)
with
being defined by (11).
The proof of Theorem 2.2. 1) Using the energy flux
, we have
(15)
Let 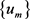 be a minimizing sequence of (13). Then (15) gives the bound
be a minimizing sequence of (13). Then (15) gives the bound
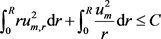 (16)
(16)
where 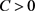 is a constant independent of m. We know the fact that the distributional derivative of u must satisfy
is a constant independent of m. We know the fact that the distributional derivative of u must satisfy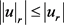 , and the functionals I and
, and the functionals I and 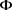 are even. Thus, we may assume that the sequence
are even. Thus, we may assume that the sequence 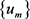 consists of non-negative valued functions. Therefore, it is clear that we may view these functions as radially symmetric over the disk
consists of non-negative valued functions. Therefore, it is clear that we may view these functions as radially symmetric over the disk 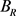 and vanishing on its boundary. Moreover, with (16) and (10), it can be seen that
and vanishing on its boundary. Moreover, with (16) and (10), it can be seen that  belongs in
belongs in 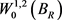 under the reduced norm,
under the reduced norm,
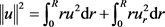 (17)
(17)
Therefore, 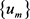 is bounded in
is bounded in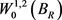 . Without loss of generality, we get the weak convergence of
. Without loss of generality, we get the weak convergence of 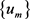 to an element
to an element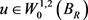 . Using the compact embedding
. Using the compact embedding  for
for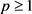 ,
,  strongly in
strongly in 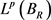 as
as![]() . Hence, u is radially symmetric as well with
. Hence, u is radially symmetric as well with![]() .
.
In view of (16) and Fatou’s lemma, Let ![]() be a measure space and
be a measure space and ![]() a sequence of nonnegative measurable functions. Then the function
a sequence of nonnegative measurable functions. Then the function ![]() is measurable and
is measurable and
![]() (18)
(18)
we have
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Therefore, from (10) and (19)-(21), we get
![]()
Following as in [13]. Let ![]() be a sequence in
be a sequence in ![]() where
where![]() . It is clear that for any
. It is clear that for any![]() ,
, ![]() is bounded in
is bounded in![]() . We may get that
. We may get that ![]() uniformly over
uniformly over ![]() as
as ![]() applying the compact embedding
applying the compact embedding![]() . Thus, we have for any pair
. Thus, we have for any pair![]() , with (16),
, with (16),
![]() (22)
(22)
Taking![]() , we get
, we get
![]() (23)
(23)
Since![]() , the right-hand side of (23) tends to zero as
, the right-hand side of (23) tends to zero as![]() . Hence,
. Hence,
![]()
As a consequence, the boundary condition ![]() is achieved. With (13), u is a solution to (13), and there is a real number
is achieved. With (13), u is a solution to (13), and there is a real number ![]() such that
such that ![]() satisfies (12).
satisfies (12).
Moreover, we may suppose that there is a point ![]() such that
such that![]() , then
, then ![]() since
since ![]() is a minimum point for the function
is a minimum point for the function![]() . By the uniqueness theorem of the initial value problem of ordinary differential equations, we have
. By the uniqueness theorem of the initial value problem of ordinary differential equations, we have ![]() for all
for all![]() , thus contradicting the fact
, thus contradicting the fact![]() . Hence,
. Hence, ![]() for all
for all![]() .
.
2) We establish
![]() (24)
(24)
Suppose otherwise that (24) is not valid, equivalently, ![]() , then there is a
, then there is a ![]() and
and ![]() so that
so that ![]() for all
for all![]() . However,
. However,
![]() (25)
(25)
which contradicts with![]() . So, (24) is valid. From (24), we can find a sequence
. So, (24) is valid. From (24), we can find a sequence ![]() such that
such that ![]() as
as ![]() and
and
![]() (26)
(26)
Multiplying (5) by u, integrating over![]() , letting
, letting![]() . Appealing to (26), we obtain
. Appealing to (26), we obtain
![]() (27)
(27)
Using![]() , we have that
, we have that
![]() (28)
(28)
We may treat u as a radially symmetric function defined over ![]() with its support contained in the disk
with its support contained in the disk![]() . Hence, from the classical
. Hence, from the classical ![]() inequality over
inequality over![]() , we deduce
, we deduce
![]()
with![]() , we have
, we have
![]()
Therefore, when ![]() for
for![]() ,
,![]() . as claimed.
. as claimed.
4. Conclusion
Through the prove of the theorem 2.2, we get that the existence of positive solution pairs ![]() by a constrained minimization approach. In other words, we get the existence of ring-profiled optical vortex solitons propagating in a square-root nonlinear media. Moreover, we obtain that there is no nontrivial small-energy-flux solution satisfying
by a constrained minimization approach. In other words, we get the existence of ring-profiled optical vortex solitons propagating in a square-root nonlinear media. Moreover, we obtain that there is no nontrivial small-energy-flux solution satisfying![]() , if
, if ![]() for
for![]() .
.