Traffic Congestion and Duration Prediction Model Based on Regression Analysis and Survival Analysis

Yidan Liu, Chao Liu, Ziling Zheng

School of Finance, Anhui University of Finance and Economics, Bengbu, China.

DOI: 10.4236/ojbm.2020.82059                

Abstract

With the current situation of traffic congestion becoming more and more serious, how to accurately predict the time of traffic congestion has been widely concerned. In this article, we will build two models to better predict traffic congestion time. First, we use methods to collect the data we need, and through the preliminary cleaning, processing, deletion of missing data, combined calculation of data according to indicators and other steps to screen and integrate the data we need. Then, the multivariate linear regression method is used to construct the traffic prediction congestion model for the existing data, and the actual situation of traffic congestion is obtained. Secondly, the non-parametric method Kaplan-Meier model in the survival analysis method is used to obtain the survival function of traffic congestion duration, and the traffic congestion duration model is constructed. The software programming is solved by MATLAB, Stata, SPSS, etc., and the congestion prediction is obtained. The fitting degree between the predicted value and the actual value of the model is above 0.96, which can better quantify the conclusion that the road traffic operation congestion degree and congestion duration model can identify the characteristics of congestion distribution and duration. Finally, the paper evaluates the advantages and disadvantages of the model objectively, and considers the aspects that can be promoted and applied. I hope that this model can contribute to the prediction research of traffic congestion time!

Keywords

Traffic Congestion Time, Multiple Linear Regression, Survival Analysis Method, Traffic Congestion Prediction Model, Traffic Congestion Duration Model

1. Background

1.1. Background Introduction

With the rapid development of the economy and the improvement of living standards, more and more families have the ability to purchase small cars. The number of cars in the city is increasing day by day, but there are no corresponding supporting measures for urban roads. Urban roads are overwhelmed and congested. Or traffic accidents are happening every day, threatening urban traffic safety. In order to reduce the impact of sub-categories on urban traffic, navigation software is particularly important.

GPS is radio navigation and positioning system based on 24 global positioning satellites to provide three-dimensional position, three-dimensional speed and other information around the world. The positioning principle of GPS is: the user receives the signal transmitted by the satellite, obtains the distance between the satellite and the user, the clock correction and the atmospheric correction, and determines the position of the user through data processing. Now, the positioning accuracy of civilian GPS can reach 10 m or less. The special function of GPS has long attracted the attention of the automotive industry. When the United States announced the opening of a part of GPS system after the Gulf War, the automobile industry immediately seized this opportunity. Investing in the development of car navigation systems, and quickly put into use.

In navigation software, the estimation of travel time is often a function that is important for people’s driving. Existing navigation software often obtains real-time GPS data to determine current road conditions by installing software taxis or vehicles. However, in the case of severe traffic congestion, the speed of the vehicle is slow, and the GPS estimation of the vehicle speed is very inaccurate. This will result in accurate prediction of the vehicle’s travel time by the navigation software, thus affecting the customer’s use and even the operation of the traffic. This paper models and discusses this issue and establishes a more accurate model to predict traffic congestion time.

1.2. Reasons for the Research

First of all, the navigation system’s prediction of the owner’s driving time is not accurate, which will bring the owner a wrong time illusion deviation, which leads to the deviation of the owner’s schedule, which is not conducive to personal life, resulting in poor user experience and loss of trust in navigation software. That will reduce the use of navigation system software and affect the development of navigation software.

Secondly, the navigation system is inaccurate in predicting the travel time of the driving route, which leads to the lack of road conditions in the driving time, and the situation of the road section leading to congestion is worse, greatly reducing the navigation system’s promotion effect on traffic driving, which is not conducive to urban traffic. Improvement has affected social order.

2. Summary of Research

Literature [1] Wang Yuying et al., the factors affecting traffic congestion and the evaluation model, the ratio of average travel time to free-flow travel time, the ratio of travel time and free-flow time to ensure 95% on time, delay, congestion time The Beijing congestion indicator system is constructed in five aspects of the number of congested road sections.

Literature [2] Chen Jian et al. based on the problem of unbalanced travel time demand for public transportation; a two-way planning model was used to construct a bus time differential pricing model. The study pointed out that the implementation of peak increase in fares and flat peaks to reduce fares can help ease traffic pressure.

Literature [3] Zhou Yingxue et al. constructed a risk-based traffic congestion duration model. Taking Beijing traffic as an example, the traffic congestion duration characteristics of working days and weekends, morning peaks and late peaks were analyzed.

Literature [4] [5] [6] driven by “Internet 10” and big data, technologies such as big data and cloud computing are becoming effective ways to solve traffic congestion. Wibisono et al. (2016) visualized traffic big data and predicted traffic flow using the fast incremental tree fern detection model. Kersys (2015) studied the impact of travel time, travel demand change and traffic flow on traffic congestion evaluation.

Based on the above analysis, most of the research on traffic congestion time focuses on time difference pricing, congestion time characteristics, congestion evaluation model, etc., research on the characteristic distribution of congestion duration is less, and then the prediction of traffic congestion time is not quasi. All in all, the existing literature has more or less its deficiencies and needs to be improved.

3. Model Assumption

First, assume that the road surface conditions are the same and the road surface is in good condition.

Second, assume that the roads in the city are in good condition, and there is no control over traffic and occupation of traffic.

Third, it is assumed that the influence of pedestrian traffic flow and bicycle traffic around the road on traffic can be neglected.

Fourth, assume that the driver strictly abides by the traffic rules during the driving process, and there is no violation of traffic regulations such as red lights.

4. Explanation and Symbol Description

4.1. Noun Explanation

1) Average driving speed

The average driving speed refers to the average value of driving speed of all motor vehicles in the same time and the same distance, in km/h. The calculation formula is as follows:

$\bar{v}=\left(L\times N_1\right)/{\displaystyle {\sum }_{i=1}^N{t}_i}$ (1)

where: indicates the average driving speed, km/h; L indicates the driving distance, km; indicates the number of vehicles passing through each hour; indicates the time required for the first vehicle to travel.

2) Average driving time

The average driving time refers to the average time value of all motor vehicles used in the unit distance. The average driving time is negatively correlated with the traffic congestion degree. The formula is as follows:

$\bar{t}=\left(L\times N_1\right)/{\displaystyle {\sum }_{i=1}^N{v}_i}$ (2)

where: is the average driving time, h; L indicates the driving distance, km; indicates the number of vehicles passing every hour; indicates the speed of the first car.

3) Average loss time

The average loss time refers to the time lost by the vehicle due to certain external factors (such as bad weather, traffic accidents, etc.) within a certain unit of travel. This indicator can reflect the smooth flow of traffic and the queuing situation. The calculation formula is as follows:

$T_l=\frac{L}{V_t}-\frac{L}{V_n}$ (3)

where: is the average loss time, h; represents the actual speed of the vehicle, indicates the speed of the motor vehicle in the non-congested state, km/h.

4) Traffic density

Traffic density, also known as traffic flow density, refers to the number of vehicles in a lane over a certain distance. This indicator can reflect the intensity of vehicles on a road. Its calculation formula is as follows:

$TD=\frac{N_2}{L}$ (4)

where: TD indicates the traffic density, vehicle/km; indicates the number of vehicles in a certain moment in the lane; L indicates the driving distance.

5) Traffic volume

Vehicle traffic refers to the number of vehicles passing through a certain road over a period of time. Its calculation formula is as follows:

$TV=\frac{N_3}{t^{*}}$ (5)

where: TV represents the traffic volume, vehicle/h; indicates the number of vehicles passing the road; indicates the observation time.

6) Morning and evening peak

Affected by the commute time, the most congested time of day will be concentrated in the peak of work and the peak hours of work. This paper assumes that the morning peak hours are from 7:30 to 9:30 and the evening peak hours are from 16:30 to 18:30.

7) The number of weeks

In this paper, the number of weeks is divided into two types: weekdays and weekends. Due to different travel purposes, different traffic congestion distribution characteristics will be presented on weekdays and weekends.

8) Traffic congestion index

The traffic congestion index refers to the ratio of excess time to the original time to measure traffic congestion in an area. The traffic index value is expressed by a value between 0 and 10. The larger the value, the more congested the road traffic. The smaller the value, the smoother the traffic, as shown in Table 1 and Table 2.

Table 1. Traffic congestion index rating chart.

4.2. Symbol Description

Table 2. Description of symbols.

5. Models

5.1. Analysis and Solution of Problem One

This question requires us to select appropriate traffic congestion indicators and collect a large number of traffic data sets and process the data. According to the selection of traffic congestion indicators, based on a large number of relevant research data and our understanding of the causes of traffic congestion, we comprehensively analyzed the following seven indicators as factors affecting traffic congestion: average driving speed, average driving time, average Loss time, traffic density, traffic flow, morning and evening peaks, and the number of weeks. And use the traffic congestion index as an indicator to measure the degree of traffic congestion as the explanatory variable of this regression prediction model. The seven indicators we selected are used as explanatory variables, and the morning and evening peaks and the number of weeks are dummy variables.

For data collection and processing, we used various channels to obtain GPS.

Trajectory data for 10,357 vehicles from February 2 to February 8, 2008. The total number of points in the data set is about 15 million, and the total distance of the trajectory reaches 9 million kilometers. We first perform preliminary cleaning, processing, and deletion of missing values. Using the relevant software to represent the trajectory data in the data set on the map, and knows the trajectory range of the data set, as shown in Figure 1.

The selected research range is 121.4358 - 121.5083 and the latitude is 31.2478 - 31.2043, as shown in Figure 2 (in order to make the research range clear, we have enlarged the trajectory data map). It includes sections such as Chengdu North Road, Yan’an East Road and Yan’an East Road Overpass. This range of motor vehicles is highly intensive and most vehicles pass through the area, indicating a typical area where traffic congestion is likely to occur. Therefore, this paper will observe the data information of the vehicles in the road section within the range and use this information to study traffic congestion, as shown in Figure 2.

The data in the processed range is combined and calculated according to the traffic congestion index, time attribute, and related traffic congestion indicators.

Figure 1. Data set trajectory range graph.

Figure 2. Picture of research scope.

First of all, the GPS trajectory data is converted into two-dimensional coordinate data. We convert the latitude and longitude in a large amount of GPS data into geodetic coordinates through relevant software, and then add time factors to make the data into panel data. Finally, the passing time, the relevant coordinate changes, the actual road segment conditions and the calculation formula of the relevant traffic congestion indicators (see §4 noun explanation and symbol description), the traffic congestion index, average driving speed, average driving time, average loss time, car Indicator values such as traffic. Finally, 5913 data were obtained for modeling, forecasting, and traffic congestion duration studies.

5.2. Analysis and Solution of Problem Two

5.2.1. Analysis of the Problem

This problem requires us to make a multiple logarithmic linear regression traffic congestion prediction model and a traffic congestion duration model, so as to improve the accuracy and real-time of traffic congestion prediction by using the model, and estimate the traffic congestion time by using the traffic congestion duration model. Aiming at this problem, we solve it in two steps.

5.2.2. Model Preparation

Traffic congestion index has many influencing factors, including average driving speed, average driving time, average lost time, vehicle flow, traffic density, morning and evening peak, and the number of weeks.

There are many ways to calculate the traffic congestion index. In the United States, traffic delay time is mainly used to calculate the severity index of traffic congestion, combined with the actual situation and existing data in China, the algorithm adopted in this paper is based on the road speed calculation of traffic congestion index to calculate, as shown in Figure 3.

5.2.3. Modeling Ideas

Figure 3. Problem graph.

5.2.4. The Foundation of Model

The traffic congestion index is a conceptual index set by some cities to comprehensively reflect the unimpeded or congested road network according to the road traffic conditions, which is equivalent to digitizing the congestion situation. The calculation method of traffic congestion index is based on section speed: traffic congestion index calculation method:

$A_{ij}=\left(\frac{R{S}_{ij}}{C{S}_{ij}}-1\right)\times 100\%$ (6)

Among them, represents the velocity under the condition of free flow in the time of the section. Represents the actual running speed of section i at time j.

Traffic congestion prediction model

The multiple logarithmic linear regression model is used to study the number of dependent variables (explained variables) and multiple independent variables (explained variables), and to predict and control them. If the dependent variable is y and the independent variable is, the multiple logarithm linear regression model can be expressed as:

$\ln \left(\hat{y}\right)=b_0+b_1{x}_1+b_2{x}_2+\cdots +b_m{x}_m+{\epsilon }_i$ (7)

where: $b_0$ is a constant; $b_i$ is partial regression coefficient. When controlling the logarithmic linear influence of other variables on the dependent variable, it represents the degree of logarithmic linear influence of independent variable $x_i$ ( $1,2,3,\cdots ,m$ ) on the dependent variable y. For n groups of observation data $\left(x_1,x_2,\cdots ,x_m,y_i\right)$, $\left(i=1,2,\cdots ,m\right)$, the logarithmic linear regression model can be expressed as:

Its matrix form is: $\ln \left(y\right)=x\beta +\epsilon$, among them,

$y=\left[\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_n\end{array}\right],x=\left[\begin{array}{ccccc}1& x_{11}& x_{12}& \cdots & x_{1m}\\ 1& x_{21}& x_{22}& \cdots & x_{2m}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& x_{n1}& x_{n2}& \cdots & x_{nm}\end{array}\right]$ (8)

$\beta =\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\\ ⋮\\ {\beta }_m\end{array}\right),\epsilon =\left(\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ ⋮\\ {\epsilon }_n\end{array}\right)$ (9)

Let y estimate be $\hat{y}$, then the residual between the observed value and the estimated value is ${\epsilon }_i=y_i-{\hat{y}}_i$, in order to minimize the residual, even if $Q={\displaystyle {\sum }_{i=1}^n{\left(y_i-{\hat{y}}_i\right)}^2}={\epsilon }^{\prime }\epsilon =\left(y-x\hat{\beta }\right)\left(y-x\hat{\beta }\right)$ reaches the minimum, according to the principle of calculus, when the derivative of Q with respect to $\hat{\beta }$ is equal to 0, the solution can be obtained, named:

$\frac{\partial Q}{\partial \beta }=\frac{\partial \left(y-x\beta \right)\left(y-x\hat{\beta }\right)}{\partial \hat{\beta }}=0$ (10)

traffic jam duration model based on survival analysis.

1) Basic concepts of survival analysis

Survival analysis is a kind of statistical analysis method that combines the result of an event with the time it has experienced. To study the relationship between survival time and outcome and many factors. The basic concepts are shown in Table 3.

2) Survival analysis methods

The methods of survival analysis mainly include parametric method,

Table 3. Basic conception.

semi-parametric method and non-parametric method. When the distribution type is unknown, the non-parametric method has a high computational efficiency, as shown in Table 4.

3) Congestion duration model based on survival analysis

Based on the survival analysis method described above and combined with the actual research situation of this paper, the actual situation of traffic congestion is defined as follows:

a) The survival time of traffic jam refers to the duration from the occurrence of traffic jam to the end of traffic jam.

b) Traffic jams deletion data. The data of traffic jam duration has the deletion feature, which means that traffic jam events occur earlier than the beginning time of the study or the congestion continues after the end of the study time, or incomplete data cannot be accurately recorded due to some factors.

c) The traffic jam survival function is s(t). The traffic jam survival function refers to the sample probability distribution of the existence of congestion from the beginning of traffic jam to time t, also known as the cumulative survival function, as shown below:

$F\left(t\right)=P\left(T\le t\right)={\displaystyle {\int }_0^{t}f\left(x\right)\text{d}x}$ (11)

$s\left(t\right)=P\left(T>t\right)={\displaystyle {\int }_t^{\infty }f\left(x\right)\text{d}x}=1-F\left(t\right)$ (12)

where: $F\left(t\right)$ represents the distribution function; P stands for probability; T represents the duration of traffic jam; f(x) is the probability density of T evaluated at time x. When the survival probability is low, the survival curve s(t) is steep, while when the survival probability is high, the survival curve s(t) is flat.

d) Traffic congestion risk function h(t), the risk function refers to the probability of traffic congestion not disappearing after the occurrence of time t, but disappearing within a minimum time $\Delta t$, also known as conditional survival probability, as shown in the following formula:

$h\left(t\right)={\lim }_{\Delta t\to 0}\frac{P\left(t\le T<t+\Delta t|T\ge t\right)}{\Delta t}=\frac{f\left(t\right)}{s\left(t\right)}=-\frac{d}{d_t}s\left(t\right)$ (13)

The cumulative risk function curve is obtained from the integral of the risk function. The higher its position, the higher the probability of ending the traffic

Table 4. Survivable analysis method.

jam event in time.

5.2.5. Model Solving

Multiple logarithmic linear regression traffic prediction model solution

The above variables are assumed to have logarithmic linear correlation, and the multiple logarithmic linear regression traffic congestion prediction model is established as follows:

$\ln \left(Y\right)=b_0+b_1\bar{v}+b_2\bar{t}+b_3{T}_l+b_{4}TD+b_{5}TV+b_6{D}_1+b_7{D}_2+b_8{D}_3+{\epsilon }_i$ (14)

where, $\bar{v}$ represents average driving speed; $\bar{t}$ represents the average driving time; $T_l$ represents the average loss time; TD represents traffic density; TV represents traffic flow; $D_1$ represents morning peak; $D_2$ represents evening peak; $D_3$ represents the number of weeks; Y represents the traffic congestion index; $b_0$ is a constant; ( $i=1,2,3,4,5,6,7,8$ ) is the regression coefficient.

This paper divides the data set into 60% training set and 40% test set. By using Stata software and training set data, the multiple logarithms linear regression traffic congestion prediction model was regressed, and the estimated value matrix of regression coefficient b was obtained:

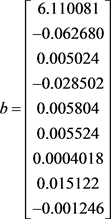
The preliminary multiple logarithm linear regression traffic congestion prediction models are thus obtained:

$\begin{array}{c}\ln \left(y\right)=6.110081-0.062680\bar{v}+0.005024\bar{t}-0.028502T+0.005804TD\\ +0.005524TV+0.0004018D_1+0.015122D_2-0.001246D_3+{\epsilon }_i\end{array}$ (15)

According to the test results, as shown in Table 4 and Table 5, the residual mean square value of the model was only 0.0525, R² was 0.9688, fit degree was 0.969, and the model p < 0.0001. So the regression model is meaningful. Then t test of model regression coefficient, the analysis results can be seen, as shown in Table 6, the regression coefficient P values were less than 0.01, can explain that variable average driving speed, the average loss time, density of traffic, and whether late to peak traffic congestion index to be explained variables influence significantly, and affected by the average driving speed, the largest and P values are greater than 0.50, can be thought of as the average driving time of traffic congestion index had no significant effect, relative to the peak in the morning and evening, and morning rush research sections within the scope of the influence factors is small, It is affected by evening peak, as shown in Tables 5-7.

Table 5. Analysis result.

Table 6. Analysis result.

Table 7. Analysis result.

The model was further analyzed, the insignificant variables were removed, and the regression model was fitted again. Regression diagnosis and model analysis was carried out for the new regression model. According to the analysis results of significance test and fitting degree test, the model had a good fitting effect. Therefore; the city’s multiple logarithms linear regression traffic congestion prediction models is as follows:

$\begin{array}{c}Y=\exp (6.150260-0.0615483\bar{v}-0.032501T_l+0.025061TD\\ +0.032552TV+0.025615D_2-0.002065D_3+{\epsilon }_i)\end{array}$ (16)

5.2.6. Model Prediction

Through the above tests, the traffic congestion model was obtained, and the corresponding predicted value was obtained through the corresponding tests with 40% of the test set, which was compared with the actual value of the traffic congestion index, and the results were shown in Figure 4. Among them, the test set = 0.9734, and the fitting degree was 0.9727, as shown in Figure 4.

In order to further verify the prediction accuracy of the model, the fitting degree of the training set sample and all samples was analyzed in this paper. The fitting effect of the training set sample was shown in the figure, with =0.9688 and fitting degree 0.969. The fitting effect of the total amount of all samples is shown in Figure 5 and Figure 6, with =0.968 and the fitting degree 0.968.

Figure 4. Test set fitting diagram.

Figure 5. Total sample fitting diagram.

Figure 6. Training set fitting diagram.

It can be seen from the figure that the predicted value obtained by the traffic congestion prediction model in this paper has a good fitting result with the actual value. Therefore, it is feasible and effective to use the multiple logarithmic linear regression model proposed in this paper to predict traffic congestion index.

Congestion duration prediction based on survival analysis

Due to traffic congestion duration distribution function is unknown, this paper USES the method of nonparametric Kaplan Meier model for traffic congestion duration of survival function, its principle is: suppose you have n congestion duration samples, duration time period have different k values, making, is traffic congestion duration of survival function s(t) estimate function is as follows:

$s\left(t\right)=\underset{t_j\le t}{{\displaystyle \prod }}\frac{n_j-d_j}{n_j}$

where, n is the number of samples before time, that is, the number of samples that traffic congestion still persists; s(t) is the probability of survival at time.

There is an obvious difference between weekday traffic and weekday traffic in the section studied in this paper. Weekday traffic congestion is significantly more serious and lasts longer than weekday traffic. The morning rush is later than weekday traffic, and the travel rush is near noon. The survival functions of road sections on weekdays and weekends in the research area are shown in Figure 7 and Figure 8.

As can be seen from Figure 9, the survival function of weekdays is above the survival function of weekends, indicating that the frequency of traffic congestion in weekdays is higher than that in weekends, and the duration of traffic congestion

Figure 7. Weekday and weekend survival function graph.

Figure 8. Risk function graph.

Figure 9. Sensitivity analysis diagram.

is longer than that in weekends. At weekends, 87.5% of the traffic jams lasted less than 250 minutes. It is more likely to end the traffic jam within the duration of the traffic jam, and less likely to end the traffic jam beyond the duration of the traffic jam. 87% of the working day traffic jam lasts less than 300 minutes, which means that it is more likely to end the jam within the duration of the traffic jam, while it is less likely to end the traffic jam beyond the duration.

By analyzing the duration of traffic congestion in the three periods of morning peak, afternoon peak and evening peak within the study section, we can see that the duration of traffic congestion in the three periods is quite different, and the duration of traffic congestion in the afternoon peak and evening peak is longer than that in the morning peak. And for the same amount of time, the afternoon rush is less likely to end than the morning rush.

6. Sensitivity Analysis

In question two, we get the survival function calculation formula for the duration of traffic congestion:

$s\left(t\right)={\displaystyle {\prod }_{t_j\le t}\frac{n_j-d_j}{n_j}}$ (17)

where, the number of samples before time $t_j$ and $n_j$, namely, the number of samples that traffic congestion still persists.

The average driving speed and average driving time are regarded as independent variables and the variation range is between [0, 1]. The road capacity is regarded as the dependent variable. The road capacity is taken as the design capacity with the speed of 30 km/h - 40 km/h. For different values, we used MATLAB software programming to conduct sensitivity analysis, and the results were shown in Figure 9.

According to the sensitivity analysis, when there is interference in the average driving speed, the change of the road capacity caused by the change of the equal value is very small. Therefore, the sensitivity analysis has a good effect, that is, the correction coefficient of road congestion has little influence on the capacity of the road.

7. Research Significance

7.1. The Impact on Traffic

Accurate calculation of road capacity and prediction of traffic jam time can help people arrange their travel more reasonably, relieve the degree of urban congestion, and help evacuate the density of vehicles. Improve people’s quality of life, the efficiency of life and even economic activities.

7.2. The Radiative Effect on Social Economy

This model can also learn from the current advanced science and technology and be applied in the field of logistics to predict the arrival time more accurately, so as to help the industries that need to be used in logistics, such as medical refrigeration, fresh fruit and flowers and other industries, and promote economic development and transformation.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	D’Andrea, E. and Marcelloni, F. (2017) Detection of Traffic Congestion and Incidents from GPS Trace Analysis. Expert Systems with Applications, 73, 43-56. https://doi.org/10.1016/j.eswa.2016.12.018
[2]	Yu, X., Xiong, S., He, Y., Wong, W.E. and Zhao, Y. (2016) Research on Campus Traffic Con-Congestion Detection Using BP Neural Network and Markov Model. Journal of Information Security and Applications, 31, 54-60. https://doi.org/10.1016/j.jisa.2016.08.003
[3]	Kong, X., Xu, Z., Shen, G., Wang, J., Yang, Q. and Zhang, B. (2016) Urban Traffic Congestion Estimation and Prediction Based on Floating Car Trajectory Data. Future Generation Computers Systems, 61, 97-107. https://doi.org/10.1016/j.future.2015.11.013
[4]	Bauza, R. and Gozlvez, J. (2013) Traffic Congestion Detection In-Large Scale Scenarios Using Vehicle-to-Vehicle Communications. Journal of Network and Computer Applications, 36, 1295-1307. https://doi.org/10.1016/j.jnca.2012.02.007
[5]	Arturas, K. (2015) Sustainable Urban Transport System Development Reducing Traffic Congestions Costs. Engineering Economics, 22, 5-13.
[6]	Wibisono, A., Jatmiko, W., Wisesa, H.A., Hardjono, B. and Mursanto, P. (2015) Traffic Big Data Prediction and Visualization Using Fast International Model Trees-Drift Detection (FIMT-DD). Knowledge-Based Systems, 93, 33-46. https://doi.org/10.1016/j.jnca.2012.02.007