Using Confidence Statements to Ordering Medians: A Simple Microarray Nonparametric Analysis ()
1. Introduction
This paper proposes an analysis that can be used as an aid for subsequent more complex statistical data analyses, like classification, clustering, logistic regression, etc. For more details see [1]. We discuss ideas to compare two independent groups and to evaluate a measure that indicates which group has smaller (larger) values than the other one. They are simple and effective without the need for sophisticated techniques. This work was motivated by the following example in oncology: preoperative Gleason scores, in general, provide valuable prognoses for cases with prostate cancer. However, this is not verified for patients with a high score of Gleason-7. This group of patients is characterized by tumours displaying considerable morphological heterogeneity among affected regions. Microarray data have been collected to search for a gene set that could distinguish between recurrent (R) and non-recurrent (NR) Gleason-7 prostate cancer patients. A possible important gene that is associated with this disease is the RPS28 gene. In the study, there are two samples: the first sample has  of R patients, and the second sample has
of R patients, and the second sample has 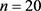 of NR patients. Table 1 lists the microarray expression data for the 25 patients, and an illustration is given in Figure 1. As in many medical experiments, there are only a few cases in this study, and most of them are non-recurrent.
of NR patients. Table 1 lists the microarray expression data for the 25 patients, and an illustration is given in Figure 1. As in many medical experiments, there are only a few cases in this study, and most of them are non-recurrent.
Suppose that the expression of a specific important gene is observed for each patient of the two independent samples, let the recurrent and non-recurrent cases, with inter-ordered samples (observations), be, respectively, 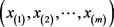 and
and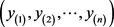 ; m and n are the sample sizes. The objective is to find genes that are under (or over) expressed, which is sometimes expressed by the statement that an expected microarray observation of an R case, x, is smaller (larger) than the expected observation of an NR case, y. In other words, it is conjectured that, for x and y being observations of random variables X and Y, one could expect, for under (over) expressed situations that the probability of
; m and n are the sample sizes. The objective is to find genes that are under (or over) expressed, which is sometimes expressed by the statement that an expected microarray observation of an R case, x, is smaller (larger) than the expected observation of an NR case, y. In other words, it is conjectured that, for x and y being observations of random variables X and Y, one could expect, for under (over) expressed situations that the probability of  is larger (smaller) than a specified value, for example 0.8 (0.2). One of the statistical hypotheses that could indicate the validity of the conjecture is
is larger (smaller) than a specified value, for example 0.8 (0.2). One of the statistical hypotheses that could indicate the validity of the conjecture is 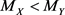 (with M used to indicate median and the subscripts used to separate R and NR cases). Note that uppercase letters are used for random variables and parameters and lowercase letters for observations: probabilities refer to X and Y, and confidence refers to x and y.
(with M used to indicate median and the subscripts used to separate R and NR cases). Note that uppercase letters are used for random variables and parameters and lowercase letters for observations: probabilities refer to X and Y, and confidence refers to x and y.
![]()
Figure 1. RPS28 Arrays for Gleason 7: Non-recurrent and Recurrent Cases.
![]()
Table 1. Expression of Gene RPS28 for Gleason-7 patients: Recurrent and Non-recurrent Cases.
We propose a measure to evaluate the confidence of the statement 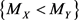 (and obviously of
(and obviously of 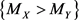 as well). We name this measure as confidence statement. The proposed confidence statement was developed following the ideas of the non-parametric confidence interval for a population’s median based on the binomial distribution. The article is organized as follows: in Section 2, we give a brief review of the confidence interval for the population’s median, and then we introduce the confidence statement; in Section 3, we analyze two real data examples, discussing the applicability of the procedure; and in Section 4, we provide conclusions and final remarks.
as well). We name this measure as confidence statement. The proposed confidence statement was developed following the ideas of the non-parametric confidence interval for a population’s median based on the binomial distribution. The article is organized as follows: in Section 2, we give a brief review of the confidence interval for the population’s median, and then we introduce the confidence statement; in Section 3, we analyze two real data examples, discussing the applicability of the procedure; and in Section 4, we provide conclusions and final remarks.
2. Methods
2.1. Confidence Intervals for Medians
In this section, we present the non-parametric confidence interval for a population’s median based on the binomial distribution. For additional details we refer to [2] [3] [Chap. 7].
An event-related to a random variable X is represented by A, while 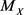 is the median of X.
is the median of X. 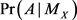 indicates the probability of the event A when
indicates the probability of the event A when 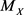 is known. In general, the median
is known. In general, the median 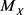 of a random variable X is a population parameter that satisfies the following inequalities:
of a random variable X is a population parameter that satisfies the following inequalities:
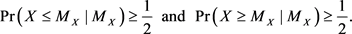 (1)
(1)
In the continuous case, these inequalities are tight:
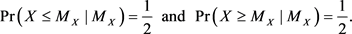 (2)
(2)
Considering that 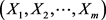 is a vector of m independent and identically distributed random variables, we have that
is a vector of m independent and identically distributed random variables, we have that 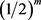 is the probability of the event “all observations are smaller than
is the probability of the event “all observations are smaller than![]() .” Hence, the probability that at least
.” Hence, the probability that at least ![]() (the sample maximum, the parenthesis in the subscript is used to indicate the order) is larger than
(the sample maximum, the parenthesis in the subscript is used to indicate the order) is larger than ![]() is the complementary probability
is the complementary probability![]() . Define
. Define ![]() as the i-th order statistics. One may consider the interval
as the i-th order statistics. One may consider the interval ![]() as a confidence interval for the median
as a confidence interval for the median![]() , for which the value of the confidence is obtained as follows: the probability that all observations are in one of the sides of
, for which the value of the confidence is obtained as follows: the probability that all observations are in one of the sides of![]() , right or left, should be
, right or left, should be![]() . Again, taking the complement, one obtains the probability of the event
. Again, taking the complement, one obtains the probability of the event ![]() as
as![]() .
.
After observing the sample, we write that the statement ![]() has a confidence equal to
has a confidence equal to![]() . We call the attention of the reader to the subtle difference between probability and confidence, as presented in [4], which justifies the use of distinct terminology. To clarify, before the observations are obtained and by using the order statistics
. We call the attention of the reader to the subtle difference between probability and confidence, as presented in [4], which justifies the use of distinct terminology. To clarify, before the observations are obtained and by using the order statistics ![]() and
and ![]() (minimum and maximum), we write the following expression:
(minimum and maximum), we write the following expression:
![]() (3)
(3)
After observing the sample, ![]() is only a statement: we do not know the value of
is only a statement: we do not know the value of ![]() but we know the sample values of all order statistics,
but we know the sample values of all order statistics,![]() . It can be said that one has a confidence of
. It can be said that one has a confidence of ![]() that the median is within the sample extreme values: in this case, there are no probabilities any more. Using the sample of recurrent cases in Table 1, and as
that the median is within the sample extreme values: in this case, there are no probabilities any more. Using the sample of recurrent cases in Table 1, and as![]() , we could say with confidence 93.75% that the interval
, we could say with confidence 93.75% that the interval ![]() contains the population’s median value. Also, as
contains the population’s median value. Also, as ![]() , we are confident that
, we are confident that![]() , with confidence value 96.88%. To be more formal, prior to observations, we use the notation
, with confidence value 96.88%. To be more formal, prior to observations, we use the notation![]() .
.
As an analogy, one can think of the above method as equivalent to tossing a coin m times, computing the probability of zero successes, which is![]() , and taking its complement,
, and taking its complement,![]() . The same arguments can be used to obtain the probability of having two observations in one side and all the remaining on the other side of
. The same arguments can be used to obtain the probability of having two observations in one side and all the remaining on the other side of![]() . The event
. The event ![]() happens if neither
happens if neither ![]() nor
nor ![]() occur. Conditional on
occur. Conditional on ![]() to be known, the probability of
to be known, the probability of ![]() is
is![]() . Hence,
. Hence,![]() . Consequently, the confidence of the interval
. Consequently, the confidence of the interval ![]() is
is![]() . For instance, considering
. For instance, considering![]() , we obtain the confidence values for the statements
, we obtain the confidence values for the statements ![]() and
and![]() , which are equal to 0.96484375 and 0.9296875, respectively. Extending now for any order of statistics, we can think of the number of successes in m tosses of a fair coin.
, which are equal to 0.96484375 and 0.9296875, respectively. Extending now for any order of statistics, we can think of the number of successes in m tosses of a fair coin.
Letting i and j be indices in the set![]() , the events
, the events ![]() and
and ![]() are those in which we are interested. For
are those in which we are interested. For ![]() and by using the same arguments of the previous discussion, we have the following probabilities:
and by using the same arguments of the previous discussion, we have the following probabilities:
![]() (4)
(4)
![]() (5)
(5)
To obtain the confidence of the interval![]() , the same argument of tossing a fair coin is used. We then obtain the following:
, the same argument of tossing a fair coin is used. We then obtain the following:
![]() (6)
(6)
For![]() , we have 0.982421875 and 0.96484375 as the confidence values for the statements
, we have 0.982421875 and 0.96484375 as the confidence values for the statements ![]() and
and![]() , respectively.
, respectively.
To illustrate the confidence interval, we generate a sample with ![]() from a normal distribution with mean 0 and variance 1. The generated data is
from a normal distribution with mean 0 and variance 1. The generated data is
![]() (7)
(7)
We are interested in the interval with 95% of confidence. Our procedure is based in an exact discrete distribution, and it will not obtain an exact 95% standard level (or any other level) but a close one: the higher the sample size, the closer it will be. Our simulated data produce the intervals ![]() and
and ![]() with, respectively, 94.43% and 97.85% of confidence. Since the second, although with smaller amplitude, has larger confidence, we choose it as our confidence interval. From the data, we have that the mean (
with, respectively, 94.43% and 97.85% of confidence. Since the second, although with smaller amplitude, has larger confidence, we choose it as our confidence interval. From the data, we have that the mean (![]() ) is −0.1157 and the standard error (
) is −0.1157 and the standard error (![]() ) is 0.3370, where sd is the standard deviation. Using now the standard method of the confidence interval we obtain the 95.45% confidence interval as
) is 0.3370, where sd is the standard deviation. Using now the standard method of the confidence interval we obtain the 95.45% confidence interval as
![]() (8)
(8)
The length of our 97.85% interval is 0.9698, smaller than 1.3480, which is the length of the standard one based on the t-student distribution, with 95.45% of confidence. Thus, we obtained a more confident shorter interval.
2.2. Confidence Statement on the Order of Medians
Returning to the problem of two samples that are used to compare two sub-populations, assume they are named case and control, the goal is to analyze the statement that the population median ![]() of X is smaller (larger) than the population median
of X is smaller (larger) than the population median ![]() of Y: one of the statements
of Y: one of the statements ![]() or
or ![]() is true. Recall that we use the notation
is true. Recall that we use the notation ![]() and
and ![]() for the ordered sample vectors. In fact, we have independent samples of intra-sample independent and equally distributed observations.
for the ordered sample vectors. In fact, we have independent samples of intra-sample independent and equally distributed observations.
Suppose that there are observations ![]() and
and![]() , such that
, such that![]() . We can write the following probabilities:
. We can write the following probabilities:
![]() (9)
(9)
![]() (10)
(10)
and then for the joint probability one obtains
![]() (11)
(11)
After observing that ![]() for the indices i and j, the confidence of the statement
for the indices i and j, the confidence of the statement ![]() is equal to the right side of the previous expression.
is equal to the right side of the previous expression.
We point out that we are looking for the shortest interval with high confidence. Consequently, to evaluate the confidence of the statement![]() , we should look for the best pair
, we should look for the best pair ![]() such that
such that ![]() that produces a high confidence and a high value of
that produces a high confidence and a high value of![]() . The consequence is that the statement
. The consequence is that the statement ![]() has a confidence equal to
has a confidence equal to
![]() (12)
(12)
The closer we get to 1, the more confident we are about![]() . Note that the probability is evaluated in the sample space of the random variables X and Y, given the constraints of
. Note that the probability is evaluated in the sample space of the random variables X and Y, given the constraints of![]() ,
, ![]() , and
, and![]() , which implies the statement
, which implies the statement![]() . Any probability is a number in the interval
. Any probability is a number in the interval![]() . Values close to 1 have a higher chance to occur. However, we are not evaluating the probability of
. Values close to 1 have a higher chance to occur. However, we are not evaluating the probability of![]() . The result comes from a probability of the sample space, and then instead of having a probability, we have confidence in the statement. This procedure is equal to any confidence interval procedure.
. The result comes from a probability of the sample space, and then instead of having a probability, we have confidence in the statement. This procedure is equal to any confidence interval procedure.
3. Examples
3.1. The Prostate Cancer
In the example shown in Table 1, the statement ![]() has a confidence equal to
has a confidence equal to
![]() (13)
(13)
This is a consequence of the fact that ![]() and that
and that
![]() (14)
(14)
In other words, we are 96.3% confident about the statement![]() .
.
3.2. The Schizophrenia Data Set
The Schizophrenia data set is from the Altar A study of the Stanley Medical Research Institute’s online genomics database (SMRIDB) [5], Higgs 2006 [6]. The data have ![]() patients with schizophrenia and
patients with schizophrenia and ![]() individuals in the control group. 20,993 probe microarrays were reported. Our interest here is to find the most differentially expressed genes. For the analysis, we evaluate both statements
individuals in the control group. 20,993 probe microarrays were reported. Our interest here is to find the most differentially expressed genes. For the analysis, we evaluate both statements ![]() and
and![]() , and keep the highest confidence in each case. Table 2 presents the 10 transcripts with the highest confidence and their respective statements.
, and keep the highest confidence in each case. Table 2 presents the 10 transcripts with the highest confidence and their respective statements.
3.3. Discussion
In the prostate cancer example, it must be noticed that by using the one side t-test one obtains a p-value of 7.24% (14.48% for the two-sided test). This is used to test ![]() versus
versus ![]() (
(![]() for the two-sided test).
for the two-sided test). ![]() here is the notation for the mean, not for medians. Such a particular test has only asymptotic properties if the distributions of X and Y are not normal. On the other hand, the present paper proposes a method that does not use any distribution restriction, is exact and valid for any sample size.
here is the notation for the mean, not for medians. Such a particular test has only asymptotic properties if the distributions of X and Y are not normal. On the other hand, the present paper proposes a method that does not use any distribution restriction, is exact and valid for any sample size.
![]()
Table 2. Schizophrenia data set: genes with the largest confidence.
*MS: median for schizophrenic patients and MC: median for control individuals. Under: For the specific transcript, the schizophrenic group is under expressed in comparison to the control individuals. Over: For the specific transcript, the schizophrenic group is over expressed in comparison to the control individuals.
The development of the present method builds on the studies from [7] [8]. The ideas of conditional statements came from [9]. Simplicity and lack of barriers were our main goals in building such a method. Without restrictions and by being simple, a method might not be able to be powerful. Some non-parametric methods, for example, in Noether 1991 [10], Wasserman 2006 [11], do not directly use all the ordered observations. They only use the order statistics ![]() and
and ![]() of each group.
of each group.
By using the equivalence of confidence statements and significance testing DeGroot 1975 [12], one could, without great distress, state the significance of testing ![]() versus
versus![]() , for the data in Table 1. We are prone to say that the significance favouring
, for the data in Table 1. We are prone to say that the significance favouring ![]() against
against ![]() could be 96.3%. Interchanging the hypotheses but keeping
could be 96.3%. Interchanging the hypotheses but keeping ![]() as the null hypothesis, the exact P-value favouring A would then be 3.7%. That is, under the standard policy, we would reject the hypothesis of equality of medians, and we would expect gene RPS28 to be under-expressed for R patients when compared to the same gene in the NR group.
as the null hypothesis, the exact P-value favouring A would then be 3.7%. That is, under the standard policy, we would reject the hypothesis of equality of medians, and we would expect gene RPS28 to be under-expressed for R patients when compared to the same gene in the NR group.
In the schizophrenia example, we analysed all 20993 genes to find those that were most differentially expressed. We found that among the 10 most differentially expressed transcripts, 4 were under, and 6 were over-expressed. Also, all confidence values were higher than 98%, which are good confidence levels in our opinion.
4. Conclusions
This work intends to provide a method that can be employed as a first-step procedure whenever a data set is to be analyzed. The authors believe that this method can be used to eliminate those variables that have no power to help in the discovery of differentially expressed transcripts, before conducting other more complex/specialized procedures.
The method can be extended to more than two groups. In order to do that, the confidence level to detect a strict order has to be studied in more detail. The larger the number of sample groups, the smaller is the expected confidence. This is because the product of numbers belonging to the interval ![]() clearly produces numbers that are smaller than any of their factors, for instance, consider 3 random variables, X, Y and Z. The following inequality is obvious:
clearly produces numbers that are smaller than any of their factors, for instance, consider 3 random variables, X, Y and Z. The following inequality is obvious:
![]() (15)
(15)
If the observed order of statistics follows the inequality![]() , (for orders a, b, c and d), then the statement
, (for orders a, b, c and d), then the statement ![]() would have smaller confidence than the confidences obtained when comparing a specific pair of the three medians. Hence, the confidence cut-off point to induce decisions would have to decrease with the increasing number of groups that are to be compared.
would have smaller confidence than the confidences obtained when comparing a specific pair of the three medians. Hence, the confidence cut-off point to induce decisions would have to decrease with the increasing number of groups that are to be compared.
de Campos et al. [1] present a general theory that may include the statistical aspects of the present paper. Besides, one can find examples showing the superiority of our method compared with other classical solutions. Marques and Pereira, 2014 [13] can be viewed as a Bayesian non-parametric version of the present paper.
The procedure to evaluate the confidence statement is available in the R package Quor at https://code.google.com/archive/p/quor/. The package is distributed as an open-source program under GPLv3 license.
Acknowledgements
Carlos Alberto de Braganca Pereira is CNPq Fellow-Brazil (308776/2014-3).