Gradient Density Estimation in Arbitrary Finite Dimensions Using the Method of Stationary Phase ()
1. Introduction
Density estimation methods provide a faithful estimate of a non-observable probability density function based on a given collection of observed data [1] [2] [3] [4]. The observed data are treated as random samples obtained from a large population which is assumed to be distributed according to the underlying density function. The aim of our current work is to show that the joint density function of the gradient of a sufficiently smooth function S (density function of
) can be obtained from the normalized power spectrum of
as the free parameter
tends to zero. The proof of this relationship relies on the higher order stationary phase approximation [5] - [10]. The joint density function of the gradient vector field is usually obtained via a random variable transformation, of a uniformly distributed random variable X over the compact domain
, using
as the transformation function. In other words, if we define a random variable
where the random variable X has a uniform distribution on the domain
(
), the density function of Y represents the joint density function of the gradient of S.
In computer vision parlance—a popular application area for density estimation—these gradient density functions are popularly known as the histogram of oriented gradients (HOG) and are primarily employed for human and object detection [11] [12]. The approaches developed in [13] [14] demonstrate an application of HOG—in combination with support vector machines [15] —for detecting pedestrians from infrared images. In a recent article [16], an adaption of the HOG descriptor called the Gradient Field HOG (GF-HOG) is used for sketch-based image retrieval. In these systems, the image intensity is treated as a function
over a 2D domain, and the distribution of intensity gradients or edge directions is used as the feature descriptor to characterize the object appearance or shape within an image. In Section 5 we provide experimental evidence to showcase the efficacy of our method in computing the density of these oriented gradients (HOG). The present work has also been influenced by recent work on quantum supremacy [17] [18] [19]. Here, the aim is to draw samples from the density function of random variables corresponding to the measurement bases of a high-dimensional quantum mechanical wave function. This work may initially seem far removed from our efforts. However, as we will show, the core of our density estimation approach is based on evaluating interval measures of the squared magnitude of a wave function in the frequency domain. For this reason, our approach is deemed a wave function approach to density estimation and henceforth we refer to it as such.
In our earlier effort [20], we primarily focused on exploiting the stationary phase approximation to obtain gradient densities of Euclidean distance functions (R) in two dimensions. As the gradient norm of R is identically equal to 1 almost everywhere, the density of the gradient is one-dimensional and defined over the space of orientations. The key point to be noted here is that the dimensionality of the gradient density (one) is one less than the dimensionality of the space (two) and the constancy of the gradient magnitude of R causes its Hessian to vanish almost everywhere. In Lemma 2.3 below, we see that the Hessian is deeply connected to the density function of the gradient. The degeneracy of the Hessian precluded us from directly employing the stationary phase method and hence techniques like symmetry-breaking had to be used to circumvent the vanishing Hessian problem. The reader may refer to [20] for a more detailed explanation. In contrast to our previous work, we regard our current effort as a generalization of the gradient density estimation result, now established for arbitrary smooth functions in arbitrary finite dimensions.
1.1. Main Contribution
We introduce a new approach for computing the density of Y, where we express the given function S as the phase of a wave function
, specifically
for small values of
, and then consider the normalized power spectrum—squared magnitude of the Fourier transform—of
[21]. We show that the computation of the joint density function of
may be approximated by the power spectrum of
, with the approximation becoming increasingly tight point-wise as
. Using the stationary phase approximation, a well known technique in asymptotic analysis [9], we show that in the limiting case as
, the power spectrum of
converges to the density of Y, and hence can serve as its density estimator at small, non-zero values of
. In other words, if
denotes the density of Y, and if
corresponds to the power spectrum of
at a given value of
, Theorem 3.2 constitutes the following relation,
where
is a small neighborhood around
. We would like to emphasize that our work is fundamentally different from estimating the gradient of a density function [22] and should not be semantically confused with it.
1.2. Significance of Our Result
As mentioned before, the main objective of our current work is to generalize our effort in [20] and demonstrate the fact that the wave function method for obtaining densities can be extended to arbitrary functions in arbitrary finite dimensions. However, one might broach a legitimate question, namely “What is the primary advantage of this approach over other simpler, effective and traditional techniques like histograms which can compute the HOG say by mildly smoothing the image, computing the gradient via (for example) finite differences and then binning the resulting gradients?”. The benefits are three fold:
• One of the foremost advantages of our wave function approach is that it recovers the joint gradient density function of S without explicitly computing its gradient. Since the stationary points capture gradient information and map them into the corresponding frequency bins, we can directly work with S without the need to compute its derivatives.
• The significance of our work is highlighted when we deal with the more practical finite sample-set setting wherein the gradient density is estimated from a finite, discrete set of samples of S rather than assuming the availability of the complete description of S on
. Given the N samples of S on
, it is customary to know the approximation error of a proposed density estimation method as
. In [23] we prove that in one dimension, the point-wise approximation error between our wave function method and the true density is bounded above by
when
. For histograms and kernel density estimators [1] [2], the approximation errors are established for the integrated mean squared error (IMSE) defined as the expected value (with respect to samples of size N) of the square of the
error between the true and the computed probability densities and are shown to be
[24] [25] and
[26] respectively. Having laid the foundation in this work, we plan to invest our future efforts in pursuit of similar upper bounds in arbitrary finite dimensions.
• Furthermore, obtaining the gradient density using our framework in the finite N sample setting is simple, efficient, and computable in
time as elucidated in the last paragraph of Section 4.
1.3. Motivation from Quantum Mechanics
Our wave function method is motivated by the classical-quantum relation, wherein classical physics is expressed as a limiting case of quantum mechanics [27] [28]. When S is treated as the Hamilton-Jacobi scalar field, the gradients of S correspond to the classical momentum of a particle [29]. In the parlance of quantum mechanics, the squared magnitude of the wave function expressed either in its position or momentum basis corresponds to its position or momentum density respectively. Since these representations (either in the position or momentum basis) are simply (suitably scaled) Fourier transforms of each other, the squared magnitude of the Fourier transform of the wave function expressed in its position basis is its quantum momentum density. However, the time independent Schrödinger wave function
(expressed in its position basis) can be approximated by
as
[28]. Here
(treated as a free parameter in our work) represents Planck’s constant. Hence the squared magnitude of the Fourier transform of
corresponds to the quantum momentum density of S. The principal results proved in the article state that the classical momentum density (denoted by P) can be expressed as a limiting case (as
) of its corresponding quantum momentum density (denoted by
), in agreement with the correspondence principle.
2. Existence of Joint Densities of Smooth Function Gradients
We begin with a compact measurable subset
of
on which we consider a smooth function
. We assume that the boundary of
is smooth and the function S is well-behaved on the boundary as elucidated in Appendix B. Let
denote the Hessian of S at a location
and let
denote its determinant. The signature of the Hessian of S at
, defined as the difference between the number of positive and negative eigenvalues of
, is represented by
. In order to exactly determine the set of locations where the joint density of the gradient of S exists, consider the following three sets:
(2.1)
(2.2)
and
(2.3)
Let
. We employ a number of useful lemma, stated here and proved in Appendix A.
Lemma 2.1. [Finiteness Lemma]
is finite for every
.
As we see from Lemma 2.1 above, for a given
, there is only a finite collection of
that maps to
under the function
. The inverse map
which identifies the set of
that maps to
under
is ill-defined as a function as it is a one to many mapping. The objective of the following lemma (Lemma 2.2) is to define appropriate neighborhoods such that the inverse function
, required in the proof of our main Theorem 3.2, when restricted to those neighborhoods is well-defined.
Lemma 2.2. [Neighborhood Lemma] For every
, there exists a closed neighborhood
around
such that
is empty. Furthermore, if
,
can be chosen such that we can find a closed neighborhood
around each
satisfying the following conditions:
1)
.
2)
.
3) The inverse function
is well-defined.
4) For
.
Lemma 2.3 [Density Lemma] Given
, the probability density of
on
is given by
(2.4)
where
and
is the Lebesgue measure.
From Lemma 2.3, it is clear that the existence of the density function P at a location
necessitates a non-vanishing Hessian matrix (
)
. Since we are interested in the case where the density exists almost everywhere on
, we impose the constraint that the set
in (2.2), comprising all points where the Hessian vanishes, has zero Lebesgue measure. It follows that
. Furthermore, the requirement regarding the smoothness of S (
) can be relaxed to functions S in
where d is the dimensionality of
as we will see in Section 3.2.2.
3. Equivalence of the Densities of Gradients and the Power Spectrum
Define the function
as
(3.1)
or
.
is very similar to the Fourier transform of the function
. The normalizing factor in
comes from the following lemma (Lemma 3.1) whose proof is given in Appendix A.
Lemma 3.1. [Integral Lemma ]
and
.
The power spectrum defined as
(3.2)
equals the squared magnitude of the Fourier transform. Note that
. From Lemma (3.1), we see that
. Our fundamental contribution lies in interpreting
as a density function and showing its equivalence to the density function
defined in (2.4). Formally stated:
Theorem 3.2. For
,
where
is a ball around
of radius
.
Before embarking on the proof, we would like to emphasize that the ordering of the limits and the integral as given in the theorem statement is crucial and cannot be arbitrarily interchanged. To press this point home, we show below that after solving for
, the
does not exist. Hence, the order of the integral followed by the limit
cannot be interchanged. Furthermore, when we swap the limits of  and
and , we get
, we get
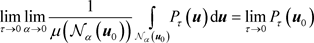
which also does not exist. Hence, the theorem statement is valid only for the specified sequence of limits and the integral.
3.1. Brief Exposition of the Result
To understand the result in simpler terms, let us reconsider the definition of the scaled Fourier transform given in (3.1). The first exponential 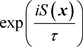 is a varying complex “sinusoid”, whereas the second exponential
is a varying complex “sinusoid”, whereas the second exponential  is a fixed complex sinusoid at frequency
is a fixed complex sinusoid at frequency . When we multiply these two complex exponentials, at low values of
. When we multiply these two complex exponentials, at low values of , the two sinusoids are usually not “in sync” and tend to cancel each other out. However, around the locations where
, the two sinusoids are usually not “in sync” and tend to cancel each other out. However, around the locations where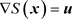 , the two sinusoids are in perfect sync (as the combined exponent is stationary) with the approximate duration of this resonance depending on
, the two sinusoids are in perfect sync (as the combined exponent is stationary) with the approximate duration of this resonance depending on . The value of the integral in (3.1) can be increasingly closely approximated via the stationary phase approximation [9] as
. The value of the integral in (3.1) can be increasingly closely approximated via the stationary phase approximation [9] as
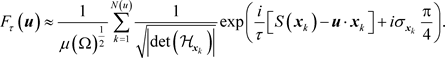
The approximation is increasingly tight as . The power spectrum (
. The power spectrum ( ) gives us the required result
) gives us the required result 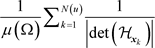 except for the cross phase factors
except for the cross phase factors  obtained as a byproduct of two or more remote locations
obtained as a byproduct of two or more remote locations 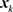 and
and 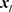 indexing into the same frequency bin
indexing into the same frequency bin , i.e.,
, i.e., 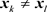 , but
, but![]() . The cross phase factors when evaluated are equivalent to
. The cross phase factors when evaluated are equivalent to![]() , the limit of which does not exist as
, the limit of which does not exist as![]() . However, integrating the power spectrum over a small neighborhood
. However, integrating the power spectrum over a small neighborhood ![]() around
around ![]() removes these cross phase factors as
removes these cross phase factors as ![]() tends to zero and we obtain the desired result.
tends to zero and we obtain the desired result.
3.2. Formal Proof of Theorem 3.2
We wish to compute the integral
![]() (3.3)
(3.3)
at small values of ![]() and exhibit the connection between the power spectrum
and exhibit the connection between the power spectrum ![]() and the density function
and the density function![]() . To this end define
. To this end define ![]() . The proof follows by considering two cases: the first case in which there are no stationary points and therefore the density should go to zero, and the second case in which stationary points exist and the contribution from the oscillatory integral is shown to increasingly closely approximate the density function of the gradient as
. The proof follows by considering two cases: the first case in which there are no stationary points and therefore the density should go to zero, and the second case in which stationary points exist and the contribution from the oscillatory integral is shown to increasingly closely approximate the density function of the gradient as![]() .
.
case (i): We first consider the case where![]() , i.e.,
, i.e.,![]() . In other words there are no stationary points [9] for this value of
. In other words there are no stationary points [9] for this value of![]() . The proof that this case yields the anticipated contribution of zero follows clearly from a straightforward technique commonly used in stationary phase expansions. We assume that the function S is sufficiently well-behaved on the boundary such that the total contribution due to the stationary points of the second kind [9] approaches zero as
. The proof that this case yields the anticipated contribution of zero follows clearly from a straightforward technique commonly used in stationary phase expansions. We assume that the function S is sufficiently well-behaved on the boundary such that the total contribution due to the stationary points of the second kind [9] approaches zero as![]() . (We concentrate here on the crux of our work and reserve the discussion concerning the behavior of S on the boundary and the relationship to stationary points of the second kind to Appendix 8.) Under mild conditions (outlined in Appendix B), the contributions from the stationary points of the third kind can also be ignored as they approach zero as
. (We concentrate here on the crux of our work and reserve the discussion concerning the behavior of S on the boundary and the relationship to stationary points of the second kind to Appendix 8.) Under mild conditions (outlined in Appendix B), the contributions from the stationary points of the third kind can also be ignored as they approach zero as ![]() tends to zero [9]. Higher order terms follow suit.
tends to zero [9]. Higher order terms follow suit.
Lemma 3.3. Fix![]() . If
. If ![]() then
then ![]() as
as![]() .
.
Proof. To improve readability, we prove Lemma 3.3 first in the one dimensional setting and separately offer the proof for multiple dimensions.
3.2.1. Proof of Lemma 3.3 in One Dimension
Let s denote the derivative (1D gradient) of S. The bounded closed interval ![]() is represented by
is represented by![]() , with the length
, with the length![]() . As
. As![]() , there is no
, there is no ![]() for which
for which![]() . Recalling the definition of
. Recalling the definition of![]() , namely
, namely![]() , we see that
, we see that ![]() and is of constant sign in
and is of constant sign in![]() . It follows that
. It follows that ![]() is strictly monotonic. Defining
is strictly monotonic. Defining![]() , we have from (3.1)
, we have from (3.1)
![]()
Here![]() . The inverse function is guaranteed to exist due to the monotonicity of
. The inverse function is guaranteed to exist due to the monotonicity of![]() . Integrating by parts we get
. Integrating by parts we get
![]() (3.4)
(3.4)
It follows that
![]()
3.2.2. Proof of Lemma 3.3 in Finite Dimensions
As![]() , the vector field
, the vector field
![]()
is well-defined. Choose ![]() (with this choice explained below) and for
(with this choice explained below) and for![]() , recursively define the function
, recursively define the function ![]() and the vector field
and the vector field ![]() as follows:
as follows:
![]()
![]()
and
![]()
Using the equality
![]() (3.5)
(3.5)
where ![]() is the divergence operator, and applying the divergence theorem m times, the Fourier transform in (3.3) can be rewritten as
is the divergence operator, and applying the divergence theorem m times, the Fourier transform in (3.3) can be rewritten as
![]() (3.6)
(3.6)
which is similar to (3.4).
We would like to add a note on the differentiability of S which we briefly mentioned after Lemma 2.3. The divergence theorem is applied ![]() times to obtain sufficiently higher order powers of
times to obtain sufficiently higher order powers of ![]() in the numerator so as to exceed the
in the numerator so as to exceed the ![]() term in the denominator of the first line of (3.6). This necessitates that S is at least
term in the denominator of the first line of (3.6). This necessitates that S is at least ![]() times differentiable. The smoothness constraint on S can thus be relaxed and replaced by
times differentiable. The smoothness constraint on S can thus be relaxed and replaced by![]() .
.
The additional complication of the d-dimensional proof lies in resolving the geometry of the terms in the second line of (3.6). Here ![]() is the unit outward normal to the positively oriented boundary
is the unit outward normal to the positively oriented boundary ![]() parameterized by
parameterized by![]() . As
. As![]() , the term on the right side of the first line in (3.6) is
, the term on the right side of the first line in (3.6) is ![]() and hence can be overlooked. To evaluate the remaining integrals within the summation in (3.6), we should take note that the stationary points of the second kind for
and hence can be overlooked. To evaluate the remaining integrals within the summation in (3.6), we should take note that the stationary points of the second kind for ![]() on
on ![]() correspond to the first kind of stationary points for
correspond to the first kind of stationary points for ![]() on the boundary
on the boundary![]() . We show in case (ii) that the contribution of a stationary point of the first kind in a
. We show in case (ii) that the contribution of a stationary point of the first kind in a ![]() dimensional space is
dimensional space is![]() . As the dimension of
. As the dimension of ![]() is
is![]() , we can conclude that the total contribution from the stationary points of the second kind is
, we can conclude that the total contribution from the stationary points of the second kind is![]() . After multiplying and dividing this contribution by the corresponding
. After multiplying and dividing this contribution by the corresponding ![]() and
and ![]() factors respectively, it is easy to see that the contribution of the jth integral (out of the n integrals in the summation) in (3.6) is
factors respectively, it is easy to see that the contribution of the jth integral (out of the n integrals in the summation) in (3.6) is![]() , and hence the total contribution of the m integrals is of
, and hence the total contribution of the m integrals is of![]() . Here, we have safely ignored the stationary points of the third kind as their contributions are minuscule compared to the other two kinds as shown in [9]. Combining all the terms in (3.6) we get the desired result, namely
. Here, we have safely ignored the stationary points of the third kind as their contributions are minuscule compared to the other two kinds as shown in [9]. Combining all the terms in (3.6) we get the desired result, namely![]() . For a detailed exposition of the proof, we encourage the reader to refer to Chapter 9 in [9].
. For a detailed exposition of the proof, we encourage the reader to refer to Chapter 9 in [9].
We then get![]() . Since
. Since ![]() is a compact set in
is a compact set in ![]() and
and![]() , we can choose a neighborhood
, we can choose a neighborhood ![]() around
around ![]() such that for
such that for![]() , no stationary points exist and hence
, no stationary points exist and hence
![]()
Since the cardinality ![]() of the set
of the set ![]() defined in (2.1) is zero for
defined in (2.1) is zero for![]() , the true density
, the true density ![]() of the random variable transformation
of the random variable transformation ![]() given in (2.4) also vanishes for
given in (2.4) also vanishes for![]() .
.
case (ii): For![]() , let
, let![]() . In this case, the number of stationary points in the interior of
. In this case, the number of stationary points in the interior of ![]() is non-zero and finite as a consequence of Lemma 2.1. We can then rewrite
is non-zero and finite as a consequence of Lemma 2.1. We can then rewrite
![]() , (3.7)
, (3.7)
where
![]() (3.8)
(3.8)
and the domain![]() . The closed regions
. The closed regions ![]() are obtained from Lemma 2.2.
are obtained from Lemma 2.2.
Firstly, note that the the set K contains no stationary points by construction. Secondly, the boundaries of K can be classified into two categories: those that overlap with the sets ![]() and those that coincide with
and those that coincide with![]() . Propitiously, the orientation of the overlapping boundaries between the sets K and each
. Propitiously, the orientation of the overlapping boundaries between the sets K and each ![]() are in opposite directions as these sets are located at different sides when viewed from the boundary. Hence, we can exclude the contributions from the overlapping boundaries between K and
are in opposite directions as these sets are located at different sides when viewed from the boundary. Hence, we can exclude the contributions from the overlapping boundaries between K and ![]() while evaluating
while evaluating ![]() in (3.7) as they cancel each other out.
in (3.7) as they cancel each other out.
To compute G we leverage case (i), which also includes the contribution from the boundary![]() , and get
, and get
![]() (3.9)
(3.9)
To evaluate the remaining integrals over![]() , we take into account the contribution from the stationary point at
, we take into account the contribution from the stationary point at ![]() and obtain
and obtain
![]() (3.10)
(3.10)
where
![]() (3.11)
(3.11)
for a continuous bounded function ![]() [9]. The variable a in (3.10) takes the value 1 if
[9]. The variable a in (3.10) takes the value 1 if ![]() lies in the interior of
lies in the interior of![]() , otherwise equals
, otherwise equals ![]() if
if![]() . Since
. Since![]() , stationary points do not occur on the boundary and hence
, stationary points do not occur on the boundary and hence ![]() for our case. Recall that
for our case. Recall that ![]() is the signature of the Hessian at
is the signature of the Hessian at![]() . Note that the main term has the factor
. Note that the main term has the factor ![]() in the numerator, when we perform stationary phase in d dimensions, as mentioned under the finite dimensional proof of Lemma 3.3.
in the numerator, when we perform stationary phase in d dimensions, as mentioned under the finite dimensional proof of Lemma 3.3.
Coupling (3.7), (3.8), and (3.10) yields
![]() (3.12)
(3.12)
where
![]()
As ![]() and
and ![]() from (3.9) and (3.11) respectively, we have
from (3.9) and (3.11) respectively, we have![]() . Based on the definition of the power spectrum
. Based on the definition of the power spectrum ![]() in (3.2), we get
in (3.2), we get
![]() (3.13)
(3.13)
where ![]() includes both the squared magnitude of
includes both the squared magnitude of ![]() and the cross terms involving the first term in (3.12) and
and the cross terms involving the first term in (3.12) and![]() . Notice that the main term in (3.12) can be bounded independently of
. Notice that the main term in (3.12) can be bounded independently of ![]() as
as
![]()
and![]() . Since
. Since![]() , we get
, we get![]() . Furthermore, as
. Furthermore, as ![]() can also be uniformly bounded by a function of
can also be uniformly bounded by a function of ![]() for small values of
for small values of![]() , we have
, we have
![]() (3.14)
(3.14)
Observe that the term on the right side of the first line in (3.13) matches the anticipated expression for the density function ![]() given in (2.4). The cross phase factors in the second line of (3.13 arise due to multiple remote locations
given in (2.4). The cross phase factors in the second line of (3.13 arise due to multiple remote locations ![]() and
and ![]() indexing into
indexing into![]() . The cross phase factors when evaluated can be shown to be proportional to
. The cross phase factors when evaluated can be shown to be proportional to![]() . Since
. Since ![]() is not defined,
is not defined, ![]() does not exist. We briefly alluded to this problem immediately following the statement of Theorem 3.2 in Section 3. However, the following lemma which invokes the inverse function
does not exist. We briefly alluded to this problem immediately following the statement of Theorem 3.2 in Section 3. However, the following lemma which invokes the inverse function![]() —defined in Lemma 2.2 where
—defined in Lemma 2.2 where ![]() is written as a function of
is written as a function of![]() —provides a simple way to nullify the cross phase factors. Note that since each
—provides a simple way to nullify the cross phase factors. Note that since each ![]() is a bijection,
is a bijection, ![]() doesn’t vary over
doesn’t vary over![]() . Pursuant to Lemma 2.2, the Hessian signatures
. Pursuant to Lemma 2.2, the Hessian signatures ![]() and
and ![]() also remain constant over
also remain constant over![]() .
.
Lemma 3.4. [Cross Factor Nullifier Lemma] The integral of the cross term in the second line of (3.13) over the closed region ![]() approaches zero as
approaches zero as![]() , i.e.,
, i.e., ![]()
![]() (3.15)
(3.15)
The proof is given in Appendix A. Combining (3.14) and (3.15) yields
![]() (3.16)
(3.16)
Equation (3.16) demonstrates the equivalence of the cumulative distributions corresponding to the densities ![]() and
and ![]() when integrated over any sufficiently small neighborhood
when integrated over any sufficiently small neighborhood ![]() of radius
of radius![]() . To recover the density
. To recover the density![]() , we let
, we let ![]() and take the limit with respect to
and take the limit with respect to![]() .
.
Taking a mild digression from the main theme of this paper, in the next section (Section 4), we build an informal bridge between the commonly used characteristic function formulation for computing densities and our wave function method. The motivation behind this section is merely to provide an intuitive reason behind our Theorem 3.2, where we directly manipulate the power spectrum of ![]() into the characteristic function formulation stated in (4.2), circumventing the need for the closed-form expression of the density function
into the characteristic function formulation stated in (4.2), circumventing the need for the closed-form expression of the density function ![]() given in (2.4). We request the reader to bear in mind the following cautionary note. What we show below cannot be treated as a formal proof of Theorem 3.2. Our attempt here merely provides a mathematically intuitive justification for establishing the equivalence between the power spectrum and the characteristic function formulations and thereby to the density function
given in (2.4). We request the reader to bear in mind the following cautionary note. What we show below cannot be treated as a formal proof of Theorem 3.2. Our attempt here merely provides a mathematically intuitive justification for establishing the equivalence between the power spectrum and the characteristic function formulations and thereby to the density function![]() . On the basis of the reasons described therein, we strongly believe that the mechanism of stationary phase is essential to formally prove our main theorem (Theorem 3.2). It is best to treat the wave function and the characteristic function methods as two different approaches for estimating the probability density functions and not reformulations of each other. To press this point home, we also comment on the computational complexity of the wave function and the characteristic function methods at the end of the next section.
. On the basis of the reasons described therein, we strongly believe that the mechanism of stationary phase is essential to formally prove our main theorem (Theorem 3.2). It is best to treat the wave function and the characteristic function methods as two different approaches for estimating the probability density functions and not reformulations of each other. To press this point home, we also comment on the computational complexity of the wave function and the characteristic function methods at the end of the next section.
4. Relation between the Characteristic Function and Power Spectrum Formulations of the Gradient Density
The characteristic function ![]() for the random variable
for the random variable ![]() is defined as the expected value of
is defined as the expected value of![]() , namely
, namely
![]() (4.1)
(4.1)
Here ![]() denotes the density of the uniformly distributed random variable X on
denotes the density of the uniformly distributed random variable X on![]() .
.
The inverse Fourier transform of a characteristic function also serves as the density function of the random variable under consideration [30]. In other words, the density function ![]() of the random variable Y can be obtained via
of the random variable Y can be obtained via
![]() (4.2)
(4.2)
Having set the stage, we can now proceed to highlight the close relationship between the characteristic function formulation of the density and our formulation arising from the power spectrum. For simplicity, we choose to consider a region ![]() that is the product of closed intervals,
that is the product of closed intervals,![]() . Based on the expression for the scaled Fourier transform
. Based on the expression for the scaled Fourier transform ![]() in (3.1), the power spectrum
in (3.1), the power spectrum ![]() is given by
is given by
![]()
Define the following change of variables,
![]()
Then ![]() and the integral limits for
and the integral limits for ![]() and
and ![]() are given by
are given by
![]()
![]()
where ![]() is the ith component of
is the ith component of![]() . Note that the Jacobian of this transformation is
. Note that the Jacobian of this transformation is![]() . Now we may write the integral
. Now we may write the integral ![]() in terms of these new variables as
in terms of these new variables as
![]() (4.3)
(4.3)
where
![]() (4.4)
(4.4)
The mean value theorem applied to ![]() yields
yields
![]() (4.5)
(4.5)
where
![]()
with![]() . When
. When ![]() is fixed and
is fixed and![]() ,
, ![]() and so for small values of
and so for small values of ![]() we get
we get
![]() (4.6)
(4.6)
Again we would like to drive the following point home. We do not claim that we have formally proved the above approximation. On the contrary, we believe that it might be an onerous task to do so as the mean value theorem point ![]() in (4.5) is unknown and the integration limits for
in (4.5) is unknown and the integration limits for ![]() directly depend on
directly depend on![]() . The approximation is stated with the sole purpose of providing an intuitive reason for our theorem (Theorem 3.2) and to provide a clear link between the characteristic function and wave function methods for density estimation.
. The approximation is stated with the sole purpose of providing an intuitive reason for our theorem (Theorem 3.2) and to provide a clear link between the characteristic function and wave function methods for density estimation.
Furthermore, note that the integral range for ![]() depends on
depends on ![]() and so when
and so when![]() ,
, ![]() as
as ![]() and hence the above approximation for
and hence the above approximation for
![]() in (4.6) might seem to break down. To evade this seemingly ominous problem, we manipulate the domain of integration for
in (4.6) might seem to break down. To evade this seemingly ominous problem, we manipulate the domain of integration for ![]() as follows. Fix an
as follows. Fix an ![]() and let
and let
![]()
where
![]() (4.7)
(4.7)
By defining ![]() as above, note that in
as above, note that in![]() ,
, ![]() is deliberately made to be
is deliberately made to be ![]() and hence
and hence ![]() as
as![]() . Hence the approximation for
. Hence the approximation for ![]() in (4.6) might hold for this integral range of
in (4.6) might hold for this integral range of![]() . For consideration of
. For consideration of![]() , recall that Theorem 3.2 requires the power spectrum
, recall that Theorem 3.2 requires the power spectrum ![]() to be integrated over a small neighborhood
to be integrated over a small neighborhood ![]() around
around![]() . By using the true expression for
. By using the true expression for ![]() from (4.4) and performing the integral for
from (4.4) and performing the integral for ![]() prior to
prior to ![]() and
and![]() , we get
, we get
![]()
Since both ![]() in (4.7) and the lower and the upper limits for
in (4.7) and the lower and the upper limits for![]() , namely
, namely ![]() respectively approach
respectively approach ![]() as
as![]() , the Riemann-Lebesgue lemma [21] guarantees that
, the Riemann-Lebesgue lemma [21] guarantees that![]() , the integral
, the integral
![]()
approaches zero as![]() . Hence for small values of
. Hence for small values of![]() , we can expect the integral over
, we can expect the integral over ![]() to dominate over the other. This leads to the following approximation,
to dominate over the other. This leads to the following approximation,
![]() (4.8)
(4.8)
as ![]() approaches zero. Combining the above approximation with the approximation for
approaches zero. Combining the above approximation with the approximation for ![]() given in (4.6) and noting that the integral domain for
given in (4.6) and noting that the integral domain for ![]() and
and ![]() approaches
approaches ![]() and
and ![]() respectively as
respectively as![]() , the integral of the power spectrum
, the integral of the power spectrum ![]() over the neighborhood
over the neighborhood ![]() at small values of
at small values of ![]() in (4.3) can be approximated by
in (4.3) can be approximated by
![]()
This form exactly coincides with the expression given in (4.2) obtained through the characteristic function formulation.
The approximations given in (4.6) and (4.8) cannot be proven easily as they involve limits of integration which directly depend on![]() . Furthermore, the mean value theorem point
. Furthermore, the mean value theorem point ![]() in (4.5) is arbitrary and cannot be determined beforehand for a given value of
in (4.5) is arbitrary and cannot be determined beforehand for a given value of![]() . The difficulties faced here emphasize the need for the method of stationary phase to formally prove Theorem 3.2.
. The difficulties faced here emphasize the need for the method of stationary phase to formally prove Theorem 3.2.
As we remarked before, the characteristic function and our wave function methods should not be treated as mere reformulations of each other. This distinction is further emphasized when we find our method to be computationally more efficient than the characteristic function approach in the finite sample-set scenario where we estimate the gradient density from N samples of the function S. Given these N sample values ![]() and their gradients
and their gradients![]() , the characteristic function defined in (4.1) needs to be computed for N integral values of
, the characteristic function defined in (4.1) needs to be computed for N integral values of![]() . Each value of
. Each value of ![]() requires summation over the N sampled values of
requires summation over the N sampled values of![]() . Hence the total time required to determine the characteristic function is
. Hence the total time required to determine the characteristic function is![]() . The joint density function of the gradient is obtained via the inverse Fourier transform of the characteristic function, which is an
. The joint density function of the gradient is obtained via the inverse Fourier transform of the characteristic function, which is an ![]() operation. The overall time complexity is therefore
operation. The overall time complexity is therefore![]() . In our wave function method the Fourier transform of
. In our wave function method the Fourier transform of ![]() at a given value of
at a given value of ![]() can be computed in
can be computed in ![]() and the subsequent squaring operation to obtain the power spectrum can be performed in
and the subsequent squaring operation to obtain the power spectrum can be performed in![]() . Hence the density function can be determined in
. Hence the density function can be determined in![]() , which is more efficient when compared to the
, which is more efficient when compared to the ![]() complexity of the characteristic function approach.
complexity of the characteristic function approach.
5. Experimental Evidence in 2D
We would like to emphasize that our wave function method for computing the gradient density is very fast and straightforward to implement as it requires computation of a single Fourier transform. We ran multiple simulations on many different types of functions to assess the efficacy of our wave function method. Below we show comparisons with the standard histogramming technique where the functions were sampled on a regular grid between
![]() at a grid spacing of
at a grid spacing of![]() . For the sake of convenience, we normalized the functions such that the maximum gradient magnitude value
. For the sake of convenience, we normalized the functions such that the maximum gradient magnitude value ![]() is 1. Using the sampled values
is 1. Using the sampled values![]() , we first computed the fast Fourier transform of
, we first computed the fast Fourier transform of ![]() at
at![]() , then computed the power spectrum followed by normalization to obtain the joint gradient density. We also computed the discrete derivative of S at the grid locations to obtain the gradient
, then computed the power spectrum followed by normalization to obtain the joint gradient density. We also computed the discrete derivative of S at the grid locations to obtain the gradient ![]() and then determined the gradient density by histogramming. For better visualization, we marginalized the density along the radial and the orientation directions. The plots shown in Figure 1 provide visual, empirical evidence corroborating our theorem. Notice the near-perfect match between the gradient densities computed via standard histogramming and our wave function method. The accuracy of the density marginalized along the orientations further strengthens our claim made in Section 1 about the wave function method serving as a reliable estimator for the histogram of oriented gradients (HOG). In Figure 2, we verify the convergence of our estimated density to the true density as
and then determined the gradient density by histogramming. For better visualization, we marginalized the density along the radial and the orientation directions. The plots shown in Figure 1 provide visual, empirical evidence corroborating our theorem. Notice the near-perfect match between the gradient densities computed via standard histogramming and our wave function method. The accuracy of the density marginalized along the orientations further strengthens our claim made in Section 1 about the wave function method serving as a reliable estimator for the histogram of oriented gradients (HOG). In Figure 2, we verify the convergence of our estimated density to the true density as ![]() in accordance with Theorem 3.2.
in accordance with Theorem 3.2.
6. Conclusions
Observe that the integrals
![]()
give the interval measures of the density functions ![]() and P respectively. Theorem 3.2 states that at small values of
and P respectively. Theorem 3.2 states that at small values of![]() , both the interval measures are approximately equal, with the difference between them being
, both the interval measures are approximately equal, with the difference between them being ![]() which converges to zero as
which converges to zero as![]() . Recall that by definition,
. Recall that by definition, ![]() is the normalized power
is the normalized power
![]()
Figure 1. Comparison results. 1) Left: Gradient magnitude density, 2) Right: Gradient orientation density. In each sub-figure, we plot the density function obtained from histogramming and the wave function method at the top and bottom respectively.
spectrum of the wave function![]() . Hence we conclude that
. Hence we conclude that
the power spectrum of ![]() can potentially serve as a joint density estimator for the gradient of S at small values of
can potentially serve as a joint density estimator for the gradient of S at small values of![]() , where the frequencies act as gradient histogram bins. We also built an informal bridge between our wave function method and the characteristic function approach for estimating probability densities, by directly trying to recast the former expression into the latter. The difficulties faced in relating the two approaches reinforce the stationary phase method as a powerful tool to formally prove Theorem 3.2. Our earlier result proved in [20], where we employ the stationary phase method to compute the gradient density of Euclidean distance functions in two dimensions, is now generalized in Theorem 3.2 which establishes a similar gradient density estimation result for arbitrary smooth functions in arbitrary finite dimensions.
, where the frequencies act as gradient histogram bins. We also built an informal bridge between our wave function method and the characteristic function approach for estimating probability densities, by directly trying to recast the former expression into the latter. The difficulties faced in relating the two approaches reinforce the stationary phase method as a powerful tool to formally prove Theorem 3.2. Our earlier result proved in [20], where we employ the stationary phase method to compute the gradient density of Euclidean distance functions in two dimensions, is now generalized in Theorem 3.2 which establishes a similar gradient density estimation result for arbitrary smooth functions in arbitrary finite dimensions.
As mentioned earlier, in [23] we have established error bounds in one dimension for the practical finite sample-set setting, wherein the gradient density is
![]()
Figure 2. Convergence of our wave function method as![]() . The value of
. The value of ![]() is steadily decreased from right to left, top to bottom.
is steadily decreased from right to left, top to bottom.
estimated from a finite, discrete set of samples, instead of assuming that the function is fully described over a compact set![]() . In the future, we plan to extend this work and derive similar finite sample error bounds for gradient density estimation in arbitrary higher dimensions.
. In the future, we plan to extend this work and derive similar finite sample error bounds for gradient density estimation in arbitrary higher dimensions.
Support
This research work benefited from the support of the AIRBUS Group Corporate Foundation Chair in Mathematics of Complex Systems established in ICTS-TIFR.
This research work benefited from the support of NSF IIS 1743050.
Appendix A. Proof of Lemmas
1) Proof of Finiteness Lemma
Proof. We prove the result by contradiction. Observe that ![]() is a subset of the compact set
is a subset of the compact set![]() . If
. If ![]() is not finite, then by Theorem (2.37) in [31],
is not finite, then by Theorem (2.37) in [31], ![]() has a limit point
has a limit point![]() . If
. If![]() , then
, then ![]() giving a contradiction. Otherwise, consider a sequence
giving a contradiction. Otherwise, consider a sequence![]() , with each
, with each![]() , converging to
, converging to![]() . Since
. Since ![]() for all n, from continuity it follows that
for all n, from continuity it follows that ![]() and hence
and hence![]() . Let
. Let ![]() and
and![]() . Then
. Then
![]()
where the linear operator ![]() is the Hessian of
is the Hessian of ![]() at
at ![]() (obtained from the set of derivatives of the vector field
(obtained from the set of derivatives of the vector field ![]() at the location
at the location![]() ). As
). As ![]() and
and ![]() is linear, we get
is linear, we get
![]()
Since ![]() is defined above to be a unit vector, it follows that
is defined above to be a unit vector, it follows that ![]() is rank deficient and
is rank deficient and![]() . Hence
. Hence ![]() and
and ![]() resulting in a contradiction.
resulting in a contradiction.
2) Proof of Neighborhood Lemma
Proof. Observe that the set ![]() defined in (2.2) is closed because if
defined in (2.2) is closed because if ![]() is a limit point of
is a limit point of![]() , from the continuity of the determinant function we have
, from the continuity of the determinant function we have ![]() and hence
and hence![]() . Being a bounded subset of
. Being a bounded subset of![]() ,
, ![]() is also compact. As
is also compact. As ![]() is also compact and
is also compact and ![]() is continuous,
is continuous, ![]() is compact and hence
is compact and hence ![]() is open. Then for
is open. Then for![]() , there exists an open neighborhood
, there exists an open neighborhood
![]() for some
for some ![]() around
around ![]() such that
such that![]() . By letting
. By letting![]() , we get the required closed neighborhood
, we get the required closed neighborhood ![]() containing
containing![]() .
.
Since![]() , points 1, 2 and 3 of this lemma follow directly from the inverse function theorem. As
, points 1, 2 and 3 of this lemma follow directly from the inverse function theorem. As ![]() is finite by Lemma 2.1, the closed neighborhood
is finite by Lemma 2.1, the closed neighborhood ![]() can be chosen independently of
can be chosen independently of ![]() so that points 1 and 3 are satisfied
so that points 1 and 3 are satisfied![]() . In order to prove point 4, note that the eigenvalues of
. In order to prove point 4, note that the eigenvalues of ![]() are all non-zero and vary continuously for
are all non-zero and vary continuously for![]() . As the eigenvalues never cross zero, they retain their sign and so the signature of the Hessian stays fixed.
. As the eigenvalues never cross zero, they retain their sign and so the signature of the Hessian stays fixed.
3) Proof of Density Lemma
Proof. Since the random variable X is assumed to have a uniform distribution on![]() , its density at every location
, its density at every location ![]() equals
equals![]() . Recall that the random variable Y is obtained via a random variable transformation from X, using the function
. Recall that the random variable Y is obtained via a random variable transformation from X, using the function![]() . The Jacobian of
. The Jacobian of ![]() at a location
at a location ![]() equals the Hessian
equals the Hessian ![]() of the function S at
of the function S at![]() . Barring the set
. Barring the set ![]() corresponding to the union of the image (under
corresponding to the union of the image (under![]() ) of the set of points
) of the set of points ![]() (where the Hessian vanishes) and the boundary
(where the Hessian vanishes) and the boundary![]() , the density of Y exists on
, the density of Y exists on ![]() and is given by (2.4). Please see well known sources such as [30] for a detailed explanation.
and is given by (2.4). Please see well known sources such as [30] for a detailed explanation.
For the sake of completeness we explicitly prove the well-known result stated in Integral Lemma 3.1.
4) Proof of Integral Lemma
Proof. Define a function ![]() by
by
![]()
Let![]() . Then,
. Then,
![]()
Letting ![]() and
and![]() , we get
, we get
![]()
As ![]() is
is ![]() integrable, by Parseval’s Theorem (see [21] ) we have
integrable, by Parseval’s Theorem (see [21] ) we have
![]()
By noting that
![]()
the result follows.
5) Proof of Cross Factor Nullifier Lemma
Proof. Let ![]() denote the phase of the exponential in the cross term (excluding the terms with constant signatures), i.e.,
denote the phase of the exponential in the cross term (excluding the terms with constant signatures), i.e.,
![]() (A.1)
(A.1)
Its gradient with respect to ![]() equals
equals
![]()
where ![]() is the Jacobian of
is the Jacobian of ![]() at
at ![]() whose
whose ![]() term equals
term equals ![]() (with a similar expression for
(with a similar expression for![]() ). Since
). Since![]() , we get
, we get![]() . This means that the phase function of the exponential in the statement of the lemma is non-stationary and hence does not contain any stationary points of the first kind. Let
. This means that the phase function of the exponential in the statement of the lemma is non-stationary and hence does not contain any stationary points of the first kind. Let
![]() (A.2)
(A.2)
Since![]() , consider the vector field
, consider the vector field ![]() and as before note that
and as before note that
![]() (A.3)
(A.3)
where ![]() is the divergence operator. Inserting (A.3) in the second line of (3.13), integrating over
is the divergence operator. Inserting (A.3) in the second line of (3.13), integrating over![]() , and applying the divergence theorem we get
, and applying the divergence theorem we get
![]() (A.4)
(A.4)
Here ![]() is the unit outward normal to the positively oriented boundary
is the unit outward normal to the positively oriented boundary ![]() parameterized by
parameterized by![]() . In the right side of (A.4), notice that all terms inside the integral are bounded. The factor
. In the right side of (A.4), notice that all terms inside the integral are bounded. The factor ![]() outside the integral ensures that
outside the integral ensures that
![]()
Appendix B. Well-Behaved Function on the Boundary
One of the foremost requirements for Theorem 3.2 to be valid is that the function ![]() have a finite number of stationary points of the second kind on the boundary for almost all
have a finite number of stationary points of the second kind on the boundary for almost all![]() . The stationary points of the second kind are the critical points on the boundary
. The stationary points of the second kind are the critical points on the boundary ![]() where a level curve
where a level curve ![]() touches
touches ![]() for some constant c [9] [10]. Contributions from the second kind are generally
for some constant c [9] [10]. Contributions from the second kind are generally![]() , but an infinite number of them could produce a combined effect of
, but an infinite number of them could produce a combined effect of![]() , tantamount to a stationary point of the first kind [9]. If so, we need to account for the contribution from the boundary which could in effect invalidate our theorem and therefore our entire approach. However, the condition for the infinite occurrence of stationary points of the second kind is so restrictive that for all practical purposes they can be ignored. If the given function S is well-behaved on the boundary in the sense explained below, these thorny issues can be sidestepped. Furthermore, as we will be integrating over
, tantamount to a stationary point of the first kind [9]. If so, we need to account for the contribution from the boundary which could in effect invalidate our theorem and therefore our entire approach. However, the condition for the infinite occurrence of stationary points of the second kind is so restrictive that for all practical purposes they can be ignored. If the given function S is well-behaved on the boundary in the sense explained below, these thorny issues can be sidestepped. Furthermore, as we will be integrating over ![]() to remove the cross-phase factors, it suffices that the aforementioned finiteness condition be satisfied for almost all
to remove the cross-phase factors, it suffices that the aforementioned finiteness condition be satisfied for almost all ![]() instead of for all
instead of for all![]() .
.
Let the location ![]() be parameterized by the variable
be parameterized by the variable![]() , i.e.,
, i.e.,![]() . Let
. Let ![]() denote the Jacobian matrix of
denote the Jacobian matrix of ![]() whose
whose ![]() entry is given by
entry is given by
![]()
Stationary points of the second kind occur at locations ![]() where
where![]() , which translates to
, which translates to
![]() (B.1)
(B.1)
This leads us to define the notion of a well-behaved function on the boundary.
Definition: A function S is said to be well-behaved on the boundary provided (B.1) is satisfied only at a finite number of boundary locations for almost all![]() .
.
The definition immediately raises the following questions: 1) Why is the assumption of a well behaved S weak? and 2) Can the well-behaved condition imposed on S be easily satisfied in all practical scenarios? Recall that the finiteness of premise (B.1) entirely depends on the behavior of the function S on the boundary![]() . Scenarios can be manually handcrafted where the finiteness assumption is violated and (B.1) is forced to be satisfied at all locations. Hence it is meaningful to ask: What stringent conditions are required to incur an infinite number of stationary points on the boundary? We would like to convince the reader that in all practical scenarios, S will contain only a finite number of stationary points on the boundary and hence it is befitting to assume that the function S is well-behaved on the boundary. The reader should bear in mind that our explanation here is not a formal proof but an intuitive reasoning of why the well-behaved condition imposed on S is reasonable.
. Scenarios can be manually handcrafted where the finiteness assumption is violated and (B.1) is forced to be satisfied at all locations. Hence it is meaningful to ask: What stringent conditions are required to incur an infinite number of stationary points on the boundary? We would like to convince the reader that in all practical scenarios, S will contain only a finite number of stationary points on the boundary and hence it is befitting to assume that the function S is well-behaved on the boundary. The reader should bear in mind that our explanation here is not a formal proof but an intuitive reasoning of why the well-behaved condition imposed on S is reasonable.
To streamline our discussion, we consider the special case where the boundary ![]() is composed of a sequence of hyper-planes as any smooth boundary can be approximated to a given degree of accuracy by a finite number of hyper-planes. On any given hyperplane,
is composed of a sequence of hyper-planes as any smooth boundary can be approximated to a given degree of accuracy by a finite number of hyper-planes. On any given hyperplane, ![]() remains fixed. Recall that from the outset, we omit the set
remains fixed. Recall that from the outset, we omit the set ![]() (i.e.,
(i.e.,![]() ) which includes the image under
) which includes the image under ![]() of the boundary
of the boundary![]() . Hence
. Hence ![]() for any point
for any point ![]() for
for![]() . Since the rank of Q is
. Since the rank of Q is ![]() and
and ![]() is required to be orthogonal to all the
is required to be orthogonal to all the ![]() rows of Q for condition 33 to hold,
rows of Q for condition 33 to hold, ![]() is confined to a 1-D subspace. So if we enforce
is confined to a 1-D subspace. So if we enforce ![]() to vary smoothly on the hyperplane and not be constant, we can circumvent the occurrence of an infinite number of stationary points of the second kind for all
to vary smoothly on the hyperplane and not be constant, we can circumvent the occurrence of an infinite number of stationary points of the second kind for all![]() . Additionally, we can safely disregard the characteristics of the function S at the intersection of these hyperplanes as they form a set of measure zero. To press this point home, we now formulate the worst possible scenario where
. Additionally, we can safely disregard the characteristics of the function S at the intersection of these hyperplanes as they form a set of measure zero. To press this point home, we now formulate the worst possible scenario where ![]() is a constant vector
is a constant vector![]() . Let
. Let ![]() denote a portion of
denote a portion of ![]() where
where![]() . Let
. Let ![]() and
and ![]() result in infinite number of stationary points of the second kind on
result in infinite number of stationary points of the second kind on![]() . As
. As ![]() is limited to a 1-D subspace, we must have
is limited to a 1-D subspace, we must have ![]() for some
for some![]() , i.e.,
, i.e.,![]() . So in any given region of
. So in any given region of![]() , there is at most a 1-D subspace (measure zero) of
, there is at most a 1-D subspace (measure zero) of ![]() which results in an infinite number of stationary points of the second kind in that region. Our well-behaved condition is then equivalent to assuming that the number of planar regions on the boundary where
which results in an infinite number of stationary points of the second kind in that region. Our well-behaved condition is then equivalent to assuming that the number of planar regions on the boundary where ![]() is constant is finite.
is constant is finite.
The boundary condition is best exemplified with a 2D example. Consider a line segment on the boundary![]() . Without loss of generality, assume the parameterization
. Without loss of generality, assume the parameterization![]() . Then
. Then![]() . Equation (B.1) can be interpreted as
. Equation (B.1) can be interpreted as ![]() where,
where,![]() . So if we plot the sum
. So if we plot the sum ![]() for points along the line, the requirement reduces to the function
for points along the line, the requirement reduces to the function ![]() not oscillating an infinite number of times around an infinite number of ordinate locations
not oscillating an infinite number of times around an infinite number of ordinate locations![]() . It is easy to see that the imposed condition is indeed weak and is satisfied by almost all smooth functions. Consequently, we can affirmatively conclude that the enforced well-behaved constraint (B) does not impede the usefulness and application of our wave function method for estimating the joint gradient densities of smooth functions.
. It is easy to see that the imposed condition is indeed weak and is satisfied by almost all smooth functions. Consequently, we can affirmatively conclude that the enforced well-behaved constraint (B) does not impede the usefulness and application of our wave function method for estimating the joint gradient densities of smooth functions.