Trading Frequency Anomalies in Infant Markets: The Test for Returns and Sensitivity of Shares and Portfolios ()
1. Introduction
The inception of Capital Market Theory and Capital Asset Pricing Model (CAPM) introduced by Treynor (1962); Sharpe (1964); Lintner (1965) and Mossin (1966) has opened the debate about the relationship between the share returns and market index measured returns. While CAPM hypothesis claimed a direct positive linear relationship between returns of shares and market returns, studies testing the hypothesis in frontier and infant stock markets1 show different results. Mazviona (2013) reported negative linear relationship between returns of shares and returns of index of the stocks traded in Zimbabwe stock exchange between 2009 and 2012. Matteev (2004) found that the relationship between share returns and market returns was flat in Bulgaria stock exchange for the stocks traded between 1998 and 2002. Iqbal & Brooks (2007) pointed out that the relationship between share returns and market returns is non-linear for the stocks traded in Karachi stock exchange between 1992 and 2006, although the market performance was backed with high level of liquidity and trading activities. The complex behavior of beta in frontier and infant markets resulted in confusion on interpreting the CAPM, and this has further lead to the conclusion that the CAPM is inapplicable in these infant markets.
In a recent study of African stock markets by Essingone & Diallo (2019) in West Africa Economic and monetary Union Regional Exchange of Securities, Asymmetric Response Model (ARM) was considered as an alternative model for CAPM in estimating risk. However, asymmetric nature of risk was still existed due to the lack of attractiveness of shares listed in, lack of speculative behaviour among investors, tendency of holding stock for long and fearing of getting loss. It was stressed by Asad, Khan, & Faiz (2018) that in developing countries, investors were more sensitive to price volatility. Most of potential investors preferred to invest in riskless financial assets due to expected profit in the share invested. However, the scholars overlooked to demonstrate quantitatively the relationship between the behavior of holding stock with expected gain or loss as well as the risk of getting that loss. Experience gained from developed markets showed that the investors who traded frequently generated higher returns than infrequently traded investors (Busse, Tong-Lin, Tong-Qing, & Zhang-Zhe, 2019). But the results may prove different in frontier and infant markets due to the low liquidity of the shares traded.
Overall, quantitative validation of influence of trading frequency on infant stock markets received limited attention by scholars and practitioners in recent decades. This may be due to the wide gap existed between advanced and infant markets. This study aims to narrow the gap between advanced and infant markets by adding another piece of puzzle on share return and beta behavior. The central theme of this study is to examine the trading frequency anomalies in infant markets. Specifically, this study explains the effect of share trading frequency on share returns and beta and to what extent the effect will emerge when portfolios of the same shares are constructed. The infant stock markets in Africa face the challenges of lack of knowledge of share trading, trading platform software’s and their maintenance, government encouragement etc. On the brighter side, they try to follow their neighbors and strong markets to learn. This sincere attempt will help them to overcome the challenges and lead them to grow. This article has provided indications to the policy makers and regulators of East Africa stock markets and to spread investment knowledge. The reminder of this article is presented in five sections. Section two discusses related literature. Section three covers the data and methodology adopted. Section four presents the results and discussion, while section five concludes the paper.
2. Related Literature
Trading frequency is defined as the number of days in which a share shows price change to the total number of trading days within the market (Bernales, Beuermann, & Cortazar, 2014; Armitage & Brzeszczynski, 2011; Oprea, 2015). According to Reuters (2015), the threshold trading frequency for developed markets is 90%, emerging markets 80% and frontier markets 50%. Recent studies conducted in emerging and frontier markets related to the infrequently trading with share liquidity problem and trading information (Janabi, 2007; Vidovic, Poklepovic, & Aljinovic, 2014). The shares which are infrequently traded may be associated with long term holding stock by investors or brokers who are risk-averse, and this directly results in illiquidity of shares and vis-versa. Likewise, the frequently traded shares have low probability of informed trading than infrequently traded that result to be less risky. In terms of firm size, small firms are less-frequently traded than large firms, and market with many small firms have higher level of infrequently trading shares and vise-versa (Oprea, 2015). In other literature, existence of infrequently trading shares is a barrier for stock market development and also to foreign investors (Minovic, 2012). This is associated with inefficient market infrastructure, high transaction costs, high bid-ask spreads and a small number of traders that lead to order imbalance and poor performance of the stock markets.
The relationship between share returns and trading frequency has been explained in multidimensional forms among scholars. Busse, Tong-Lin, Tong-Qing, & Zhang-Zhe (2019) found that shares which were frequently traded generated higher returns compared to shares which were infrequently traded. Similarly, Karaa, Slim, & Hmaied (2018) concluded that infrequently traded shares are associated with low returns. They stressed that infrequently trading or non-trading were the signals of bad news, which slows down the price of stock. The investors traded more frequently when there was good news. However, the existence of zero returns was very common in infrequently traded shares and markets at large. This happened due to high probability of informed trading and investors always trade-off between cost and benefit. The study of Minovic (2012) highlighted that investors chose not to trade when cost of trading is higher than the benefit that would result in zero or negative returns. Zero returns measure can be used to explain the liquidity of shares and market at large. It can be measured by taking the number of zero return days in a year to the total number of trading days in a year.
Abnormal behavior of beta was associated with non-trading or infrequently trading a long time ago since the study of Scholes & Williams (1977) as well as Dimson (1979). They both found that infrequently traded shares were associated with low beta while those shares which were frequently traded produced high beta. They highlighted that the stability of beta in infrequently trading shares was influenced by “intervalling” effect, and the effect would be more significant when return interval was short. Similar finding was observed by study of Matteev (2004), and Armitage & Brzeszczynski (2011)
The study of Mensah (2013) and Mensah (2015) both highlighted that portfolio beta decreased with the increase in portfolio size. Similarly, portfolio returns increased with the increase of portfolio size to the maximum of seven shares out of ten shares used. Interestingly, average portfolio returns were higher in value weighted portfolio than the equal weighted portfolio, and this was due to difference of trading frequency among shares used in portfolio construction. However, both Mensah (2013) and Mensah (2015) overlooked to test differences between weighted portfolio based on increasing frequency or decreasing frequency. The study of Busse et al. (2019) found that when funds were allocated equally, the portfolio produced higher return than the weighted portfolio. Also, the portfolio of frequently traded shares outperformed the portfolio of infrequently traded shares.
The question of fund allocation is still debated among scholars and practitioners. Sirucek & Kren (2015) allocated the funds based on mean returns of a share. What’s more, they used random fund allocation among shares whereby the funds were allocated as per random number generated using computer. Further, they found that the random approach showed better results than performance-based approach, which was also supported by Ramasamy et al. (2015) who used MATLAB program to compute the random allocation of funds and found the portfolios produced a higher return with comparable lower risk. This was contrary to the study of Pollak (2011) that used naive method of fund allocation. In this method, the funds were allocated among shares subject to the principle that the total weight must not exceed one. Based on the previous studies, the funds in this study were allocated randomly and on weighted average basis in order of increasing and decreasing the frequency of shares traded in DSE as shown in Figure 1.
This study presents a practical and simple investment technique that investors
![]()
Figure 1. Flow of funds in CAPM portfolio construction and performance assessment.
can use prior to making any investment decision by introducing Share Trading Frequency Ranking (STFR). Also, it incorporates several methods of fund allocation to investigate the significance of trading frequency when those shares are mixed. A recent study by Busse et al. (2019) focuses on trading frequency on investors and found that those investors who trade frequently generate abnormal returns than those who are traded less frequently His study overlooked to address the situation when many investors are traded on the same companies. Karaa et al. (2018) emphasized that volatility also increases when trade intensity increases but this finding is only restricted to high frequently traded shares—referred as blue chip stocks. Oprea (2015) mixed both frequently and infrequently traded share and found that the frequently traded shares generate higher beta than infrequently traded shares. Although Oprea (2015) was interested in the intervalling effect of beta estimated using market model, the effect of trading frequency on returns was not reported.
3. Data and Methodology
The daily closing share prices of 22 companies from different sectors (Industrial and Allied, Commercial Service, Banks, Finance & Investment) for 246 days were collected from the Dar Es Salaam Stock Exchange (DSE) for the year 2018. The selected companies are those listed before 1st January 2018 and throughout 2018. Similarly, DSE Index (DSEI) of the same period was also extracted. Since both closing prices and DSEI are non-stationery, prices were converted into returns to make data stationery for further analysis. Baumöhl & Lyócsa (2009) insisted that continuing to analyze non-stationary data will produce spurious results. Young & Shahabi (2005) explained that the trend in non-stationery data can be removed by taking the natural logarithm of differences of price of the current and the previous day to avoid non-stationarity of data. This resulted in share returns corresponding to 245 days.
Thereafter, shares with zero returns throughout the year with zero trading frequency were dropped from the study and only 17 shares were qualified for further analysis. The MATLAB source code that incorporates CAPM was developed and is shown in stepwise below. The results were annualized to understand the yearly movement of mean returns and beta as suggested by Diebold et al. (1997). Thus 15 portfolios were constructed using 17 shares with the first portfolio (P1) starting with three shares (3S). In the subsequent portfolios, the number of shares increased one by one to get 15 portfolios with 17 shares. The portfolio returns and portfolio beta were computed, leading to the Treynor ratio, which ultimately decided the performance of the portfolio.
3.1. Conversion of Share Price to Share Returns
By using the command “r1 = price2ret (x (1: n, :))”, the share prices were converted to geometric returns using Equation (1).
(1)
where,
is the share price of second day,
is the share price of previous day and, r is the daily share returns. The returns
for shares
in time
will be presented in matrix form as shown in Equation (2).
(2)
3.2. Risk Free Rate
The risk free rate (rf) was the base lending rate (br) where in this study was 3.8% annually that converted them to daily, since the share returns are in daily basis. The command “rf = br/365” was used.
3.3. Computation of Market Mean Returns
The market returns were calculated from market index using the Equation (3). The command “rm = mean (r (: end))” was used to compute the market mean returns.
(3)
where,
is the market returns,
is the market mean returns and n is the number of shares.
3.4. Computation of Share Beta
The share’s beta is computed as a regression coefficient between market returns and shares returns. The Equation (4) can be used to compute the share’s beta. The command “beta = regress (r1, [ones (n, 1) r (1: n, end)])” was used to compute it.
(4)
where,
is the share beta,
is the covariance of share i and market index and
is the variance of market index. The share’s beta
computed in Equation (4) was annualized using the Equation (5).
(5)
where,
is the annualized beta and, n is the number of trading days. The vector of annualized share’s beta
from
, will be formed as shown in Equation (6).
(6)
3.5. Computation of Share Mean Returns
The mean returns of shares were calculated using Equation (7) that was composed using command “RR = (rf + beta (2) * (rm − rf))”.
(7)
where,
is the share beta,
the mean returns of shares and,
is the risk free returns. The daily portfolio share returns
computed in Equation (7) were annualized using the Equation (8).
(8)
where,
is the annualized mean returns and, t is the total number of days in a year. The annualized share mean returns vector for
, was formed as presented in Equation (9).
(9)
3.6. Share Treynor Ratio
The annualized Treynor ratio was calculated by dividing the difference of annualized share returns and annual risk free returns with annualized share beta as shown in Equation (10) that was composed using command “itr = (xrr-rf)./bt”.
(10)
3.7. Trading Frequency
Trading frequency,
is defined as the number of days in which share shows price changes,
to the total number of trading days within the market,
. The Equation (11) was used to compute them.
(11)
3.8. Zero Return Measure
This can be measured by taking ratio of number of zero return days,
of share i to the total number of trading days T as shown in the Equation (12).
(12)
3.9. Proportion of Fund Invested
1) The random weights were generated using command “bi = randn (1, i); w = bi./sum (bi)”.
2) The weight in order of decreasing trading frequency was generated using command “bi = linspace (j, 1, j); w = bi./sum (bi)”.
3) The weight in order of increasing trading frequency was generated using command “bi = linspace (1, j, j); w = bi./sum (bi).
Thereafter, weight vectors for each one were generated as shown in Equation (13).
(13)
3.10. Annualized Portfolio Beta
The annualized portfolio beta
was calculated by multiplying the annualized share’s beta vector (Equation (6)) with weight transpose vector (Equation (13)) as shown in the Equation (14). The command “pb1 = bt (1: j) *w” was used for the computation.
(14)
3.11. Annualized Portfolio Mean Returns
The annualized portfolio mean return
was calculated by multiplying the annualized share mean return vector (Equation (9)) with weight transpose vector (Equation (13)) as shown in Equation (15). The command “pr1 = xrr (1: j) *w'” was used for the computation.
(15)
3.12. Annualized Portfolio Treynor Ratio
The annualized portfolio Treynor ratio was computed by dividing the difference between annualized portfolio mean returns computed in Equation (15) and risk free returns with annualized portfolio beta computed in Equation (14) as shown in Equation (16) using command “(ter1 = pr1 − rf)./pb1” was used.
(16)
4. Results and Discussion
The results in Table 1 show the overall trading frequency of share listed in DSE as well as the frequency of frequently and infrequently traded shares. The overall trading frequency in DSE is 42.26%. According to Thomas Reuters’s (2015) classification, the lowest class is frontier markets with a minimum threshold of
1) The shares in the first column are presented in short form and those requiring detailed analysis are explained in full in the text body. 2)
represents the number of days in which the share shows price changes
is the total number of trading days within the market and
is the trading frequency.
50% trading frequency. However, there are five shares traded frequently with average frequency of 82.12%, including Acacia Mining (ACA) (92.65%), East African Breweries Limited (EABL) (84.08%), Jubilee Holding Limited (JHL) (83.67%), National Media Group (NMG) (81.63%) and Kenya Commercial Bank (KCB) (68.57%). However, there is a big gap between frequently and infrequently traded shares. The most infrequently traded share was Mwalimu Commercial bank (MCB) with trading frequency of 2.45%. The frequently traded shares are cross-listed in other stock exchanges and the list of infrequently traded shares is domestic shares of DSE. This highlights that investors in DSE trade more on foreign shares than on domestic shares. This finding is in line with the study of Vinh-Vo (2019) and Nguyeni (2017) who found that foreign investors perform better even in emerging markets because they are well equipped with soft skills and resources. The investors can access to information easily in cross-listed shares compared to domestic shares. Therefore, there is a need for DSE to list domestic shares in other East African stock exchanges in order to improve the trading skills of domestic investors. This will eventually lead to an increase of efficiency in trading.
The results presented in Table 2 portrait the annualized average return, beta and performance measured by Treynor ratio of each share in order of trading frequency. The frequently traded shares generate average returns of maximum of 2.31%, whereas infrequently traded shares record an average return of 4.13%. Similarly, minimum returns of frequently traded shares were −9.43%, while that of infrequently traded shares are −0.42%. Overall, infrequently traded shares in DSE generate higher returns than frequently traded shares. This finding contradicts with that of Busse et al. (2019) and Karaa et al. (2018) who posited that frequently traded shares generate higher returns than less frequently traded shares.
In DSE, frequently traded shares are more volatile in terms of beta than infrequently traded shares. This means that the highly frequently traded shares have high degree of price fluctuations than the DSE index. Likewise, the low frequently traded shares have lower degree of fluctuation than the DSE index.
![]()
Table 2. Annualized share returns, beta, Treynor ratio and zero returns of frequently traded shares.
 ,
,  ,
, 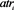 and
and 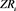 represent annualized share mean returns, beta, Treynor ratio and zero returns respectively.
represent annualized share mean returns, beta, Treynor ratio and zero returns respectively.
These findings are quite opposite to that of Mensah (2013) although they were in line with early works of Scholes & Williams (1977) as well as Dimson (1979). Abnormal observation found National Media Group (NMG) classified among frequently traded shares and Tanzania Cement Company (TCC) among infrequently traded shares. Results showed that their annualized beta,  and 38.2 respectively. This is due to the absence of strong positive correlation between NMG and TCC with DSE market returns. Overall, infrequently traded shares perform better than frequently traded shares. Similarly, results also showed that all shares which are frequently traded produce negative Treynor ratio with a maximum of −0.47 while the shares which are infrequently traded produce positive Treynor ratio up to 1.71.
and 38.2 respectively. This is due to the absence of strong positive correlation between NMG and TCC with DSE market returns. Overall, infrequently traded shares perform better than frequently traded shares. Similarly, results also showed that all shares which are frequently traded produce negative Treynor ratio with a maximum of −0.47 while the shares which are infrequently traded produce positive Treynor ratio up to 1.71.
The effect of trading frequency further analyzed on 15 self-constructed portfolios among the shares traded in DSE is shown in Table 3. The portfolio constructed in the order of increasing frequency, decreasing frequency and random mix. They differ in terms of return, risk and performance. The portfolio constructed by random mix recorded a maximum average return of 5.88% with 10 shares in the portfolio and minimum of 2.09% with 6 shares in the portfolio. However, the returns of portfolios constructed in order of decreasing of trading
![]()
Table 3. Annualized share returns, beta, Treynor ratio and zero returns of frequently traded shares.
1) “P” stands for Portfolio, which starts from Portfolio 1 (P1) to Portfolio 14 (P15); 2) “S” stands for Shares, which start from 3-Shares (3S) to 17-Shares (17S); 3) ,
, 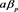 and
and 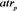 represent annualized portfolio mean returns, portfolio beta and portfolio Treynor ratio respectively.
represent annualized portfolio mean returns, portfolio beta and portfolio Treynor ratio respectively.
frequency produce maximum average return of 2.04 with 3 shares in the portfolio and minimum average return of 0.29% with 6 shares in the portfolio. Contrary to portfolio constructed in order of increasing trading frequency, maximum average returns of 3.11% with 5 shares in the portfolio and minimum of 2.06% with 17 shares in the portfolio are shown. The portfolio beta increases from 3.11 for 3 shares portfolio to 5.78 for 6 shares portfolio. Thereafter, when more shares are added randomly, results show negative beta continuously up to 17 shares. Beta produced in the portfolio formed in order of decreasing trading frequency of shares behaves differently. It increased suddenly from 7.20 for 3 shares to 30.72 for 6 shares. Thereafter, when more infrequently traded shares were added, the portfolio beta decreased until it reached 19.40 with 17 shares portfolio. Contrary to beta produced in the portfolio formed by order of increasing frequency of share. It was increased continuously from −6.10 for 3 shares to 7.06 for 17 shares.
Most of the portfolio constructed in all three approaches was not performed well as they produced negative Treynor ratio. For random allocation portfolio, the negative Treynor ratio is mainly associated with negative beta produced. For the portfolio constructed in the order of increasing trading and decreasing trading frequencies, negative Treynor ratio was observed. The results contradict with the study of Busse et al. (2019) who found portfolio of frequently traded shares perform better than infrequently traded shares. The methodology of computing portfolio performance differed as they used technical approach to determine the performance of shares before mixing them equally and allocating based on performance, which, however, was measured by means of Treynor ratio in this study. Besides, they conducted their study in advanced market while this study was conducted in infant market.
Analysis of Variances
Table 4 shows ANOVA test results for portfolio mean returns, beta and Treynor ratio of the portfolios constructed in various fund allocation. The random allocation has higher average returns (µ = 3.78) and higher variance (σ = 2.01) between one portfolio and another. However, the portfolio weighted in increased frequency records higher average return (µ = 2.49) than the portfolio weighted in decreasing frequency that has µ = 0.84 although it shows smaller variance (σ = 0.12). Generally, there is a significant difference of portfolio mean returns with (p ≤ 0.00) when portfolio contracted by random allocation of shares or weighted
![]()
Table 4. Portfolio behavior on various allocations of fund.
in order of trading frequency. Generally, the portfolio constructed by random allocation of both shares traded frequently and infrequently generates highest returns. While, the returns of the portfolio constructed in order of trading frequency were found to increase when infrequently traded shares were added in the portfolio and to decrease when frequently traded shares were added in the portfolio.
To observe the reaction of beta, the portfolio formed by random allocation produce negative beta with average of (µ = −15.30) with huge variance across portfolio which is quite opposite with beta produced in a weighted portfolio in order of frequency. The portfolio weighted in increasing frequency record minimum beta of average (µ = 1.71) while portfolio weighted in decreasing frequency show maximum beta with average (µ = 23.48). Overall, the difference among beta produced in those three approaches is significant with (p ≤ 0.00). This is contrary to Treynor ratio where all of them have average negative performance. Although, portfolio constructed in order of decreasing frequency is much better compare to others yet the difference is not significant as (p = 0.34). Figure 2 illustrates the difference of portfolio mean returns, beta and Treynor ratio for the portfolio constructed based on increasing trading frequency (Inc. TF), decreasing trading frequency (Dec. TF) and random allocation (Random).
5. Conclusion
Portfolio construction is important in infant markets such as DSE. Out of 17 shares selected, 15 portfolios were designed based on frequency of trading. Only five shares in DSE are traded frequently with an average trading frequency of 82.12%. All the frequently traded shares were cross-listed from other stock exchanges. The remaining 12 shares were infrequently traded with an average of 25.65% throughout the year and most of them are domestic listed shares. Overall, DSE can be ranked below frontier market class according to Thomas Reuters (2015) market classification since the average market trading frequency is 42.26%. The infrequently traded shares in DSE generate higher returns than frequently traded shares. Most frequently traded shares are the least performing
![]()
Figure 2. The difference of mean returns, beta and Treynor ratio in various allocation of funds.
and produce minimum returns compare to the shares which are infrequently or rarely traded. It is wise to say that investors in DSE trade more in foreign shares than domestic shares although domestic shares generate higher returns. Generally, the portfolio constructed by random allocation of both share traded frequently and infrequently generates the highest returns. However, the returns of the portfolio constructed in order of trading frequency are found to increase when infrequently traded shares were added in the portfolio and decreased when frequently traded shares were added in the portfolio. The portfolio beta decreases to two-digit negative when random mixed portfolios are formed, and it also increases two-digit positive when portfolios are formed in order of decreasing frequency and change from negative to single-digit positive when portfolios are designed in order of increasing frequency. Overall, portfolios formed in all three approaches did not perform well as most of them generates negative Treynor ratio. This may be due to minimum returns that portfolio produced compare to risk free returns in DSE. We suggest that the DSE domestic shares are to be listed in other East African Stock exchanges in order to improve trading skills and portfolio performance. This will in turn increase trading frequency. Essentially, it will help DSE grow and directly lead to the growth of Tanzania Economy. Since this study was conducted only in DSE using one-year data, other studies can be extended to other markets with similar characteristics and comparative studies can be done. Also, data range can be extended to more than one year in order to observe pattern of trading frequency influence. Overall, the market model was adopted to estimate the returns and sensitivity of shares and portfolios, and future studies can be conducted using lag distribution model as suggested by Dimson (1979) to investigate the differences of the results generated between models.
NOTES
1Infant Stock markets refer to those markets with trading frequency below 50 percent, and this is adopted from Thomas Reuters (2015)’s lowest classification of frontier market. This term “Infant market” was also used by Lukanima (2014) in his study about price discovery and memory effect.