Design of Self-Assembling Molecules and Boundary Value Problem for Flows on a Space of n-Simplices ()
1. Introduction
Self-assembling molecules are ubiquitous in nature, among which are proteins, nucleic acids (DNA and RNA), peptides and lipids. Recognizing the ability of biomolecules to self-assemble into various 3D shapes at the nanoscale, researchers are mimicking the bottom-up self-assembly strategy for precise engineering of complex nanostructures [1] [2] [3]. As suggested by Gellman in [3], “realization of the potential of folding polymers may be limited more by the human imagination than by physical barriers”.
However, we have not yet identified the underlying general principles that govern the engineering of self-assembling molecules. The question is
“How to obtain a well-defined shape with desired properties by folding a chain of subunits,”
where properties are determined by the precise spatial arrangement of the subunits on the surface. In the case of proteins, on the surface are “active sites” formed by a set of amino acids arranged in a specific configuration, through which proteins carry out their function. Note that a pair of subunits adjacent on the surface are often far apart along the chain.
The question shown above is divided into two sub-questions. One is to find a backbone conformation called target structure that forms a shape of the desired properties. The other is to find a chain of subunits that adopts the target structure. In this paper, we shall discuss the former of these two sub-questions from the viewpoint of the discrete differential geometry of n-simplices.
Using the mathematical toy model proposed in [4] [5], we shall represent self-assembling molecules as a union of trajectories of 3-simplices (i.e., tetrahedrons). Then, the former sub-question is rephrased as a “boundary value problem” for flows on a space of 3-simplices:
“Given a triangular flow (i.e., desired properties). Find a tetrahedral flow (i.e., well-defined shape) that induces the triangular flow as its surface flow.”
In this paper, we first give an introduction to the discrete differential geometry of n-simplices. In addition to the case of triangles and tetrahedrons, we also consider the case of 1-simplices (line segments) in order to handle surface flows induced on a union of trajectories of triangles. After giving a definition of boundary value problem for flows on a space of n-simplices, we shall consider the boundary value problem with some examples. For simplicity, we mainly deal with flows of triangles and their surface flows of line segments. Finally given is a characterization of two types of surface flows of line segments, i.e.,
-embeddable surface flow and locally
-embeddable surface flow. This distinction may be essential in characterizing some important properties of biomolecules such as “allosteric regulation” (i.e., long distance interactions between subunits) as mensioned in [5]. Some open problems are also given along the way.
We believe this paper will open up a new perspective for the engineering of self-assembling molecules and bring about further advances in collaboration between mathematics and other disciplines in life science.
Finally, Genocript (http://www.genocript.com) is the one-man bio-venture started by the author in 2000 which is developing software tools for protein structure analysis. In particular, the author is not affiliated with any research institution.
2. Previous Works
Actively researched self-assembling molecules include biomolecules such as DNA (i.e., polynucleotides), proteins (i.e., polypeptides), and unnatural molecules such as foldamers (i.e., unnatural oligomers). As for approaches from mathematics, there are no known attempts other than sporadic applications of graph theory in the engineering of DNA- and protein-based nanostructures.
2.1. DNA-Based Nanostructures
Self-assembling DNA-based nanostructures have been extensively studied, as the specificity of Watson-Crick base pairing provides ease of control over interactions between DNA strands. Well known in the field of DNA nanotechnology is the scaffolded DNA origami method [1], in which a long single-stranded DNA (called scaffold strand) is folded into arbitrary shapes with the help of many short single-stranded DNAs (called staple strands) in a single step.
For two-dimensional shapes, a target shape is approximated by folding a scaffold strand back and forth in a raster fill pattern. The target shape is then obtained as a flat sheet of antiparallel DNA double helices which is cross-linked by lots of staple strands.
Three-dimensional shapes are obtained by stacking flat sheets of antiparallel DNA double helices to form a closely packed pleated layer structure [6]. To construct space-filling multilayer objects, flat sheets are packed onto a honeycomb lattice, a square lattice, or a hexagonal lattice [7].
2.2. Protein-Based Nanostructures
Protein-based nanostructures have several advantages over DNA-based nanostructures, such as structural richness, functional versatility, and cost effective manufacturing. DNA-based nanostructures consist of four nucleic acids, and are prepared by chemical synthesis. In contrast, protein-based nanostructures consist of 20 amino acids, and are manufactured by biotechnological methods. One of the disadvantages is the much more complicated design rules, due to the contribution of many cooperative and long range interactions between amino acids.
There are two types of approaches in finding a polypeptide that folds into a specified 3D shape (i.e., protein design). One is the design of proteins with a desired backbone structure. The other is the design of proteins with desired functions (i.e., desired active sites or desired interacting surfaces).
In general, structural design starts with a target backbone structure description. Target descriptions are usually given as a 2D schematic diagram [8] [9]. In the diagram, 3D backbone structures are represented as a sequence of local structural patterns (such as alpha-helices and beta-strands) with sets of pairwise spatial relationships between them.
A set of target backbone structures consistent with the diagram are often generated by assembling short backbone fragments from existing proteins [10] [11] [12]. Note that it is not clear whether the target structure is designable, i.e., there exists an amino acid sequence that would adopt the conformation in nature. By reusing naturally occurring protein fragments, it is ensured that new backbone structures are more likely to be designable.
On the other hand, functional design generally starts with a target active site or a target interacting surface description. A target active site description includes a target reaction and a model of the reaction mechanism [13]. Active sites usually consist of functional residues located in different regions (i.e., disjoint fragments) of the linear polypeptide chain. A three-dimensional arrangement of the functional residues is derived from the given description. A set of existing proteins is then searched for backbones that can support the arrangement of the functional residues [14] [15], onto which the target active site is grafted. For now, it is difficult to generate new backbones from a set of disjoint fragments so that the resulting backbone accommodates the spatial arrangement of the given set of disjoint fragments [12].
2.3. Protein Origami
In addition, there is another approach to constructing self-assembled protein nanostructures, called “protein origami” [2] [16]. This approcach is based on the specificity of pairwise interactions between coiled-coil-forming polypeptide segments rather than the numerous cooperative interactions between amino acids. The coiled-coils are composed of two intertwined helical segments that wrap around each other to form a supercoiled structure, where each segment binds only to its designated partner and does not interact with the others (i.e., orthogonal).
The orthogonal coiled-coil-forming segments are concatenated in a specified order to form a single polypeptide chain, which folds into a polypeptide polyhedron as the orthogonal interacting segments assemble into coiled-coils with their designated partners. For example, a tetrahedron is self-assembled from a polypeptide chain consisting of 12 coiled-coil forming segments separated by flexible linkers. The generated 6 coiled-coils correspond to the 6 edges, and the linkers are located on the vertices. The sequential arrangement of the 12 coiled-coil forming segments and the orientation of each coiled-coil pair are obtained as a double Eulerian path in a tetrahedron, i.e. an oriented path that traverse each of the 6 edges of the tetrahedron exactly twice. The existence of double Eulerian paths is guaranteed by graph theory, because all the vertices of a double tetrahedral graph have an even degree.
2.4. Unnatural Molecules
To realize the full potential of self-assembling molecules, researchers are also working on the design of unnatural molecules with structures and functionalities not found in nature.
Most of the research so far has focused on reproducing local structural patterns of proteins such as helices and sheets [17] [18] [19]. It is still a major challenge to pack the local structural patterns obtained into a uniquely specified compact conformations [20].
So far no foldamaer is known that displays a given compact conformations [21]. Natural proteins typically require more than 100 residues to display stable compact conformation. However, careful choice of preorganized monomers may lead to foldamers of less than 40 residues with stable compact conformation [3].
2.5. Flows of n-Simplices
The author is unaware of similar studies by other researchers on flows of n-simplices.
As for differential geometry on a space of n-simplices, differential geometry on polyhedra (such as differential forms on n-simplices) has been studied from the view point of classification of geometrical objects (For example, see [22] ). In particular, n-simplices have been played an important role in homological algebra [23]. However, shapes of trajectories of n-simplices are not explicitly considered there.
As for surfaces consisting of triangles, they have been studied as discrete analogues of smooth geometric objects [24]. Typically, they are obtained as a result of the triangulation of the surfaces of real world objects in 3D computer graphics. However, there are no known studies on flows of triangles on the triangular surface.
3. Flows of n-Simplices
This paper proposes a novel mathematical approach for the design of self-assembling molecules, which is based on the discrete differential geometry of n-simplices [4] [5]. In our approach, self-assembling molecules are represented as a union of trajectories of tetrahedrons. The “spatial arrangement of the subunits (such as amino acids, nucleic acids, or others)” on the surface of a molecule then corresponds to the “flow of triangles” induced on the surface of a union of trajectories of tetrahedrons. In this section, we shall give an introduction to the discrete differential geometry of n-simplices.
In the following,
denotes the set of all natural numbers,
denotes the set of all integers,
denotes the set of all real numbers, and
(
) denotes the n-dimensional Euclidean space.
For space saving purposes, the coordinates of points in
are represented by a monomial in n indeterminates
. For example, point
is represented by
. Points
,
,
are represented by 1,
,
, respectively. Moreover,
denotes the point
, where
.
3.1. General Case
3.1.1. Flows on an n-Simplex Space
First of all, we shall define a space of n-simplices, upon which flows of n-simplices are defined. The topology of the space is defined using “adjacent” relationship between n-simplices.
Definition 1 (n-simplex). Let
. An n-simplex is the convex hull of
affinely independent points in
(i.e., points not lying in a
-dimensional subspace). The convex hull of
points
is denoted by
, i.e.,
Then,
(
) are called the vertices of
. Let s be an n-simplex. The set of all the vertices of s is denoted by
.
For example, a 0-simplex is a point, a 1-simplex is a line segment, a 2-simplex is a triangle, a 3-simplex is a tetrahedron.
Definition 2 (k-face). Let
and
. Let s be an n-simplex. A k-face of s is the convex hull of any
vertices of s. A 0-face is a vertex of s. A 1-face is called an edge of s. An
-face is called a facet of s. Note that the n-face is s itself.
For example, let
be a tetrahedron. Then, s has 6 edges
(
) and 4 facets
(
). Moreover,
.
Definition 3 (n-simplex space). Let M be a set of n-simplices. M is called an n-simplex space if each n-simplex is connected to other n-simplices in such a way that,
for
facet u of
, uniquely
such that
.
In particular, each n-simplex is connected to
“adjacent” n-simplices through its
facets.
Example 1. We would obtain an n-simplex space by partitioning
into pieces of n-simplices. Shown in Figure 1(a) is a triangle space
obtained by partitioning
into pieces of triangles.
Definition 4 (k-face neighborhood N(u)). Let M be an n-simplex space and
. Let u be a k-face of s. The k-face neighborhood
of u is a set of n-simplices of M which contain u:
For
, we obtain
. Note that every facet neighborhood consists of two n-simplices. We shall use the fact when defining local trajectories of n-simplices (See just above Definition 6).
Now let us define flows of n-simpleces on an n-simplex space.
Definition 5 (Tangent space T(s)). Let s be an n-simplex. The tangent space
at s is the set of all the edges of s, i.e.,
![]()
Figure 1. Flow of triangles. (a) A triangle space
obtained by partitioning
into pieces of triangles; (b) Gradients of triangles of
. For each triangle
, the gradient (i.e., the set of edges assigned) is drawn with thick lines. The white arrow indicates the position of the triangle
(grey) of (c); (c) Shown left is a triangle
(grey) and three adjacent triangles (white) connected to
through three facets. Shown in the square frame are all the possible values of the gradient of
and the adjacent triangles associated with the value. From left to right, a branch triangle, three regular triangles, three 2-fold singular triangles (terminal triangles), a 3-fold singular triangle (isolated triangle). Enclosed by a dotted circle is the gradient of
of (b).
where
. A subset of
is called a gradient of s.
Example 2. In Figure 1(b), a gradient (i.e., a set of edges) is assigned to each triangle of
. Most of the triangles are assigned one edge, some are assigned multiple edges, and others are assigned no edge. Shown in Figure 1(c) are all the possible values of the gradient of a triangle
of
, from which the encircled value is assigned to
in (b).
Let M be an n-simplex space. Let
and
. Two facets
and
of s which do not contain the edge e are defined by
where
means that the corresponding term is omitted.
Then, by definition, there are two n-simplices
and
such that
Definition 6 (Adjacent n-simplices A(s,G)). Let M be an n-simplex space. Let
and
. The adjacent n-simplices
associated with the edge e of s is defined by
where
and
are defined above. That is,
is the set of all the adjacent triangles of s which do not contain the edge e.
Let
be a gradient of s. The adjacent n-simplices
associated with G is defined by
In particular
.
Definition 7 (Local trajectory at an n-simplex). Let M be an n-simplex space. Let
and
. Let
. The local trajectory at s associated with the edge e is the sequence
of three consecutive n-simplices. Connecting these sequences together, we shall obtain a flow on M in Definition 12 and 13.
Example 3. Grey triangles in Figure 1(c) are the adjacent triangles
associated with the gradient G (thick lines) of
.
Conversely, a sequence
of three consecutive n-simplices determines uniquely an edge of the middle n-simplex s as follows.
Definition 8 (Tangent
). Let M be an n-simplex space. Let
be a sequence of three consecutive n-simplices of M, i.e.,
such that
. Let
The tangent
to
at s is an edge
of s, where
Note that
is not defined at singular simplices because singular simplices never occupy the middle position of a sequence of three consecutive n-simplices. (See Figure 1(c).)
Lemma 1. Let M be an n-simplex space. Let
and
. Let
be a sequence of three consecutive n-simplices of M. Then,
where
and
are the two n-simplices of
.
Proof. It follows immediately from the definition.
A differential structure is defined on an n-simplex space as follow.
Definition 9 (Tangent bundle
). Let M be an n-simplex space. The tangent bundle
of M is defined by
Definition 10 (Vector field V on M). Let M be an n-simplex space. A vector field V on M is a mapping which assigns to each n-simplex s of M, a gradient of s, i.e.,
where
denotes the power set of
. If
contains only one edge, s is called a regular n-simplex of V. Otherwise, s is called a singular n-simplex of V. If
, s is called a branch n-simplex of V. If
consists of m edges, s is called an m-fold singular n-simplex of V. If
has only one n-simplex, s is called a terminal n-simplex of V. If
, s is called an isolated n-simplex.
Example 4. Shown in Figure 1(b) is a vector field of the triangle space
of (a).
Definition 11 (Local trajectory of V on M). Let M be an n-simplex space and
. Let V be a vector field of M. Let
be a sequence of three consecutive n-simplices. Then,
is called a local trajectory of V at s if
Note that local trajectories may contain branch n-simplices.
Definition 12 (Trajectory of V on M). Let M be an n-simplex space. Let V be a vector field of M. Let
be a sequence of n-simplices, where I is either
,
,
, or
(
such that
). Then, L is called a trajectory of V if every consecutive three n-simplices of L is a local trajectory of V. i.e.,
A trajectory
of V is called closed if
are also local trajectories of V.
A trajectory L of V is called maximal if either L is closed, or
implies
for any trajectory
of V on M.
Definition 13 (Flow of V on M). Let M be an n-simplex space. Let V be a vector field of M. Let
be a set of maximal trajectories of V on M, where
if
. Then, L is called a flow of V on M if
Note that M is decomposed into a disjoint union of
if V has no branch triangle.
3.1.2. Two Functions on a Trajectory
Here we define two functions on trajectories of vector fields on an n-simplex space.
Definition 14 (U/D function g along a trajectory). Let M be an n-simplex space. Let V be a vector field of M. Let
(
) be a trajectory of V on M. An U/D function g along L is a
-valued function on L defined by
Example 5. Shown in Figure 2 is a trajectory
of the vector field of
given in Figure 1(b), where
. Then, we obtain an U/D function
along
as follows: Firstly, set
and move to the adjacent triangle
on the right. Then,
since
. In the same way, we obtain
. Now, let us move to
. Then,
since
. In the same way, we obtain
.
By considering the “integral along the trajectory” of a given U/D function, we shall obtain another function on the trajectory.
Definition 15 (Height function
on a trajectory). Let M be an n-simplex space. Let V be a vector field of M. Let
(
) be a trajectory of V on M. Let g be a U/D function along L. The height function
with respect to g is a
-valued function on L defined by
![]()
Figure 2. Two functions on a trajectory of triangles. Shown on the left is a trajectory
of the vector field of
given in Figure 1(b), where
. The table on the right shows the values of an U/D function along
and the height function on 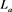 with respect to the U/D function.
with respect to the U/D function.
Example 6. Shown in Figure 2 is a trajectory  of the vector field of
of the vector field of  given in Figure 1(b), where
given in Figure 1(b), where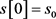 . The table on the right shows the values of an U/D function
. The table on the right shows the values of an U/D function 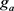 along
along 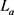 (See Example 5) and the height function
(See Example 5) and the height function  with respect to
with respect to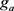 .
. 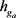 is obtained as follows: Firstly, set
is obtained as follows: Firstly, set . Since
. Since 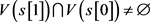 , we obtain
, we obtain . In the same way, we obtain
. In the same way, we obtain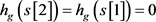 . Now, let us move to
. Now, let us move to . Then,
. Then, 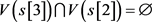 and
and

In the same way, we obtain![]() .
.
3.2. Flows of ![]() -Embeddable Vector Fileds
-Embeddable Vector Fileds
In general, n-simplex spaces consist of n-simplices of various shapes. Here, we shall consider a special class of n-simplex spaces consisting of n-simplices of the same shape.
3.2.1. ![]() -Embeddable Vector Fields of Triangles
-Embeddable Vector Fields of Triangles
Shown in Figure 3(a) is a triangle space ![]() obtained by partitioning
obtained by partitioning ![]() into triangles of the same shape. A vector field on
into triangles of the same shape. A vector field on ![]() is shown in Figure 3(b). In this case, the “two-dimensional” vector field of
is shown in Figure 3(b). In this case, the “two-dimensional” vector field of ![]() corresponds to a “three-dimensional” drawing on the surface of “mountains” of unit cubes of
corresponds to a “three-dimensional” drawing on the surface of “mountains” of unit cubes of ![]() as shown in Figure 3(c) and Figure 3(f). It is this type of vector fields of triangles that is considered in this section.
as shown in Figure 3(c) and Figure 3(f). It is this type of vector fields of triangles that is considered in this section.
Definition 16 (The three-dimensional lattice![]() ). Let
). Let ![]() be the three-dimensional lattice generated by three vectors
be the three-dimensional lattice generated by three vectors![]() ,
, ![]() , and
, and![]() , i.e.,
, i.e.,
![]()
Shown in Figure 3(d) is a unit cube of ![]() and its top view.
and its top view.
Definition 17 (The symmetric group ![]() on three letters). Let
on three letters). Let ![]() be the group of all the permutations of the set
be the group of all the permutations of the set![]() . Elements of
. Elements of ![]() are written in cyclic notation. For example, let
are written in cyclic notation. For example, let![]() . Then,
. Then, ![]() ,
, ![]() , and
, and![]() .
.
Definition 18 (The set B2 of all flat triangles). Let ![]() and
and![]() . The slant triangle
. The slant triangle ![]() is defined by
is defined by
![]()
where ![]() denotes the convex hull of three points
denotes the convex hull of three points ![]() (Definition 1). For example, the four slant triangles shown in Figure 3(e) are
(Definition 1). For example, the four slant triangles shown in Figure 3(e) are![]() ,
, ![]() ,
, ![]() , and
, and ![]() (from top to bottom).
(from top to bottom).
Let ![]() be the set of all slant triangles, i.e.,
be the set of all slant triangles, i.e.,
![]()
The shift operator ![]() on
on ![]() is defined by
is defined by
![]()
Then, an equivalence relation ![]() is defined on
is defined on ![]() by
by
![]() if and only if
if and only if ![]()
The ![]() -equivalence class of
-equivalence class of ![]() is called a flat triangle and denoted by
is called a flat triangle and denoted by![]() . For example, shown in Figure 3(e) is the
. For example, shown in Figure 3(e) is the ![]() -equivalence class of
-equivalence class of ![]() (
(![]() ).
).
The set of all flat triangles is denoted by![]() , i.e.,
, i.e.,
![]()
Lemma 2. ![]() is a triangle space (Definition 3).
is a triangle space (Definition 3).
Proof. It follows immediately from the definition.
By an abuse of notation, the “image on ![]() “ of an edge e of
“ of an edge e of ![]() is also denoted by
is also denoted by![]() . Note that
. Note that
![]()
where ![]() and
and ![]() (See Figure 3(e)). The tangent space
(See Figure 3(e)). The tangent space ![]() at
at ![]() (Definition 5) is given by
(Definition 5) is given by
![]()
where ![]() and
and![]() .
.
For simplicity, we often identify the edge ![]() with the monomial
with the monomial ![]() and we shall obtain a one-to-one correspondence
and we shall obtain a one-to-one correspondence
![]()
Definition 19 (Tangent bundle![]() ). The tangent bundle of
). The tangent bundle of ![]() (Definition 9) is given by
(Definition 9) is given by
![]()
Definition 20 (Gradient![]() ). Let
). Let![]() . The gradient
. The gradient ![]() of t is defined by
of t is defined by
![]()
That is, ![]() is a
is a ![]() -valued function on
-valued function on![]() . The “edge”
. The “edge” ![]() is also called the boundary edge of
is also called the boundary edge of![]() . (Strictly speaking,
. (Strictly speaking, ![]() is a set of one element. Here, we identify the set with its only element.)
is a set of one element. Here, we identify the set with its only element.)
Example 7. In Figure 3, the boundary edges ![]() are drawn with a thick line. For example, the boundary edge of
are drawn with a thick line. For example, the boundary edge of ![]() is
is ![]() (Figure 3(d)).
(Figure 3(d)).
Lemma 3. Let![]() . Then,
. Then,
![]()
That is, ![]() induces a
induces a ![]() -valued function on
-valued function on![]() . By an abuse of notation, the induced function is also denoted by
. By an abuse of notation, the induced function is also denoted by![]() , i.e.,
, i.e.,
![]()
Proof. By definition,
![]()
where![]() .
.
Lemma 4. Let![]() . Then, the local trajectory at
. Then, the local trajectory at ![]() associated with
associated with ![]() (Definition 7) is either
(Definition 7) is either
![]()
or
![]()
where
![]()
(See Figure 4(a)). The local trajectory is called the local trajectory associated with![]() .
.
Proof. Note that the two facets which do not contain the boundary edge ![]() are
are
![]()
(See above Definition 6). The result follows immediately.
Now, let us give the definition of “mountains of unit cubes” shown in Figure 3(c) and Figure 3(f).
Definition 21 (A tangent cone Cone A). Let A be a finite subset of![]() . A three-dimensional tangent cone
. A three-dimensional tangent cone ![]() is defined by
is defined by
![]()
The set of all the slant triangles on the surface of ![]() is denoted by
is denoted by ![]() , i.e.,
, i.e.,
![]()
Example 8. The tangent cone corresponding to the “mountains of unit cubes” of Figure 3(c) and Figure 3(f) is given by
![]()
where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
Lemma 5. Let ![]() be a tangent cone. Then,
be a tangent cone. Then,
![]()
where
![]()
Proof. For![]() ,
, ![]() s.t.
s.t.![]() . Then,
. Then, ![]() is the coordinate of p with respect to “origin” a. In particular,
is the coordinate of p with respect to “origin” a. In particular,
![]()
The result follows immediately.
The surface of a tangent cone induces a vector field of![]() .
.
Definition 22 (Vector field ![]() on
on![]() ). Let
). Let ![]() be a tangent cone. The vector field
be a tangent cone. The vector field ![]() on
on ![]() induced by c is defined by
induced by c is defined by
![]()
![]() is called a
is called a ![]() -embeddable vector field of triangles. Note that
-embeddable vector field of triangles. Note that ![]() has no singular triangle.
has no singular triangle.
Remark 1.![]() , and the value of
, and the value of ![]() is determined uniquely on
is determined uniquely on![]() .
.
Example 9. Shown in Figure 3(c) and Figure 3(f) is the vector field ![]() on
on ![]() induced by
induced by ![]() of Example 8.
of Example 8.
Local trajectories of ![]() on
on ![]() (Definition 11) is computed as follows.
(Definition 11) is computed as follows.
Lemma 6. Let![]() . Let
. Let ![]() be a tangent cone. Suppose that
be a tangent cone. Suppose that ![]() . Then, the local trajectory of
. Then, the local trajectory of ![]() at s is either
at s is either
![]()
or
![]()
where
![]()
Proof. See Lemma 4.
Lemma 7. Let![]() . Let
. Let ![]() be a tangent cone. Let
be a tangent cone. Let ![]() be the local trajectory of
be the local trajectory of ![]() at s. Then,
at s. Then,
![]()
Proof. Note that ![]() has no singular triangle on
has no singular triangle on![]() . The result follows immediately.
. The result follows immediately.
Proposition 1. Let V be a vector field on ![]() without singular triangles. Then,
without singular triangles. Then,
![]()
Proof. See [4].
3.2.2. The U/D and Height Functions Associated with ![]() -Embeddable Vector Fields
-Embeddable Vector Fields
Vector fields induced by a tangent cone are inherently associated with an U/D function and a height function.
Let![]() . Let
. Let ![]() be a tangent cone. Suppose that
be a tangent cone. Suppose that ![]() . Then, the local trajectory at s is either
. Then, the local trajectory at s is either ![]() or
or![]() , where
, where
![]()
(See Figure 4(a)).
Definition 23 (U/D function![]() ). Let
). Let![]() . Let
. Let ![]() be a tangent cone. Let
be a tangent cone. Let ![]() be the local trajectory of
be the local trajectory of ![]() at s (i.e.
at s (i.e.![]() ). The U/D function
). The U/D function ![]() at s along the trajectory associated with
at s along the trajectory associated with ![]() is defined by
is defined by
![]()
where ![]() and
and ![]() are given above. That is, −1 and +1 indicate “downhill” and “uphill” on the “mountain road”
are given above. That is, −1 and +1 indicate “downhill” and “uphill” on the “mountain road”![]() , respectively.
, respectively.
Remark 2. In Definition 14, U/D functions are not uniquely specified on an n-simplex space because the uphill and downhill along a trajectory are not given explicitly. On the other hand, the U/D function is uniquely specified on ![]() using the uphill and downhill along a trajectory of slant n-simplices.
using the uphill and downhill along a trajectory of slant n-simplices.
Lemma 8. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is an U/D function defined in Definition 14.
is an U/D function defined in Definition 14.
Proof. Let ![]() be a local trajectory of
be a local trajectory of![]() . Let
. Let ![]() and
and![]() . Suppose that
. Suppose that![]() . Then, either
. Then, either
![]()
or
![]()
Suppose that![]() . Then,
. Then, ![]() , where either
, where either
![]()
or
![]()
respectively. Since![]() , we obtain
, we obtain
![]()
That is,
![]()
Continuing in the same way for the other case, we obtain
![]()
The result follows immediately.
Proposition 2. Let ![]() be a tangent cone. Let
be a tangent cone. Let ![]() be a maximal trajectory of
be a maximal trajectory of ![]() on
on![]() . Let
. Let![]() . Then,
. Then,
![]()
Remark 3. The edge neighborhood ![]() consists of two triangles which share the boundary edge
consists of two triangles which share the boundary edge ![]() (Definition 4).
(Definition 4).
Proof. Let ![]() (
(![]() ). Suppose that
). Suppose that ![]() . Then, either
. Then, either ![]() or
or ![]() is enclosed by the trajectory
is enclosed by the trajectory ![]() of finite length, and the trajectory starting from the enclosed triangle (either
of finite length, and the trajectory starting from the enclosed triangle (either ![]() or
or ![]() ) has an “end point”. However,
) has an “end point”. However, ![]() has no singular triangle, which is a contradiction.
has no singular triangle, which is a contradiction.
Corollary 1. Suppose that L is closed. Then, the sum of ![]() over the “boundary” of L is equal to zero, i.e.,
over the “boundary” of L is equal to zero, i.e.,
![]()
where![]() .
.
Proof. Because of Proposition 2, the sum of ![]() over L is equal to the sum of
over L is equal to the sum of ![]() over the “boundary” of L, i.e.,
over the “boundary” of L, i.e.,
![]()
where![]() . Since the sum of
. Since the sum of ![]() over L is zero when L is closed, the result follows.
over L is zero when L is closed, the result follows.
Example 10. Shown in Figure 4(b) above is the value of the U/D function ![]() along a trajectory shown in Figure 3(b). The grey triangles belong to
along a trajectory shown in Figure 3(b). The grey triangles belong to![]() , and the white triangles belong to
, and the white triangles belong to![]() . The value of
. The value of ![]() on the first three triangles are
on the first three triangles are
![]()
Since
![]()
we obtain![]() . Since
. Since
![]()
we obtain![]() .
.
Note that two grey triangles sharing a thick edge have opposite values. The sum of the U/D function over the set of all the white triangles is equal to zero.
Definition 24 (Height function![]() ). The height function
). The height function ![]() on
on ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
The height function ![]() on
on ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
Let ![]() be a tangent cone. Then, the height function
be a tangent cone. Then, the height function ![]() on
on ![]() associated with
associated with ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
where![]() .
.
By an abuse of notation, we use the same name ![]() for three functions with different domains.
for three functions with different domains.
Lemma 9. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is a height function with respect to
is a height function with respect to ![]() defined in Definition 15.
defined in Definition 15.
Proof. Let ![]() be a local trajectory of
be a local trajectory of![]() . Then,
. Then, ![]() on
on ![]() is given by
is given by
![]()
The result follows immediately.
Proposition 3. Let![]() . Let
. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is constant on
is constant on![]() , i.e.,
, i.e.,
![]()
Proof. Since![]() , the result follows immediately.
, the result follows immediately.
Example 11. Shown in Figure 4(b) below is the value of the height function ![]() along a trajectory shown in Figure 3(b). The value of
along a trajectory shown in Figure 3(b). The value of ![]() on the first three triangles are
on the first three triangles are
![]()
where![]() ,
, ![]() ,
,![]() . Then,
. Then,
![]()
In the same way, we obtain![]() .
.
Note that two grey triangles sharing a thick edge have the same value.
3.2.3. ![]() -Embeddable Vector Fields of Tetrahedrons
-Embeddable Vector Fields of Tetrahedrons
This paper proposes a novel mathematical approach for the design of self-assembling molecules, where self-assembling molecules are represented as a union of trajectories of tetrahedrons. Here we shall consider vector fields on a tetrahedron space which are induced by a four-dimensional tangent cone.
In the same way as for the space ![]() of flat triangles, we shall define a “tetrahedron space” by partitioning
of flat triangles, we shall define a “tetrahedron space” by partitioning ![]() into tetrahedrons of the same shape. “Three-dimensional” vector fields of tetrahedrons then correspond to a “four-dimensional” drawing on the surface of “mountains” of unit cubes of
into tetrahedrons of the same shape. “Three-dimensional” vector fields of tetrahedrons then correspond to a “four-dimensional” drawing on the surface of “mountains” of unit cubes of![]() .
.
Definition 25 (The four-dimensional lattice![]() ). Let
). Let ![]() be the four-dimensional lattice generated by four vectors
be the four-dimensional lattice generated by four vectors![]() ,
, ![]() ,
, ![]() , and
, and![]() , i.e.,
, i.e.,
![]()
Shown in Figure 5(a) is a unit cube of ![]() and its “top view”.
and its “top view”.
Definition 26 (The symmetric group ![]() on four letters). Let
on four letters). Let ![]() be the group of all the permutations of the set
be the group of all the permutations of the set![]() . Elements of
. Elements of ![]() are written in cyclic notation. For example, let
are written in cyclic notation. For example, let![]() . Then,
. Then, ![]() ,
, ![]() ,
, ![]() , and
, and![]() .
.
Definition 27 (The set B3 of all flat tetrahedrons). Let ![]() and
and![]() . The slant tetrahedron
. The slant tetrahedron ![]() is defined by
is defined by
![]()
where ![]() denotes the convex hull of four points
denotes the convex hull of four points ![]() (Definition 1).
(Definition 1).
Let ![]() be the set of all slant tetrahedrons, i.e.,
be the set of all slant tetrahedrons, i.e.,
![]()
The shift operator ![]() on
on ![]() is defined by
is defined by
![]()
Then, an equivalence relation ![]() is defined on
is defined on ![]() by
by
![]()
![]()
Figure 5. Trajectory of tetrahedrons. (a) A unit cube of ![]() represented by the Schlegel diagram (bottom) and its projection on a three-dimensional hypersurface (top); (b) A facet of a unit cube of
represented by the Schlegel diagram (bottom) and its projection on a three-dimensional hypersurface (top); (b) A facet of a unit cube of ![]() (bottom) and its projection on a three-dimensional hyper-surface (top), where
(bottom) and its projection on a three-dimensional hyper-surface (top), where![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is the projected image of
is the projected image of![]() . The diagonal edge
. The diagonal edge ![]() is drawn with a thick line; (c) A tetrahedron and its six edges (thick lines). Edges are shown with the adjacent tetra-hedrons associated with them. Only four of them (left and center) are included in the tangent space; (d) A chain of isosceles tetrahedrons consisting four short edges and two long edges (length ratio is
is drawn with a thick line; (c) A tetrahedron and its six edges (thick lines). Edges are shown with the adjacent tetra-hedrons associated with them. Only four of them (left and center) are included in the tangent space; (d) A chain of isosceles tetrahedrons consisting four short edges and two long edges (length ratio is ![]() to 2), where tetrahedrons are connected via a long edge (left). By folding the chain of tetrahedrons, we shall obtain a trajectory of tetrahedrons (right). The boundary edges are drawn with thick lines; (e) Closed trajectories of the vector field on
to 2), where tetrahedrons are connected via a long edge (left). By folding the chain of tetrahedrons, we shall obtain a trajectory of tetrahedrons (right). The boundary edges are drawn with thick lines; (e) Closed trajectories of the vector field on ![]() induced by
induced by![]() , where
, where![]() . The boundary edges are drawn with thick lines.
. The boundary edges are drawn with thick lines.
The ![]() -equivalence class of
-equivalence class of ![]() is called a flat tetrahedron and denoted by
is called a flat tetrahedron and denoted by![]() .
.
The set of all flat tetrahedrons is denoted by![]() , i.e.,
, i.e.,
![]()
Example 12. The facet of a unit cube ![]() shown in Figure 5(b) bottom consists of six slant tetrahedrons
shown in Figure 5(b) bottom consists of six slant tetrahedrons
![]()
For example, ![]() is the tetrahedron
is the tetrahedron![]() . Then, the “projection image” of the facet is divided into six flat tetrahedrons (Figure 5(b) top)
. Then, the “projection image” of the facet is divided into six flat tetrahedrons (Figure 5(b) top)
![]()
Note that all the tetrahedrons share the “diagonal” edge![]() .
.
Lemma 10. ![]() is a tetrahedron space (Definition 3).
is a tetrahedron space (Definition 3).
Proof. It follows immediately from the definition.
By an abuse of notation, the “image on![]() ” of a k-face u of
” of a k-face u of ![]() is also denoted by
is also denoted by![]() . The tangent space
. The tangent space ![]() at
at ![]() (Definition 5) is then given by
(Definition 5) is then given by
![]()
where![]() ,
, ![]() and
and![]() .
.
For simplicity, we often identify the edge ![]() and
and ![]() with the monomial
with the monomial ![]() and
and![]() , respectively. Then, we shall obtain a one-to-one correspondence
, respectively. Then, we shall obtain a one-to-one correspondence
![]()
Definition 28 (Tangent bundle![]() ). The tangent bundle of
). The tangent bundle of ![]() (Definition 9) is given by
(Definition 9) is given by
![]()
Definition 29 (Gradient DSt). Let![]() . The gradient
. The gradient ![]() of t is defined by
of t is defined by
![]()
That is, ![]() is a
is a ![]() -valued function on
-valued function on![]() . In particular,
. In particular,
![]()
The “edge” ![]() is called the boundary edge of
is called the boundary edge of![]() . (Strictly speaking,
. (Strictly speaking, ![]() is a set of one element. Here, we identify the set with its only element.)
is a set of one element. Here, we identify the set with its only element.)
Example 13. Shown in Figure 5(c) is the flat tetrahedron ![]() (top) and its six edges (thick lines, bottom). All the six edges are shown with the adjacent tetrahedrons associated with them (Definition 6). Only four of them are included in the image of
(top) and its six edges (thick lines, bottom). All the six edges are shown with the adjacent tetrahedrons associated with them (Definition 6). Only four of them are included in the image of ![]() (left and center). Roughly speaking, U-turns are prohibited on
(left and center). Roughly speaking, U-turns are prohibited on ![]() (right).
(right).
Lemma 11. Let![]() . Then,
. Then,
![]()
That is, ![]() induces a
induces a ![]() -valued function on
-valued function on![]() . By an abuse of notation, the induced function is also denoted by
. By an abuse of notation, the induced function is also denoted by![]() , i.e.,
, i.e.,
![]()
Proof. It can be proved in the same way as the proof of Lemma 3.
Lemma 12. Let![]() . Then, the local trajectory at
. Then, the local trajectory at ![]() associated with
associated with ![]() (Definition 7) is
(Definition 7) is
![]()
or
![]()
where
![]()
The local trajectory is called the local trajectory associated with![]() .
.
Proof. Note that the two facets which do not contain the edge ![]() are
are
![]()
(See above Definition 6). The result follows immediately.
Example 14. Shown in Figure 5(d) (right) is a trajectory on ![]() obtained by patching overlapping local trajectories together. By connecting tetrahedrons
obtained by patching overlapping local trajectories together. By connecting tetrahedrons ![]() via edges
via edges ![]() and
and![]() , we shall obtain a chain of isosceles tetrahedrons as shown on the left. In the case of
, we shall obtain a chain of isosceles tetrahedrons as shown on the left. In the case of![]() , trajectories are obtained by folding the chain of tetrahedrons.
, trajectories are obtained by folding the chain of tetrahedrons.
Four-dimensional “mountains of unit cubes” is defined as follows.
Definition 30 (A tangent cone Cone A). Let A be a finite subset of![]() . A four-dimensional tangent cone
. A four-dimensional tangent cone ![]() is defined by
is defined by
![]()
The set of all the slant tetrahedrons on the surface of ![]() is denoted by
is denoted by![]() , i.e.,
, i.e.,
![]()
Lemma 13. Let ![]() be a tangent cone. Then,
be a tangent cone. Then,
![]()
where
![]()
Proof. It follows immediately from the definition.
The surface of a tangent cone induces a vector field of![]() .
.
Definition 31 (Vector field ![]() on
on![]() ). Let
). Let ![]() be a tangent cone. The vector field
be a tangent cone. The vector field ![]() on
on ![]() induced by c is defined by
induced by c is defined by
![]()
![]() is called a
is called a ![]() -embeddable vector field of tetrahedrons. Note that
-embeddable vector field of tetrahedrons. Note that ![]() has no singular tetrahedron.
has no singular tetrahedron.
Local trajectories of ![]() on
on ![]() (Definition 11) is computed as follows.
(Definition 11) is computed as follows.
Lemma 14. Let![]() . Let
. Let ![]() be a tangent cone. Suppose that
be a tangent cone. Suppose that ![]() . Then, the local trajectory of
. Then, the local trajectory of ![]() at s is either
at s is either
![]()
or
![]()
where
![]()
Proof. See Lemma 12.
Example 15. Shown in Figure 5(e) are four closed trajectories of the vector field ![]() on
on ![]() induced by
induced by
![]()
(The fourth trajectory is hidden behind others). A rhombic dodecahedron is divided into the set of four closed trajectories of length six.
There is no proof of the following claim.
Problem 1. Let V be a vector field on ![]() without singular tetrahedrons. Then, show that
without singular tetrahedrons. Then, show that
![]()
3.2.4. The U/D and Height Functions Associated with ![]() -Embeddable Vector Fields
-Embeddable Vector Fields
Vector fields induced by a tangent cone are inherently associated with an U/D function and a height function.
Definition 32 (U/D function![]() ). Let
). Let![]() . Let
. Let ![]() be a tangent cone. Let
be a tangent cone. Let ![]() be the local trajectory of
be the local trajectory of ![]() at s (i.e.
at s (i.e.![]() ). The U/D function
). The U/D function ![]() at s along the trajectory associated with
at s along the trajectory associated with ![]() is defined by
is defined by
![]()
where ![]() and
and ![]() are given in Lemma 14.
are given in Lemma 14.
Lemma 15. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is an U/D function defined in Definition 14.
is an U/D function defined in Definition 14.
Proof. It can be proved in the same way as the proof of Lemma 8.
There is no proof of the following two claims (See Proposition 2).
Problem 2. Let ![]() be a tangent cone. Let L be a maximal trajectory of
be a tangent cone. Let L be a maximal trajectory of ![]() on
on![]() . Let
. Let![]() . Then, show that
. Then, show that
![]()
Problem 3. Let ![]() be a tangent cone. Let L be a maximal trajectory of
be a tangent cone. Let L be a maximal trajectory of ![]() on
on![]() . Suppose that L is closed. Let
. Suppose that L is closed. Let![]() . Then, show that the sum of
. Then, show that the sum of ![]() over the “boundary” of L is equal to zero, i.e.,
over the “boundary” of L is equal to zero, i.e.,
![]()
where![]() .
.
Definition 33 (Height function![]() ). The height function
). The height function ![]() on
on ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
The height function ![]() on
on ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
Let ![]() be a tangent cone. Then, the height function
be a tangent cone. Then, the height function ![]() on
on ![]() associated with
associated with ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
where![]() .
.
By an abuse of notation, we use the same name ![]() for three functions with different domains.
for three functions with different domains.
Lemma 16. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is a height function with respect to
is a height function with respect to ![]() defined in Definition 15.
defined in Definition 15.
Proof. It can be proved in the same way as the proof of Lemma 9.
Proposition 4. Let![]() . Let
. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is constant on
is constant on![]() , i.e.,
, i.e.,
![]()
Proof. Since![]() , the result follows immediately.
, the result follows immediately.
3.2.5. ![]() -Embeddable Vector Fields of Line Segments
-Embeddable Vector Fields of Line Segments
Finally, let us consider briefly vector fields on a line segment space (Figure 6(a)) which are induced by a two-dimensional tangent cones. In the following section, vector fields of line segments will appear on the contour of a union of trajectories of triangles.
Definition 34 (The two-dimensional lattice![]() ). Let
). Let ![]() be the two-dimensional lattice generated by two vectors
be the two-dimensional lattice generated by two vectors ![]() and
and![]() , i.e.,
, i.e.,
![]()
Definition 35 (The symmetric group ![]() on two letters). Let
on two letters). Let ![]() be the group of all the permutations of the set
be the group of all the permutations of the set![]() .
. ![]() consists of an identity element and
consists of an identity element and![]() .
.
Definition 36 (The set B1 of all flat line segments). Let ![]() and
and![]() . The slant line segment
. The slant line segment ![]() is defined by
is defined by
![]()
Let ![]() be the set of all slant tetrahedrons, i.e.,
be the set of all slant tetrahedrons, i.e.,
![]()
The shift operator ![]() on
on ![]() is defined by
is defined by
![]()
Then, an equivalence relation ![]() is defined on
is defined on ![]() by
by
![]()
The ![]() -equivalence class of
-equivalence class of ![]() is called a flat line segment and denoted by
is called a flat line segment and denoted by![]() .
.
The set of all flat triangles is denoted by![]() , i.e.,
, i.e.,
![]()
Lemma 17. ![]() is a line segment space (Definition 3).
is a line segment space (Definition 3).
Proof. It follows immediately from the definition.
By an abuse of notation, the “image on![]() ” of a vertex v of
” of a vertex v of ![]() is also denoted by
is also denoted by![]() . The tangent space
. The tangent space ![]() at
at ![]() (Definition 5) is then given by
(Definition 5) is then given by
![]()
where![]() . For simplicity, we often identify the vertex
. For simplicity, we often identify the vertex ![]() with
with![]() . We shall then obtain a one-to-one correspondence
. We shall then obtain a one-to-one correspondence
![]()
Definition 37 (Tangent bundle![]() ). The tangent bundle of
). The tangent bundle of ![]() (Definition 9) is given by
(Definition 9) is given by
![]()
Definition 38 (Gradient![]() ). Let
). Let![]() . The gradient
. The gradient ![]() of t is defined by
of t is defined by
![]()
That is, ![]() is a
is a ![]() -valued function on
-valued function on![]() . The “vertex”
. The “vertex” ![]() is called the boundary vertex of
is called the boundary vertex of![]() . (Strictly speaking,
. (Strictly speaking, ![]() is a set of one element. Here, we identify the set with its only element.)
is a set of one element. Here, we identify the set with its only element.)
Example 16. Shown in Figure 6(b) are all the four types of gradients of line segments (Definition 5). In the case of![]() , only regular line segments are allowed.
, only regular line segments are allowed.
Lemma 18. Let![]() . Then,
. Then,
![]()
That is, ![]() induces a
induces a ![]() -valued function on
-valued function on![]() . By an abuse of notation, the induced function is also denoted by
. By an abuse of notation, the induced function is also denoted by![]() , i.e.,
, i.e.,
![]()
Proof. It can be proved in the same way as the proof of Lemma 3.
Lemma 19. Let![]() . Then, the local trajectory at
. Then, the local trajectory at ![]() associated with
associated with ![]() (Definition 7) is either
(Definition 7) is either
![]()
or
![]()
where![]() . The local trajectory is called the local trajectory associated with
. The local trajectory is called the local trajectory associated with![]() .
.
Proof. Note that ![]() is the only vertex of
is the only vertex of ![]() that is not the boundary vertex
that is not the boundary vertex![]() . Because of the boundary vertex
. Because of the boundary vertex ![]() between
between ![]() and
and![]() , local trajectories only go in one direction.
, local trajectories only go in one direction.
Two-dimensional “mountains of unit cubes” is defined as follows.
Definition 39 (A tangent cone Cone A). Let A be a finite subset of![]() . A two-dimensional tangent cone
. A two-dimensional tangent cone ![]() is defined by
is defined by
![]()
The set of all the slant line segments on the surface of ![]() is denoted by
is denoted by![]() , i.e.,
, i.e.,
![]()
The surface of a tangent cone induces a vector field of![]() .
.
Definition 40 (Vector field ![]() on
on![]() ). Let
). Let ![]() be a tangent cone. The vector field
be a tangent cone. The vector field ![]() on
on ![]() induced by c is defined by
induced by c is defined by
![]()
![]() is called a
is called a ![]() -embeddable vector field of line segments. Note that
-embeddable vector field of line segments. Note that ![]() has no singular line segment.
has no singular line segment.
Example 17. Shown in Figure 6(c) is a tangent cone
![]()
and the vector field on ![]() induced by the cone (top).
induced by the cone (top).
Local trajectories of ![]() on
on ![]() (Definition 11) is computed as follows.
(Definition 11) is computed as follows.
Lemma 20. Let![]() . Let
. Let ![]() be a tangent cone. Suppose that
be a tangent cone. Suppose that ![]() . Then, the local trajectory of
. Then, the local trajectory of ![]() at s is either
at s is either
![]()
Proof. See Lemma 19.
Example 18. Let us consider a trajectory ![]() of the vector filed
of the vector filed ![]() shown in Figure 6(c).
shown in Figure 6(c).
![]()
By connecting overlapping local trajectories, we shall obtain three maximal trajectories of line segments (Definition 12, 13), i.e.,
![]()
Proposition 5. Let V be a vector field on ![]() without singular line segments. Then,
without singular line segments. Then,
![]()
Proof. It follows immediately from the definition.
3.2.6. The U/D and Height Functions Associated with ![]() -Embeddable Vector Fields
-Embeddable Vector Fields
Vector fields induced by a tangent cone are inherently associated with an U/D function and a height function.
Definition 41 (U/D function![]() ). Let
). Let![]() . Let
. Let ![]() be a tangent cone. Let
be a tangent cone. Let ![]() be the local trajectory of
be the local trajectory of ![]() at s (i.e.
at s (i.e. ![]() or
or![]() ). The U/D function
). The U/D function ![]() at s along the trajectory associated with
at s along the trajectory associated with ![]() is defined by
is defined by
![]()
Lemma 21. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is an U/D function defined in Definition 14.
is an U/D function defined in Definition 14.
Proof. It follows immediately from the definition.
Example 19. Let us consider a flow ![]() of the vector filed
of the vector filed ![]() shown in Figure 6(c).
shown in Figure 6(c).
![]()
Definition 42 (Height function![]() ). The height function
). The height function ![]() on
on ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
The height function ![]() on
on ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
Let ![]() be a tangent cone. Then, the height function
be a tangent cone. Then, the height function ![]() on
on ![]() associated with
associated with ![]() is a
is a ![]() -valued function defined by
-valued function defined by
![]()
where![]() .
.
By an abuse of notation, we use the same name ![]() for three functions with different domains.
for three functions with different domains.
Lemma 22. Let ![]() be a tangent cone. Then,
be a tangent cone. Then, ![]() is a height function with respect to
is a height function with respect to ![]() defined in Definition 15.
defined in Definition 15.
Proof. It follows immediately from the definition.
Example 20. Let us consider a flow ![]() of the vector filed
of the vector filed ![]() shown in Figure 6(c). Suppose that
shown in Figure 6(c). Suppose that![]() . Then,
. Then,
![]()
3.3. Flows of Locally ![]() -Embeddable Vector Fileds
-Embeddable Vector Fileds
In our mathematical model of self-assembling molecules, the “spatial arrangement of the subunits (such as amino acids, nucleic acids, or others)” on their surfaces corresponds to the “flow of triangles” induced on the surface of a union of trajectories of tetrahedrons. Surface flows (i.e., flows of triangles) on trajectories of tetrahedrons of ![]() -embeddable vector fields are not necessarily
-embeddable vector fields are not necessarily ![]() -embeddable. Here, we shall consider vector fields of n-simplices that is locally isomorphic to a
-embeddable. Here, we shall consider vector fields of n-simplices that is locally isomorphic to a ![]() -embeddable vector field.
-embeddable vector field.
In the previos paper [5], we have proposed the ![]() -embeddability as a novel geometrical interpretation of the long-distance regulation of protein interactions such as “allosteric regulation”. (See the self-eclipsed closed trajectory shown in Example 26.)
-embeddability as a novel geometrical interpretation of the long-distance regulation of protein interactions such as “allosteric regulation”. (See the self-eclipsed closed trajectory shown in Example 26.)
Let M be an n-simplex space and![]() . Let
. Let ![]() be the set of all the k-faces (
be the set of all the k-faces (![]() ) of n-simplices of U, i.e.,
) of n-simplices of U, i.e.,
![]()
where ![]() is the set of all the k-faces of s (Definition 2).
is the set of all the k-faces of s (Definition 2).
Definition 43 (Simplical isomorphism). Let ![]() and
and ![]() be n-simplex spaces. Let
be n-simplex spaces. Let ![]() and
and![]() . A one-to-one mapping
. A one-to-one mapping ![]() from
from ![]() to
to ![]() is called a simplical isomorphism on
is called a simplical isomorphism on ![]() if
if
![]()
for each k-face ![]()
![]() of
of![]() . Then,
. Then, ![]() is called simplically isomorphic to
is called simplically isomorphic to ![]() by
by![]() . This is denoted by writing
. This is denoted by writing![]() .
.
Definition 44 (n-cube neighborhood). An n-cube neighborhood of ![]() is a set of n-simplices expressed in the form of
is a set of n-simplices expressed in the form of
![]()
where![]() . As shown in Figure 7, a 1-cube neighborhood is an interval composed of two flat line segments, a 2-cube neighborhood is a hexagonal region composed of six flat triangles, and a 3-cube neighborhood is a dodecahedronal region composed of 24 flat tetrahedrons.
. As shown in Figure 7, a 1-cube neighborhood is an interval composed of two flat line segments, a 2-cube neighborhood is a hexagonal region composed of six flat triangles, and a 3-cube neighborhood is a dodecahedronal region composed of 24 flat tetrahedrons.
Let U be a subset of an n-simplex space M. U is called an n-cube neighborhood of M if there exist an n-cube neighborhood ![]() and a simplical isomorphism
and a simplical isomorphism ![]() on U such that
on U such that
![]()
Definition 45 (Locally Bn-embeddable n-simplex space). Let M be an n-simplex space and![]() . W is called locally
. W is called locally ![]() -embeddable if each
-embeddable if each ![]() has an n-cube neighborhood
has an n-cube neighborhood![]() , i.e.,
, i.e.,
![]()
where ![]() is a simplical isomorphism on U.
is a simplical isomorphism on U.
Definition 46 (Locally ![]() -embeddable vector field on an n-cube neighborhood U). Let M be a locally
-embeddable vector field on an n-cube neighborhood U). Let M be a locally ![]() -embeddable n-simplex space and
-embeddable n-simplex space and![]() . Let
. Let ![]() and
and ![]() be n-cube neighborhoods such that
be n-cube neighborhoods such that![]() , where
, where ![]() is a simplical isomorphism on U. Let V be a vector field on W. Then, V is called locally
is a simplical isomorphism on U. Let V be a vector field on W. Then, V is called locally ![]() -embeddable on U if there exist a one-to-one mapping
-embeddable on U if there exist a one-to-one mapping ![]() and a tangent cone
and a tangent cone ![]() such that
such that
![]()
where![]() ,
, ![]() , and
, and ![]() is the vector field on
is the vector field on ![]() induced by c. This is denoted by writing
induced by c. This is denoted by writing![]() .
. ![]() is called a local
is called a local ![]() -embedding of TM on U.
-embedding of TM on U.
Definition 47 (Locally ![]() -embeddable vector field on a subset W). Let M be a locally
-embeddable vector field on a subset W). Let M be a locally ![]() -embeddable n-simplex space and
-embeddable n-simplex space and![]() . Let V be a vector field on M. Then, V is called locally
. Let V be a vector field on M. Then, V is called locally ![]() -embeddable on W if, for
-embeddable on W if, for![]() ,
,
![]()
![]()
Figure 7. n-cube neighborhood. (a) A 1-cube neighborhood (left). Vector fields induced by a tangent cone on the interval are shown on the right. Arrows indicate the position of boundary vertices; (b) A 2-cube neighborhood (left). Vector fields induced by a tangent cone on the hexagonal region are shown on the right. Boundary edges are drawn with thick lines; (c) A 3-cube neighborhood consisting of 24 tetrahedrons.
where ![]() is a simplical isomorphism on U,
is a simplical isomorphism on U, ![]() is the vector field on
is the vector field on ![]() induced by c, and
induced by c, and ![]() is a local
is a local ![]() -embedding of TM on U.
-embedding of TM on U.
Definition 48 (U/D function and height function). Let M be a locally ![]() -embeddable n-simplex space and
-embeddable n-simplex space and![]() . Let V be a locally
. Let V be a locally ![]() -embeddable vector field on W. Let
-embeddable vector field on W. Let ![]() and
and ![]() be an n-cube neighborhood of s. We can then define an U/D function and a height function on
be an n-cube neighborhood of s. We can then define an U/D function and a height function on![]() .
.
By patching height functions on ![]() (
(![]() ) seamlessly over W, we shall obtain either a singlevalued or a multivalued height function on W which is called the continuation of the local height functions (i.e., height functions on
) seamlessly over W, we shall obtain either a singlevalued or a multivalued height function on W which is called the continuation of the local height functions (i.e., height functions on![]() ) to W. The continuation of height functions to W is called a height function on W.
) to W. The continuation of height functions to W is called a height function on W.
By patching U/D functions on ![]() (
(![]() ) consistently over W, we shall obtain a singlevalued U/D function on W which is called the continuation of the local U/D functions to W. The continuation of U/D functions to W is called a U/D function on W.
) consistently over W, we shall obtain a singlevalued U/D function on W which is called the continuation of the local U/D functions to W. The continuation of U/D functions to W is called a U/D function on W.
There is no proof of the following claim.
Problem 4. Let V be a locally ![]() -embeddable vector field on
-embeddable vector field on![]() . Let
. Let ![]() be a closed trajectory of V. Let g be an U/D function along L. Let
be a closed trajectory of V. Let g be an U/D function along L. Let ![]() be the height function with respect to g. Then, show that
be the height function with respect to g. Then, show that
![]()
Example 21 (The Penrose stairs-like closed trajectory [25] ). Shown in Figure 8(a) is a locally ![]() -embeddable vector fields of triangles. Note that each triangle except the isolated triangle (white) has one of the 2-cube neighborhoods shown in Figure 7(b). Shown on the right is the closed trajectory around the isolated triangle:
-embeddable vector fields of triangles. Note that each triangle except the isolated triangle (white) has one of the 2-cube neighborhoods shown in Figure 7(b). Shown on the right is the closed trajectory around the isolated triangle:![]() ,
, ![]() ,
, ![]() ,
, ![]() . Starting from the slant triangle
. Starting from the slant triangle![]() , an U/D function and a height function are computed as shown at the bottom. Returning to the initial triangle, we shall obtain a slant triangle
, an U/D function and a height function are computed as shown at the bottom. Returning to the initial triangle, we shall obtain a slant triangle ![]() over
over ![]() . That is, going around the trajectory increases the value of the height function by 6.
. That is, going around the trajectory increases the value of the height function by 6.
Example 22 (A four-dimensional version of the Penrose stairs). Shown in Figure 8(b) is a closed trajectory on a locally ![]() -embeddable vector fields of tetrahedrons. The trajectory goes around a 4-fold singular tetrahedron (Definition 10):
-embeddable vector fields of tetrahedrons. The trajectory goes around a 4-fold singular tetrahedron (Definition 10):![]() ,
, ![]() ,
, ![]() ,
, ![]() . Start from the slant tetrahedron
. Start from the slant tetrahedron ![]() and go around the trajectory clockwise, we shall obtain a slant triangle
and go around the trajectory clockwise, we shall obtain a slant triangle ![]() over
over ![]() when returning to the initial tetrahedron. That is, going around the trajectory increases the value of the height function by 12.
when returning to the initial tetrahedron. That is, going around the trajectory increases the value of the height function by 12.
Example 23 (A helix of tetrahedrons). Shown in Figure 8(c) is a trajectory on a locally ![]() -embeddable vector fields of tetrahedrons. The trajectory goes around a 3-fold singular tetrahedron (Definition 10) clockwise helically:
-embeddable vector fields of tetrahedrons. The trajectory goes around a 3-fold singular tetrahedron (Definition 10) clockwise helically: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
4. Boundary Value Problem
Now let us consider the design problem of self-assembling molecules using the mathematical framework described in the previous section. In particular, we shall consider the problem of finding a backbone conformation that forms a shape of the desired properties. In our model, the question is rephrased as a “boundary value problem for flows on a space of 3-simplices”, i.e.,
“Given a triangular flow (i.e., desired properties). Find a tetrahedral flow (i.e., well-defined shape) that induces the triangular flow as its surface flow.”
After giving the definition of surface flow in 4.1, we shall consider the boundary value problem in some simple cases in 4.2. We shall also characterize ![]() -embeddable surface flow (Proposition 8) and locally
-embeddable surface flow (Proposition 8) and locally ![]() -embeddable surface flow (Problem 5) using U/D functions.
-embeddable surface flow (Problem 5) using U/D functions.
In 4.3, we shall propose algebraic representations of ![]() -embeddabe surface flow (Proposition 9) and locally
-embeddabe surface flow (Proposition 9) and locally ![]() -embeddabe surface flow (Problem 6) using cotangent cones (Definition 53, 54). We believe they will give a kind of geometrical characterization of “allosteric proteins” as described in [5].
-embeddabe surface flow (Problem 6) using cotangent cones (Definition 53, 54). We believe they will give a kind of geometrical characterization of “allosteric proteins” as described in [5].
4.1. Surface Flow
Definition 49 (The surface ![]() of L). Let V be a vector field of an n-simplex space M (
of L). Let V be a vector field of an n-simplex space M (![]() ). Let
). Let ![]() be a union of trajectories of V. A facet u of
be a union of trajectories of V. A facet u of ![]() is called a boundary facet of L if the facet neighborhood
is called a boundary facet of L if the facet neighborhood ![]() (Definition 4). The surface
(Definition 4). The surface ![]() of L is the set of all boundary facets of L, i.e.,
of L is the set of all boundary facets of L, i.e.,
![]()
That is, ![]() is the
is the ![]() -dimensional surface of the n-dimensional region swept by L.
-dimensional surface of the n-dimensional region swept by L.
The surface of a union of maximal trajectories of n-simplices is actually an ![]() -simplex space. That is, each
-simplex space. That is, each ![]() -simplex on the surface is connected uniquely to n adjacent
-simplex on the surface is connected uniquely to n adjacent ![]() -simplices on the surface through its n facets (Definition 3).
-simplices on the surface through its n facets (Definition 3).
Proposition 6. Let V be a vector field of an n-simplex space M (![]() ). Let
). Let ![]() be a union of maximal trajectories of V. Then,
be a union of maximal trajectories of V. Then, ![]() is an
is an ![]() -simplex space.
-simplex space.
Proof. We shall show that, for any ![]() and any facet
and any facet![]() , there is a unique adjacent
, there is a unique adjacent ![]() -simplex of
-simplex of ![]() connecting to u through w.
connecting to u through w.
Let![]() . Then, by definition,
. Then, by definition,
![]()
Let ![]() be a facet. Then,
be a facet. Then, ![]() is divided into two subsets
is divided into two subsets ![]() and
and ![]() by
by ![]() and
and
![]()
Let ![]() be the facet such that
be the facet such that![]() . If
. If![]() , then
, then ![]() and
and ![]() gives an
gives an ![]() -simplex connecting to u through w.
-simplex connecting to u through w.
Otherwise, there exists an adjacent n-simplex ![]() of
of ![]() such that
such that
![]()
Let ![]() be the facet such that
be the facet such that![]() . If
. If![]() , then
, then ![]() and
and ![]() gives an
gives an ![]() -simplex connecting to u through w.
-simplex connecting to u through w.
Otherwise, continuing in the same way, we will obtain an ![]() -simplex connecting to u through w because the finite set
-simplex connecting to u through w because the finite set ![]() is divided into two subsets by
is divided into two subsets by![]() .
.
Note that ![]() and
and ![]() may consist of multiple consecutive parts, i.e., u may have multiple
may consist of multiple consecutive parts, i.e., u may have multiple ![]() -simplices connecting through w. However, the “adjacent
-simplices connecting through w. However, the “adjacent ![]() -simplex on the surface” of u is uniquely determined.
-simplex on the surface” of u is uniquely determined.
A union of maximal trajectories of n-simplices induces a flow of ![]() -simplices on its surface that is an
-simplices on its surface that is an ![]() -simplex space.
-simplex space.
Proposition 7. Let V be a vector field of an n-simplex space M (![]() ). Let
). Let ![]() be a union of maximal trajectories of V. Set
be a union of maximal trajectories of V. Set
![]()
![]() then induces a vector field on
then induces a vector field on![]() . We denote the induced vector field by
. We denote the induced vector field by![]() .
.
Let![]() . Note that
. Note that ![]() consists of an n-simplex by definition. We then have
consists of an n-simplex by definition. We then have
![]()
If V has no singular n-simplices, then ![]() has no singular
has no singular ![]() -simplices neither.
-simplices neither.
Proof. It follows immediately from the definition. See the following remark.
Remark 4. Recall that ![]() is a subset of the set
is a subset of the set ![]() of all the edges of
of all the edges of ![]() (Definition 5, 10). s is a regular n-simplex of V if
(Definition 5, 10). s is a regular n-simplex of V if ![]() contains only one edge. Otherwise, s is called a singular n-simplex of V.
contains only one edge. Otherwise, s is called a singular n-simplex of V.
Example 24 (Surface flow of line segments). Shown in Figure 9(a) are a closed trajectory (right) and a union of closed trajectories (left) of![]() . The same surface flow shown in Figure 9(b) is induced on their surfaces. In other words, the surface flow dose not specify uniquely a region (i.e., a union of trajectories of triangles) of
. The same surface flow shown in Figure 9(b) is induced on their surfaces. In other words, the surface flow dose not specify uniquely a region (i.e., a union of trajectories of triangles) of![]() .
.
Shown in Figure 9(c) is a union of closed trajectories of![]() , which induces the surface flow shown in Figure 9(d). In this case, the surface flow specifies uniquely a region of
, which induces the surface flow shown in Figure 9(d). In this case, the surface flow specifies uniquely a region of![]() .
.
Both of the surface flows are locally ![]() embeddable. (They are not
embeddable. (They are not ![]() embeddable because they are defined on a “closed curve”.)
embeddable because they are defined on a “closed curve”.)
4.2. Boundary Value Problem
The definition of the boundary value problem for flows on a space of n-simplices is given as follows.
Definition 50 (Boundary value problem for flows on a space of n-simplices). Let A be an ![]() -simplex space. Let M be an n-simplex space. Given a flow E of a vector field
-simplex space. Let M be an n-simplex space. Given a flow E of a vector field ![]() on A. Find a union L of trajectories of a vector field V on M such that
on A. Find a union L of trajectories of a vector field V on M such that
![]()
where![]() ,
, ![]() , and
, and ![]() denotes a simplical isomorphism between A and B (Definition 43).
denotes a simplical isomorphism between A and B (Definition 43).
Definition 51 (Locally ![]() -embeddable surface flow of
-embeddable surface flow of ![]() -simplices). Let A be an
-simplices). Let A be an ![]() -simplex space. Let E be a flow of a vector field on A. E is called locally
-simplex space. Let E be a flow of a vector field on A. E is called locally ![]() -embeddable if the pair
-embeddable if the pair ![]() has a solution
has a solution ![]() to the boundary value problem defined in Definition 50 such that V is locally
to the boundary value problem defined in Definition 50 such that V is locally ![]() -embeddable on
-embeddable on![]() . E is called
. E is called ![]() -embeddable if V is
-embeddable if V is ![]() -embeddable on
-embeddable on![]() .
.
Example 25 (Boundary value problem for flows on a space of triangles). Suppose that we are given a flow of line segments shown in Figure 9(b). That is, the A of Definition 50 is a “closed curve” of line segments of length 16, and the E of Definition 50 is a flow of a locally ![]() -embeddable vector field on A.
-embeddable vector field on A.
Then, we have two solutions on ![]() shown in Figure 9(a). One is a trajectory of a
shown in Figure 9(a). One is a trajectory of a ![]() embeddable vector field on
embeddable vector field on ![]() (left). The other is a union of two closed trajectories of another
(left). The other is a union of two closed trajectories of another ![]() -embeddable vector field on
-embeddable vector field on ![]() (right). In particular, E is
(right). In particular, E is ![]() -embeddable.
-embeddable.
On the other hand, suppose that we are given a flow of line segments shown in Figure 9(d). That is, A is a “closed curve” of line segments of length 16, and E is a flow of another locally ![]() -embeddable vector field on A.
-embeddable vector field on A.
Then, a solution is determined uniquely on ![]() (Figure 9(c)), and E is also
(Figure 9(c)), and E is also ![]() -embeddable.
-embeddable.
Proposition 8. Let A be a line segment space. Let E be a flow of a vector field on A. That is, ![]() is the pair given in Definition 50. Let g be the (continuation of) U/D function on A (Definition 41, 48). Then,
is the pair given in Definition 50. Let g be the (continuation of) U/D function on A (Definition 41, 48). Then,
![]()
Proof. It follows immediately from Corollary 1 after Proposition 2.
Remark 5. The claim of opposite direction is not valid. That is,
![]()
For a counterexample, see Example 26.
Example 26 (Self-eclipsed closed trajectory of triangles). Suppose that we are given a flow of line segments shown in Figure 10(a). That is, the A of Definition 50 is a loop of line segments of length 10, and the E of Definition 50 is a flow of a locally ![]() -embeddable vector field on A.
-embeddable vector field on A.
Then, we have a solution on ![]() shown in Figure 10(b), which is a trajectory of a
shown in Figure 10(b), which is a trajectory of a ![]() -embeddable vector field on
-embeddable vector field on![]() . That is, E is
. That is, E is ![]() -embeddable. Note that the “slope” of the line segment
-embeddable. Note that the “slope” of the line segment ![]() is under the influence of another line segment
is under the influence of another line segment![]() . (That is, the region swept by the closed trajectory of triangles is “eclipsed by itself” at
. (That is, the region swept by the closed trajectory of triangles is “eclipsed by itself” at ![]() and
and![]() . See [5] for detailed description.)
. See [5] for detailed description.)
On the other hand, suppose that we are given a flow of line segments shown in Figure 10(c). That is, A is a loop of line segments of length 10, and E is a flow of another locally ![]() -embeddable vector field on A.
-embeddable vector field on A.
Then, we have a solution on ![]() shown in Figure 10(d), which is a trajectory of a locally
shown in Figure 10(d), which is a trajectory of a locally ![]() -embeddable vector field on
-embeddable vector field on![]() . That is, E is locally
. That is, E is locally ![]() -embeddable. In this case, height functions are not multivalued (Definition 48) on the surface flow, but the “slope” of the line segments
-embeddable. In this case, height functions are not multivalued (Definition 48) on the surface flow, but the “slope” of the line segments ![]() and
and ![]() are not consistent.
are not consistent.
There is no proof of the following claim.
Problem 5. Let A be a line segment space. Let E be a flow of a vector field on A. That is, ![]() is the pair given in Definition 50. Let g be the (continuation of) U/D function on A (Definition 41, 48). Then, show that
is the pair given in Definition 50. Let g be the (continuation of) U/D function on A (Definition 41, 48). Then, show that
![]()
Remark 6. The claim of opposite direction is not valid. That is,
![]()
For a counterexample, see Example 27.
Example 27 (Closed trajectory around a singular n-simplex). Let A be a loop of line segments of length 9. Let E be the (outer) surface flow E induced by the closed trajectory of triangles of Figure 8(a) right. Then,
![]()
(Recall that it is a version of Penrose stirs.)
In this case, we shall obtain a solution (to the boundary value problem) on a triangle space if we permit a singular triangle as shown in Figure 8(a). In particular, E is locally ![]() -embeddable.
-embeddable.
4.3. The Cotangent Cone Representation of ![]()
So far we have considered two types of surface flows of ![]() -simplices. One is
-simplices. One is ![]() -embeddable, and the other is locally
-embeddable, and the other is locally ![]() -embeddable. In the case of
-embeddable. In the case of![]() , it may be possible to distinguish between the two types using “cotangent” cones (Definition 53, 54) as shown below. For the case of
, it may be possible to distinguish between the two types using “cotangent” cones (Definition 53, 54) as shown below. For the case of![]() , see [5].
, see [5].
First, let us consider the lattice generated by gradients (Definition 20) of slant n-simplices of![]() .
.
Definition 52 (The three-dimensional conjugate lattice![]() ). Let
). Let ![]() be the three-dimensional lattice generated by three vectors
be the three-dimensional lattice generated by three vectors![]() ,
, ![]() , and
, and![]() , i.e.,
, i.e.,
![]()
(Figure 11(a)). ![]() is called the three-dimensional conjugate lattice.
is called the three-dimensional conjugate lattice.
Two types of cotangent cones are defined on![]() .
.
Definition 53 (A cotangent cone![]() ). Let A be a finite subset of
). Let A be a finite subset of![]() . A three-dimensional cotangent cone
. A three-dimensional cotangent cone ![]() is defined by
is defined by
![]()
Example 28. Shown in Figure 11(b) are a tangent cone and a cotangent cone:
![]()
Note that the surface flow of Figure 10(a) is obtained as the intersection
![]()
That is, the intersection of a tangent cone and a cotangent cone gives a ![]() -embeddable surface flow.
-embeddable surface flow.
Definition 54 (An inverted cotangent cone![]() ). Let A be a finite subset of
). Let A be a finite subset of![]() . A three-dimensional inverted cotangent cone
. A three-dimensional inverted cotangent cone ![]() is defined by
is defined by
![]()
Example 29. Shown in Figure 11(c) are a cotangent cone and an inverted cotangent cone:
![]()
Note that the surface flow of Figure 10(c) is obtained as the intersection
![]()
That is, the intersection of a cotangent cone and an inverted cotangent cone gives a locally ![]() -embeddable surface flow.
-embeddable surface flow.
![]() -embeddable surface flows are characterize by the following proposition.
-embeddable surface flows are characterize by the following proposition.
Proposition 9. Let E be a surface flow of line segments on a closed curve. Then, E is ![]() -embeddable if and only if E is obtained as the intersection of a tangent cone and a cotangent cone (See Figure 11(b)). That is,
-embeddable if and only if E is obtained as the intersection of a tangent cone and a cotangent cone (See Figure 11(b)). That is,
![]()
Proof. (![]() ) It follows immediately from the definition.
) It follows immediately from the definition.
(![]() ) The contour of the region swept by a union of closed trajectories of a
) The contour of the region swept by a union of closed trajectories of a ![]() -embeddable vector field
-embeddable vector field ![]() (c is a tangent cone) is obtained as a intersection of a tangent cone c and a cotangent cone. See [5] for detailed description.
(c is a tangent cone) is obtained as a intersection of a tangent cone c and a cotangent cone. See [5] for detailed description.
In the case of locally ![]() -embeddable surface flows, we have the following claim. (There is no proof of the claim.)
-embeddable surface flows, we have the following claim. (There is no proof of the claim.)
Problem 6. Let E be a surface flow of line segments on a closed curve. Suppose that height functions are not multivalued along the closed curve (Definition 48). Show that E is locally ![]() -embeddable if and only if E is obtained as the intersection of a cotangent cone and an inverted cotangent cone (See Figure 11(c)). That is,
-embeddable if and only if E is obtained as the intersection of a cotangent cone and an inverted cotangent cone (See Figure 11(c)). That is,
![]()
5. Conclusions
After an introduction to the discrete differential geometry of n-simplices, we gave a few considerations to the boundary value problem for flows on a space of n-simplices. Although the boundary value problem is considered with the design of self-assembling molecules in mind, there are still many challenges in practical application.
One of the challenges is how to describe flows (i.e., desired properties) on the boundary surface. Note that the shape of the closed surface is not given explicitly. It is not obvious how to describe flows on a closed surface without a specific shape. In addition, from the viewpoint of molecular design, it may be excessive to specify a flow over the entire surface. For example, it is a set of geometric constraints around the active sites that is considered in protein design. Furthermore, we don’t even know how many types of flows of ![]() -simplices are allowed on the surface of a union of trajectories of n-simplices.
-simplices are allowed on the surface of a union of trajectories of n-simplices.
However, it should be possible to find an approach for application. Examples include the characterization of two types of surface flows discussed at the end of this paper, i.e., ![]() -embeddable ones and locally
-embeddable ones and locally ![]() -embeddable ones. It is a rough classification of surface flows, but may be essential in characterizing important properties of biomolecules such as allosteric regulation.
-embeddable ones. It is a rough classification of surface flows, but may be essential in characterizing important properties of biomolecules such as allosteric regulation.
Finally, the ultimate goal of the research is a mathematical description of the shape of proteins. The description of shapes is important because the function of a protein (i.e., protein-protein interactions) is determined by its shape. The author is considering two approaches: an implicit one and an explicit one.
The implicit approach considers an algebraic description (or “simultaneous equations”) of protein-protein interactions. The shape of proteins is then obtained as a semantics of the description (or “a solution set” of the equations). That is, the author thinks that the shape of proteins forms a kind of “number system”, and has proposed a system of “hetero numbers” elsewhere.
On the other hand, the explicit approach directly considers a geometrical description of the shape of proteins. This paper takes the explicit approach and geometrically considers the shape of closed trajectories of n-simplices. Unlike the continuum counterpart, a sphere has several triangular surface flows without singular triangles. Using the results of this paper, the classification of the shape of closed trajectories can be reduced to the classification of their surface flows.
We believe this paper not only provides a new perspective to identify the underlying general principles of self-assembling molecules, but also promotes further collaboration between mathematics and other disciplines in life science.