Modulus-Based Matrix Splitting Iteration Methods for a Class of Stochastic Linear Complementarity Problem

Qianqian Lu, Chenliang Li

School of Mathematics and Computing Science, Guangxi Colleges and Universities Key Laboratory of Data Analysis and Computation, Guilin University of Electronic Technology, Guilin, China.

DOI: 10.4236/ajor.2019.96016                

Abstract

For the expected value formulation of stochastic linear complementarity problem, we establish modulus-based matrix splitting iteration methods. The convergence of the new methods is discussed when the coefficient matrix is a positive definite matrix or a positive semi-definite matrix, respectively. The advantages of the new methods are that they can solve the large scale stochastic linear complementarity problem, and spend less computational time. Numerical results show that the new methods are efficient and suitable for solving the large scale problems.

Keywords

Stochastic Linear Complementarity Problem, Modulus-Based Matrix Splitting, Expected Value Formulation, Positive Semi-Definite Matrix

1. Introduction

The complementarity problems have been widely used in the engineering design, information technology, economic equilibrium, etc. Since some elements may involve uncertain data in practical applications, many problems can be attributed to stochastic variational inequality problems or stochastic linear complementarity problems, and arouse the attention of many researchers. Gurkan et al. [1] proposed the expected value (EV) formulation of stochastic variational inequality by using the sample-path method. Chen and Fukushima [2] proposed the expected residual minimization (ERM) formulation for stochastic linear complementarity problems by quasi-Monte Carlo methods. Lin and Fukushima [3] proposed the stochastic mathematical programs with equilibrium constraints (SMPEC) for the stochastic nonlinear complementarity problems. Zhou and Cacceta [4] transformed the monotone stochastic linear complementarity problem (SLCP) in finite sample space into a constrained minimization problem, and solved it with the Feasible Semi-smooth Newton Method. Mangasarian and Ren [5] given a new error bound for the monotone LCP based on the error bounds. Chen et al. [6] studied the SLCP involving a random matrix whose expectation matrix is positive semi-definite. Zhang and Chen [7] proposed a smooth projection gradient algorithm to solve the SLCP. However, these methods are only suitable for solving the small-scale SLCP.

In recent years, some scholars have proposed a series of methods for the study of large-scale complementarity problems. Dong and Jiang [8] proposed a class of modified modulus-based method. Bai [9] presented a class of modulus-based matrix splitting iteration methods. Bai and Evans [10] [11] also proposed a class of modulus-based synchronous multi-splitting (MSM) iteration methods. Bai and Zhang [12] further proposed a synchronous two-stage multi-splitting iteration method, which can be applied to solving the large-scale linear complementarity problems. Zhang [13] summarized the latest development and achievements of the modulus-based matrix splitting iteration methods, including the corresponding multi-splitting iteration methods, etc. Zhang [14] improved the convergence theorem of matrix multi-splitting methods for linear complementarity problems. Such methods are easy to be implemented and very efficient in practical applications, and there is no need to project iteration results into space $R_{+}^n$ . Li et al. [15] [16] [17] [18] applied a class of modulus-based matrix splitting iteration methods to solving the nonlinear complementarity problem. Numerical results show that the methods are efficient. In the past decade many scholars have made many new achievements in this field, see the literatures [19] - [30] .

In this paper, we extend the modulus-based matrix splitting iteration methods to solve the large-scale stochastic linear complementarity problems. We also prove the convergence of these methods when the coefficient matrix is a positive definite matrix or a positive semi-definite matrix. The numerical results show that these methods are efficient.

The outline of the paper is as follows. In Section 2 we present some necessary results and lemmas. In Section 3 we establish the modulus-based matrix splitting iteration methods for solving the SLCP. The convergence of the methods is proved in Section 4. The numerical results are shown in Section 5. Finally, in Section 6, we give some concluding remarks.

2. Preliminaries

In this section, we briefly introduce some necessary results and lemmas.

Let $A=\left(a_{ij}\right)\in {ℝ}^{n\times n}$ , A is said to be positive semi-definite if $x^{\text{T}}Ax\ge 0$ for all $x\in {ℝ}^n$ , and positive definite if $x^{\text{T}}Ax>0$ for all $x\in {ℝ}^n\backslash \left\{0\right\}$ . $A\in R^{n\times n}$ is called a $P_0$ -matrix if all of its principle minors are nonnegative.

Let $\left(\Omega ,F,{\rm P}\right)$ be a probability space, where $\Omega$ is a sample subset of ${ℝ}^m$ . Suppose that probability distribution is known, we consider the stochastic linear complementarity problem (SLCP): finding a vector $z\in {ℝ}^n$ such that

$M\left(\omega \right)z+q\left(\omega \right)\ge 0,z\ge 0,z^{\text{T}}\left(M\left(\omega \right)z+q\left(\omega \right)\right)=0,\omega \in \Omega .$ (1)

where $M\left(\omega \right)\in {ℝ}^{n\times n}$ and $q\left(\omega \right)\in {ℝ}^n$ are the rand matrices and vectors for $\omega \in \Omega$ , respectively.

Usually there not exists z for all $\omega \in \Omega$ for Problem (1). In order to get a reasonable solution of (1), in this paper we use the EV formulation proposed by Gurkan et al. [1] .

The Expected Value (EV) Formulation [1] :

Let $F\left(z,\omega \right)=M\left(\omega \right)z+q\left(\omega \right)$ , $\bar{M}=\text{E}\left[M\left(\omega \right)\right]$ , $\text{q}=\text{E}\left[q\left(\omega \right)\right]$ , and E be the expectation. We consider the following EV formulation: finding a vector $z\in {ℝ}^n$ such that

$\bar{F}\left(z\right)=E\left[F\left(z,\omega \right)\right]=\bar{M}z+\text{q}\ge 0,z\ge 0,z^{\text{T}}\bar{F}\left(z\right)=0.$ (2)

We briefly denote it as $\text{LCP}\left(\text{q},\bar{M}\right)$ .

Define

$\text{RES}\left(z\right):=\min \left(z,\bar{M}z+\text{q}\right)$

where the min operator denotes the componentwise minimum of two vectors. It is generally known that $z^{*}$ solves the $\text{LCP}\left(\text{q},\bar{M}\right)$ if and only if $z^{*}$ solves the equations

$RES\left(z\right)=0$

The function RES is called the natural residual of the $\text{LCP}\left(\text{q},\bar{M}\right)$ and is often used in error analysis.

Lemma 1 (see [8] ) Let $\alpha \in \left(0,+\infty \right)$ be a scalar, then the $\text{LCP}\left(\text{q},\bar{M}\right)$ (2) is equivalent to the following fixed-point problem: finding $x\in {ℝ}^n$ , satisfying that

$\left(\alpha I+\bar{M}\right)x=\left(\alpha I-\bar{M}\right)\left|x\right|-\text{q}$ (3)

Moreover, if x is the solution of (3), then

$r:=\alpha \left(\left|x\right|-x\right)$ , $z:=\left|x\right|+x$ (4)

define a solution pair of Problem (2). On the other hand, if the vector pair z and r solves Problem (2), then $x:=1/2\left(z-r/\alpha \right)$ solves the fixed-point problem (3).

3. Modulus-Based Matrix Splitting Iteration Methods

In this section, we aim at the EV formulation of the stochastic linear complementarity problem (2). We give some corresponding modulus-based matrix splitting iteration methods.

For the strong monotone stochastic linear complementarity problem, the coefficient matrix is positive definite. For this case, we can apply the method proposed by Dong and Jiang [8] .

Method 3.1

Step 1: Select an arbitrary initial vector $x^{\left(0\right)}\in {ℝ}^n$ and set $k:=0$ ;

Step 2: Calculate $x^{\left(k\text{+}1\right)}$ through the iteration scheme

$\left(\alpha I+\bar{M}\right)x^{\left(k\text{+}1\right)}=\left(\alpha I-\bar{M}\right)\left|x^{\left(k\right)}\right|-q$

Step 3: Let $z^{\left(k\text{+}1\right)}=\left|x^{\left(k\text{+}1\right)}\right|+x^{\left(k\text{+}1\right)}$ , if $z^{\left(k\text{+}1\right)}$ satisfies the termination rule, then stop; otherwise, set $k:=k+1$ and return to Step 2.

Unfortunately, the coefficient matrices of some stochastic linear complementarity problems are positive semi-definite, Method 3.1 is not suitable for solving the problem (2). Cottle et al. [31] presented a regularization method. Based on this method, we establish a regularized modulus-based matrix splitting iteration method. To simplify the notation, we will denote $\left\{\epsilon \right\}$ and $\left\{x_{\epsilon }^k\right\}$ for $\left\{{\epsilon }_k\right\}$ and $\left\{x_{{\epsilon }_k}^k\right\}$ , and denote the regularization problem for $\text{LCP}\left(q,\bar{M}+\epsilon I\right)$ .

Method 3.2

Step 1: Select a positive number ${\epsilon }_0\in R$ and an arbitrary initial vector $x_{\epsilon }^{\left(0\right)}\in {ℝ}^n$ , and set $k:=0$ ;

Step 2: Generate the iteration sequence $x_{\epsilon }^{\left(k\text{+}1\right)}$ through solving the following equations

$\left(\alpha I+\bar{M}+\epsilon I\right)x_{\epsilon }^{\left(k\text{+}1\right)}=\left(\alpha I-\bar{M}-\epsilon I\right)\left|x_{\epsilon }^{\left(k\right)}\right|-q.$

Let $z_{\epsilon }^{\left(k\text{+}1\right)}=\left|x_{\epsilon }^{\left(k\text{+}1\right)}\right|+x_{\epsilon }^{\left(k\text{+}1\right)}$ .

Step 3: Set $\epsilon =\alpha \epsilon$ , where $\alpha \in \left(0,1\right)$ is a positive number, $k:=k+1$ , and return to Step 2.

4. Convergence

In this section, we analyze the convergence of Method 3.1 and Method 3.2 when the coefficient matrix of the $\text{LCP}\left(q,\bar{M}\right)$ is a symmetric positive definite matrix and a symmetric positive semi-definite matrix.

4.1. The Case of Symmetric Positive Definite Matrix

We first discuss the convergence of Method 3.1 when the coefficient matrix is symmetric positive definite.

Theorem 1 Suppose that the system matrix $\bar{M}\in {ℝ}^{n\times n}$ is symmetric positive definite, then the sequence $\left\{x^{\left(k\right)}\right\}$ generated by Method 3.1 converges to $x^{\ast }$ .

Proof. By Lemma 1 we get

$x^{\left(k+1\right)}={\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\left|x^{\left(k\right)}\right|-{\left(\alpha I+\bar{M}\right)}^{-1}q.$

If $x^{\ast }$ is a solution of (3), then

$x^{\ast }={\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\left|x^{\ast }\right|-{\left(\alpha I+\bar{M}\right)}^{-1}q.$

We can get that

$\begin{array}{c}\Vert x^{\left(k\text{+}1\right)}-x^{\ast }\Vert =\Vert {\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\left(\left|x^{\left(k\right)}\right|-\left|x^{\ast }\right|\right)\Vert \\ \le \Vert {\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\Vert \Vert \left|x^{\left(k\right)}\right|-\left|x^{\ast }\right|\Vert \\ \le \Vert {\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\Vert \Vert x^{\left(k\right)}-x^{\ast }\Vert \end{array}$

Since matrix $\bar{M}$ is a symmetric positive definite, we have

$\Vert {\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\Vert =\underset{{\lambda }_i\in \lambda \left(\bar{M}\right)}{\max }\left|\frac{\alpha -{\lambda }_i}{\alpha +{\lambda }_i}\right|:=\sigma \left(\alpha \right).$

where $\lambda \left(\bar{M}\right)$ denotes the set of all the eigenvalues of $\bar{M}$ . As ${\lambda }_i>0$ , it follows that

$\left|\frac{\alpha -{\lambda }_i}{\alpha +{\lambda }_i}\right|<1$

and thus

$\Vert {\left(\alpha I+\bar{M}\right)}^{-1}\left(\alpha I-\bar{M}\right)\Vert =\sigma \left(x\right)<1.$

Hence, by the Banach contraction mapping theorem, we have the convergence of the infinite sequence $\left\{x^{\left(k\right)}\right\}$ to the unique solution $x^{\ast }$ of the fixed-point equation.

4.2. The Case of Symmetric Positive Semi-Definite Matrix

We now discuss the convergence of Method 3.2 when the coefficient matrix is symmetric positive semi-definite.

Lemma 2 (See [31] ) Let $\bar{M}$ be a $P_0$ matrix, $\left\{\epsilon \right\}$ be a decreasing sequence, where $\epsilon$ is a positive scalar with $\epsilon \to 0$ . For each k, let $z^k$ be the unique solution of the $\text{LCP}\left(q,\bar{M}+\epsilon I\right)$ .

1) If $\bar{M}\in R_0$ , then the sequence is bounded; moreover, every accumulation point of 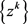solves the;

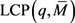2) If 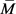is positive semi-definite and the 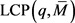is solvable, then the sequence converges to the least 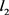-norm solution of.

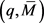Theorem 2 Suppose that the system matrix 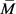is symmetric positive semi-definite, 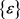is a decreasing sequence, then the infinite sequence 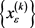produced by Method 3.2 is bounded. Moreover, every accumulation point of 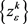solves the;

Proof Note that 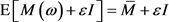is symmetric positive definite. By the Step (3) of Method 3.2, we can get

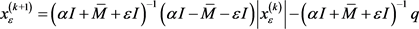
Then

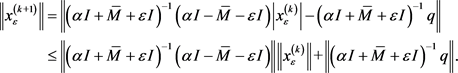
Let 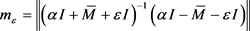and, there exist any positive numbers and, we have

, ,

Moreover,

Therefore

When, the infinite sequence is bounded. Since , we get that the sequence is bounded.

By Lemma 2, we have that every accumulation point of solves the LCP. The proof is completed.

5. Numerical Results

In this section, we test some numerical results to show the efficiency of our methods. Let, n be the order of the matrix, IT denote the average iteration steps, and CPU denote the average iteration time.

Let. The steps to generate test problems can be found in the literature [4] . Numerical experimental results are shown in Tables 1-3.

Table 1 shows that Method 3.1 is effective when the coefficient matrix is symmetric positive definite.

Table 2 and Table 3 list the numerical experimental results of Method 3.2 when the coefficient matrix is symmetric positive semi-definite. We know that Method 3.2 is effective. (In the following, we briefly denote that Feasible Semi-smooth Newton Method is FSNM.)

Table 4 shows that, Method 3.2 is more effective than FSNM [19] . By Tables 1-4, we know that Method 3.2 improves the computational efficiency and is suitable for solving the large scale problems.

Table 1. The numerical results of Methods 3.1 ().

Table 2. The numerical results of Methods 3.2 ().

Table 3. The numerical results of Methods 3.2 ().

Table 4. Comparison of numerical results of Method 3.2 and FSNM ^[19] .

6. Conclusion

In this paper, we study the fast numerical methods for solving the stochastic linear complementarity problems. Firstly, we convert the expected value formulation of stochastic linear complementarity problems into the equivalent fixed point equations, then we establish a class of modulus-based matrix splitting iteration methods, and analyze the convergence of the method. These new methods can be applied to solve the large-scale stochastic linear complementarity problems. The numerical results also show the effectiveness of the new methods.

Acknowledgements

This work was supported by Natural Science Foundation of China (11661027), National Project for Research and Development of Major Scientific Instruments (61627807), and Guangxi Natural Science Foundation (2015 GXNSFAA 139014).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gurkan, G., Ozge, A.Y. and Robinson, S.M. (1999) Sample-Path Solution of Stochastic Variational Inequalities. Mathematical Programming, 84, 313-333. https://doi.org/10.1007/s101070050024
[2]	Chen, X. and Fukushima, M. (2005) Expected Residual Minimization Method for Stochastic Linear Complementarity Problems. Mathematics of Operations Research, 30, 1022-1038. https://doi.org/10.1287/moor.1050.0160
[3]	Lin, G.H. and Fukushima, M. (2006) New Reformulations for Stochastic Nonlinear Complementarity Problems. Optimization Methods and Software, 21, 551-564. https://doi.org/10.1080/10556780600627610
[4]	Chen, X., Zhang, C. and Fukushima, M. (2009) Robust Solution of Monotone Stochastic Linear Complementarity Problems. Mathematical Programming, 117, 51-80. https://doi.org/10.1007/s10107-007-0163-z
[5]	Mangasarian, O.L. and Ren, J. (1994) New Improved Error Bounds for the Linear Complementarity Problem. Mathematical Programming, 66, 241-255. https://doi.org/10.1007/BF01581148
[6]	Zhou, G.L. and Caccetta, L. (2008) Feasible Semismooth Newton Method for a Class of Stochastic Linear Complementarity Problems. Journal of Optimization Theory and Application, 139, 379-392. https://doi.org/10.1007/s10957-008-9406-2
[7]	Zhang, C. and Chen, X. (2009) Smoothing Projected Gradient Method and Its Application to Stochastic Linear Complementarity Problems. SIAM Journal on Optimization, 20, 627-649. https://doi.org/10.1137/070702187
[8]	Dong, J.L. and Jiang, M.Q. (2008) A Modified Modulus Method for Symmetric Positive Definite Linear Complementarity Problems. Numerical Linear Algebra with Applications, 16, 129-143. https://doi.org/10.1002/nla.609 https://onlinelibrary.wiley.com/doi/10.1002/nla.609/
[9]	Bai, Z.Z. (2010) Modulus-Based Matrix Splitting Iteration Methods for Linear Complementarity Problems. Numerical Linear Algebra with Applications, 17, 917-933. https://doi.org/10.1002/nla.680
[10]	Bai, Z.-Z. and Evans, D.J. (2001) Matrix Multisplitting Methods with Applications to Linear Complementarity Problems: Parallel Synchronous and Chaotic Methods. Réseaux et Systèmes Répartis: Calculateurs Parallelès, 13, 125-154.
[11]	Bai, Z.-Z. and Evans, D.J. (2002) Matrix Multisplitting Methods with Applications to Linear Complementarity Problems: Parallel Asynchronous Methods. International Journal of Computer Mathematics, 79, 205-232. https://doi.org/10.1080/00207160211927
[12]	Bai, Z.Z. and Zhang, L.L. (2013) Modulus-Based Synchronous Multisplitting Iteration Methods for Linear Complementarity Problems. Numerical Algorithms, 62, 59-77. https://doi.org/10.1007/s11075-012-9566-x
[13]	Zhang, L.-L. (2012) On Modulus-Based Matrix Splitting Iteration Methods for Linear Complementarity Problems. Mathematica Numerica Sinica, 4, 373-386.
[14]	Zhang, L.T., Zhang, Y.X., Gu, T.X., Liu, X.-P. and Zhang, L.-W. (2017) New Convergence of Modulus-Based Synchronous Block Multi-Splitting Multi-Parameter Methods for Linear Complementarity Problems. Computational and Applied Mathematics, 36, 481-492. https://doi.org/10.1007/s40314-015-0238-z
[15]	Hong, J.T. and Li, C.L. (2016) Modulus-Based Matrix Splitting Iteration Methods for a Class of Implicit Complementarity Problems. Numerical Linear Algebra with Applications, 23, 629-641. https://doi.org/10.1002/nla.2044
[16]	Li, C.L. and Hong, J.T. (2017) Modulus-Based Synchronous Multisplitting Iteration Methods for an Implicit Complementarity Problems. EAST Asian Journal on Applied Mathematics, 7, 363-375. https://doi.org/10.4208/eajam.261215.220217a
[17]	Li, C.L. and Zeng, J.P. (2007) Multisplitting Iteration Schemes for Solving a Class of Nonlinear Complementarity Problems. Acta Mathematicae Applicatae, 23, 79-90. https://doi.org/10.1007/s10255-006-0351-2
[18]	Xia, Z.C. and Li, C.L. (2015) Modulus-Based Splitting Iteration Methods for a Class of Nonlinear Complementarity Problem. Applied Mathematics and Computation, 271, 34-42. https://doi.org/10.1016/j.amc.2015.08.108
[19]	Huang, Y.K. (2010) Research on Algorithms of Stochastic Linear Complementarity Problems. Xidian University, Xi’an.
[20]	Jiang, H. and Xu, H. (2008) Stochastic Approximation Approaches to the Stochastic Variational Inequality Problem. IEEE Transactions on Automatic Control, 53, 1462-1475. https://doi.org/10.1109/TAC.2008.925853
[21]	Ke, Y.F., Ma, C.F. and Zhang, H. (2018) The Modulus-Based Matrix Splitting Iteration Methods for Second-Order Cone Linear Complementarity Problems. Numerical Algorithms, 79, 1283-1303. https://doi.org/10.1007/s11075-018-0484-4
[22]	Ke, Y.F., Ma, C.F. and Zhang, H. (2018) The Relaxation Modulus-Based Matrix Splitting Iteration Methods for Circular Cone Nonlinear Complementarity Problems. Computational and Applied Mathematics, 37, 6795-6820. https://doi.org/10.1007/s40314-018-0687-2
[23]	Li, W. (2013) A General Modulus-Based Matrix Splitting Method for Linear Complementarity Problems of H-Matrices. Applied Mathematics Letters, 26, 1159-1164. https://doi.org/10.1016/j.aml.2013.06.015
[24]	Lin, G.H. (2009) Combined Monte Carlo Sampling and Penalty Method for Stochastic Nonlinear Complementarity Problems. Mathematics of Computation, 78, 1671-1686. https://doi.org/10.1090/S0025-5718-09-02206-6
[25]	Lin, G.H., Chen, X. and Fukushima, M. (2007) New Restricted NCP Function and Their Applications to Stochastic NCP and Stochastic MPEC. Optimization, 56, 641-753. https://doi.org/10.1080/02331930701617320
[26]	Lin, G.H. and Fukushima, M. (2009) Stochastic Equilibrium Problems and Stochastic Mathematical Programs with Equilibrium Constraints: A Survey. Technical Report 2009-008, Department of Applied Mathematics and Physics, Kyoto University, Kyoto.
[27]	Lin, G.H., Xu, H. and Fukushima, M. (2008) Monte Carlo and Quasi-Monte Carlo Sampling Methods for a Class of Stochastic Mathematical Programs with Equilibrium Constraints. Mathematical Methods of Operations Research, 67, 423-441. https://doi.org/10.1007/s00186-007-0201-x
[28]	Luo, M.J. and Lin, G.H. (2009) Convergence Results of the ERM Method for Nonlinear Stochastic Variational Inequality Problems. Journal of Optimization Theory and Application, 142, 569-581. https://doi.org/10.1007/s10957-009-9534-3
[29]	Zhang, C. and Chen, X. (2008) Stochastic Nonlinear Complementarity Problem and Applications to Traffic Equilibrium under Uncertainty. Journal of Optimization Theory and Application, 137, 277-295. https://doi.org/10.1007/s10957-008-9358-6
[30]	Liu, S., Zheng, H. and Li, W. (2016) A General Accelerated Modulus-Based Matrix Splitting Iteration Method for Solving Linear Complementarity Problems. Calcolo, 53, 189-199. https://doi.org/10.1007/s10092-015-0143-2
[31]	Cottle, R., Pang, J.S. and Stone, R. (1992) The Linear Complementarity Problem. Academic Press, San Diego, CA. http://link.springer.com/content/pdf/10.1007/978-94-015-8330-5_3.pdf