Effect of Doppler Shifts on Photon and Particle Flux of Beams

Samuel Lewis Reich

Tribco Inc., Cleveland, OH, USA.

DOI: 10.4236/jhepgc.2019.54055                

Abstract

Reasons are given for a Doppler shift on the number of observed (sensed) photons in a light beam not just a shift in frequency, also a similar (non-relativistic) effect on the number of observed (sensed) particles (with non-zero rest mass) in a particle beam. Optics texts have neither effect.

Keywords

Photon Flux, Beams, Intensity, Irradiance, Particle Flux

1. Observation of Objects on a Conveyor Belt [1]

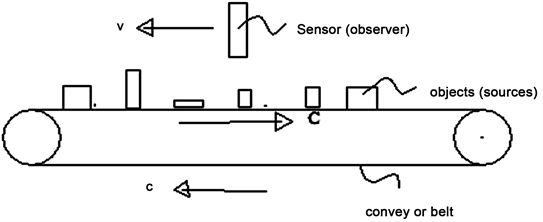
Every 1/ω seconds, an object placed on a conveyor belt moving with velocity c (a vector) I is energy flux (intensity of the light) seen by an observer, and I_o is I, at v = 0, where KA = any Doppler Shift of the cross-sectional area (velocity distortion of area) being observed moving in observer’s (sensor’s) reference frame, if the example in question has an area distortion. A ward-looking detector moving above the belt with a vector velocity v relative to the same stationary observer. The positive direction is a velocity moving from the source to the observer. Here, c is used because the belt speed has the same effect as the group velocity of light in the optical Doppler shift. θ is the angle between the two velocities. The closing velocity (the sum of the components of c and v moving the items toward the detector) is $\omega \left(c-v\cos \left(\theta \right)\right)$ .

As a result, in one second, $\left[\omega \left(c-v\cos \theta \right)/c\right]$ items are detected. That is the same equation as the axial Doppler shift of the frequency for waves moving at speed c and an observer with a velocity v at an angle θ to c. By changing c to speed of light one gets Doppler shift on particles of light photons.

Also it should be obvious from the definition of frequency as 1/(time period) that anything that changes observed frequency (like Doppler shifts) changes observed time periods including the period between photons. Since it has not been obvious for 100 years, [2] gives direct proof of that the axial Doppler changes observed time periods, based on the behavior of Fourier series of modulated signals. When the frequencies (of all harmonics of the series) are multiplied by the same factor K as in Doppler shifts (both axial and transverse). The value of any point in time of any of the harmonics occurs at t/K seconds in the shifted harmonic if it occurred at t seconds in the original harmonic term. Therefore, by superposition the value of every point at time t in the original modulated signal is not at time t/K. The observed time period time has been changed from t to t/K. The same would happen for the time period between observed photons.

2. For Beams Not Belts

The point being that the formula is universal and applies to all moving objects not just waves. In the case of particles in an electron beam or the photons in a light beam it applies to their flux (particles/(second × area)). This is besides the Doppler effect of frequency of the photon or energy of each particle. That means for light the Doppler effect on energy flux is:

$I/I_o={\left[1-\left(v/c\right)\right]}^2/KA$ (2-1)

I is energy flux (intensity of the light) seen by an observer, and I_o is I, at v = 0, where KA = any Doppler Shift of the cross-sectional area (velocity distortion of area) being observed moving in observer’s (sensor’s) reference frame, if the example in question has an area distortion.

Also it should be obvious from the definition of frequency as 1/(time period) that anything that changes observed frequency (like Doppler shifts) changes observed time periods including the period between photons. Since it has not been obvious for 100 years, [2] gives direct proof of that the axial Doppler changes observed time periods, based on the behavior of Fourier series of modulated signals when the frequency (of all harmonics of the series) are multiplied by the same factor as in Doppler shifts (both axial and transverse).

For a particle beam’s E:

$E/E_o=\left(m/m_o\right)\left[1-\left(v/c\right)\cos \theta \right]/KA$ (2-2)

Here unlike in light, c = the group velocity of the particles in the beam (which is belt velocity the last section) and (vcosθ) is the closing velocity between the observer (sensor) and the observed beam. E_o and m_o is E and m at v = 0. Note there is an observation angle θ, which becomes a dimension of everything that is distorted by velocity.

To simplify the above gave just only the axial shift for K, but transverse shift exists for light. Therefore the resultant K of the axial and transverse shift should be used in place of the axial shift alone when calculating things in the real world. There is no transverse shift for particle beams with a non-zero rest mass. To have a transverse shift the observed time of travel must be same for observation angles (an Einstein postulate). For light beams, people generally just multiply the axial and transverse shifts to get the resultant that is a few percent off, see [1] for a derivation of the resultant and other impacts of the axial Doppler shift.

3. Summary

Section 1 gave the thought experiment of objects on a conveyor belt being sensed by some electronic device such as a photo switch or a magnetic switch which is moving at other velocity and direction. The analysis showed the rate of observation of the objects is where v = the velocity the sensor is moving, c = the velocity the belt is moving, θ = the angel between the belt’s motion and a line of sight of the sensor, Ro = the rate the objects would be sensed if v = 0. That formula is exactly that of the axial Doppler shift. Instead of objects on a conveyor belt, it could be a stream of machinegun bullets or rain drops. [2] gives a mathematical proof that the axial Doppler shift like the transverse does change observed time periods (based on the behavior Fourier series of modulated signals).

The point being that formula is universal and applies to all moving objects, not just waves. In the case of particles in an electron beam or the photons in a light beam it applies to their flux (particles/(second × area)). This is besides the Doppler effect of frequency of the photon or energy of each particle. That means for light, the Doppler effect on energy flux is:

$I/I_o={\left[1-\left(v/c\right)\right]}^2/KA$ (3-1)

I is energy flux (intensity of the light) seen by an observer, and I_o is I, at v = 0.

But for a beam of particles (with a non-zero rest mass), c = group velocity of the particles (not speed of light). It is based on the motion of the sensor (observer) relative to the beam. The sensor in addition sees a smaller relativistic time change which must be added.

For a particle beam’s E:

$E/E_o=\left(m/m_o\right)\left[1-\left(v/c\right)\cos \theta \right]/KA$ (3-2)

where KA is the velocity distortion of the cross-sectional area of the beam if any, m is mass of a particle and m_o is ma at v = 0.

To simplify the above, only gave the axial shift, but transverse shift exists for light. Therefore, [K] and [KA] should be the resultant of the axial and transverse shift not just the axial shift alone for light. Reference [1] gives a slightly better resultant than multiplying the two shifts.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Reich, S.L. and Perera, W.G. (2019) The Difference in Mass between Relativity and Quantum Mechanics, Also Novel Effects of the Axial Doppler Shift. Journal of High Energy Physics, Gravitation and Cosmology, 5, 629-637. https://doi.org/10.4236/jhepgc.2019.53035
[2]	Reich, S.L. (2019) A Fourier Series Proof that All Optical Doppler Shifts Impacts Rate Information Is Transmitted and Its Probable Implication for Time. Reseachgate.net. https://doi.org/10.13140/RG.2.2.23539.89124