1. Introduction
1.1. Trade Description
In the Treasury lock transaction, termed T-Lock in the following, a Client willing to pre-hedge a prospected USD bond or loan issuance (Hedging Future Bond Issuance [1] , Valtchev [2] , LOCKING IN TREASURY RATES WITH TREASURY LOCK [3] ) will seek to enter a long T-Lock position with the Bank , with a given Expiry and written on a prescribed Security (most traditionally, a Treasury bond). Samples of T-Lock contracts within the ISDA Master Agreement framework can be found in [4] .
Being the driver of the fixed rate paid by the borrower the sum of its credit spread and the benchmark interest rate, the goal of such pre-hedge strategy is locking, when deemed economical, the interest rate component a few months ahead of the issue date. When considering a T-Lock as pre-hedge, the client is looking at the Treasury curve as the interest rates benchmark as opposed to looking at the swap rate curve. The choice of engaging in a T-Lock in lieu of a forward starting swap is mainly driven by the relative cost between the two strategies. An extensive illustration of the rationale for the use of T-Locks in comparison with other pre-hedging strategies can be found in Adam and Smith [5] .
Being long a T-Lock, at strike L (a.k.a. Locked Yield), means receiving at Expiry an amount equal to
(1)
where:
• N is the notional
• IRR is the internal rate of return of the prescribed security, prevailing at Expiry
• RiskFactor is minus the change of the bond’s price corresponding to a unitary shift of its internal rate of return1
The financing nature of the transaction, for which the hedge is intended, sees Expiry normally, at most, around 6 months (up to 12 months in very unusual cases) and L normally chosen to be close to the IRR seen at trade date, whilst deemed satisfactory enough by the Client to be locked at this level.
The Security can either be a specific existing Treasury (and the trade termed T-Lock as such or Standard T-Lock) or a Treasury to be identified at Expiry, i.e., the then On-The-Run n-Year benchmark (
, usually
and the trade termed Then-Current-T-Lock).
In both cases, if at Expiry the Treasury yield has increased, the Client will receive a dollar amount compensating the extra cost they will be incurring in borrowing money at a rate linked to the Treasury curve. Vice versa, Treasury yield tapering will generate a loss to the Client which, in turn, is financially compensated by a lesser cost in the borrowing transaction—in other words, via a long T-Lock position the Client is synthetically shorting the Security to the Bank until Expiry.
Hedge accounting-wise, the T-Lock can be designated as hedging item in a cash flow hedge relationship with an anticipated transaction, i.e., the borrowing transaction (the hedged item). As such, up until expiry the T-Lock P & L will be set aside in OCI. Then, if at expiry the borrowing materializes the P & L arisen from the T-Lock will be released amortized during the life of bond/loan (partially) offsetting, on a running basis, the cash flows generated during the debt servicing. On the other hand, if the financial close for the hedged item is not reached, the full P & L is recycled as a cost/income entry at expiry (Ramirez [6] [7] [8] , In depth: Achieving hedge accounting in practice under IFRS 9 [7] , Hedge accounting under IFRS 9 [9] ).
1.2. Pricing the Standard T-Lock
To begin with, recall that, if
is the price of the underlying Security as a function of the yield y, the internal rate of return IRR is by definition the yield such that
(2)
with
the (dirty) price of the bond.
The T-Lock prescribes the use of the compounded interest formula
(3)
where c is the coupon rate of the bond,
is the issue date,
the coupon payment dates (with
) and
the accrual factors. When t lies in a coupon period, i.e.,
, where
is the last coupon payment date, the formula generalizes to
(4)
which is basically (3) multiplied by the stub discount.
Defining the risk factor as
(5)
then the T-Lock payoff at
is equal to
(6)
where
for a long (unitary) position and
for a short (unitary) position and RiskFactor, IRR are evaluated at
.
From a different angle, at the first order,
(7)
(8)
(9)
so the T-Lock measures the gap between the market price of the bond and its price with flows discounted at rate L.
We will show that (9) actually identifies a overhedge/underhedge of the T-Lock, respectively for
and
.
In an arbitrage-free valuation framework, the general pricing formula (Hunt and Kennedy ( [8] , Corollary 7.34) reads
(10)
where the expected value conditional on the information available at t is computed with respect the
-forward measure and
is the risk-free zero coupon bond seen at t with maturity
. Due to the short term under consideration (
) and the quality of the issuer (the US government), default risk is ignored.
Working out the value from the formula above requires quite a modelling and computational effort but, because
can be interpreted as the (stubbed) swap rate (on a bond yield curve) fixing at
, if the uncertainty about
is ignored, the former summand can be seen as the payoff of a CMS-let based on the bond curve, i.e., in other words, that of a Constant Maturity Treasury swaplet (see Pucci [10] for a treatment of Constant Maturity Treasury swaps under relaxed assumptions where default of the bond issuer is also considered). Yet this interpretation is misleading because freezing
overshadows, and actually reverses, a key feature. Indeed, while a CMS-let has always positive convexity, the T-Lock has instead (at least locally near the Locked Yield) negative convexity as will be shown in Section 2.3 (page 16) Equation (43).
Given the complexity of addressing the modelling issues behind (10), let alone the availablity of a pricing function in the front office systems, a quick fix for the Bank to price and trade a short T-Lock position, in light of the typically short tenors clients need to cover, has been found in representing it as a plain forward contract. The following part of the paper analyzes the rationale of such operational practice.
1.3. Approximating a T-Lock as a Forward Contract
From (9), it can be seen that the payoff of a long Standard T-Lock struck at L may be approximated, at first order, by the t-value of a short forward contract struck at
. Moreover, because the convexity of the T-Lock is negative in non-extreme scenarios away for the current yield as shown in Section 2.3, such forward contract constitutes a overhedge for the trade, as can be also observed from the joint plot in Figure 1, with respect to security price, for a 3-month T-Lock written on the 10Y benchmark as of 24 January 2019, i.e. Treasury, coupon 3.125%, maturity 25 November 2028 (ISIN US9128285M81). The spot internal rate of return is 2.717% (
,
), the 3-months repo rate
, forward internal rate of return
(
,
) and
.
The identification of such overhedge suggests that a short position on the T-Lock may be proxied by a long position on the forward contract on the same underlying and struck at
(11)
(12)
where:
•
is the
-forward price at t for delivery of the Security at time
.
![]()
Figure 1. T-lock payoff and its overhedge.
•
is the risk factor of the Security as computed at time
•
is the
-forward internal rate of return of the Security as computed at time t, i.e., the rate such that
(13)
at
.
The forward contract proxy defined above may be regarded as a convenient representation of the Standard T-Lock in a practical situation where the T-Lock typology is not available in the trader’s front office risk management systems. In a later section we will analyse the risk generated by such approximation under standard mathematical assumptions that will make the treatment easier.
Because the security is not determined at inception, for the booking of the Then-Current-T-Lock a further issue arises. A natural extension is booking a Then-Current-T-Lock as a forward contract on the on-the-run benchmark as seen at inception and revise the booking each time a new on-the-run is taken over so that at
the proxy contract will match the real payout to the Client. Thus, for the purpose of investigating the pricing of a Then-Current-T-Lock, we turn our attention to the effect of replacing the security in the proxy forward contract.
Switching underlying security will lead to a new strike
(14)
with a strike gap, at first order,
(15)
(16)
We can see that, ignoring the jump in RiskFactor, a reasonable assumption if the switch is actually a benchmark replacement within the same tenor (e.g. 10Y) or within close-”in-the-run” bonds, the strike gap reads
(17)
The intuition is that the StrikeGap will generally be small if the switch is within close-”on-the-run” bonds but we will focus on this issue later in Section 3.1 turning our attention to a more meaningful measure, the P & L of the proxy forward contract.
From now on we will use Euler’s notation
for high-order differentials.
2. Hedging the Standard T-Lock
In the current section we will look at the greeks (Hull [11] , Chapter 19) generated by a standard T-Lock position, bearing in mind though that the same results apply to the Then-Current-T-Lock in-between roll events. The first two subsections are dedicated to the delta and gamma while in the third we touch on the practical implementation of the hedging strategy via the repo trade.
For ease of computation, we will assume the bond price to have the following functional form (Hull [11] , Section 4.8, page 91], Taleb [12] , page 184) with respect to the yield
(18)
where c is the coupon rate of the bond and
its accrual factors
Under this assumption, with R the internal rate of return,
(19)
(20)
(21)
Also, the first, second and third derivative of
are easily computed, respectively, as
(22)
which is a negative quantity (or null in limiting cases),
(23)
i.e., the so-called convexity of the bond (Taleb [12] , page 184)
(24)
which is positive, and finally,
(25)
which is negative.
As a consequence, the T-Lock payoff as a function of the yield
(26)
has first and second derivative, respectively,
(27)
(28)
and
(29)
2.1. The Overhedge Error
We’re now in the position of being able to evaluate the accuracy of approximation (9) which, looking at it backward, boils down to substituting P with its first order Taylor polynomial. The approximation is a (global) overhedge because the remainder
(30)
has a unique stationary point at
which is also a maximum, since the second derivative of
is negative.
Moreover, recalling the Remainder Estimation Theorem (see Apostol [13] ) which states that, for a differential function P and all y in an interval I containing a point a, the error in using the Taylor polynomial of degree n to approximate P satisfies
(31)
where M is the maximum value of
in the interval I, for
,
we have that
(32)
where, because the third derivative of P (that is, the first derivative of
), is negative,
is taken to be the value at the left-most point of the interval which is roughly (taking the extreme case
)
(33)
As an illustration, for the 10Y benchmark roughly
(34)
if we exclude the possibility of negative yields, an event that has never occurred (minimum yield for the 1Y Constant Maturity Treasury is 0.08% attained in September 2011). If we assume a 30% yield change, which is an upper bound for a short term such as 6 months for the 10Y benchmark, the dollar error amounts to 0.005% on 100% of notional.
2.2. Delta of the T-Lock
Thanks to the smoothness of
the greeks can be obtained by interchanging expected value and differentiation so for an analysis of delta and gamma of the T-Lock we will just look at the first and second derivatives of the payoff. From (28), when
, for
small enough (which is a reasonable assumption with short term expiries under typical business conditions),
(35)
so that the delta of the (long) T-Lock is negative
(36)
which is consistent with the previous comment about T-Lock being equivalent to shorting the security.
More precisely, resolving (28) for L, when
(37)
hence, because of the sign of the derivatives, we have a sharp lower bound smaller than y.
Turning things around
(38)
so, at least intuitively because the RHS of the inequality is also a function of y, as long as y does not overshoot L, the delta remains negative.
Taking into account the discounting, a trader, after booking the T-Lock position via proxy forward as argued in Section 1.3, may delta hedge a short position via shorting an amount of bond equal to
(39)
and continuously re-adjust the hedge as market and time move. So the question is how trading the delta will affect the bank’s P & L, so we turn our attention to the gamma.
2.3. Gamma of the T-Lock
In the following we investigate effectiveness of the replication via
-hedging of a T-Lock. From section (A) we have
(40)
(41)
From (28) and (29), the gamma of the T-Lock locally, i.e.,
small enough, satifies
(42)
(43)
So, when
, with
small enough, the Gamma is negative (i.e., the convexity of the T-Lock is negative), so dynamically replicating a T-Lock will, (not so) locally around L, generate rebalancing profits. In other words, dynamically replicating a long T-Lock via (10) and its delta assuming no volatility will be a overhedge, hence generating a non-negative P & L for the trader (see Carr and Madan [14] , Equation (9)). More precisely, using (41), we see that
(44)
The latter factor satisfies
(45)
Proof. Thanks to (87) (Appendix C), noting that the leading summands
and
cancel each other, we see that
(46)
(47)
This is because both summands are negative (from (88) and (89)) and the fact that
.
Finally, (44) and (45) yield
(48)
so, by the same argument shown above, as long as y does not overshoot L, the gamma remains negative as well. In Figure 2 we have plotted the T-Lock payoff along with its first derivative, i.e., its delta at expiry, with respect to security price. Also, notice in Figure 3 how both the delta and the gamma (here only reported at expiry for illustration) turn positive, as predicted by (37) and (48), in extreme high rate scenarios.
2.4. Replication of the T-Lock via Repo
We have already investigated the impact of delta hedging a short position in the T-Lock. The reader may have already noticed that what we have actually been looking at is the delta and gamma of the T-Lock with respect to the forward price of the bond, in other words the delta and gamma with respect to the forward contract as main security to be used in the replication strategy. This is actually appropriate since the shorting-the-bond requires to hedge the short position in the T-Lock can generally be accomplished only via a (reverse) repo trade and the delta (36), in terms of hedge ratio, is to be interpreted as the size of the corresponding repo to trade (for an extensive description of the workings of repo business see [15] ). Indeed, in Equation (13), but also in the exact approach (10), the repo rate comes into play because (see Section D).
(49)
where
is the (simply compounded) forward repo rate for the period
. We assume a zero haircut, which is a good approximation given the credit quality of the Treasury.
Due to (49), (13) and (22), since by the chain rule and assuming a flat short-term repo curve,
(50)
the sensitivity of the T-Lock to the repo rate is negative, so the higher the repo rate the cheaper is the long position.
The typical bid-ask spread for a repo transaction is 5 basis points. For instance, as of 24 Jan 2019, we report the repo curve in Table 1 for GC (General Collateral) which shows positive repo rates for all tenors but, since the security is normally chosen to be a benchmark Treasury, a specialness (negative) premium may apply so the repo rate may be significantly lower, increasing the fair value of the T-Lock position. Historically, in times of liquidity squeeze, the specialness has seen the repo rate on the 10Y Treasury momentarily drop into the negative axis at minus three hundred basis points (see Leong [16] ).
In passing, it’s also interesting to note that given the current regime in the EUR market, being repo rates in the negative space, a hypothetical T-Lock written on a European treasury bond would be more expensive relative to a traditional trade on a US Treasury.
3. Trading the Then-Current-T-Lock
As already represented in Section 1.3, in a Then-Current-T-Lock the underlying security is determined at
as the currently on-the-run benchmark. In the special and idealized case where
is coincides with the issue date of the new benchmark, the value at
of a long(short) Then-Current-T-Lock struck at L is proxied by a short (long) forward contract struck at
(51)
where
•
is that of the Proxy Security as computed at time
is the
-forward internal rate of return of the Proxy Security as computed at time t (see Equation (13))
![]()
Table 1. Repo rates for the 10Y as of 24 Jan 2019.
• Proxy Security is a traded security chosen in lieu of the yet unknown underlying, e.g., the on-the-run security as determined at time t.
At
the new security must be selected and a new strike populated, the strike gap being
(52)
In practice such a coincidence does not hold and because at inception the underlying security may be unknown and definitely not listed or identifiable in the position keeping system, the trader, via the procedure described in Section 1.3, may book the trade approximating the Then-Current-T-Lock as a Standard T-Lock with underlying security specified as the security that is on-the-run at trade inception. At each benchmark roll date
, the booking is revised with the on-the-run at
benchmark, generating a switch P & L, the roll P & L.
We will show in the approximated derivation (66) that the roll P & L must be small in special conditions. This is all the more the case at a on-the-run succession, i.e., when the security rolls from the previous on-the-run benchmark to the new on-the-run issue. Indeed, the new on-the-run will normally have an internal rate of return in line with the existing level and, if we also take into account that because of the high frequency of issue (e.g. trimestral for the 10Y) the on-the-run succession normally brings a new coupon that is very close to that of the previous on-the-run, the roll P & L is potentially even less significant.
3.1. The Roll P & L
In this section we will present an approximated formula for the Roll P & L that will allow us, in the conclusive part of the paper, to compute statistical estimates.
To keep things simple, assume the security is switched from a bond with coupon rate c to a bond with coupon rate
, all other details remaining equal. The net present value changes from
(53)
to
(54)
The P & L due to the switch is
(55)
with
,
and
(56)
so that
(57)
Now, by definition
(58)
and
(59)
therefore
(60)
(61)
(62)
where, when
is small, i.e., the bond at
is close to the bond’s maturity, the last summand
(63)
(64)
can be approximated, at first order, as
(65)
so that the (forward) P & L satisfies
(66)
(67)
(68)
(69)
(70)
(71)
Similarly, it can be shown that
(72)
(73)
Therefore, in as a much as
•
is small
• L is close to
• there is no significant gap in the internal rate of return between the two securities
The security change generates little P & L in the forward contract position.
More generally, in order to allow for longer tenor benchmarks, having defined
(74)
the removal of the restriction that
is small leaves us with
(75)
where
(76)
Having (75) at hand, we are now able to assess the impact of switching the underlying security of the contract at the issue of a new benchmark. To this aim, in the next section we will look at a stylized description of how a new benchmark is constructed, where we ignore the change in the tenor structure of the bond, only focusing on the determination of a new par coupon rate so that the new benchmark is priced at par.
3.2. Forming the New Benchmark
Treasury benchmarks are periodically reissued by means of an auction mechanism. The US government yearly publishes an auction calendar ( [17] ).
The roll process is described in the graph (Figure 4), where the bracketed exponent on
is a placeholder for the coupon rate, a process that runs as follows:
• First the internal rate of return
of the current benchmark is evaluated
• The prospected coupon
of the new benchmark is located so that the new issue is at par, i.e.,
• Then the auction will filter through market appetite determining a final coupon rate
• Finally, the new internal rate of return
is implied from
.
It’s clear that if the market confirms the new issue “at the old level” we land on
so, as can be elicited from Equation (75), minimizing the roll P & L.
Because the above assumptions are normally not verified, to estimate the roll risk in practice, in Section 4.3 we will resort to a statistical analysis based on the history of auctions.
4. Statistical Analysis
Looking at market data from January 2008 for the 2Y, 5Y and 10Y Treasury benchmark (see Figures 5-7), we have the following summary statistics in Table 2. The summary shows the average, the standard deviation and the two classic percentiles of the sample. Note that, in order to encompass non-standard scenarios, the data set includes the 2007 crisis.
![]()
Figure 5. Treasury 2Y: Internal rate of return and risk factor.
![]()
Figure 6. Treasury 5Y: Internal rate of return and risk factor.
![]()
Figure 7. Treasury 10Y: Internal rate of return and risk factor.
![]()
Table 2. Treasuries: Internal rate of return statistics.
In the following sections we will use such historical data to verify in practice our guess regarding the efficacy of managing the risk generated by short T-Lock positions by booking them as forward contracts. The statistical anaysis is aimed at estimating:
1) The overhedge error (Section 4.1) due to the payoff approximation illustrated in Section 1.3.
2) The gamma negativity bounds (Section 4.2), that is the stability of negative sign of the gamma across market scenarios.
3) The roll risk (Section 4.3) due to the P & L of the Bank generated during the life of the contract by the mispecification and consequent revision of the security underlying the sold T-Lock.
4.1. Overhedge Error Estimation
We first look at the overhedge error (9) by extracting a historical estimation for (32). Considering a 6M T-Lock on the 10Y benchmark, we find (Table 3) that
is on average 0.004% and at most (i.e. at 0.05% percentile) 0.0206%, and consequently (also recalling the estimate (34)), from (32) we have that the overhedge error is on average 0.32% of the notional and most likely bounded above by 1.55%, an event that materialized during the 2011 crisis that led to US
downgrade by the major rating agencies (Brandimarte and Bases [18] ). For the estimations in Table 3 we have assumed to be in a typical business case where the locked yield L to be set at the IRR seen at inception t, so that
is taken to be the 6-month performance
of the IRR. For ease of reading we omit reporting estimates for other cases, such as 3M, yielding similar results.
4.2. Negative Gamma Bounds
Considering the same historical window, in the following we have considered a daily time series of the upper bound (48) and reported in Tables 4-6 the relevant statistics. A move of such magnitude within the typical features (expiry and at-the-money strike) of a T-Lock trade is highly unlikely and has never been recorded being outside ordinary levels of core governative yields.
4.3. Assessment of the Roll Risk
We have considered roll data from January 2008 for the 10Y Treasury benchmark. It is a very large time window which is chosen to encompass extreme historical scenarios.
From Table 7, we see that, for the 10Y, the IRR change at roll dates tends to be higher than the IRR change on the whole sample. Consequently we expect P & L change an unfavourable on the T-Lock position at each benchmark switch.
To further the analysis, in the following we will look at the statistics regarding the actual P & L. Ignoring the discounting effect, which is a reasonable approximation by virtue of the short time horizon under scrutiny, we have considered a time series of (75) and computed the relevant percentiles and value-at-risk for the (forward) net present value of the forward contract for 1M, 3M, 6M, 12M expiries and 3% locked yield. From the point of view of the trader selling the T-Lock on the 10Y (Table 8): the average roll generates for the trader roughly a −0.105% of the notional loss which peaks at −1.04% at the 95-th percentile for the shortest expiry.
For the 5Y benchmark, data are more comfortable, showing a lower roll risk, both in the average and in the 95-percentile for all expiries (Table 9). For the 2Y benchmark, data are generally showing a lower roll risk, both in the average and in the 95-percentile for all expiries. We have also detected a robust insensitivity of the reported computation results to the choice of strike, so we here only focus on an indicative 3% level (Table 10).
![]()
Table 4. Upper bound for negative gamma for the 10Y.
![]()
Table 5. Upper bound for negative gamma for the 5Y.
![]()
Table 6. Upper bound for negative gamma for the 2Y.
![]()
Table 7. Treasury 10Y: Yield change.
5. Valuation Adjustments
Just as any derivative, a position on the T-Lock carries counterparty risk (see Gregory [19] , Morini and Prampolini [20] ). As such, CVA and DVA should also be included in the book value of the trade and in the final price to the client.
The calculation of such adjustments is a run-of-the-mill task for a bank dealing in derivatives but, whereas it may be argued that short-term trades generally attract low counterparty risk, we also notice that a T-Lock short position is subject to systemic wrong-way counterparty risk. Indeed, on a distressed scenario where the corporate market is undermined, a flight-to-quality ensuing regime may concurrently lower the Treasury spreads increasing the Bank exposure to the Client. It is difficult though to envision a situation where the corporate sector suffers and the banks thrive so it may be argued that the adverse move of the CVA may be offset by a specular increase in the DVA component, lowering the potential impact of wrong-way-risk on the bank’s balance sheet.
As for the FVA (Andresen, Duffie and Song [21] , Morini and Prampolini [20] , Albanese and Andreasen [22] ), having noticed that the natural hedge is a repo trade, a funding cost arises from the cash leg of the hedge the Bank is posting to borrow the security or from the collateralization mechanism if the repo is CSA-assisted or cleared.
From the point of view of the dealer bank, capital costs (KVA) are also minimal allowing for a interesting profitability of T-Locks although, by the same token, the trade will not afford high mark-ups.
Turning our attention to the proxy booking proposed, the overhedge nature the approximation will underestimate the exposure generated by the short T-Lock position, therefore underestimating the “contra” contribution (see Albanese and Andreasen [22] ) of counterparty risk, funding value adjustments and KVA. Nevertheless the short-term nature of the transaction under investigation will mitigate the consequences of such underestimation considering that XVA’s for at-the-money trades are normally priced at a fraction of the carried exposure.
6. Conclusions
We have shown that a long Standard T-Lock position has negative convexity, so the trader may safely (over-)replicate it by booking a linear trade, a proxy forward contract, which is a natural overhedge. In other words, a trader willing to sell a Standard T-Lock position can book the trade as a forward contract written on the same security and with the same expiry as that of the T-Lock contract. Being an overhedge, the forward contract will generate a conservative representation of bank’s P & L associated to the position. The negative convexity will ensure that delta hedging the positions will generate gamma profits. This comes in handy when the front office risk management system does not feature the T-Lock as a typology.
Moreover, we have shown that a T-Lock position is historically little sensitive to the benchmark roll. Therefore, a trader may book a Then-Current-T-Lock trade as a proxy forward contract written on the security that is on-the-run benchmark at inception and remain confident that revising the booking at roll dates to update the underlying will statistically generate a negligible P & L, while again, thanks to the negative convexity of the T-Lock, delta hedging the position in between roll dates will generate gamma profits.
Appendix
A. Simple Math
Below we recall simple facts about first and second derivatives of differentiable functions. If f and g are differentiable then
(77)
and
(78)
As a consequence, if f invertible and differentiable then
(79)
and
(80)
B. Key Derivatives
Noting that
(81)
and
(82)
(83)
we can work out that
(84)
(85)
and
(86)
(87)
C. More Math
Setting
,
we see that
(88)
because
is a clearly non-negative.
Moreover,
(89)
because
(90)
Indeed,
(91)
(92)
(93)
(94)
is clearly positive2.
D. The Forward Price and the Repo
A coupon security/dividend security X is a security that pays a discrete stream of cashflows
, each at time
. It could be either a stock or a coupon bond.
If
is the haircut, the T-forward price of the security, paying a dividend
at time
,
, is
(95)
(96)
where
is the repo rate,
is the funding rate for unsecured borrowing. Both rates are assumed continuously compounded and flat for ease of illustration.
Assuming first
, in a repo trade with dividends/coupons with maturity T the trader
1) Borrows in the time interval
an amount
of cash at rate
until T, with which s/he buys bond from the market and immediately transfers it to the repo counterparty.
2) Then for each 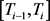 on each bond schedule node
on each bond schedule node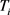 , receive coupon
, receive coupon ![]() and decrease the borrowed outstanding in the repo by
and decrease the borrowed outstanding in the repo by![]() .
.
3) At T, s/he gets the bond back, sells it in the market and returns all outstanding borrowed cash to the repo counterparty.
We describe our position by the quantity ![]() which represent the cash owned (plus sign)/owed (minus sign) to the repo counterparty, the repo account.
which represent the cash owned (plus sign)/owed (minus sign) to the repo counterparty, the repo account.
At start on the repo trade our repo account amounts to![]() . At each coupon payment we decrease the outstanding by the coupon amount. For instance, at
. At each coupon payment we decrease the outstanding by the coupon amount. For instance, at ![]() the repo account becomes
the repo account becomes
![]() (97)
(97)
Then, recursively, for![]() , at
, at ![]()
![]() (98)
(98)
and finally from ![]() to T it accrues to the terminal value
to T it accrues to the terminal value
![]() (99)
(99)
Working out the recursion we see the repo cash account grows as
Lemma 1. For all![]() ,
,
![]() (100)
(100)
So at maturity the strategy is worth
![]() (101)
(101)
In other words, the trader enters at t a contract at zero cost and ends up, via the repo strategy, at T with a ![]() in exchange for
in exchange for![]() , which means, by definition, that
, which means, by definition, that ![]() is the T-forward price of the security
is the T-forward price of the security
![]() (102)
(102)
If, on the other hand, due to market illiquidity the repo trade is not viable for the given security, the formula still holds but with ![]() in lieu of
in lieu of ![]()
![]() (103)
(103)
The two cases (102), (103) are the extreme cases:
• ![]() : all funding is secured since based on the repo trade
: all funding is secured since based on the repo trade
• ![]() : there is no repo trade, all funding is unsecured.
: there is no repo trade, all funding is unsecured.
Finally, for a generic haircut ![]() we obtain a “blend” formula:
we obtain a “blend” formula:
![]() (104)
(104)
![]() (105)
(105)
which may be derived from a strategy where coupon payments are distributed between repo redemption and unsecured funding redemption according to the their relative weights.
NOTES
*This paper expresses the views of its author and does not represent the opinion of Banca IMI SpA, which is not responsible for any use that may be made of its contents. Special thanks to Valeria Penn, Stefano De Nuccio, Luca Dominici, Luca Lovati, Luca Finicelli, Silvia Frasson and Emma Cardamone.
1In other words,
, where DV01 represents the price change corresponding to a basis point positive shift in the bond’s yield.
2For ease of reading, in the above summations we have omitted typing the conditions
and
.