Leibniz-Clarke Correspondence, Brain in a Vat, Five-Minute Hypothesis, McTaggart’s Paradox, etc. Are Clarified in Quantum Language ()
1. Review: Quantum Language (=QL = Measurement Theory)
Following refs. (Ishikawa, 2015b; Ishikawa, 2016a; Ishikawa, 2017d) , we shall review quantum language (i.e., the linguistic Copenhagen interpretation of quantum mechanics, or measurement theory), which has the following form:
(A)
(1)
We believe that quantum language is the only successful dualistic idealism in science.
In this paper we assume that “idealism” = “metaphysics” = “a discipline that cannot be verified by experiment”. Mathematics is of course successful metaphysics, but it is not dualistic.
1.1. Mathematical Preparations
Now we briefly introduce quantum language (=QL = measurement theory) as follows: (For details, see (Ishikawa, 2017d) ).
Consider an operator algebra
(i.e., an operator of all operators on a Hilbert space H) and consider the triplet
, called a basic structure.
Here,
is a C∗-algebra, and
is a particular C∗-algebra (called a W∗-algebra) such that
is the weak closure of
in
(Sakai, 1971; Prugovečki, 1982) .
Quantum language (=QL = the linguistic Copenhagen interpretation) is classified as follows (Ishikawa, 2006; Ishikawa, 2011; Ishikawa, 2017a) .
s (A1) quantum system theory (when
s (A2) classical system theory (when
That is, when =C(H), the C∗-algebra composed of all compact operators on a Hilbert space H, the (A1) is called quantum measurement theory (or, quantum system theory), which can be regarded as the linguistic aspect of quantum mechanics. Also, when
is commutative (that is, when
is characterized by C0(Ω), the C∗-algebra composed of all continuous complex-valued functions vanishing at infinity on a locally compact Hausdorff space Ω (Yosida, 1980) , the (A2) is called classical measurement theory.
Let
be a basic structure, and let
be the dual Banach space of A. That is,
= {ρ|ρ is a continuous linear functional on
}. Put
= {
|ρ is a pure state}.
Definition 1. [Observable] According to the noted idea (Davies, 1976) in quantum mechanics, an observable O := (X,
, F) in
is defined as follows:
1) [σ-field] X is a set,
(
2X, the power set of X) is a σ-field of X, that is, “
⇒
”, “
⇒
”.
2) [Countable additivity] F is a mapping from
to
satisfying: a): for every
, F(Ξ) is a non-negative element in
such that 0 ≤ F(Ξ) ≤ I; b):
and F(X) = I, where 0 and I is the 0-element and the identity in
respectively; c): for any countable decomposition
of Ξ (i.e., Ξ,
,
,
), it holds that
in the sense of weak∗ topology.
(For the more precise explanations, see (Ishikawa, 2017d) .)
1.2. Axiom 1 [Measurement] and Axiom 2 [Causality]
Measurement theory (A) is composed of two axioms (i.e., Axioms 1 and 2) as follows. With any system S, a basic structure
can be associated in which the measurement theory (A) of that system can be formulated. A state of the system S is represented by an element
and an observable is represented by an observable O := (X,
, F) in
. Also, the measurement of the observable O for the system S with the state ρ is denoted by M(O, S[ρ]) (or more precisely, M (O := (X,
, F), S[ρ])). An observer can obtain a measured value x (ÎX) by the measurement M (O, S[ρ]).
The Axiom 1 presented below is a kind of mathematical generalization of Born’s probabilistic interpretation of quantum mechanics. And thus, it is a statement without reality (i.e., a metaphysical statement).
Now we can present Axiom 1 in the W∗-algebraic formulation as follows. (For details, see (Ishikawa, 2017d) ).
Axiom 1 [Measurement]. The probability that a measured value x (ÎX) obtained by the measurement M (O := (X,
, F), S[ρ]) belongs to a set Ξ (
) is given by ρ(F(Ξ)).
Next, we explain Axiom 2. Let
and
be basic structures. Let
be a Markov operator (or, a causal operator).
Definition 2. [Sequential causal operator; Heisenberg picture of causality] Let (T, ≤) be a tree like semi-ordered set such that “t1 ≤ t3 and t2 ≤ t3” implies “t1 ≤ t2 or t2 ≤ t1”.
Define “
”
“
”. The family
is called a sequential causal operator, if it satisfies that
1) for each t (Î T), a basic structure
is determined.
2) for each
, a causal operator
is defined such as
, where
is the identity operator.
Now we can propose Axiom 2 (i.e., causality). (For details, see (Ishikawa, 2017d) ).
Axiom 2 [Causality]; For each t (ÎT = “tree like semi-ordered set”)), consider a basic structure:
, Then, the chain of causalities is represented by a sequential causal operator
1.3. The Linguistic Copenhagen Interpretation (=The Manual to Use Axioms 1 and 2)
Since so-called Copenhagen interpretation is not firm (Howard, 2004) , we propose the linguistic Copenhagen interpretation in what follows. In the above, Axioms 1 and 2 are kinds of spells, (i.e., incantation, magic words, metaphysical statements), and thus, it is nonsense to verify them experimentally. Therefore, what we should do is not “to understand” but “to use”. After learning Axioms 1 and 2 by rote, we have to improve how to use them through trial and error.
We can do well even if we do not know the linguistic Copenhagen interpretation (=the manual to use Axioms 1 and 2). However, it is better to know the linguistic Copenhagen interpretation, if we would like to make progress quantum language early.
Also, we believe that the linguistic Copenhagen interpretation is the true Copenhagen interpretation (Ishikawa, 2011; Ishikawa, 2017d) . Thus in this paper, the linguistic Copenhagen interpretation is sometimes called the Copenhagen interpretation.
In Figure 1 (mentioned later), we remark:
(B1) x : it suffices to understand that “interfere” is, for example, “apply light”.
y : perceive the reaction.
That is, “measurement” is characterized as the interaction between “observer” and “measuring object (=matter)”. However,
(B2) in measurement theory (=quantum language), “interaction” must not be emphasized. Therefore, in order to avoid confusion, it might better to omit the interaction “ x and y ” in Figure 1.
Also, since there is no measured value without observer (i.e., “I”, “mind”), we think that “measured value” belongs to “I” (=“observer”). Hence, we consider that measurement theory is composed of three key-words:
(B3):
(2)
such as in Figure 1 (Ishikawa, 2012a) .
For the further explanation of this figure, see (Ishikawa, 2017d) .
The linguistic Copenhagen interpretation says that
(C1) Only one measurement is permitted. Thus, Axiom 1 can be used only once.
And therefore, the state after a measurement is meaningless since it cannot be measured any longer. Thus, the collapse of the wavefunction is prohibited ((Ishikawa, 2015a) ; projection postulate). We are not concerned with anything after measurement. Strictly speaking, the phrase “after the measurement” should not be used. Also, the causality should be assumed only in the side of system,
however, a state never moves. Thus, the Heisenberg picture should be adopted, and thus, the Schrödinger picture should be prohibited.
(C2) “Observer” (=“I”) and “system” are completely separated. That is, any proposition (except Axiom 1) in quantum language is not related to “observer” (=“I”), therefore, there is no “observer’s space and time” in quantum language. And thus, it does not have tense (i.e., past, present, future).
(C3) there is no probability without measurements (Bertrand’s paradox in Section 9.12 of (Ishikawa, 2017d) , the probability in equilibrium statistical mechanics ( Ishikawa, 2012e ; Ishikawa, 2017d )).
(C4) Leibniz’s relationalism concerning space-time. See Section 4 later.
And so on.
We consider that the above (C1) is closely related to Parmenides’ saying (born around BC. 515 in ancient Greek) [There are no “plurality”, but only “one”] and Kolmogorov’s extension theorem (Kolmogorov, 1960) . For details, see (Ishikawa, 2017d) .
1.4. The History of World Descriptions
[The location of quantum language in the history of world-description (cf. (Ishikawa, 2012a; Ishikawa, 2017d) )]
In refs. (Ishikawa, 2015b; Ishikawa, 2017d) , we asserted that the ⑦, ⑧ and ⑨ imply that the following four are equivalent:
(D0) to propose quantum language (cf. ⑩ in Figure 2)
(D1) to clarify so-called Copenhagen interpretation of quantum mechanics (cf. ➆ in Figure 2) that is, the linguistic Copenhagen interpretation is the true Copenhagen interpretation. Also, as shown in Figure 3, the “→⑦” is called the linguistic Copernican revolution.
(D2) to find the final goal of the dualistic idealism (cf. ⑧ in Figure 2)
(D3) to reconstruct statistics in the dualistic idealism (cf. ⑨ in Figure 2, (Ishikawa, 2012c) )
![]()
Figure 3. Two kinds of Copernican revolutions.
1.5. The Copernican Revolution
In Figure 2, “→⑦” should be called “the linguistic CR (=Copernican Revolution)” in the following sense (cf. (Ishikawa, 2017b) ):
1) The recognitive CR: from “the world is previous, recognition is later” to “recognition is previous, the world is later”.
2) The linguistic CR: from “the world is previous, language is later” to “language is previous, the world is later”.
That is, we can illustrate as Figure 3.
Thus, Kant’s Copernican revolution (i.e., the above (1); (Kant, 1999) ) should be praised as the discovery of “idealism”, though the true scientific discovery of “idealism” may be due to the above linguistic CR.
1.6. Philosophy Made Progress
In the above Figure 2, let us focus on the history of the dualistic idealism in the linguistic world view such as
Plato → Descartes → Kant → Wittgenstein (3)
Note that physics obviously made progress in Figure 2, on the other hand, the (3)’s progress is not clear. However, we can introduce “progress” to the history of the western philosophy (or, the history of dualistic idealism) as follows. In (Ishikawa, 2016b; Ishikawa, 2017b) , we asserted that, if “(philosophical) progress” is defined by “approaching QL (=quantum language)”, then:
(E) the (3) does not only imply time series but also progress, that is,
(4)
Here
• Plato: the founder.
• Descartes: the discoverer of dualism (though the true scientific discovery is due to N. Bohr (Bohr, 1935) ). Also, Berkeley’s saying: “To be is to be perceived” is essential to idealism (cf. (Ishikawa, 2017c) ).
• Kant: the discoverer of idealism (in the sense of the above Section 1.5).
• Wittgenstein: he emphasized the importance of language.
This is natural since we assume [(D2); quantum language is the final goal of the dualistic idealism]. That is, we consider that the (4) is the history which gropes after the language in which science is written. Also, for the linguistic approach to the mind-body problem, see ref. (Ishikawa, 2017a) .
1.7. Quantum Language Is the Language to Describe Science
Also, since the (D) says that
“statistics”
“quantum information theory”
“dualistic idealism”
“quantum language”,
It is natural to assume that
(F) quantum language is the language in which science is written, that is, proposition in quantum language ⇔ scientific proposition (i.e., proposition which can be tested by experiment), which is the most important assertion of quantum language. This (F) is similar to the assertion: “Metaphysics dominates (physical) sciences”. Also, we assume that this (i.e., to make the language to describe sciences) is the true purpose of the philosophy of science. The usual problem “What is science?” is too ambiguous.
Remark 1. Note that the theory of relativity cannot be described by quantum language. However, we want to assert the (F). We think that the theory of relativity (and more, the theory of everything) is too special, an exception.
2. What We Cannot Speak about in Quantum Language
In this section we discuss the following well-known philosophical statements:
(G) “brain in a vat problem”, “the Cogito proposition”, “five-minute hypothesis”, “only the present exists”, “McTaggart’s paradox” and so on.
And we conclude that these are “what we cannot speak about in quantum language”, that is, non-scientific propositions (cf. the above (F)).
2.1. Brain in a Vat Argument
Suppose;
(H1) a mad scientist has removed your brain, and it into a vat of liquid to keep it alive and active. The scientist has also connected your brain to a powerful computer, which sends neurological signals to the brain in the way the brain normally receives them. Thus, the computer is able to send your brain data to fool you into believing that you are still walking around in your body. (See Figure 4, which is copied from “Brain in a vat” in Wikipedia https://upload.wikimedia.org/wikipedia/commons/4/4c/Braininvat.jpg).
Then, you may say;
(H2) “Am I a brain in a vat?” Or, “Can I answer to me whether I am a brain vat or not?”
Note that the question (H2) is related to “I”. Or, precisely, “observer” = “I”, “system (=measuring object)” = “I”, thus, “observer” and “system” are not separated. Thus, the linguistic Copenhagen interpretation (C2) says that this (H2) is not a statement in quantum language. Thus, the (H2) is not scientific, that is, there is no experiment to verify the statement (H2).
Although our argument (based on the linguistic Copenhagen interpretation) is quite simple, we believe that ours is superiority to Putman’s explanation using “metaphysical realism” (cf. (Putnam, 1982) ). That is because quantum language is the big theory that dominates sciences as mentioned in Section 1.7.
2.2. The Cogito Proposition
It is well known that R. Descartes proposed the Cogito proposition:
(I) “I think, therefore I am”, as the first principle of philosophy since he believed that this proposition (I) has no room for doubt. However, this is doubtful. Note that the proposition (I) is related to “I”. Or, precisely, “observer” = “I” and “system (=measuring object)” = “I”, thus, “observer” and “system” are not separated. Hence, the linguistic Copenhagen interpretation (C2) says that this (I) is not a statement in quantum language (Ishikawa, 2012b) . Thus, the (I) is not scientific, that is, there is no experiment to verify the statement (I).
2.3. What Is “I”?
Descartes proclaimed that he discovered “I”. Then, we have the natural question:
• What is “I” (discovered by Descartes)?
If (E) is true (i.e., Descartes
quantum language), this question can be answered as follows.
In quantum language, several words (“I” (=“observer”), “observable”, “matter”, “measurement”, etc.) are undefined such as point, line, plane etc. in Hilbert’s geometry (i.e., The Foundations of Geometry (1899)). D. Hilbert said that
• The elements, such as point, line, plane, and others, could be substituted by tables, chairs, glasses of beer and other such objects.
For example, the readers should note that the term “measurement” is used trickily in the quantum linguistic answer of Monty-Hall problem (Ishikawa, 2012d) .
2.4. Five-Minute Hypothesis
The five-minute hypothesis, proposed by B. Russell (cf. (Russel, 1921) ), is as follows.
(J1) The universe was created five minutes ago. Or equivalently, the universe was created ten years ago.
Now we show that this (J1) is not the statement in quantum language as follows (i.e., the first answer (1) and the second answer (2)).
The first answer (1): Note that this hypothesis (J1) is related to “tense”. Thus, the linguistic Copenhagen interpretation (C2) says that this (J1) is not a statement in quantum language. Thus, the (J1) is not scientific, that is, there is no experiment to verify the statement (J1).
The second answer (2): There may be another understanding as follows. If we consider that [“observer”
“the universe”], the proposition (J1) cannot be described in quantum language. That is because the linguistic Copenhagen interpretation (C2) says that “observer” (=“I”) and “measuring object” (=“the universe”) have to be completely separated.
Some may want to relate this hypothesis to skepticism (cf. (Russel, 1921) ), however we do not think that this direction is productive.
Remark 2. Also, the above (J1) should be compared to the following (J2)
(J2) The universe was created in A. D. 2008. (Or equivalently, now is A.D. 2018, and the universe was created ten years ago.)
This (J2) can be denied by experiment, that is, it is different from the fact. Thus, this is a proposition in quantum language.
2.5. Only the Present Exists
It is well known that St. Augustinus (AD.354-AD.430) said that
• the past does not exist because of its being already gone, that the future does not exist because of its not coming yet, and that the present really exists.
Here, consider:
(K) “Only the present exists”.
Note that this proposition (K) is related to “tense”. Thus, the linguistic Copenhagen interpretation (C2) says that this (K) is not a statement in quantum language. Thus, the (K) is not scientific, that is, there is no experiment to verify the (K).
2.6. McTaggart’s Paradox
In ref. (McTaggart, 1908) , McTaggart asserted “the Unreality of Time” as follows.
The sketch of McTaggart’s proof
(L1) Assume that there are two kinds of times. i.e., “observer’s time (A-series)” and “objective time (B-series)”. (Note that this assumption is against the linguistic Copenhagen interpretation (C2).)
(L2)・・・・・・
(L3) After all, the contradiction is obtained. Therefore, by the reduction to the absurd, we get;
(L4) A-series does not exist (in science).
About this proof, there are various opinions also among philosophers. Although I also cannot understand the above part (L2) (since the properties of A-series are unknown), I agree to him if his assertion is (L4) (cf. (Ishikawa, 2012a) ). That is, I agree that McTaggart noticed first that observer’s time is not scientific.
2.7. Is “What We Cannot Speak about We Must Pass over in Silence” True?
It should be noted that “what we cannot speak about” depends on language. As mentioned in the above, the followings are “what we cannot speak about in quantum language”:
• “brain in a vat problem”, “the Cogito proposition”, “five-minute hypothesis”, “only the present exists”, “McTaggart’s paradox” and so on.
However, thanks to Descartes said “I think, therefore I am”, dualism was developed. This fact may imply that
(M) “What we cannot speak about we must pass over in silence” is not true.
However, we think that Descartes’ success is accidental luck. Or, we may consider that the true discoverer of dualism is N. Bohr, the leader of the Copenhagen school. If Einstein believe in “What we cannot speak about (in Newtonian mechanics) we must pass over in silence”, he never discovered the theory of relativity. Since Wittgensteinin (Wittgenstein, 1921) said “The limits of my language mean the limits of my world.” he had should propose “my language”. We are sure that it will fall into a play on words by the argument without “my language”.
3. What Is Space-Time in Quantum Language?
The problems (“What is space?” and “What is time?”) are the most important in modern science as well as the traditional philosophies. In this section, reviewing ref. (Ishikawa, 2017d) , we give the quantum linguistic answer to these problems. As seen later, our answer is similar to Leibniz’s relationalism concerning space-time. In this sense, we consider that Leibniz is one of the discoverers of the linguistic Copenhagen interpretation.
3.1. How to Describe “Space” in Quantum Language
In what follows, let us explain “space” in quantum language. For example, consider the simplest case, that is,
(N) “space” =
(line (=one dimensional space))
Since classical system and quantum system must be considered, we see
(O1): a classical particle in the one-dimensional space
(O2): a quantum particle in the one-dimensional space
• In the classical case, we start from the following state:
(q, p) = (“position”, “momentum”) Î
Thus, we have the classical basic structure:
(P1) classical case
• Also, concerning quantum system, we have the quantum basic structure:
(P2) quantum case
Summing up, we have the basic structure
s (P1) classical case
s (P2) quantum case
Since we always start from a basic structure in quantum language, we consider that
• How to describe “space” in quantum language ⇔ How to describe [(O): space] by [(P): basic structure] (5)
This is done in the following steps.
Assertion 3. [The linguistic Copenhagen interpretation concerning space]
How to describe “space” in quantum language
(Q1) Begin with the basic structure:
,
(Q2) Next, consider a certain commutative C∗-algebra
(=C0(Ω)) such that
,
(Q3) Lastly, the spectrum Ω
is used to represent “space”.
For example,
s (R1) in the classical case (P1):
We have the commutative
such that
And thus, we get the space
(i.e., the spectrum) as mentioned in (O1)
s (R2) in the quantum case (P2):
We have the commutative
such that
And thus, we get the space
(i.e., the spectrum) as mentioned in (O2)
3.2. How to Describe “Time” in Quantum Language
In what follows, let us explain “time” in quantum language.
This is easily done in the following steps.
Assertion 4. [The linguistic Copenhagen interpretation concerning time]
How to describe “time” in quantum language
(S1) Let T be a linear tree like semi-ordered set. Usually it suffices to consider that
, or
(the set of all integer).
(S2) For each t (ÎT), consider the basic structure:
And consider a chain of causalities which is represented by a sequential causal operator
.
(S3) Then, the T can be used to represent “time”.
For the details, see ref. (Ishikawa, 2017d) .
4. Leibniz-Clarke Correspondence
The above argument urges us to recall Leibniz-Clarke Correspondence (1715-1716: (Alexander, 1956) ), which is important to know both Leibniz’s and Clarke’s (≈Newton’s) ideas concerning space and time.
• (T): [The realistic space-time]
Newton’s absolutism says that the space-time should be regarded as a receptacle of a “thing”. Therefore, even if “thing” does not exit, the space-time exists.
On the other hand,
• (U): [The metaphysical space-time] Leibniz’s relationalism says that
(U1) Space is a kind of state of “thing”.
(U2) Time is an order of occurring in succession which changes one after another.
Therefore, we consider the correspondence as
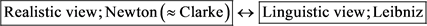
It should be noted that
• (V1) Newton proposed the scientific language called Newtonian mechanics, in which his absolutism (T) was explained. Therefore, it is understandable.
On the other hand,
• (V2) Leibniz could not propose a scientific language. Hence, Leibniz’s relationalism (U) is incomprehensible and literary.
However, I consider that Leibniz’s relationalism (U) can be formulated as mentioned in Section 3 in quantum language. Therefore, we assert that Leibniz’s relationalism (U) [=Assertions 3 and 4] should be regarded as one of the most important parts of the linguistic Copenhagen interpretation of quantum mechanics (see (C4) mentioned in Section 1.3).
Remark 3. Although N. Bohr himself might consider that he was on the side of the realistic view, in this paper we assume that he is on the side of the linguistic view. That is because we believe that the linguistic Copenhagen interpretation is the true Copenhagen interpretation. If so, we can say as follows.
As shown in Table 1, the great disputes in the history of the world view are always formed as follows:
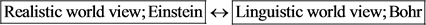
Cf. (Einstein et al., 1935; Bohr, 1935) .
For example,
![]()
Table 1. R (=the realistic world view) vs. L (=the linguistic world view).
(cf. Note10.7 in Chapter 10 (Section 10.7) of ref. (Ishikawa, 2017d) ).
5. Conclusion
Dr. Hawking said in his best seller book [A Brief History of Time: From the Big Bang to Black Holes, Bantam, Boston, 1990]:
• Philosophers reduced the scope of their inquiries so much that Wittgenstein the most famous philosopher this century, said “The sole remaining task for philosophy is the analysis of language.” What a comedown from the great tradition of philosophy from Aristotle to Kant!
We think that this is not only his opinion but also most scientists’ opinion. And moreover, we mostly agree with him. However, we believe that, if “the analysis of language” was rewritten to “the creation of language”, then Dr. Hawking would not have been critical to philosophy. That is because the task of physicists is just the creation of language, i.e., the language called Newtonian mechanics, the language called the theory of relativity, etc.
Also, since Wittgenstein said in (Wittgenstein, 1921) “The limits of my language mean the limits of my world”, he should have proposed “my language”. We are sure that the argument without “my language” will fall into a play on words.
Since the (F) says that “proposition in quantum language ⇔ scientific proposition”, it is worthwhile to see if the next propositions can be described in quantum language:
(W) “brain in a vat”, “the Cogito proposition”, “five-minute hypothesis”, “only the present exists”, “McTaggart’s paradox”, and so on.
And we showed that the above propositions in (W) are not propositions in quantum language, that is, these are not scientific.
Also, in Section 4, we emphasize that Leibniz’s relationalism in Leibniz-Clarke correspondence is clarified in quantum language, and it should be regarded as one of the most important parts of the linguistic Copenhagen interpretation of quantum mechanics.
I hope that these will be examined from various points of view1.
NOTES
1For the further information of quantum language, see my home page: http://www.math.keio.ac.jp/~ishikawa/indexe.html.