A Hidden Stability in the Random Behaviour of the Consecutive Prime Numbers ()
1. Introduction
In 1886, the German mathematician Leopold Kronecker attended the reunion of natural scientists in Berlin and said: “God made the integers; all else is the work of man.” The famous quote, echoing Pythagoras’ opinion, was cited by H. Weber in an obituary published in 1891 and more recently mentioned on the page 480 of the book [ 1 ] and on the page 13 of the book [ 2 ]. If we go a little deeper into the structure of natural numbers, it would be probably more adequate to say that “God created the prime numbers; all else is the work of man”, because every integer is either a prime number or a unique product of primes. However, the generation of the prime numbers, the building bricks of number theory, is quite mysterious, defying any regularity, and being rather random. As mentioned on page 163 of the book [ 3 ], “Prime numbers have always fascinated mathematicians. They appear among the integers seemingly at random, and yet not quite. There seems to be some order or pattern, just a little below the surface, just a little out of reach.”
There are many studies about the primes. As mentioned in [ 4 ], some results refer to the behavior of the large primes. Thus, for instance, it has been proved that, asymptotically, the number of primes not exceeding the positive real number x behaves, roughly speaking, like
. The asymptotic results, however, do not give good approximations when they are applied to the prime numbers from the range accessible to us. Consequently, examining empirically the first known primes, and assisted by more and more powerful computers that could generate prime numbers up to 1018, many conjectures about the behavior of primes have been formulated. In particular, conjectures on the gap between primes have been a frequent topic in number theory. The gap between consecutive prime numbers,
, where
is the n-th prime number, generally increases with n but even though primes get increasingly rare as we go further out along the number line, we will not stop finding pairs of primes that are very close. The twin primes conjecture states that there are infinitely many pairs of primes that differ by only 2. Thus, (3, 5), (5, 7), or (71, 73) are obvious twin primes, but, according to [ 5 ], the pair of big numbers (18,409,199, 18,409,201) are also twin primes. According to Webster’s New Collegiate Dictionary, a conjecture is a conclusion deduced by guesswork from evidence. A conjecture could be true but has not been proved yet. As more and more primes satisfy a certain conjecture about them, its credibility increases but as large the number 1018 is, it is still a finite number, whereas the set of prime numbers is infinite. The conjectures involving primes are useful and some are very ingenious but what is really needed is to get some statements and properties satisfied by all prime numbers, or at least to detect some kind of stability in the obvious random behavior of the primes.
2. GEOMETRIC INTERPRETATION OF ANDRICA’S CONJECTURE
There is an inequality constraint that is satisfied by every pair of consecutive prime numbers. Using only words, it says that for every pair of consecutive primes, the difference between their arithmetic mean and their geometric mean divided by the gap between the two primes is smaller than 0.5. We do not know how the primes are generated and how the gap between consecutive primes behaves but if we divide the difference between the arithmetic mean of two consecutive primes and their geometric mean by the gap between these primes we always obtain a number belonging to the interval (0, 0.5). At least something is stable in the random world of prime numbers. Using mathematical notations, if
and
are consecutive primes, then:
. (1)
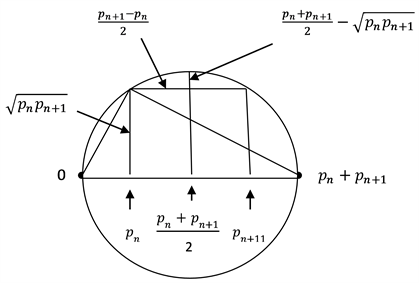
It is not very common to use geometry in number theory. In this case, however, it is enough to take a
circle of diameter
centered at
and it is possible to visualize all the components of
inequality (1), as indicated in the following figure. In particular, it offers a proof without words of the well known fact that the geometric mean cannot exceed the arithmetic mean, namely,
.
The geometric representation is very clear but it does not prove inequality (1). In order to do so, let us assume that
, where k is a natural number. We have:
. (2)
Indeed, if this is not true, then:
,
which implies:
.
Thus, assuming that (2) is not true, we arrived to:
,
which is absurd. Therefore (2) is true and, taking into account that:
,
it is equivalent to (1).
Let us notice that the only consecutive primes for which the gap between them is not an even number are:
and
. But for them:
and (1) is satisfied as well.
Let us notice that inequality (1) is true if
and
are replaced by arbitrary primes p and q, such that
. In fact, it continues to be true for any pair of positive real numbers x and y such that
but, obviously, there are infinitely many pairs of positive real numbers x, y, such that
, for which the ratio
does not belong to the interval (0, 0.5).
As the gap between consecutive primes could be large, inequality (1) does not tell us how small the difference between the arithmetic mean and the geometric mean of the consecutive primes should be. Before discussing this issue, let us notice that the square root of the difference between the arithmetic men and the geometric mean of the consecutive prime numbers is equal, up to a multiplicative positive constant, to the gap between the square roots of the respective consecutive primes, namely:
(3)
Taking (3) into account, inequality (1) is equivalent to:
. (4)
In particular, for twin primes we have
, and inequality (4) becomes:
.
As the gap between consecutive primes could be large, inequality (4) does not tell us how small the gap between the square roots of the consecutive primes should be. In 1986, Andrica ([ 6 ]) formulated the conjecture claiming that:
. (5)
As of 2008, the inequality (5) has been mentioned to hold true for n up to
, but it is still a conjecture, based on the empirical observations of the tables with prime numbers. It gives an empirical upper bound for the gap between the square roots of the consecutive prime numbers but tells us noting about how these gaps behave. Inequality (5) is still a conjecture but the inequality (4) shows, with certainty, that in spite of the apparently random way in which the prime numbers appear in the sequence of positive integers, they still obey the regularity expressed by inequality (4).
3. FLUCTUATIONS OF THE GAP BET WEEN THE SQUARE ROOTS OF THE CONSECUTIVE PRIMES AROUND THE MEAN GAP
We can see, however, that even if the gaps between consecutive prime numbers have random lengths, the actual gaps between the square roots of the consecutive primes fluctuate but remain very close to the values of the corresponding expected gaps. Dealing with the gaps between the square roots of the consecutive prime numbers, we can see a striking statistical stability, which cannot be detected when we look at the gaps between the corresponding consecutive prime numbers.
In order to make everything more intuitive, let us consider that customers arrive randomly, one by one, in a shop and look at
as being the time at which the n-th customer arrives. With respect to
consecutive random arrivals, the actual interarrival time between the n-th and the
-th customers is:
, (6)
whereas the expected (or average, or mean) interarrival time is:
. (7)
We want to illustrate the fact that the actual gaps (6) fluctuate but remain very close to the corresponding expected gaps (7), showing a surprising statistical stability. We take four very different segments of consecutive prime numbers and we analyze this conjecture about the behavior of the actual gaps (6). In this task, very useful tools proved to be Wolfram’s computer subroutines ([ 5 ]): Prime [n], giving the n-th prime number, and PrimePi [x], giving the number of primes not exceeding the real number x, known in number theory as the function
.
Example 1: The first 27 consecutive prime numbers (n = 1, ..., 27). They are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103. The gaps between them are quite chaotic, namely, 1, 2, 2, 4, 2, 4, 2, 4, 6, 2, 6, 4, 2, 4, 6, 6, 2, 6, 4, 2, 6, 4, 6, 8, 4, 2, fluctuating heavily between 1 and 8. Figure 1 shows the actual gaps (6) between the square roots of these primes, represented by the dots on the solid line segments, and the expected gaps (7), represented by the corresponding dots on the dashed line segments. The actual gaps fluctuate as well, but only between 0.118 and 0.671, and remarkably remain very close to the corresponding expected gaps, which are more stable, changing only between 0.318 and 0.451. The differences between the expected gaps (7) and the corresponding actual gaps (6) belong to the short interval [−0.195, 0.248].
Example 2: From the 500th to the 520th consecutive prime numbers (n = 500, ..., 520). They are: 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727. The gaps between them are even more chaotic, namely, 10, 2, 10, 14, 6, 4, 6, 8, 6, 6, 16, 12, 2, 4, 14, 6, 4, 8, 10, 8, 6, fluctuating between 2 and 16. Figure 2 shows the actual gaps (6) between the square roots of these primes, represented by the dots on the solid line segments, and the expected gaps (7),
![]()
Figure 1. The dots on the solid line segments and the dots on the dashed line segments show the values of the actual gaps and of the expected gaps, respectively, between the square roots of the consecutive prime numbers from 2 to 103.
![]()
Figure 2. The dots on the solid line segments and the dots on the dashed line segments show the values of the actual gaps and of the expected gaps, respectively, between the square roots of the consecutive prime numbers from 3571 to 3727.
represented by the corresponding dots on the dashed line segments. The actual gaps fluctuate as well, but only between 0.017 and 0.132, and remain very close to the corresponding expected gaps, which are more stable, changing only between 0.115 and 0.117. The differences between the expected gaps (7) and the corresponding actual gaps (6) belong to the short interval [−0.016, 0.100].
Example 3: From the 30797th to the 30807th consecutive prime numbers (n = 30,797, ..., 30,807). They are: 360,589, 360,593, 360,611, 360,637, 360,649, 360,653, 360,749, 360,769, 360,779, 360,781, 360,803. The gaps between them are even more chaotic, namely, 4, 18, 26, 12, 4, 96, 20, 10, 2, 22, fluctuating widely between 2 and 96. Figure 3 shows the actual gaps (6) between the square roots of these primes, represented
![]()
Figure 3. The dots on the solid line segments and the dots on the dashed line segments show the values of the actual gaps and of the expected gaps, respectively, between the square roots of the consecutive prime numbers from 360,589 to 360,803.
by the dots on the solid line segments, and the expected gaps (7), represented by the corresponding dots on the dashed line segments. The actual gaps fluctuate as well, but only between 0.003 and 0.080, and remain very close to the corresponding expected gaps, which are stable, at the value 0.019. The differences between the expected gaps (7) and the corresponding actual gaps (6) belong to the very short interval [−0.061, 0.017]. The gaps between the consecutive prime numbers increase whereas the gaps between the square roots of the consecutive prime numbers become smoother, remaining closer to the corresponding expected gaps between them.
Example 4: From the 486570082th to the 486570092th consecutive prime numbers (n = 486,570,082, ..., 486,570,092). They are: 10,726,904,533, 10,726,904,577, 10,726,904,599, 10,726,904,603, 10,726,904,633, 10,726,904,659, 10,726,905,041, 10,726,905,097, 10,726,905,103, 10,726,905,121, 10,726,905,139. The gaps between them are strikingly chaotic, namely, 64, 2, 4, 30, 26, 382, 56, 6, 18, 18, fluctuating widely between 2 and 382. Figure 4 shows the actual gaps (6) between the square roots of these primes, represented by the dots on the solid line segments, and the expected gaps (7), represented by the corresponding dots on the dashed line segments. The actual gaps fluctuate as well, but only between 0.00000 and 0.00184, and remain very close to the corresponding expected gaps, which are stable, at the value 0.00021. The differences between the expected gaps (7) and the corresponding actual gaps (6) belong to the very short interval [−0.00163, 0.00021]. Again, the gaps between the consecutive prime numbers increase whereas the gaps between the square roots of the consecutive prime numbers become smoother, remaining very close to the corresponding expected gaps between them.
The fluctuation of the gap between the square roots of the consecutive prime numbers:
(8)
around the mean gap:
(9)
is their difference:
. (10)
![]()
Figure 4. The dots on the solid line segments and the dots on the dashed line segments show the values of the actual gaps and of the expected gaps, respectively, between the square roots of the consecutive prime numbers from 10,726,904,659 to 107,269,050.
The excess of the fluctuation (10) is:
.
The recess of the fluctuation (10) is:
.
To give a numerical example, for the consecutive prime numbers
and
, the gap (8) between their squares is:
and the mean gap (9) at this stage is:
.
The corresponding fluctuation (10) is:
.
The excess is
and the recess is
.
The empirical evidence given in this section seems to justify the behavioural conjecture that the fluctuations of the gap (8) are closer and closer to the mean gap (9) when n increases.
4. A CONJECTURE EQUIVALENT TO ANDRICA’S CONJECTURE
Summarizing, let
be the prime numbers. Intuitively, assume that in a
system, the n-th customer arrives at time instant
. The interarrival time is
. There are n
customers arriving during the time interval
. The mean interarrival time is:
.
The interarrival time fluctuates around the mean interarrival time. The excess is defined by:
if the interarrival time is larger than or equal to the mean interarrival time. A simple algebra shows that the following conjecture:
(11)
is equivalent to Andrica’s conjecture:
, (12)
but the conjecture (11) is more intuitive than (12), giving an upper bound for how much the interarrival time could exceed the mean interarrival time.
Let also notice that Andrica’s conjecture (5), which states that the interarrival times:
belong to the unit interval [0, 1], implies that the mean, or average, interarrival times also belong to the unit interval, i.e.
or, that:
.
5. CONCLUSION
The gap between consecutive prime numbers fluctuates randomly. The paper brings empirical evidence showing that the fluctuations of the gap between the square roots of the consecutive primes seem to stabilize more and more around the mean gap when larger consecutive primes are taken into account. Andrica’s conjecture is equivalent to imposing a bound for the upper deviation from the mean gap.