Frobenius Series Solutions of the Schrodinger Equation with Various Types of Symmetric Hyperbolic Potentials in One Dimension ()

1. Introduction
The exact solution of the Schrödinger equation (SE) can be obtained only for a few particular forms of potentials. In other cases, one has to appeal to approximations or numerical techniques.
Many approximation methods have been developed for solving problems in one-dimensional space, among which the power series method and its extension were known as the Fröbenius method (FM) [1] .
The power series method is the standard method for solving linear ordinary differential equations with variable coefficients. It gives solutions in the form of a power series expansion about any desired point
. The FM generalizes the power series one. It gives solutions in the form of a power series expansion, multiplied by a logarithm term
or a fractional power
[2] .
In this paper, we show that highly accurate solutions to the SE can be determined for various types of symmetric hyperbolic potentials by the use of the FM. The potentials we consider here belong to a class of hyperbolic potentials given by
(1)
where
,
and coefficients
,
are not simultaneously zero. This potential can be reduced to the hyperbolic Pöschel-Teller potential (HPTP) [3] [4] [5] which occurs in the study of solitons [6] [7] and the Manning potential (MP) [8] which can be used to study polyatomic molecular vibrations [8] [9] . We can verify that it also contains the family of potentials
defined by
(2)
where
and
. Furthermore, the class of potentials
under consideration has another interesting aspect that it can be used to model the Gaussian function of the form
(3)
by suitably choosing the values of
and
,
.
Based on the foregoing, it can be said that the class of potentials (1) is composed of many types of hyperbolic potentials and several approximations of the Gaussian function. It therefore has the ability to explain various physical phenomena. Consequently, it is of considerable interest to find general solutions of its associated SE. In this work, we aim to present Fröbenius series solutions of this equation and discuss several members of the family of potentials under consideration.
The rest of this paper is organized as follows. In section 2, we convert the SE into a dimensionless eigenvalue problem which can be solved by means of the FM, and give recurrence relations for the expanding coefficients of the generalized power series for the wave functions. We also show how to determine bound state energies and wave functions. Furthermore, we derive the normalization constants for odd and even bound state eigenfunctions. In section 3, we present and comment results for two special cases, i.e., the case of the HPTP and that of the MP. In section 4, we apply the FM to a potential of type (1) modeling the function
, with an application to the Gaussian potential well (GPW). The conclusion is given in Section 5.
2. Derivation of Even and Odd Series Solutions
2.1. Dimensionless Schrödinger Equation
The time-independent Schrödinger equation for a particle of mass m that moves in one dimension
under the effect of the potential (1) is
(4)
or
(5)
where
. (6)
Rewriting Equation (5) with a new variable of the form
, such that the domain
maps to
and
(7)
we obtain
(8)
2.2. Expansion around a Regular-Singular Point
It is clear that
and
are both regular-singular points for the differential Equation (8). The FM can therefore be applied with the wave function represented as
,
(9)
or
,
. (10)
Let us seek
in the form (10). We first make the substitution
. The resulting differential equation, i.e.
(11)
can be solved near
by writing
(12)
It is worth noting that the
coefficients that appear in Equation (11) are calculated from the two following expressions:
(13)
,
(14)
where
denotes the number of combinations of j objects taken i at a time.
Putting Equation (12) and its two first derivatives into Equation (11) we get, after some reduction:
(15)
The smallest power is
. It appears in the first series. By equating its coefficient to zero, we obtain the indicial equation
(16)
whose solutions are
and
. We can therefore conclude that the two solutions of the SE obtained as generalized series, one with
and the other with
, are linearly independent. The value of
determines the behavior of
for
and
. Clearly, only
is acceptable for odd states since in this case
. On the other hand,
is suitable for even states.
To sum up:
・ Odd solutions contain only the series with
, and in the following will be denoted by
(17)
where the dependence on the eigenvalue is explicitly marked. The coefficients
are given by the
-term recurrence relation
(18)
with the understanding that
.
・ An even solution can be written as a power series
(19)
where the coefficients
are given by the
-term recurrence relation
(20)
2.3. Bound State Energies and Wave Functions
The function
has an important property that
, which can be regarded as a boundary condition for odd wave functions. For even wave functions, we choose
as boundary condition at this point. These conditions are sufficient to ensure that
and
are linearly independent.
If
(resp.
) is associated with a bound state, it has another important property, i.e.
(resp.
), which can be considered as the boundary condition for bound state wave functions at
. It means that for arbitrary
, the wave functions
and
obtained from Equations (17) and (19) are not square integrable. In other words, this condition determines the energies of the discrete spectrum. Substituting the calculated bound state energy to the recursion relation (18) or (20), the coefficients of the generalized series (17) or the power series (19) can be successively determined in order to obtain the wave function as a sum of the series.
We have to emphasize that in practice, the function
(resp.
) has to be approximated by truncating the series in Equation (17) (resp. (19)) at suitably high order N. The truncated function is a polynomial of degree N in the variable
whose zeros correspond to bound state values of
. If for two neighboring values of
the wave function takes values of different signs, we can deduce that one bound state reduced energy (
) lies between these two values. The bound state reduced energy in question can be computed numerically by means of the dichotomy method [10] with an arbitrary chosen precision.
2.4. Bound State Wave Function Normalization Constants
In order to facilitate the calculation of odd and even wave function normalization constants, we consider only the first
terms in the generalized series (17) and the power series (19), N being sufficiently large. More precisely, we write the wave functions
and
in the forms
(21)
and
(22)
wherewe have used the fact that
and
. Note that the parity of the wave functions
areexplicitly marked in the
coefficients, and that
and
design the normalization constants for odd and even states respectively. These constants are obtained from the equations
(23)
and
. (24)
In view of the boundary condition for bound state wave functions at
, we have the following approximate equations:
,
. (25)
Using these approximations, we can rewrite Equations (21) and (22) as
(26)
and
(27)
By inserting Equation (26) (resp. (27)) in the left hand side of Equation (23) (resp. (24)) and then using the remarkable identities
(28)
and
(29)
we obtain:
(30)
(31)
with
(32)
(33)
Changing variables from x to
and using the fact that
, (34)
we find
, (35)
(36)
where
.
It follows immediately from Equations (35) and (36) that
(37)
and
. (38)
3. Numerical Results for Two Special Cases
3.1. Hyperbolic Pöschl-Teller Potential
In order to test the reliability and efficiency of the FM for the class of potentials (1), we here consider the HPTP
,
(39)
which corresponds to the special case where
and
. This potential is exactly solvable. The bound state energies are given by [3] [11] :
(40)
with
. The associated wave functions can be written as
(41)
where
. (42)
The normalization constants
are obtained from the equation
and can be expressed as follows:
(43)
with
(44)
where
is the Pochhammer symbol, i.e.,
,
. (45)
Table 1 displays bound state energies for
,
and
in atomic units (
and
), where
designs the electron mass. The exact energies (
) are reported in the second column; those calculated by means of the FM are given in the third, fourth and fifth columns for three values of N (
,
and
). We have chosen
. As expected, the FM leads to more accurate results as the truncation order N goes to
. Note that our calculations have been performed with quadruple precision.
Figure 1 shows four normalized bound state wave functions as functions of X. We remark that there is a good agreement between analytical results and those obtained by the use of the FM, the number of terms in the series (17) and (19) being
.
3.2. Manning Potential
As an interesting application of the FM to a physical problem, we consider the MP that has been used in discussing vibrational energies of polyatomic molecules such as ammonia [8] , formamide [12] , cyanamide [13] and their deuterated species. In order to study one of the vibrational normal modes of
and
, Manning [8] proposed a potential defined by the expression
(46)
where
,
is the reduced mass of the molecule for the type of vibration considered; X is the distance from the nitrogen atom to the plane of the hydrogen atoms; and
,
and D are arbitrary constants. The SE for the vibration is
(47)
![]()
Figure 1. The normalized wave functions of the ground state, the first, fifth and sixth excited states contained within the HPTP described by the parameters
atomic units and
atomic units.
![]()
Table 1. Bound state energies (in atomic units) for the one-dimensional HPTP with
and
.
where E is the energy in cm−1. If we define
, we obtain the dimensionless Schrödinger Equation (5) with
,
,
and
. (48)
Following Manning [8] , we choose
(91.4),
(3261) and
for
.
Figure 2 shows the MP in cm−1 for both sets of parameters, as a function of x. This potential exhibits two minima and a barrier with maximum at x = 0. Although the barriers appear to be rather low, there are several energies between a minimum of the potential and the maximum of the barrier. We have calculated these energies by means of the FM. Our results are reported in Table 2 and Table 3, and compared with Manning’s ones [8] and those calculated by the use of the Wronskian method (WM) [14] . The remarkable agreement between the results of the two completely independent approaches shows that the present calculation is sufficiently accurate. Note that
is defined by
.
4. Application to the Gaussian Potential Well
As another interesting application of the FM, we consider the one-dimensional SE for the attractive Gaussian potential
,
(49)
i.e.
. (50)
![]()
Figure 2. Manning potential for NH3 and ND3.
![]()
Table 2. Energies of the Manning potential for NH3.
![]()
Table 3. Energies of the Manning potential for ND3.
The GPW is not a long range potential, because it falls off faster then
. However, it has a crucial advantage over the widely used “finite square well” potential in that it is continuous throughout the entire range
, whereas the finite square well goes to zero discontinuously. Furthermore, the Gaussian well of the form (49) has been used by Bardsley and Comella [15] for describing model neutral atoms with a few bound states.
It is worth noting that by an estimation based on the WKB method, the number of bound states supported by the potential (49) is approximated by [16]
(51)
where
represents the floor, which for positive numbers is simply the integer
part. But so far, to the best of our knowledge, exact analytical forms of the bound state energies and wave functions of this potential have not been reported. Therefore, it is of considerable interest to find a good approximation for the solution of the SE (50) which can be rewritten as
(52)
by changing variables from X to
.
The approximation solution we propose here relies on approximating the Gaussian function
by a potential of type (1). More precisely, we write
(53)
where
are adjustable parameters and K is a positive integer.
In order to show that the above approximation for the Gaussian function is suitable, we choose K = 8 and impose α = 0.35. We then discretize the problem in the interval
and evaluate the function
at
(for
) where p is the number of mesh points, h is the step size, and
and
are the minimum and maximum values of the variable
. We finally use the maple 18 Fit function to calculate the
coefficients. With
and
, we find:
(54)
Using these parameters, we plot the variations of
and
with
. We also consider the difference between the two functions, i.e.
.
It is obvious from Figure 3 that the approximation (53) is a very good one.
and
seem to coincide because the difference between them is of order 10−6 and hence very small.
By inserting this approximation in Equation (52) and then changing variables from
to
, we obtain the dimensionless Schrödinger Equation (5) with
end
,
. (55)
In Table 4, we present bound state energies obtained with the FM for
and
atomic units. This table contains also numerical results
obtained with the aid of the exact Hamiltonian diagonalization on the finite-real basis
where
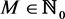 ,
,
. (56)
,
,
. (56)
![]()
Table 4. Bound state energies of the Gaussian potential well for
atomic units and
atomic units.
![]()
Figure 3. Plots of the Gaussian function (
), its approximation (
) and the difference between them (
).
We have chosen
as the number of basis functions,
as the order of the associated Lengendre polynomials intervening in Equation (56), and
. It is clear that our results are in good agreement with those obtained by means of the exact Hamiltonian diagonalization.
5. Conclusion
We have shown that the application of the Fröbenius method to the class of symmetric hyperbolic potentials of the form
allows an easy determination of the bound state energies and wave functions. The bound state energies associated with these potentials have been obtained numerically as zeros of a function, calculated from its power series representation. Since the potential
is even, the problem of computing its spectrum has been split into two calculations, dealing respectively with odd and even states. In order to demonstrate the performance of the FM on the potentials
, we have considered two special cases, namely the case of the HPTP which is an exactly solvable potential, and the case of the MP suggested by several authors to study polyatomic molecular vibrations. The numerical and analytical results presented in this work show that our results are sufficiently accurate and that our family of potentials can be used to model the GPW of the form
by suitably choosing the values of
, K and the
coefficients.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.