Nuclear Electromagnetic Generator: Mathematical Model on Toroidal Vacuum Scheme ()

1. Introduction
Presented work is related to research of the generation phenomenon of increasing external electromagnetic energy attached to rapidly increasing velocity (density) of passing for internal process of the chain nuclear fission reaction. Cascaded development of the chain nuclear fission reaction leads then to the vigorous intensification of external induced electric current and electromagnetic field. Besides the scenario of development for directional high-speed motion of increasing numbers of charged products of the fission may serve a basis for the creation of superpowerful energetical nuclear generators and electromagnetic power designs and accelerators of varied sorts particles also (see works [1] [2] [3] ).
Properly from the physics of considered process the nuclegens transform kinetic energy of charged products of the fission (splinters and anougher particles) immediately into electroenergy, as distinct from nuclear reactors, where only part of thermal energy of fission products transforms into electroenergy. It is clear that nuclegens according to own power potentials extremely powerfully will be surpassing analogous potentials of modern nuclear reactors.
Principled scheme of nuclear generator presents the vacuum toroid with uniformly wound external conductive spiral. Along all over ring the circular shields are installed from fissionable radioactive substance into internal hollow part of nuclegen. In the present case shields fulfil the role of fuel pins at usual nuclear reactor. In absence of moderator the controlled process of nuclear chain fission is realized at the expense of controlled turn of shields around own axes of revolution. Obviously that the change of shields position concerning the general neutron-fragmentation stream leads to the immediate change of the course of fission process.
Intervals between of shields are choosen from counting, firstly, of effectively increasing passing of the chain fission reaction and, secondly, of enough complete run of splinters and another fission products (within beginning of active recombination and neutralization of charges). Of course, it is possible and another just like engineering variants of concentration of fissionable substance into toroidal vacuum generator which lead to controlled intensification or weakening of the nuclear fission process.
Just one more comment. It concerns making of nuclear resonator for directional motion of charged particles. As a such resonator may serve in itself fuel shield if one of sides will be the reflector (the moderator) for positively charged fission splinters (particles), and another, opposite side―for negatively charged fission splinters (particles). Finally, it is possible variant with one reflector on boundary shield surface; variant when the voltage is given on surface of shield and so on.
Sections 2 - 5 are devoted to the description of characteristics of electromagnetic field for the toroidal nuclegen. In Section 2 Maxwell’s equations are used for the notion of general motion picture of charged particles. In Section 3, the transformation of Maxwell’s equations is realized for the forming wave equations. Section 4 is devoted to the description of fading regime of external electromagnetic field by the switching-off field sources. In Section 5, the calculation of parameters for electromagnetic fields is conducted.
2. General Description of Electromagnetic Process Maxwell’s Equations
Further for simple of text record we shall not be distinguish the vector and scalar values between of itself, so far as from the context of presented analytical expressions it is becoming clearly which value (vector or scalar) is meant. Suppose that on external winding of toroid the electric exterior current is given with amperage I0 and density j0, exciting directed electromagnetic field within of nuclear generator. We shall be characterizing this external field by means of strength E0 and electric induction D0 (for electric field), of strength H0 and magnetic induction B0 (for magnetic field). In considered case for the field at vacuum we have
where
F/m (Farad/metre)―electric constant,
Hn/m (Henry/metre)―magnetic constant.
In a position when shields are closed and the process of chain fission is started the uncrowded intervals between them are filled with multitude of charged high-speed particles and fission splinters. In essence, enough strong external electromagnetic field
with current
is necessary only for their initial interdirected accelerated motion along toroid. Besides, induced in external winding the current
and the electromagnetic field
discover also (as it will be shown below) exponentional intensive avalance-like growth with growth of neutrons number and free charges under exponentional law. This is phenomenological aspect of a matter. We attemp to envelop foregoing in analitical expressions.
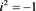
Make use of general macroscopic Maxwell’s equations for variable electromagnetic field
are written in differential (local) form:
(1)
with boundary conditions on G from a certain region W, namely
, where
is the density of fully current, jd is the density of displacement current, j is the density of conductivity current, ρ is the
volumetric charged density,
is the conductivity current,
is the displacement current, S is a surface. Owing to vector identity
we have
. If in this relation trade places operators div and
then taking into account
we obtain the equation of continuity
Note also the connection between j and
, where σ is specific conductivity. In general system of Maxwell’s Equations (1) according to the principle of superposition we have the addition of external and internal electromagnetic fields:
Suppose that as a result of chain nuclear fission reaction in the time moment t in “free” toroidal volume there is some finite number K of “free” charged particles and splinters (light and heavy) of different sign and N neutrons. By interdirected longitudinal motion into external electromagnetic field of positive and negative particles there are created “superthin” currents of convective form with densities
, where
is volumetric density of charge allocation of i-th particle (splinter),
is its velocity. i.e. resultant (at the first approximation) current inside of nuclear toroidal generator is characterized by the density
(2)
It is necessary to add that on the each charged i-th particle is effected, as is known, the Lorenz’s force into external electromagnetic field
(3)
where
is charge of i-th particle (splinter), moreover according to Gaussian theorem for the volume V with surface S we have
As a result of the action of Lorenz’s force (3) the partiale trajectory inside of toroid will be tighten up in spiral. General picture motion of charged particles and another products of fission nuclear into powerful directed increasing electromagnetic field must present, apparently, longitudinal intertwisting with speed-up the spiral electromagnetic cord inside of toroidal nuclegen in itself.
3. Electromagnetic Modelling Transformation of Maxwell’s Equations
Convert Maxwell’s equations for vacuum (1) and use standard methods of the vector differential analysis trying to solve system (1) on magnetic (H) and on electric (E) components. We have from the second group of equations
(4)
So the field E is determined with the aid of Equation (4) owing to known H. Further for any vector A we avail identities
(5)
where Δ is Laplace’s operator. We obtain from Equation (4) (
):
(6)
Substitute the expression for
from the first group of Equation (1) at Equation (6). Taking into account correlations (5) we have the wave equation for H:
(7)
Analogously we obtain the wave equation for E:
(8)
4. Fade Regime of External Field by the Switching-Off of Field Sources
We should be considering that charged electromagnetic cord in toroid presents in the aggregate the conductor situated into electromagnetic field. Then by instantaneous switching-off of field sources the field would not disappear but it would be exponentionally in the time fading according to spatial-evolutionary Equations ((7) and (8)). Following to known solution methods of problems of mathematical physics we should be solutions of Equations ((7) and (8)) searching correspondingly in the form
(9)
with constant coefficients
; here
are cartesian spatial variables, t is the time. We obtain equations for vector functions
:
(10)
(11)
Equations ((10), (11)) have not equal to zero solutions satisfying boundary conditions under the certain set of eigenvalues
.
Elucidate the character of alteration for numbers
. Carry out this analysis as an example
. Take Equation (10) in the form
and scalar multiply vector-line 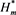 on this equation (here * above is the transposition sign). We obtain after integration over total space
on this equation (here * above is the transposition sign). We obtain after integration over total space
 (12)
(12)
Reality and positivity of value  follow with evidence from equality (12). This condition answered numbers:
follow with evidence from equality (12). This condition answered numbers:
1) real , for which
, for which ;
;
2) complex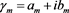 , where
, where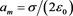 ,
,  ,
, 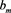 are arbitrary real numbers.
are arbitrary real numbers.
Quite analogous opinions may be adduce for numbers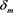 , if to proceed from Equation (11). In either case we have to deal with dynamic process which solutions (9) fading exponentionally in the time. At last, we set the distribution of field in initial time moment with the aid of functions
, if to proceed from Equation (11). In either case we have to deal with dynamic process which solutions (9) fading exponentionally in the time. At last, we set the distribution of field in initial time moment with the aid of functions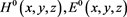 . Expand their into Fourier series on full systems of mutually orthogonal vector functions
. Expand their into Fourier series on full systems of mutually orthogonal vector functions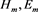 :
:
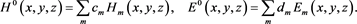
Then the general solution of problem about fading of variable electromagnetic field may be written in the form
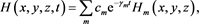
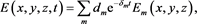
where cm and dm are some numerical coefficients.
5. Calculation of Electromagnetic Fields
At next stage of electromagnetic modelling, we include quasistationary monochromatic external field 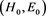 with frequency w and internal field on charges
with frequency w and internal field on charges 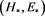 counting that as a result of controlled chain nuclear reaction into toroidal generator there is established process of fission (the certain finite number K of charged particles and charged splinters of fission and N of neutrons). Calculate suitable fields.
counting that as a result of controlled chain nuclear reaction into toroidal generator there is established process of fission (the certain finite number K of charged particles and charged splinters of fission and N of neutrons). Calculate suitable fields.
At first we calculate the field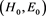 . In quasistationary case the dependence of every value from the time given by means of the factor
. In quasistationary case the dependence of every value from the time given by means of the factor![]() . Then transforming Maxwell’s Equation (7) assumes the form
. Then transforming Maxwell’s Equation (7) assumes the form
![]() (13)
(13)
where![]() . We can obtain
. We can obtain ![]() from the equation
from the equation ![]() ignoring displacement current in investigated quasistationary field and using Equation (8) we can write for E0:
ignoring displacement current in investigated quasistationary field and using Equation (8) we can write for E0:
![]() (14)
(14)
Wave Equations ((13), (14)) lead to general Bessel’s equations. In our study is considered that toroidal nuclear generator is closed circular solenoid with cylindrical conductive surface on which flows the surface current of conductivity. For such hollow conductor solutions of Equations ((13), (14)) yield known surface skin-effect [4] on Bessel’s functions for corresponding equations.
We agree in this time that the current into external winding is direct and has a value I0. In this case we can write
![]() (15)
(15)
from which, specifically, the existence of constant electric field E0 and its potentiality follows inside of conductor. At condition that ![]() follows the harmonicity of potential electric field.
follows the harmonicity of potential electric field.
For solution of second group of Equations (15) as usual is introduced the vector potential A so that![]() ,
,![]() . When
. When ![]() we have
we have
![]()
Then taking into account the identity (5) write for A the Poisson equation:![]() , from which we find
, from which we find
![]() (16)
(16)
where r is distance from observation point to volume element dV; r in numerator of second formula (16) is radius-vector, incidentally this formula expresses the law of Biot-Savart. Use relations (16) and calculate the field H0 for toroid on which direct current I0 flows in cylindrical coordinates![]() . Magnetic field outside of toroidal solenoid
. Magnetic field outside of toroidal solenoid ![]() And inside
And inside
![]()
where n is number of wire spirals.
Now proceed to the calculation of field ![]() supposed that this field presents the action result of totality of internal charged currents (2) in neglect of their action between itself where K is constant number. Certainly, here the constancy of K and some other values is understood in enough rough and relative sense. Suppose
supposed that this field presents the action result of totality of internal charged currents (2) in neglect of their action between itself where K is constant number. Certainly, here the constancy of K and some other values is understood in enough rough and relative sense. Suppose ![]() is full current on K moving charges in vacuum:
is full current on K moving charges in vacuum:
![]() (17)
(17)
i.e. moving with velocity ![]() the charge
the charge ![]() is equivalent in accordance with expressions (17) to linear current
is equivalent in accordance with expressions (17) to linear current ![]() is induced by i-th particle. Further, we have taking into account relation (2):
is induced by i-th particle. Further, we have taking into account relation (2):![]() . Particles with different on sign charges, as was said earlier, move in opposite directions along of nuclear generator on weakly twisted spirals under the influence of increasing resultant field
. Particles with different on sign charges, as was said earlier, move in opposite directions along of nuclear generator on weakly twisted spirals under the influence of increasing resultant field![]() .
.
It is easily establish the direction of magnetic induction vector ![]() in observation point which is tangent to magnetic induction lines created by spot charge
in observation point which is tangent to magnetic induction lines created by spot charge ![]() in vacuum:
in vacuum:
![]() (18)
(18)
In the numerator of formula (18) ![]() are vectors, moreover
are vectors, moreover ![]() is velocity vector of the point with charge
is velocity vector of the point with charge ![]() and
and ![]() is radius-vector from this point to the observation point. Hence we obtain the expression for the module of vector
is radius-vector from this point to the observation point. Hence we obtain the expression for the module of vector![]() :
:
![]()
where α is the angle between of vectors ![]() and
and![]() . Note also the unidirectionality of vectors
. Note also the unidirectionality of vectors ![]() and
and ![]() for i-th and j-th particles if charges
for i-th and j-th particles if charges ![]() and
and ![]() have different signs and opposite directions of motion. From this important circumstance in accordance with the superposition principle follows the relation
have different signs and opposite directions of motion. From this important circumstance in accordance with the superposition principle follows the relation
![]() (19)
(19)
Then we determine ![]() due to value
due to value ![]() (19).
(19).
6. Conclusions
In this article, some questions of mathematical modelling of drastic directional electromagnetic fields generation on toroid as a result of nuclear chain fission process find own reflection. Calculation of electromagnetic field characteristics in external winding of the toroid for various regimes of nuclegen work is produced. On the base presented here general mathematical model of the nuclear electromagnetic generator functioning may be constructed the model of nuclear kinetic process for charged particles and charged splinters into the nuclegen. Besides, may be created the model of neutron kinetics for the nuclegen also. That’s exactly contained the significance and the novelty of produced results for the future purpose of the study.
Items [1] [4] are published in Russian except [2] [3] .