
1. Introduction
In 1887, Michelson and Morley performed the well-known Michelson-Morley experiment to determine the speed of the earth relative to that of the luminiferous ether [1] [2] , which was considered the fundamental substratum of space and believed to be the medium of light propagation [3] . The idea of the experiment can be summarized as follows: “The motion of the earth in the ether at velocity v generates an ether wind with the same velocity; therefore, if we succeed in measuring the effect of the ether wind on light motion, it will serve as a strong evidence for the existence of the ether.”
The null result of the Michelson-Morley experiment is considered strong evidence against the ether theory [4] and is unexpected according to Galilean physics. In 1892, Lorentz first explained this null result in an attempt to conserve the ether theory; he suggested that the length of a body/object in the direction of motion contracts by an amount equal to
(the Lorentz factor) because of a postulated similarity between molecular cohesion forces and electrostatic forces [5] . The Lorentz transformations are a set of mathematical equations [6] used to correlate space and time coordinates of a moving system to determine the space and time of another system, when two observers (each in either system) are moving relative to each other. The Michelson-Morley experiment can be explained by these transformations; the length of an object along the direction of motion contracts (by a factor equal to γ) [7] while transforming to a moving frame. Consequently, the speed of light is identical in all frames, thus yielding the null result of the Michelson-Morley experiment.
Following this, in 1905, Einstein posited the non-existence of the absolute medium and introduced the “special relativity” theory, which is based on two postulates: first, the laws of electrodynamics and optics are valid for all frames of reference; second, the speed of light is constant regardless of the motion of the light source [8] , Einstein deduced the Lorentz transformation from these two postulates. Consequently, he suggested that the length of moving bodies contracts along the direction of their motion and that the bodies undergo time dilation [9] [10] ; therefore, the result of the Michelson-Morley experiment is negative. Special relativity introduces a different system in which space and time are not absolute for all inertial frames [11] . Rather, they are relative to the frame of reference [12] unlike in the Newtonian world, where space and time are absolute for all inertial frames. The purpose of this paper was to show that time dilation and its results (e.g. length contraction) can be one of the implications of Newtonian time if we postulate a specific hypothesis related to the geometry of Newtonian space.
1.1. Postulate
The following postulate considered herein:
-Newtonian space is sloped, or in other words; the univere is sloped (Figure 1).
![]()
Figure 1. (a) It shows straight Newtonian space where space represented horizontally and time represented vertically while (b) shows sloped Newtonian time where space represented as sloped horizontal lines and time represent as straight vertical lines.
1.2. Research Summary
This study introduces the space-time continuum as an emerging phenomenon based on the absolute nature of space and time and the slope of space. To prevent confusion, this study provides a new analysis on the vertical motion of light in moving frames in case of slope of moving systems related to each other. A new theory on this concepts is also established without interfering with previous experimental work [13] [14] [15] . According to the mentioned postulate, new dimensions are created, these dimensions are referred to as reverse space- time, which is similar to the motion of cars along a hill in races, where cars suffer from resistance to move forward or slid backward during their motion to forward. The distance that the cars regress and the time that the cars delay to move forward consider the dimensions within which the cars exist. This study has the following idea: the absolute space supposed by Newton looks like a hill, this reflects on moving frames by making it sloped and tilted also with respect to observers at rest, the moving frames are also suffer from resistance to move forward in absolute space and time; hence, it reverse slightly backward in space and time, the motion of light during motion of the frame to forward and backward need to be considered (Figure 2).
![]()
Figure 2. The moving car is sloped and slided due to slope of Newtonian space.
2. Methods
The theoretical analysis of emergence of time dilation from Newtonian time was performed in accordance with the constancy of the speed of light, regardless of the light source motion.
3. Results
I find there are many results can be obtained based on slope of Newtonian space or slope of the universe.
3.1. Space of Moving Frames is Sloped with Respect to Space of Stationary Frame of Reference
The slope of Newtonian space or the universe makes the moving frames experience slope where space of the moving frame become sloped with respect to space of the stationary frame of reference that it exists at rest so it cannot experiences slope property of Newtonian space like moving frames (Figure 3).
![]()
Figure 3. The moving frame (the red one) is observed as sloped (the blue one) with respect to the observer in a stationary frame that is colored black.
3.2. Re-Calculation of the Distance That Light Travels between Two Relative Moving Systems According to Absolute Time and Slope of Newtonian Space
This section describes the calculation of the difference,
, between the distances that light travels vertically in frames
and
(frames in a uniform relative motion) according to the presence of a universal time between the two frames. In the next section, I will show and explain where light travels along this distance,
and explain the physical meaning or the physical name of
. Suppose that a vertical light beam is emitted in the
direction in frame
. Thus,
, which represents the distance that the light beam travels vertically in frame
(Figure 4), can be given in the presence of absolute time,
, as follows:
![]()
Figure 4. The red vertical line refers to the light motion in the moving frame
that is colored red from perspective of the observer of the same frame who is colored red, while the yellow sloped line refers to the light motion in the sloped
(that is colored blue) from perspective of the stationary frame of reference
that is colored black (observer at rest).
(1)
(2)
The transformed distance,
, which refers to the distance that light travels in frame
, from the perspective of the observers in frame
will not be represented mathematically as a triangle’s string because according to the mentioned postulate, space of the moving frame
is sloped with respect to the observers of the stationary frame
, therefore the transformed distance,
, will be represented mathematically as a triangle’s rib while the distance,
, will be represented mathematically as a triangle’s string. Accordingly the transformed distance,
, can be given as follows in the presence of a universal time (absolute duration):
(3)
(4)
The difference between the distances (
) that light travels vertically in frames
and
is given as follows according to Equations (2)-(4):
(5)
(6)
We obtain the three following important equations based on the mathematics in this section:
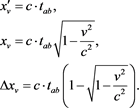 (7)
(7)
3.3. Space of Moving Frames Is Revered with Respect Observers at Rest
If space is absolute in nature as Newton supposed, it should be determined why light travels vertically a shorter distance
in frame
compared to that
in frame
and where light travels along the distance
determined in the previous section. According to the mentioned postulate, which states that “Newtonian space is sloped,” the moving frame
slightly slides backward with respect to the observers in the stationary frame
. This divides or classifies the distance that the light travels vertically in frame
, from the perspective of the observers in frame
into two kinds with two different directions: the distance that the light travels or progresses to forward
and the distance that the light travels or regresses to backward
or
. The sum of the two distances that the light travels vertically to backward and forward in frame
, from the perspective of the observers in frame
is equal to the distance
that the light travels vertically in frame
from the perspective of the observers in the same frame
(Figure 5).
![]()
Figure 5. The distance that the light travels vertically during motion of the blue frame
to forward
and the distance that the light travels vertically during motion of the same frame to backward
are equal to the distance
that the light travels vertically in the red frame
from the perspective of the observers in the same frame
.
By this explanation, the distance that the light travels vertically is the same for all the frames of reference regardless the motion:
(8)
(9)
where,
(10)
(11)
while,
(12)
(13)
where
is the Lorentz factor. This phenomenon is named herein as “space reversal,” which refers to the reversal of the space of moving bodies with respect to a stationary frame of reference because of the slope of Newtonian space.
3.4. Time of Moving Frames Is Reversed with Respect to Observers at Rest
As mentioned in the previous section, the moving frame
slightly slides backward because of the slope of space, thereby leading to the reversal of the time of frame
with respect to the observers in frame
. The reversed time
of frame
as measured in frame
can be derived using the following equations if the backward distance that light reverses in frame
as measured in frame
is
:
(14)
(15)
The reversed time of the moving frame
with respect to the observers in frame
is determined using Equation (15). This phenomenon is named here as “time reversal” (Figure 6), which refers to the reversal of the time of moving bodies with respect to a stationary frame of reference because of the slope of space. According to Equation (15), the reversed time
of the moving bodies is relative depending on the velocity of the moving bodies from the perspective of the stationary observer. This finding is different from the nature of time or progressing time
that is absolute for everyone everywhere (independent of the motion of the bodies). Therefore, “time moves forward absolutely (as Newton suppose) and backward relatively.”
![]()
Figure 6. The universal time of two different moving frames (
) is reversed with respect to an observer at rest by different values (
) depending on the velocity of the moving frames, where
.
3.5. Calculation of the Elapsed Time in the Moving Frames with Respect to Observer at Rest
Like a car that moves slowly because it is climbing a hill, the time of the moving bodies moves slowly because of the slope of space. The total elapsed time (
) in the moving frame with respect to the stationary frame of reference can be calculated as follows:
(16)
(17)
According to Equation (17), the clock in the moving frame moves slowly with with respect to the observers in the stationay frame
where the stationary clock exceeds the moving clock. This phenomenon is known as “time dilation” and it is the most important result of special relativity. This section shows how the result of “time dilation” can be obtained according to the “reversal of time” phenomenon. “Time in moving frames moves forward absolutely (as Newton suppose) and backward relatively, where the final result refers to the dilation of the elapsed time in the moving frames with respect to the stationary frame of reference depending on the velocities of the moving frames as measured in the stationary frame of reference (as Einstein suppose)”.
3.6. Dimensions of the Universe
We describe the classification of the dimensions of the universe in this section.
3.6.1. Newtonian Dimensions-3D “Group. A”
a) First dimension “length”; absolute length, in its own nature, without regard to anything external, remains always similar. The absolute length
can be determined as follows:
(18)
b) Second dimension “width”; width is relative with respect to stationary frame of reference as a result of slope of Newtonian space. The relative width
can be determined as follows:
(19)
c) Third dimension “height”; height is relative with respect to stationary frame of reference as a result of slope of Newtonian space. The relative height
can be determined as follows:
(20)
d) Time; Absolute, true and mathematical time, of itself, and from its own nature flows to forward equably without regard to anything external, so it can’t be considered as a dimension as it moves to forward regularly for everyone everywhere. The absolute time
can determined as follows:
(21)
Thus, three dimensions of space are obtained while time can’t be considered as a dimension. The three dimensions of space are called “Newtonian Space” that is always sloped. The height with width form a new continuum called the “width-height continuum.”
3.6.2. Reversed Dimensions-4D “Group. B”
As a result of slope of Newtonian space, the moving frame become sloped with respect to observers at rest and thus the space and time of moving frame
become slightly reversed to backward with coordinates
from perspective of stationary frame of reference
, the reversed space-time can be determined as follows:
(22)
where,
(23)
Thus, three dimensions of the relative reversed space and one dimension of the relative reversed time are obtained. The four dimensions of space and time are called “reversed space-time.”
3.6.3. “Group. A” & “Group. B” with Respect to Stationary Frame of Reference
The final result of “Newtonian space” and “Reversed space-time” can be obtained as follows:
a) Regarding to the length, the total distance that light travels longitudinally
through two dimensions; Newtonian length
and Reversed length
in frame
is less than the distance that light travels longitudinally in frame
that is
:
(24)
And as
We find
(25)
b) Regarding to the width, the total distance that light travels transversely
through two dimensions; Newtonian width
and Reversed width
in frame
is equal to the distance that light travels transversely in frame
that is
:
(26)
By Equations ((19) and (22)), we can get,
(27)
Thus the total distance
that light travels transversely is the same for all the frames of reference.
c) Regarding to the height, the total distance that light travels vertically through two dimensions; Newtonian height
and Reversed height
in frame
is equal to the distance that light travels vertically in frame
that is
:
(28)
By Equations ((20) and (22)), we can get,
(29)
Thus the total distance
that light travels vertically is the same for all the frames of reference.
d) Regarding to duration, the duration or the total time
taken by light at the moving frame through two dimensions; Newtonian time
and Reversed time
in frame
is more than the time taken by light in frame
that is
:
(30)
By Equations ((16) and (17)), we can get,
(31)
Thus the duration taken by light at the moving frames dilated with respect to the stationary frame of reference.
Accordingly length of moving frames is decreased and time move slowly with respect to stationary frame of reference while width and height of moving frames are the same for everyone everywhere (Table 1 & Table 2) and by this method; Lorentz transformation obtained that are:
(32)
![]()
Table 1. Stationary observer in frame
records the events in the moving frame
with coordinates
.
![]()
Table 2. Emergence of relativity from absoluteness regarding length and time & emergence of absoluteness from relativity regarding height and width.
3.7. Calculation of Slope of Newtonian Space
In this section, we aimed to calculate the value of slope of Newtonian space of the moving frame with respect to space of the stationary frame of reference (Figure 7) as the following equations show:
(33)
(34)
(35)
![]()
Figure 7. Angle of slope
of the moving space with respect to the stationary space.
(36)
(37)
(38)
(39)
By Equations ((34), (36), (38) and (39)), we can get the angle of slope of the moving frame
as,
(40)
From Equation (40) the slope of space of a moving frame with respect to space of an observer who exists at rest is given by,
(41)
According to the previous equation, we find that space of moving frames is sloped positively with respect to space of the stationary frame of reference.
4. Discussion
I find there is a simple method that by it space-time continuum can be emerged from absolute space and time that is denied after special relativity. If absolute space is sloped, time dilation and its implications (length contraction) will be the result. The study explains time dilation as follows: the moving frames experiences resistance while progressing to forward; thus, light slides slightly backward during its forward motion, leading to a delay in moving clocks with respect to stationary clocks, where the second in a stationary frame of reference precedes the second in the moving frames. Referring to this phenomenon as time dilation is not accurate because time runs regularly everywhere. Therefore, it is better to refer to it as time delay where time in moving frames moves forward absolutely (as Newton suppose) and backward relatively.
5. Conclusion
The previous sections show that Newtonian space is sloped and the value of
![]()
Figure 8. The angle of slope
of the moving space with respect to the stationary space depends on speed of Newtonian space toward Newtonian time and velocity of the moving frame.
slope is relative and changed depending on velocity of the moving frame with respect to the observer at rest, so I conclude that Newtonian space (the universe) is in motion where its horizontal axis is changed from time to time; in other words, Newtonian space is movable towards axis of Newtonian time where slope of Newtonian space that the moving frame experience. It depends on velocity of the moving frame and speed of axis of Newtonian space itself toward axis of Newtonian time, that speed equals speed of light (Figure 8).
Acknowledgements
I would like to thank Editage (https://www.editage.com/) for the English language editing and publication support.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.