R(D) Definition Domain Deriving of Limited Distortion Source Coding With Different Sources ()
1. Introduction
From the point of view of information processing, no distortion source coding is entropy preserving. And the entropy preserving coding is not always necessary. Such as the human eyes to accept the visual signal, then there is no need to carry out the distotion-free entropy coding. But entropy preserving coding is not always possible. For example, when the continuous signal is subjected to digital processing, it is impossible to fundamentally remove the quantization error. At this point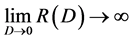 . Although the relative entropy of the continuous source is limited, the amount of information is infinite [1]. But the actual channel always has interference, and its capacity is limited, so the distortionless transmission of this continuous information is impossible. Only when certain distortion is allowed, the value of
. Although the relative entropy of the continuous source is limited, the amount of information is infinite [1]. But the actual channel always has interference, and its capacity is limited, so the distortionless transmission of this continuous information is impossible. Only when certain distortion is allowed, the value of 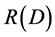 is finite, and the transmission is possible.
is finite, and the transmission is possible.
Reducing the rate of information is beneficial to transmission and processing, so it is necessary to perform entropy compression coding. Therefore, it is necessary to introduce the source coding with limited distortion. 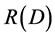 is a very important parameter in the source code is the information rate distortion function [2] [3]. In the case of allowing a certain degree of distortion, the rate-distortion function of
is a very important parameter in the source code is the information rate distortion function [2] [3]. In the case of allowing a certain degree of distortion, the rate-distortion function of 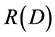 the source can be used as a measure of the performance of various compression coding methods. It is generally assumed that the minimum value
the source can be used as a measure of the performance of various compression coding methods. It is generally assumed that the minimum value 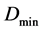 of the coding average distortion is 0 and the maximum value
of the coding average distortion is 0 and the maximum value 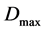 is the minimum distortion value of
is the minimum distortion value of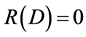 , that is the definition field of the
, that is the definition field of the 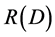 function is
function is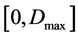 . In fact, in many cases,
. In fact, in many cases, 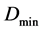 is not necessarily zero [4] [5], its value is related to the single symbol distortion function. Only when the distortion matrix has at least one zero element in each row, the average distortion of the source can reach zero. In this paper, the upper and lower bounds of the definition domain of
is not necessarily zero [4] [5], its value is related to the single symbol distortion function. Only when the distortion matrix has at least one zero element in each row, the average distortion of the source can reach zero. In this paper, the upper and lower bounds of the definition domain of 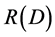 are deduced, and the upper and lower bounds of the definition domain of
are deduced, and the upper and lower bounds of the definition domain of 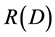 under different source and different distortion function are given. In this way, we can further improve the limitless source coding theorem.
under different source and different distortion function are given. In this way, we can further improve the limitless source coding theorem.
2. The Infer of Domain Definition of the Information Rate Distortion Function 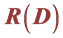
The information rate distortion function 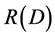 independent variable
independent variable 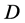 is the average distortion caused by a limited information source coding algorithm. The average distortion allowed is the upper limit of the stipulated average distortion
is the average distortion caused by a limited information source coding algorithm. The average distortion allowed is the upper limit of the stipulated average distortion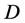 . The definition domain question of information rate distortion function is that the minimum and maximum values of average distortion
. The definition domain question of information rate distortion function is that the minimum and maximum values of average distortion 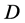 are studied when the information source and the distortion function are known. The value of
are studied when the information source and the distortion function are known. The value of 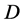 must satisfy the fidelity criterion
must satisfy the fidelity criterion
![]() (1)
(1)
The average distortion ![]() is determined according to the statistical properties of a information source
is determined according to the statistical properties of a information source![]() , Statistical property
, Statistical property![]() , coding mapping function
, coding mapping function ![]() and distortion function
and distortion function![]() , that is [1]
, that is [1]
![]() (2)
(2)
2.1. The Defined Domain Lower Bound of Information Rate Distortion Function ![]()
The mathematical expectation of nonnegative real numbers ![]() is
is![]() , therefore,
, therefore, ![]() is a nonnegative real number, with a lower limit of 0, so that the permissible lower bound of the average distortion
is a nonnegative real number, with a lower limit of 0, so that the permissible lower bound of the average distortion ![]() must be 0, that is
must be 0, that is![]() , this is the case where no any distortion is allowed. As for whether the permissible average distortion can reach its lower limit value of 0, it is related to the distortion function of a single symbol. When solving the minimum mean distortion
, this is the case where no any distortion is allowed. As for whether the permissible average distortion can reach its lower limit value of 0, it is related to the distortion function of a single symbol. When solving the minimum mean distortion ![]() of the information source, for each
of the information source, for each![]() , find a corresponding
, find a corresponding ![]() that makes the minimum
that makes the minimum![]() , and the corresponding
, and the corresponding ![]() minimum values for different
minimum values for different ![]() are also different. This is equivalent to finding a smallest
are also different. This is equivalent to finding a smallest ![]() in each line of the distortion matrix, and the minimum
in each line of the distortion matrix, and the minimum ![]() of each line is different. The mathematical expectation of all these different minima
of each line is different. The mathematical expectation of all these different minima ![]() is the minimum mean distortion of the information source [1], that is
is the minimum mean distortion of the information source [1], that is
![]() (3)
(3)
It can be seen by (3) formula, When each line of the distortion matrix has at least one zero element, the average distortion of the information source can reach the lower bound value, otherwise ![]() must not be equal to zero. When
must not be equal to zero. When![]() , that is, the information source does not allow any distortion to exist, which is equivalent to noiseless channels. At this point, the amount of information transmitted by the channel is equal to the entropy of the information source. That is
, that is, the information source does not allow any distortion to exist, which is equivalent to noiseless channels. At this point, the amount of information transmitted by the channel is equal to the entropy of the information source. That is
![]() (4)
(4)
If the formula (4) is established, each line in the distortion matrix has at least one zero, and each column can have at most one zero. Otherwise, ![]() can be less than
can be less than![]() , which means that the information source symbols are concentrated, and some symbols can be compressed and merged without any distortion.
, which means that the information source symbols are concentrated, and some symbols can be compressed and merged without any distortion.
2.2. The Defined Domain Upper Bound of Information Rate Distortion Function ![]()
For the maximum average distortion of the information source![]() , the smaller the required compression rate, the greater the tolerance distortion. When
, the smaller the required compression rate, the greater the tolerance distortion. When![]() , the corresponding average distortion is maximal,
, the corresponding average distortion is maximal, ![]() is the upper bound of the domain of the function
is the upper bound of the domain of the function ![]() definition. Since the information rate distortion function
definition. Since the information rate distortion function ![]() is the minimum of average mutual information
is the minimum of average mutual information![]() . So when
. So when![]() , the minimum value of the average mutual information at that time is equal to 0, this moment
, the minimum value of the average mutual information at that time is equal to 0, this moment![]() . Because
. Because ![]() is a nonnegative function,
is a nonnegative function, ![]() is also a nonnegative function. When
is also a nonnegative function. When![]() ,
, ![]() can only be equal to 0. Therefore, the upper bound
can only be equal to 0. Therefore, the upper bound ![]() of the
of the ![]() defined domain is the minimum value for all
defined domain is the minimum value for all ![]() that satisfy
that satisfy![]() .
.
![]() equivalent input
equivalent input ![]() and output
and output ![]() statistical independence, which means that any information sent not received at the receiving end, equivalent to the information source does not send any information, or transmission of information source symbol information rate can be compress to 0. Therefore,
statistical independence, which means that any information sent not received at the receiving end, equivalent to the information source does not send any information, or transmission of information source symbol information rate can be compress to 0. Therefore, ![]() has nothing to do with
has nothing to do with![]() . That is
. That is
![]() (5)
(5)
By Equation (5), ![]() can be solved.
can be solved.
![]() (6)
(6)
From the Equation (6) can be observed, In![]() , you can find the
, you can find the ![]()
that minimizes the ![]() value. When
value. When ![]() corresponds to the
corresponds to the
![]() , and the rest of the
, and the rest of the![]() , the right of the formula is minimized. At this point, the upper Formula can be simplified into
, the right of the formula is minimized. At this point, the upper Formula can be simplified into
![]() (7)
(7)
Formula (7) is for different , using the input probability distribution![]() , the mathematical expectation of the
, the mathematical expectation of the ![]() is taken, the minimum of the mathematical expectation corresponding to the
is taken, the minimum of the mathematical expectation corresponding to the ![]() is taken as
is taken as![]() , at this point, making the
, at this point, making the ![]() is the corresponding output probability of the
is the corresponding output probability of the![]() , while the other
, while the other![]() .
.
Thus, the domain of definition ![]() can be defined as
can be defined as![]() .
.
2.3. Domain of the Different Sources Rate Distortion Function ![]()
The information source is n element equal probability distribution, the distortion is Hamming distortion
![]() (8)
(8)
Then the rate distortion function of the information source is [2]
![]() (9)
(9)
By the Equation (9), the value of ![]() and
and ![]() can be computed, the corresponding simulation diagram of
can be computed, the corresponding simulation diagram of ![]() based on MATLAB is shown in Figure 1.
based on MATLAB is shown in Figure 1.
For the information source of unequal probability distribution, the several typical information sources are considered, and the corresponding upper bound ![]() and lower bound
and lower bound ![]() are obtained by the above derivations as Table 1.
are obtained by the above derivations as Table 1.
3. Conclusion
In this paper, the upper and lower bounds of the definition domain of the information rate distortion function ![]() are deduced and analyzed. The information source type and the distortion function
are deduced and analyzed. The information source type and the distortion function ![]() determine the ex-
determine the ex-
![]()
Table 1. The upper and the lower bound of typical information source.
pression of the information rate distortion function ![]() and the upper and lower bounds of the definition domain. Ideally, we all think that the lower bound of the definition domain of the information rate distortion function
and the upper and lower bounds of the definition domain. Ideally, we all think that the lower bound of the definition domain of the information rate distortion function ![]() is 0, but in practical applications, it’s necessary to consider if the lower bound of the definition domain of
is 0, but in practical applications, it’s necessary to consider if the lower bound of the definition domain of ![]() can be taken as zero. Accurately speaking, the definition domain of
can be taken as zero. Accurately speaking, the definition domain of ![]() is
is![]() . The value of
. The value of ![]() is related to whether the transmission rate can reach the entropy of the source. Therefore, it is necessary to calculate the maximum information transmission rate
is related to whether the transmission rate can reach the entropy of the source. Therefore, it is necessary to calculate the maximum information transmission rate ![]() after the source coding, so as to solve all kinds of practical problems in information transmission. In this paper, by defining the precise deduction of the lower bound of the
after the source coding, so as to solve all kinds of practical problems in information transmission. In this paper, by defining the precise deduction of the lower bound of the ![]() definition domain, it is explained in detail whether or not it can get zero value, and under what conditions zero value can be reached. It further prefects the theory of distortion limited source coding, and it has practical significance for data compression and data transmission of real information source.
definition domain, it is explained in detail whether or not it can get zero value, and under what conditions zero value can be reached. It further prefects the theory of distortion limited source coding, and it has practical significance for data compression and data transmission of real information source.
Acknowledgements
This work was funded by National Natural Science Foundation of China―Re- search on no proportion coding cooperative transmission method based on dynamic antenna selection in large scale MIMO systems (61601170) and Henan Provincial Department of science and technology project―Study on wireless channel characteristics of bulk grain reactor (172102210230).