Evaluating Traffic Congestion Using the Traffic Occupancy and Speed Distribution Relationship: An Application of Bayesian Dirichlet Process Mixtures of Generalized Linear Model ()
1. Introduction
Speed is one of the important parameters in traffic flow analysis. Hence, understanding its characteristics is essential in the application of intelligent transport systems and for measuring the consistency of the traffic performance of a highway system. Furthermore, the speed distribution is useful in simulation and theoretical derivations regarding different traffic performance measures such as speed reliability and variability. The accurate estimation and prediction of speed are essential for traffic operators, planners, and traveler information systems [1] .
Several factors influence the distribution of the traffic speed on freeways. These factors can be grouped into time-variant and time-invariant factors. The time-invariant factors include road geometric characteristics (e.g., posted speed limit, lane width, pavement condition, number of lanes, etc.) while the time-variant factors include traffic conditions (i.e., traffic flow and density), vehicle mix, incidents, and driving characteristics [2] [3] . Understanding the effect of these factors on the distribution of traffic speed is necessary for predicting and classifying the congestion levels on a highway.
The main objective of this paper is to provide a quantitative analysis of traffic congestion using mixture characteristics of the traffic speed distribution. In the modeling process, each traffic speed record is assumed to come from a hidden traffic state, which is drawn from a linear relation with traffic occupancy. Therefore, the corresponding impact of the traffic occupancy on the expected travel speed in each state is identified. More specifically, the study uses the Bayesian Dirichlet Process Mixtures of Generalized Linear Models (DPM-GLM) to cluster these states. The Dirichlet process mixture (DPM) classifies the hidden state by categorizing the GLM of each state. In addition, the study uses the Bayesian change-point detection (BCD) model to estimate the possible threshold speed value for each of the states. The threshold value is assumed to separate traffic states into homogeneous groups; thus, this procedure facilitates classification of the traffic condition. The BCD model is estimated using a Bayesian approach, which gives the posterior distribution of the threshold values as well as the uncertainty of estimates. To check the consistency of the estimated cut- points by this approach, the classification error method that minimizes the false positive rate in each state is used to estimate optimal thresholds as well. Both posterior distributions of the model parameters for DPM-GLM and BCD are fitted by the Metropolis-Hastings MCMC sampler. The study uses archived traffic data collected for a year in 2015 on an Interstate 295 corridor located in Jacksonville, Florida.
2. Literature Review
Most of the early analytical studies in modeling the characteristics of speed assume that the distribution follows a single-model distribution [4] [5] . Nevertheless, this model may apply only under homogeneous traffic conditions [6] . Recent empirical studies show that the speed distribution exhibits heterogeneous characteristics. The heterogeneity is attributed to many factors, among which are driver behaviors, vehicle type, to mention but a few. These factors cause the speed distribution to have multiple subpopulations depending on the time window of the analysis. To account for heterogeneity in traffic speed or travel time, a mixture/multi-modal distribution is preferred over the conventional unimodal distribution [1] [7] [8] [9] [10] [11] . In contrast to the single-model distribution, the multi-modal distribution consists of two or more distributions whereby the weighted individual distributions are added to form the multi-model. Apart from offering a better fit, the multi-modal distribution offers several advantages compared to a single-model distribution; one of them is the ability to cluster different states of the distribution simultaneously. Therefore, the multi-modal distribution is more flexible than its counterpart [8] [12] . In addition to flexibility, the model incorporates the uncertainty associated with different traffic conditions (states).
Several studies have applied the multi-modal distribution to characterize different traffic conditions. For instance, the study in [13] used the multi-model to evaluate the congestion level. The study limited the multi-model to two mixture components to classify the speed distribution. The study in [6] concluded that the speed distributions might be more than two, depending on the time of the analysis. Results from [14] identified four states of traffic condition, that is, free-flow condition, congestion onset, congested condition, and congestion dissolve (offset) condition. The free-flow condition consists of the nearly symmetrical shape of the travel time or the speed distribution with low median value. Whereas, the congestion onset and offset conditions are characterized by low median value with left skewed distribution. The congested condition consists of higher median value with the right-skewed distribution.
It is worth mentioning studies, which are more closely related to our study. The study in [15] developed an algorithm to identify congestion while considering the influence of visibility and weather conditions. The study by [15] uses the mixture model to estimate the speed distribution in order to describe the traffic conditions. The mean values of the two regimes, i.e., congested and free-flow conditions were described by a linear relationship with visibility and weather condition. Following a similar approach, the study by [16] estimated the speed distribution considering the instantaneous speed and average historical speed as independent variables to the mean values of the component. Moreover, the study in [12] evaluated the impact of the signal timing on the travel time distribution. The study found that using the multi-modal distribution with varying mixing probabilities improves the model fitting performance. In contrast to standard multi-modal distribution, the varying mixing probability model allows flexibility in following the underlying stochastic process of the data distribution [12] . In addition, the mean values of each mixture components are classified depending on the associated factors.
In all closely related literature aforementioned, the expectation-maximization (EM) approach for estimating the parameters was used. The EM method is susceptible to a local minima problem (over-fitting). In this study, the Markov Chain Monte Carlo (MCMC) approach that treats the model parameters as distributions is used. Apart from eliminating the over-fitting problem, the posterior distribution of the parameters estimated by this method can be updated easily when new data become available. Besides, it incorporates a prior knowledge regarding speed distribution [17] , which adds an advantage on estimating posterior distributions with less number of sample size as compared to EM approach [17] [18] . Additionally, this study incorporates the influence of the traffic occupancy on the multistate speed characteristics, which has not been addressed by the previous studies.
3. Model Framework
3.1. Dirichlet Process Mixtures of Generalized Linear Models
In the commonly used finite mixture models, the expected mean values of the given observations, such as speed in each component mixture are constants. In this study, the conventional method is extended such that it depends on the explanatory variables, . The Dirichlet Process mixtures of Generalized Linear Models (DPM-GLM) (symbols definition in Table 1) can be represented hierarchically as follows [19] :
. The Dirichlet Process mixtures of Generalized Linear Models (DPM-GLM) (symbols definition in Table 1) can be represented hierarchically as follows [19] :
 (1)
(1)
The GLM parameters are linear predictors given by:
![]()
Table 1. Variables/parameters definition for Equation (1) through (4).
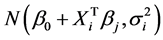 (2)
(2)
 (3)
(3)
The above DPM-GLM is implemented using the stick-breaking process (SBP). The SBP involves breaking a unit length stick into disjoint pieces repeatedly [20] . The initial break,  , is determined randomly with a probability
, is determined randomly with a probability , which is considered as the probability of the first mixture component. After the first break, the next break,
, which is considered as the probability of the first mixture component. After the first break, the next break,  , has the probability
, has the probability . The process of breaking continues until the desired n number of clusters (
. The process of breaking continues until the desired n number of clusters (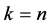 ) are created. On the other hand, when the process of breaking continues until the infinite number of clusters is created the model become nonparametric with infinite mixture states/components [21] . However, the literature point out that working with the infinite dimensional posterior distribution is computationally expensive [22] . By focusing on Equation (3) above, the stick-breaking construction process considers the following conditions:
) are created. On the other hand, when the process of breaking continues until the infinite number of clusters is created the model become nonparametric with infinite mixture states/components [21] . However, the literature point out that working with the infinite dimensional posterior distribution is computationally expensive [22] . By focusing on Equation (3) above, the stick-breaking construction process considers the following conditions:
 (4)
(4)
Estimating the posterior distribution of the hierarchical Bayesian model is analytically challenging as it involves high dimensional integral in the marginal likelihood [7] . To address this problem, the common method for approximating the model parameters is the MCMC simulation. This study considers also MCMC simulation to estimate the posterior distribution of the unknown parameters. In particular, we adopt Metropolis-Hastings sampling step through PyMC3, an open source package [23] . The Metropolis-Hastings sampling step uses the acceptance or rejection rule to draw samples to the proposed posterior distribution [23] . The prior of the distribution is taken as non-informative with Gamma (1, 1) for concentration parameter of the Dirichlet process. Normal (mean = 0, std. = 100) and Uniform (0, 10) for predictor parameter and sigma, respectively. The first 10,000 iterations were discarded as burn-in and following 10,000 iterations were used for inference. To reduce correlations between drawn samples, the sequence of inference iterations was thinned by 10 iterations.
3.2. Model Selection
In this study, three information criteria, which are the Bayesian information criterion (BIC), the Akaike information criterion (AIC), and the Deviance Information Criterion (DIC) were used to select the optimal number of mixture states. All information criteria balance between model complexity (i.e., the number of parameters required) and accuracy in prediction to identify the most appropriate model. The model with the smallest score is selected as the best model among a set of candidates. The BIC is defined as:
 (5)
(5)
The AIC is given as:
 (6)
(6)
where k is the number of estimated parameters, L is the maximized likelihood of the model, and n is the number of observations.
In Bayesian statistics, the DIC is commonly used for the goodness of fit test [24] . Equation (7) defines the model, where  is the posterior mean of the deviance and
is the posterior mean of the deviance and  is the measure of model complexity, estimated by
is the measure of model complexity, estimated by , and
, and  is the deviance evaluated at the posterior means of the parameters [25] .
is the deviance evaluated at the posterior means of the parameters [25] .
 (7)
(7)
3.3. Traffic Speed Change-Point Detection
Similar to clustering task, change-point detection (BCD) represents a threshold value/location that divides data into distinct homogeneous groups. The process of detecting the change-point is well established in time series problem, whereby the main purpose is to identify the shift in trends such that the pattern before and after a threshold value are different [25] . In change-point detection analysis, generally, the number of change-points and their threshold value are unknown. In the literature, several methods exist in establishing a change-point whereby most of them identify this value through means, variances, amplitude or both change in a sequence of observation [25] . Recent studies extended a change- point detection problem to regression models. To illustrated change-point, Figure 1 indicates the regression model with one and two change-points from a simulated data.
In computing the change-point using the Bayesian approach, the assumption about parameter estimation is needed. Herein, we analyzed the problem considering a linear regression with normality assumption. The following model indicates an example of the change-point detection problem with two switch points [25] :
![]() (8)
(8)
where switch point refers to the speed where the pattern changes, a is the speed less than![]() , b represents speeds between
, b represents speeds between ![]() and
and![]() . c represents speeds greater than
. c represents speeds greater than![]() ,
, ![]() is the speed record in the dataset,
is the speed record in the dataset, ![]() is the occupancy coefficient and
is the occupancy coefficient and ![]() is the transpose of covariates,
is the transpose of covariates, ![]() is the standard deviation of the data. min_speed and max_speed is the minimum and maximum speed in the dataset, respectively.
is the standard deviation of the data. min_speed and max_speed is the minimum and maximum speed in the dataset, respectively.
![]() (a)
(a)![]() (b)
(b)
Figure 1. Illustration of a change-point in regression model. (a) One change-point data; (b) Two change-points data.
The above model can be easily modified to infer the change-point in the explanatory variables instead of the response variable. Prior to estimating the model parameters, the number of change-point was inferred from the optimal number of clusters established through information criterion methods (see model selection section). Afterward, the above model parameters are estimated via the Bayesian approach. In particular, we implemented in Pymc3 [23] and Metropolis-Hastings sampling step is selected for the analysis. The prior distribution of the switch points was taken as a uniform distribution with equal probabilities of falling at any traffic speed in the dataset. Before sampling the posterior distribution, the optimization technique through the maximum a posteriori (MAP) was applied to find initial parameters with relatively high probability.
We also considered the classification error method that minimizes the false positive rate in each component to estimate the threshold values [15] . During modeling, the optimal value is estimated by computing a speed that intercepts the two conservative normal distributions (that is, mixture components). Mathematically, this value is found by equating the two normal distributions and then finding the speed value that has the same frequency in the dataset. The purpose of using this method is to compare with BCD estimates.
4. Study Data and Speed Estimation
The study used traffic data from a 4.8-mile corridor of the Interstate 295 freeway (Figure 2) located in Jacksonville, Florida. In the analysis, we consider only southbound traffic in evaluating the proposed model. The corridor runs from Park Ave to San Jose Blvd interchange. The posted speed limit in the corridor is 65 miles per hour (mph).
The archived traffic data for analysis were provided by the Regional Integrated Transportation Information System (RITIS). The dataset is composed of spot speed and traffic occupancy collected from microwave vehicle detectors (MVD) aggregated at 15-minute intervals. The data gathered were collected for the period of January 1, 2015 through December 31, 2015. Weekend, holidays, and days in which incidents (crashes, work zones, etc.) happened were omitted from the dataset to reduce variability. The average speed from the MVD was calculated and considered to represent the link travel speed.
The corridor travel speed was estimated using Equation (9).
![]() (9)
(9)
where n represents the number of detectors on a link (five (5) detectors are used), and ![]() is the spot speed of MVD j at time t.
is the spot speed of MVD j at time t.
Figure 3 summarizes hourly traffic speed in the dataset. The figure shows that
![]()
Figure 3. Summary of hourly speed observations of a corridor.
the morning peak hour occurred between 7 a.m. and 8 a.m. while the evening peaking hour occurred between 5 p.m. and 6 p.m. Closer examination of Figure 3 reveals that traffic frequently experiences lower speeds, particularly during the morning peak hours.
In modeling of the mixture model, the stationary stochastic process is required. However, the speed characteristic is noisy in nature and a long time window of analysis is usually nonstationary. To address the problem, it is a common approach dividing the speed into intervals to create a stationary characteristic and then mixture models are applied to account for heterogeneity in speed data [6] [12] . In this study, three intervals were identified; that is, morning peak hours (Z1) which range between 6 a.m. to 9 a.m., off-peak hours (Z2) from 10 a.m. to 2 p.m. and evening peak hour (Z3) from 3 p.m. to 7 p.m. (Figure 3). In evaluating the traffic congestion, morning and evening peak hours were considered as the time window of the analysis.
5. Results and Discussion
The model selection results based on AIC and BIC criteria are shown in Figure 4. According to this figure, the optimal number of clusters during the morning peak hours is three mixture components while the evening peak hours revealed four traffic states. Since the Bayesian approach is computationally intensive, we used BIC and AIC results as prior to estimate the Deviance Information Criterion (DIC). In the analysis, two, three and four mixture components DIC fit were compared. The results suggest that three components are the optimal number of clusters for both peak hours (Table 2). Comparing the BIC and AIC of the four and three mixture components on the evening peak hours, no significant difference in the fitted value between these models was observed. Consequently, we applied three states in the analysis, which correspond to the free-flow, congestion onset/offset and the congested condition. These states are somewhat similar to the research findings by [14] . In this study, four states are indicated; free-flow, congestion onset, congestion offset and the congested con-
![]() (a)
(a)![]() (b)
(b)
Figure 4. The BIC and AIC score. (a) Morning peak hours; (b) Evening peak hours.
dition. Nonetheless, the distribution characteristics of congestion onset and congestion offset are similar and are considered as one state in our study, i.e., transitional flow condition.
Table 3 gives the posterior mean, standard deviation and Bayesian credible interval (BCI). Based on the BCI, it can be inferred that the estimated coefficients are all significant at the 95% BCI. It is because the effects of the traffic occupancy in each state do not consist of zero values in the BIC [26] . Comparing the influence of traffic occupancy on the speed distribution, model results show that the traffic occupancy affects the congested and free-flow traffic conditions more compared with the congestion onset/offset. To clarify, consider the morning peak hours’ parameters. The free-flow revealed −0.16 as the coefficient and −0.15 for the congested condition, whereas −0.03 is estimated during the onset/
![]()
Table 3. Posterior summary of the model parameters.
Note: BCI is the Bayesian credible interval, Std. stands for the standard deviation of the posterior distribution; MC error represents the Monte Carlo error.
offset condition. A similar pattern was seen during the evening peak hours.
Figure 5 illustrates the drawn samples for the morning peak hours established in the analysis. The drawn samples were obtained by discarding the first 10,000 iterations and using the next 10,000 iterations for inference of the posterior distribution. The inference iterations were thinned by 10 to reduce autocorrelations between samples. As indicated in a figure, left column plots show kernel densities of the marginal posterior distributions of the random variable. Moreover, the graph shows three clusters of traffic speed and occupancy relationship, which are clearly separated from one another. The p, alpha, and beta_1 random variable correspond to the mixture weight, GLM parameters for constant and occupancy respectively. On the other end, sigma represents the variability of occupancy around the mean. In the right column figures, the Markov Chain sampling paths in sequential order are presented. Based on the figures, we may say that the chains are quite stable with respect to variability suggesting that convergence of the random variables was achieved.
The results of mixture components show that the morning peak hours revealed a higher proportion of free-flow speed data (60%) followed by 27% for
![]()
Figure 5. Posterior predicted clusters estimated by 10,000 iterations for the morning peak hours.
congestion onset/offset speed and congested speed being the least (13%). On the other hand, evening peak hours indicated a higher percentage of data in congestion onset/offset (nearly 89%) with the least data in the congested state (0.43%). Comparatively, the morning peak hours experience more congestion than evening peak hours (Figure 6). These findings are also consistent with the summary analysis of the hourly speed distribution presented in Figure 3. In practice, it is indicating that the majority of the traffic travels southbound in the morning and northbound in the evening hours resulting in southbound evening peak hours being less congested.
Figure 7 shows histograms of traffic speed along with predicted posterior density. This figure shows that data, kernel density, and predicted posterior densities are close to one another, suggesting that mixture of the normal distribution can accurately estimate the distribution. Further analysis of the figure, the morning peak hour shows clearly the three clusters of the traffic condition. On the other end, due to low congestion data point on evening peak hours, the three clusters are not clearly visible in Figure 7(b).
Traffic State Cut-Point
To assess the effectiveness of the change-point detection (BCD) approach, the study started with testing the model using simulated data prior to modeling traffic dataset. The results were reasonable given that the estimated parameters were
![]()
Figure 6. Estimated weight of the mixture components.
![]() (a)
(a)![]() (b)
(b)
Figure 7. Posterior predicted clusters with three mixture components. (a) Morning peak hours; (b) Evening peak hours.
close to the actual parameters. Then, the developed model was applied to traffic data to detect the speed threshold values. Figure 8 shows the results of analysis using this approach.
Figure 8 shows 45 miles per hour (mph) and 64 mph are threshold values for congestion and free-flow speed during morning peak hours, respectively. During the evening peak hours of the same traffic direction, the cut points were estimated at 48 mph and 66 mph for congested and free-flow traffic conditions, respectively. To clarify these values how they appear in the speed distribution, Figure 9(a) gives a graphical representation of the cut-point speeds. Based on the results in Figure 9 it can be said that the estimated values are close to the observed separation points of the mixture components of the traffic speed distribution.
![]()
Figure 8. Estimated threshold values of the states.
![]() (a)
(a)![]() (b)
(b)
Figure 9. The cut-point of the traffic states during the morning peak hours. (a) BCD- model results; (b) Misclassification error method-model results.
Using the classification error method, the morning peak hours indicated 47 mph speed for congestion and congestion onset/offset cut-point value while the free-flow condition was estimated to have a speed greater than 64 mph (Figure 9(b)). The model results for the evening peak hour, on the contrary, failed to identify the congested state cut-point speed. This may be due to having a few (only 0.43%) speed records for congested state condition (Figure 7(b)). This might have affected the analysis of cut-point using this method.
Comparing the estimate from the classification error method and BCD method, the threshold values are close to one another with a smaller difference. Moreover, these findings are consistent with findings reported in the literature. For instance, a research conducted by [15] used classification error method to define threshold speed for congestion condition. Although the study considered only two states, i.e., congested and non-congested, the finding for the threshold is estimated at nearly 56 mph, which is close to our model findings.
6. Conclusions
The main objective of this paper was to provide a quantitative analysis of the traffic congestion using mixture characteristics of the traffic speed distribution. In the modeling process, each speed record was assumed to come from the hidden traffic state, which is linearly related to the traffic occupancy. The study used the Bayesian Dirichlet Process Mixtures of Generalized Linear Models (DPM- GLM) to achieve this task. Furthermore, the study used Bayesian change-point detection (BCD) approach to estimate the possible threshold speed value for the established states, which separates the states into homogeneous groups. In addition, the classification error method that minimizes the error in each mixture component was used for the purpose of comparison with BCD results.
To accomplish the study, data collected from the Interstate 295 freeway corridor in Jacksonville, Florida were used. The archived traffic data used in the analysis were collected in the corridor using microwave vehicle detectors (MVD) and were aggregated at a 15-minute interval. The data gathered were collected for the period of January 1, 2015 through December 31, 2015.
According to the information criteria analysis, three traffic states were identified as the optimal number of mixture states that provide a better trade-off between model complexity and accuracy in prediction. These states correspond to free-flow, transitional flow condition (congestion onset/offset), and the congested condition. The results of mixture components indicated that the proportion of congested speed is greater for the morning peak hours (13%) compared with the evening peak hours. Furthermore, congestion onset/offset speed and free-flow speed were estimated with the highest proportion among the components during the evening peak hours and the morning peak hours, respectively. The change-point detection approach demonstrated that it can be used to estimate the cut-point speed in order to classify different traffic states. In the model results, 47 mph and 48 mph are indicated as speed for congestion and congestion onset/offset cut-point value during the morning peak hours and evening peak hours, respectively. The free-flow speed is estimated at the speed greater than 64 mph and 66 mph for morning peak hours and evening peak hours, respectively.
The proposed approach can be used to identify accurately clusters of low-speed regimes to better detect congestions. The approach can be used both in a retrospective analysis of historical data evaluation and prospective evaluation to identify congestions in real-time. Practically, dissemination of this information to the public is very important so that regular and non-regular commuters can make well-informed decisions in order to avoid delays and congestion.
7. Limitations and Recommendations
It is important to note that the data used in this study were aggregated at 15-minute intervals. It is not clear whether similar conclusions can be generalized to other time intervals (such as 5-minute, 1-hour etc.) of data aggregation. Future studies may consider using different time interval in the analysis. Furthermore, this study focused on evaluating the impact of traffic occupancy in characterizing traffic congestion. However, there are other factors that influence traffic conditions; therefore, evaluating the impact of other time-varying factors such as the effect of incidents, vehicle mix, weather, driving characteristics and other factors should be considered in future studies. It is also recommended that this methodology be extended to a longer corridor and large-scale road networks.