Research on the Solution of Cell Invasion Model with Free Boundary ()
1. Introduction
As well known, cancer disease is one of the leading causes of death worldwide. Many natural and man-made factors (for example, smoking, car exhaust fumes, ultraviolet rays, air pollution and radiations, etc.) are the main risks for cancer disease. Metastasis is a leading death process, in which two processes are crucial from the viewpoint of cancer therapy. The first one is angiogenesis, nucleation of new blood vessels, which can provide enough nutrients to further development of tumor cells. The other one is tissue invasion. After the vascular growth of the tumor, cells become more aggressive that it can invade into the extracellular matrix, even into blood vessels, to complete the metastasis. Tissue invasion is a process in which cells can migrate and establish a new colony in new organs.
There are many studies about angiogenesis inhibition, because cancer cells have a certain size and cannot grow further without nutrients from blood vessels. Signaling molecule VEGF (vascular endothelial growth factor) can be secreted by cancer cells and can bind the normal endothelial cells to form new blood vessels. Scientists found inhibitors, such as bevacizumab, to block VEGF [2] . Bevacizumab binds to and disables VEGF to activate endothelial cells to create new blood vessels. This therapy is already applied clinically.
To reduce the ability of invasion is also one way to prevent metastasis. Cancer cells can spread by degrading ECMs. ECMs are degraded by the assembly of the actin cytoskeleton in invadopodia―the invasive feet of cancer cells. In fact, MMPs (matrix metalloproteinase), the family of ECM degrading enzymes [3] , are up-regulated by signals from growth factors [4] . Then, after up-regulation of MMPs, actin assembly delivers it to the invasive site of cancer cells [5] . At the invasive site MT1-MMP (membrane-type MMP), part of MMPs, are responsible to cut laminin-5 [6] . 2 chains of laminin-5 after cleavage can bind to receptor molecules and send signals to drive actin assembly and MMP up-regulation.
Mathematical medicine and biology have become one of the popular topics in the study of modern applied mathematics. Where, cancer cell invasion models have received much attention in recent years [1] [7] [8] [9] [10] [11] . Research [7] has introduced a PDE model to observe the tissue invasion and tumor growth. Then research [8] , based on the discrete-continuum hybrid simulation, promoted the study in [7] by considering the interactions, cell-cell adhesion and other essential functions of cells. There are many other studies relating to the growth of the tumor. For example, in [1] , the authors are aiming to find out numerically how positive feedback affects the formation of invadopodia and invasion of cancer cells. They considered a model for the formation of invadopodia and reaction between proteins, such as act in monomers, ECM (extracellular matrix), signals and MMP (matrix metalloproteinases), which are playing significant role in cancer cell invasion. In the numerical simulation, the authors examined the effects of the molecules by varying the rate constants, and successfully reproduced invadopodia-like small protrusions, which have a similar scale of the real phenomenon, eventually, investigated the leading source of invadopodia; however, they did not study a boundary for cell body, which leads actins diffused into extracellular area.
To the best of our knowledge, studies on the cancer cell invasion model with free boundary are fairly rare. For that reasons, in this paper, we study a modified cancer cell invasion model with free boundary problem. The method used in this paper is motivated by Stefan problem.
In order to obtain cancer cell invasion model with free moving boundary, we need to consider the biological background of the problem. For the reader’s convenience, we will introduce the process of invadopodia formation. Invadopodia are the invasive feet (as shown in Figure 1) of cancer cells which can degrade the surrounding matrix (mainly ECMs), and cause metastasis [12] . Invadopodia are enriched in act in filaments, which are cytoskeletal structures and pushing cell membrane to drive invadopodia.
![]()
Figure 2. Cleavage of laminin 5 by MT1-MMP at juxtamembrane produce laminin-γ2 which can bind to the receptor and can send signals.
ECM fragments are decreased by the reorganization of actin cytoskeleton indirectly [13] . Actins can transport MMPs to the invasive site of cancer cells, top of the invadopodia. MMPs can break and degrade the ECMs, broken ECM fragments in return bind with receptors on the cell membrane, and induce signals to reorganize actins and MMPs. Again, MMPs can break more ECMs, and become a positive feedback loop. We summarize the interactions as shown in Figure 2.
We improved the model considered in [1] by introduce a new variable 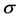 which stands for the signal droved by the connection of ECM fragments and receptors. ECM fragments are created near the membrane by degradation of ECMs. Hence, the corresponding mathematical model is described as follows:
which stands for the signal droved by the connection of ECM fragments and receptors. ECM fragments are created near the membrane by degradation of ECMs. Hence, the corresponding mathematical model is described as follows:
 (1)
(1)
where, 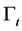 stands for the free moving boundary,
stands for the free moving boundary,  stands for the boundary velocity,
stands for the boundary velocity, 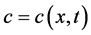 ,
, 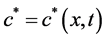 and
and  are stand for the concentration of ECM, ECM fragments and MMPs, respectively. ECM fragments (laminin γ2 chains) bind to cell membrane receptors and send signals to the actin reorganization, where signals have random motility. Hence, we have
are stand for the concentration of ECM, ECM fragments and MMPs, respectively. ECM fragments (laminin γ2 chains) bind to cell membrane receptors and send signals to the actin reorganization, where signals have random motility. Hence, we have
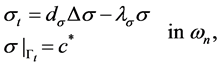 (2)
(2)
where,  represents signal concentration. The first equation of (2) describes the random motility and self decation of signals. The second equation of (2) describes ECM fragments bind to cell membrane and derive signals.
represents signal concentration. The first equation of (2) describes the random motility and self decation of signals. The second equation of (2) describes ECM fragments bind to cell membrane and derive signals.
Free boundary  is defined as
is defined as
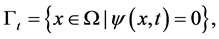 (3)
(3)
where, 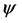 is the level set function, and demands level set equation
is the level set function, and demands level set equation
 (4)
(4)
Since the membrane pushed by the F-actin which is reorganized by signals from cell receptors, therefore, the velocity of the membrane depends on the gradient of signals which cause F-actin polymerization. Hence, boundary velocity defined as follows:
 (5)
(5)
Finally, we derived the modified cancer cell invasion model with cell boundary described as (1-5), our main purpose is to generalize this model into Stefan problem, then analytically discuss its solution.
The organization of this paper is as follows. In section 2 we present some basic definitions, assumptions and related properties, such as characteristic curve of the problem, Greens functions etc., to simplify the problem. In section 3, the main results, related theorem and its proof, of our paper was stated. Finally, the detailed calculation from (48) to (49) and (50) is given in Appendix A, B, C.
2. Preliminaries
The previous section, we stated the biological background and modified cancer cell invasion model with free moving boundary (1 - 5). In this section, we will introduce some basic definitions and related preliminaries, such as Gaussian Kernel, Green function and derivation of Stefan problem etc., which would be useful in proving main results and solutions of Stefan problem (27) in section 3.
2.1. Characteristic Curve
In this paper, for simplicity, we take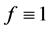 , and discuss the model in 1 dimension. Hence, the level set Equation (4) is rewritten in the following form
, and discuss the model in 1 dimension. Hence, the level set Equation (4) is rewritten in the following form
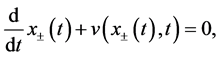 (6)
(6)
where, ![]() stand for the right and left side boundary positions, which depends on time
stand for the right and left side boundary positions, which depends on time![]() ,
, ![]() stand for the velocity of right and left side boundaries (Figure 3).
stand for the velocity of right and left side boundaries (Figure 3).
Take![]() , which satisfies
, which satisfies
![]()
where ![]() satisfies semi-group property:
satisfies semi-group property:
![]() (7)
(7)
![]()
Figure 3. The positions of boundaries at time t.
Consider the following equation of c,
![]()
One can write
![]()
Then we easily have the solution
![]() (8)
(8)
where ![]() is arbitrary constant. We take
is arbitrary constant. We take![]() , then we have
, then we have
![]()
By (8), it follows that
![]() (9)
(9)
By ![]() and (9), we have
and (9), we have
![]()
When ![]()
![]()
Now we take
![]()
and finally we can get
![]()
By using an argument similar to the above, from the equation
![]()
we have the solution
![]()
Then signals ![]() on boundary satisfies
on boundary satisfies
![]()
Finally we have,
![]() (10)
(10)
with
![]() (11)
(11)
The Equation ((10) with (11)) is our key problem for the solution of (1-5). If we can get the solution of sigma from (10) and (11), then we can easily find the solution ![]() from the following equation
from the following equation
![]() (12)
(12)
2.2. Gaussian Kernel
First, consider initial condition problem
![]() (13)
(13)
Now, we multiply ![]() to both sides of (13), and take
to both sides of (13), and take ![]() then we have
then we have
![]() (14)
(14)
If ![]() defined in the whole domain
defined in the whole domain![]() , then the solution of (14) would be
, then the solution of (14) would be
![]() (15)
(15)
where,
![]() (16)
(16)
However, ![]() (or
(or![]() ) is defined in bounded domain
) is defined in bounded domain ![]() therefore we cannot have the solution (15) for our case. But, at least we can see that the Gaussian function
therefore we cannot have the solution (15) for our case. But, at least we can see that the Gaussian function ![]() is differentiable against
is differentiable against ![]() and
and![]() , and satisfies heat equation
, and satisfies heat equation
![]()
Thus, we can say that ![]() is can be a fundamental solution for the heat equation.
is can be a fundamental solution for the heat equation.
Next, consider parameters ![]() in Gaussian function
in Gaussian function![]() . Define a new function
. Define a new function
![]() (17)
(17)
![]() is differentiable for all x and t except
is differentiable for all x and t except ![]() and satisfies
and satisfies
![]() (18)
(18)
If we consider ![]() is the function of
is the function of ![]() with parameters
with parameters![]() , then
, then ![]() is differentiable for all
is differentiable for all ![]() and
and ![]() except
except![]() , and satisfies
, and satisfies
![]() (19)
(19)
Note that
![]() (20)
(20)
![]() is also be a fundamental solution for the heat equation. Next we apply this fundamental solution
is also be a fundamental solution for the heat equation. Next we apply this fundamental solution ![]() to express the solution for the initial value problem (14).
to express the solution for the initial value problem (14).
2.3. Green’s Function
In order to find the solution of (14), we need to introduce new function as follows
![]() (21)
(21)
![]() (22)
(22)
Clearly, we can see that ![]() and
and ![]() are differentiable for all x and t except
are differentiable for all x and t except ![]() and
and ![]() and satisfies
and satisfies
![]() (23)
(23)
and ![]() and
and ![]() are differentiable for all
are differentiable for all ![]() and
and ![]() except
except![]() , therefore satisfies
, therefore satisfies
![]() (24)
(24)
Since,
![]()
by (18), we can easily prove (23) and (24). Using the third property of ![]() in (20), we can get
in (20), we can get
![]() (25)
(25)
![]() (26)
(26)
where, ![]() and
and ![]() are called Green’s first type function and second type function, respectively.
are called Green’s first type function and second type function, respectively.
2.4. Free Moving Boundary Problem
Now, we consider free moving boundary ![]() as in Figure 4 with the following system:
as in Figure 4 with the following system:
![]() (27)
(27)
where,
![]()
Similar to (13), we have the following system
![]() (28)
(28)
where,
![]()
Define a domain D as (Figure 4)
![]()
Take ![]() as,
as,
![]() (29)
(29)
Furthermore, from (24), we know
![]() (30)
(30)
in D. Combining (29) and (30), we have
![]() (31)
(31)
According to Green’s formula, the left side of the Equation (31) becomes
![]()
Finally, we have
![]() (32)
(32)
since,
![]()
When![]() , the left side of (32) equals to
, the left side of (32) equals to
![]() (33)
(33)
3. Main Results
In this section we will state the main results, for convenience we will divide this section into two parts. In the first part, we will give three propositions and one theorem. Where, Proposition 1 and Proposition 2 are useful in proving Proposition 3, and Proposition 3 proves Theorem 1. Theorem 1 represents the solution of ![]() in free boundary problem (27). In the second part, we will derive the solution of boundary velocity
in free boundary problem (27). In the second part, we will derive the solution of boundary velocity ![]() and boundary position
and boundary position ![]() by using condition (12) and Theorem 1.
by using condition (12) and Theorem 1.
3.1. Solution for Free Boundary Problem
In order to prove Theorem 1, we need to prove following three propositions.
Proposition 1. Suppose that, ![]() is continuous for
is continuous for ![]() on
on![]() , when
, when![]() , then
, then
![]() (34)
(34)
holds.
Proof. We consider the left side of (34),
![]()
Since,
![]()
hence,
![]()
This completes the proof of Proposition 1.
Proposition 2. Suppose that, ![]() is continuous for
is continuous for ![]() on
on![]() , when
, when ![]() then
then
![]() (35)
(35)
holds.
Proof. We consider the left side of (35),
![]()
where,
![]()
Since ![]() is small enough, then, we have
is small enough, then, we have
![]()
Next, from the continuity of![]() , for any small
, for any small![]() , there exists
, there exists![]() , for
, for![]() , we have
, we have
![]()
therefore,
![]()
Similarly we can get
![]()
Therefore, (35) follows.
Proposition 3. Suppose that, ![]() is continuous for
is continuous for ![]() on
on ![]() and when
and when![]() , then
, then
![]() (36)
(36)
Proof. From the assumption of Proposition 3, we have
![]()
By Proposition 1 and Proposition 2, we can prove Proposition 3. This completes the proof.
Theorem 1. Suppose that ![]() is continuous for
is continuous for ![]() on
on![]() , then we have
, then we have
![]() (37)
(37)
Proof. Proposition 3 gives the calculation of the first term of form (33). Regarding to the second term of (33), we are using the third property of ![]() in (20),
in (20),
![]()
for![]() . Similarly to (36), we have
. Similarly to (36), we have
![]()
since ![]() not belongs to
not belongs to![]() , therefore,
, therefore, ![]() , and the second term of (33) equivalent to 0.
, and the second term of (33) equivalent to 0.
The above results show that the left side of Equation (32) satisfies
![]() (38)
(38)
Then, we have
![]() (39)
(39)
For the right side of (39), it is clear that point ![]() is separated from
is separated from![]() , and
, and ![]() and
and ![]() is continuous for
is continuous for ![]() on
on![]() , since,
, since,
![]()
and
![]()
Moreover, note ![]() is continuous for all
is continuous for all ![]() and
and ![]() on
on![]() . Hence from the bounded convergence theorem we have
. Hence from the bounded convergence theorem we have
![]() (40)
(40)
for![]() . Now, take together (38) and (40), we have
. Now, take together (38) and (40), we have
![]() (41)
(41)
Equation (41) is useful to prove Theorem 1, which can be written as,
![]() (42)
(42)
This completes the proof of Theorem 1.
3.2. Solution for Velocity
In the above result (37) in Theorem 1, all variables are known except![]() . From the Equation (6) and last condition of (28), we can write
. From the Equation (6) and last condition of (28), we can write
![]() (43)
(43)
![]() (44)
(44)
where, ![]() is velocity of
is velocity of![]() . To define
. To define ![]() we first differentiate the both side of (42), thereupon,
we first differentiate the both side of (42), thereupon,
![]() (45)
(45)
From the definition of ![]() one can easily get
one can easily get
![]() (46)
(46)
then,
![]()
If we use above property, (45) becomes,
![]() (47)
(47)
Next, from (23), we have![]() , thus, (47) becomes
, thus, (47) becomes
![]() (48)
(48)
When ![]() tends to
tends to ![]() from the left,
from the left,
![]() (49)
(49)
(See appendix for specific information).
![]() (50)
(50)
When![]() ,
,
![]() (51)
(51)
Integrate both sides of (43) from 0 to t, we have
![]()
therefore, we have
![]() (52)
(52)
Refer appendix for specific information about how (49) and (51) are followed by (48) as ![]() and
and![]() , respectively.
, respectively.
4. Conclusions
Actin filaments are cytoskeleton in cytoplasm, which can drive cell deformation, migration [14] , and even invasion to the surrounding matrix [15] . How actin filaments are driving cancer cell invasion has been discussed in [1] . They considered four particles, actins, ECMs, MMPs and ECM fragments, where actins and MMPs act in intracellular area, ECMs and ECM fragments exist in extracellular area. Although, they had an excellent result which can describe the deformation of the cell membrane; however, they cannot control the actins, which should not be in extracellular area, diffused throughout the whole domain. To improve the work in [1] , in this paper we added a free-boundary![]() , which is defined as (3), to separate the whole domain into two sub-domains, intracellular domain and extracellular domain. Where, the free-boundary
, which is defined as (3), to separate the whole domain into two sub-domains, intracellular domain and extracellular domain. Where, the free-boundary ![]() is proportional to the cell membrane, which is considered to be pushed by actin assembly (n), and hence we took the boundary velocity
is proportional to the cell membrane, which is considered to be pushed by actin assembly (n), and hence we took the boundary velocity ![]() depending on the assembly rate of actin proteins.
depending on the assembly rate of actin proteins.
Colin et al [16] introduced a model to describe endothelial cells’ migration on bioactive micro-patterned polymers. In their model, the chemotaxis term is considered as cell-cell interaction, therefore, they considered two domains, the adhesive domain and the non-adhesive domain, where adhesive areas are surrounded by non-adhesive areas. By the motivation of the work in [16] , we divided the domain into two parts; however, because of the high complexity of the model, it is difficult to deal with the solution. Thus, we simplified the model and turn the problem into Stefan problem (27), and then consider its solution in one-dimen- sional case. As a result, integral equations ![]() and
and ![]() were obtained. Therefore, problem of solving system (27) was turned to the problem of solving combination of (50), (51) and (52). The results are useful because the system (27) became more suitable to apply finite difference method or other methods, for example, Picard’s successive method. On the other hand, from the biological point of view, the results, in this paper, are not enough to explain the biological meaning; however, they will lead us to further step to discuss the solution of the modified model (1 - 5).
were obtained. Therefore, problem of solving system (27) was turned to the problem of solving combination of (50), (51) and (52). The results are useful because the system (27) became more suitable to apply finite difference method or other methods, for example, Picard’s successive method. On the other hand, from the biological point of view, the results, in this paper, are not enough to explain the biological meaning; however, they will lead us to further step to discuss the solution of the modified model (1 - 5).
We have more interesting topics which deserve further investigations, such as numerical simulations of the integral equations (48, 50 - 52) and how we can get the solution of the original modified model (1 - 4) based on integral solution.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos.11401509) and the Natural Science Foundation of Xinjiang University (Starting Fund for Doctors, Grant No. BS130102).
Conflict of Interests Statements
All authors of this article declare: there is no conflict of interests regarding the publication of this article.
Appendix
This appendix provides specific information about how we get (49) from (48).
a) Confirmation of
![]() (53)
(53)
where, ![]() is continuous in closed interval
is continuous in closed interval![]() .
.
Proof. From the definition of![]() , we have
, we have
![]()
Then, from the definition of![]() ,
,
![]()
where, ![]() is continuous in
is continuous in![]() , therefore, it is clear that
, therefore, it is clear that
![]() is continuous on
is continuous on![]() . Now, we prove there exist
. Now, we prove there exist ![]() such that
such that![]() .
.
For further calculations, we introduce inequality
![]() (54)
(54)
where, ![]() , and
, and ![]() is positive constant. We can prove (54) by
is positive constant. We can prove (54) by
![]() (55)
(55)
then, by the definition of Function-limit, we have for any![]() , and
, and
![]()
then,
![]()
Therefore, applying (54) we can get
![]()
Take![]() , from the continuity of
, from the continuity of ![]() in closed set
in closed set ![]() we can say
we can say ![]() is bounded, and then there exist
is bounded, and then there exist![]() , such that
, such that
![]()
Hence, we have
![]()
which implies that ![]() is integrable for all
is integrable for all ![]()
and continuous for all![]() . Finally applying continuity of integrals theorem, it follows that
. Finally applying continuity of integrals theorem, it follows that
![]()
On the other hand,
![]()
Similarly, we can get
![]()
b) confirmation of
![]() (56)
(56)
Proof. Set
![]()
if ![]() is bounded in
is bounded in![]() , then,
, then,
![]() (57)
(57)
From the definition of![]() , we have
, we have
![]()
Take ![]() is sufficiently close to
is sufficiently close to![]() , and the absolute value of integration on the curve
, and the absolute value of integration on the curve ![]() is
is
![]()
Since, ![]() is sufficiently close to
is sufficiently close to![]() , and the absolute value of
, and the absolute value of ![]() is sufficiently small, hence,
is sufficiently small, hence, ![]() is uniformly converges on any point close to
is uniformly converges on any point close to![]() .
.
Now, prove the continuity of ![]() near
near![]() . Especially, we want to prove that
. Especially, we want to prove that ![]() is continuous on
is continuous on![]() . We prove this using the Definition of Continuity:
. We prove this using the Definition of Continuity: ![]() if
if
![]() (58)
(58)
holds for all![]() . If we can prove there exists
. If we can prove there exists ![]() and (58) holds, then we can prove the continuity of
and (58) holds, then we can prove the continuity of![]() . Now, we divide the integrals,
. Now, we divide the integrals,
![]()
where ![]() is sufficiently close to
is sufficiently close to![]() . (
. (![]() is sufficiently small). Therefore, from the convergence of
is sufficiently small). Therefore, from the convergence of![]() , we can write, for very small
, we can write, for very small![]() , it holds that
, it holds that
![]()
![]()
for all![]() . Furthermore, when
. Furthermore, when ![]() is sufficiently small, then
is sufficiently small, then ![]() is sufficiently small. Next from the continuity of
is sufficiently small. Next from the continuity of![]() ,
,
![]()
Therefore (58) holds, which implies
![]()
c) Conformation of
![]()
where, ![]() is bounded and lipschitz continuous.
is bounded and lipschitz continuous.
Proof. From the definition of![]() , we have
, we have
![]()
where,![]() . For simplicity, set
. For simplicity, set![]() , and
, and
![]()
Suppose,
![]()
hence,
![]()
when![]() , we have
, we have
![]() (59)
(59)
When ![]() and
and![]() , we have
, we have
![]() (60)
(60)
next, from (59) and (60), we can get
![]()
since,
![]()
From the proof of Appendix B, one can know ![]() is continuous near
is continuous near![]() , therefore,
, therefore,
![]()
Finally, we get
![]() (61)
(61)
where,![]() . From Appendix B, we have
. From Appendix B, we have
![]()
Next, we can get
![]()
since, ![]() is away from
is away from ![]() and the integral
and the integral
![]()
is continuous on![]() .
.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ojapps@scirp.org