Evaluation of Maintenance Strategies Based on Leakage Risk Assessment on Side Impervious Walls at Coastal Landfill Sites ()
1. Introduction
Landfill sites where nonrecyclable waste residue is reclaimed are examples of social infrastructure. Large-scale coastal landfill sites are being increasingly constructed in the harbour regions of urban areas in Japan (Figure 1 [1] ) because the limited land availability has increased the costs of inland landfill construction. At both coastal and inland landfill sites, the primary objective is to reduce the environmental risk of the reclaimed waste to the groundwater in the surrounding areas by containing the release of toxic substances. Long-term evaluations in the literature have confirmed that sufficient containment has been obtained [2] . Currently, the selection of coastal landfill sites is mainly influenced by the initial construction cost and the costs of damage caused by the potential leakage of toxic substances due to deterioration of impervious walls [3] . Toxic substances are believed to not leak from coastal landfill sites, and most studies have not included advanced countermeasures as part of maintenance management planning in the event of a leak [3] , mostly because of the lack or nondisclosure of impervious wall monitoring data and the difficulty in predicting impervious wall deterioration. Predicting the deterioration of impervious walls is crucial in the asset management of coastal landfill sites, particularly in the design of their maintenance and the repair strategy. Asset management is a strategic decision-making aspect of social infrastructure that ensures safety by predicting long-term conditions and maximising the convenience under budgetary constraints (Figure 2) [4] .
When establishing the maintenance strategy for a coastal landfill site, the deterioration of a water-sealing is first predicted through high-temperature accelerated deterioration testing of the water-swelling material used in numerous steel side impervious walls. From the results, the amount of toxic substances leaking from site (i.e., total flux) is estimated and used as the decision-making standard. There are uncertainties in the deterioration prediction of impervious walls, and defining toxic leakage is hence difficult. Therefore, risk management- based leakage risk assessment for the total flux is conducted. Risk management is a technique that attempts to suppress to the extent possible the adverse effects of
the risk under budgetary constraints (Figure 3). In this paper, for facilitating the selection of an appropriate repair method, the aforementioned risk management-based concept is applied to the leakage of toxic substances due to deterioration of a steel side impervious wall.
2. Characteristics of Coastal Landfill Sites and Impervious Walls
2.1. Characteristics of Coastal Landfill Sites
Landfill sites can be classified as least-controlled, controlled, and strictly controlled sites, and coastal landfill sites tend to be least-controlled or controlled sites [5] . This study focuses on controlled coastal landfill sites.
Figure 4 depicts a large-scale coastal landfill site in the harbour region of an urban area; it comprises bottom and side impervious walls, collection drainage, a leachate treatment facility, a monitoring facility, and other related facilities (see Figure 4) [3] . Coastal landfill sites have larger areas than do current inland land
![]()
Figure 4. Typical construction at coastal landfill sites.
fill sites. Furthermore, coastal landfill sites entail low risks of contaminating the head of a river.
Because coastal landfill sites face the sea, the difference in water level inside and outside the landfill must be appropriately controlled. In addition, layers of reclaimed waste in such sites can be classified as aquifer and nonaquifer layers, which exist below and above the water level, respectively [2] . Aquifer layers are subject to anaerobic atmosphere, which strongly suppresses the decomposition of toxic substances, prolonging waste stabilisation. Therefore, if the water interception performance of the site deteriorates, even the environment outside the landfill may be contaminated, especially if such deterioration occurs after the landfill site is closed or is no longer monitored. Thus, in addition to monitoring current performance, the prediction of long-term water interception performance is also critical [6] .
2.2. Characteristics and Classification of Side Impervious Walls
Coastal landfill sites must be robust to external factors [5] . Moreover, substances within the landfill, such as the retained water containing toxic substances, must not leak out of the landfill. Further, the impervious walls must seal the sides and bottom of the landfill site to prevent leaching, such as that of contaminated waters (Figure 4), in order to prevent the contamination of the surrounding sea area. This containment performance is strongly influenced by the performance of the impervious walls, which makes the monitoring of these walls essential.
A steel-pipe sheet pile is often used as a side impervious wall. Such a wall is installed as continuous jointed sections (Figure 5). Water leakage through the wall is due to the joints; in other words, the water interception performance of the steel side impervious wall strongly depends on that of the joint section. Therefore, countermeasures (treatments) must be applied to improve the water interception performance so that the joints can satisfy the technical requirements. Various joint shapes and water-swelling materials―sheets or liquid-type high-flowability materials composed of a super absorbent polymer, a filler, and a solvent―have been used for water interception treatment [3] . Water extracted from the swollen membranes satisfies the groundwater quality standards of the
![]()
Figure 5. Joints of steel side impervious walls.
specified toxic substances. When such materials are applied to the joints of the steel-pipe sheet piles, the solvent volatilises, leaving behind an elastic hard film. This film is impervious and thus improves the water interception performance of the joints. In this study, the water-swelling material used as the water interception treatment material is investigated.
3. Estimation Leakage Due to Deterioration of Side Impervious Walls
3.1. Deterioration Prediction for Steel Side Impervious Walls
Deterioration in the water interception performance of steel side impervious walls is believed to be due to the deterioration of the water-swelling material in the joints. In this study, temperature variation is assumed to be the main factor influencing the deterioration of the impervious wall. Other factors include reduction in durability due to chemical reactions and wet-dry cycles. Water- swelling materials do not react with chemical substances except trichloroethylene, dichloromethane, and carbon tetrachloride [7] . Nevertheless, the durability of the water-swelling materials is independent of reactions with these three chemicals in the concentration equivalent with the standard of waste acceptability [3] . Furthermore, the durability of such materials is independent of the swelling ratio and the tensile strength in dry-wet testing. Therefore, temperature variation is the factor that most strongly influences wall deterioration.
Water-swelling materials are expected to possess long functional lifetimes [7] , [8] . Therefore, in this study, high-temperature accelerated deterioration testing was performed, and the deterioration curve of the water-swelling material was plotted from the results of Arrhenius law-based durability evaluation.
3.2. High-Temperature Accelerated Deterioration Testing
Strength is assumed to strongly influence water interception performance because swollen membrane strength and hydraulic conductivity have been previously associated. Specifically, strength decreases as the super absorbent polymer in the water-swelling material dissolves [7] ; this dissolution is inhibited by ions in seawater. Hence, the water-swelling material deteriorates more rapidly in freshwater than in seawater. Therefore, the material was tested in fresh water.
In the high-temperature accelerated deterioration test, the water-swelling material was immersed in high-temperature water, following which the strength of the swollen membrane was measured using an EZTest-500N (Shimadzu Corporation) with an elasticity jig of Φ3 mm, as described herein:
1) 80 mm × 80 mm × 2 mm specimens of the water-swelling material were prepared.
2) The specimens were immersed in a freshwater tank at water temperatures of 20˚C, 40˚C, 60˚C, and 80˚C.
3) The prepared specimens were placed between the upper part of the testing equipment and the lower acrylic plate, both of which are fixed to the equipment by using bolts.
4) The specimens were accelerated as indicated in Figure 6.
5) The specimens were removed from the water tank after predetermined periods of time (from 1 day to at most 43 days), and the strength of the swollen membrane at positions (stations) 15 and 30 mm from the centre of the specimens were measured at nine points in total (Figure 7).
6) The specimens were returned to the water tank.
7) Steps 5) and 6) were repeated.
The relationship between swollen membrane strength and number of days immersed is illustrated in Figure 8. The film strength of the water-swelling material before immersion (swelling) was 6.9 N. Swollen membrane strength decreased with immersion for all water temperatures and stations. In addition, compared with the swollen membrane strength at the central station (No. 1), those at stations 15 mm from the centre (No. 2 and 3) as well as at stations 30 mm from the centre station (No. 6 and 7) decreased independent of the water temperature. The deterioration proceeds from the outer stations to the core because of the contact between the water and the water-swelling material at the surface of the material, which in turn triggers the dissolution of the super-absorbent polymer from the surface. Consequently, the decrease in swollen membrane strength progresses from the surface to the core of the material. However, water cannot easily infiltrate to the core because of the initial swelling
![]()
Figure 6. High-temperatures accelerated deterioration test specimen.
![]()
Figure 7. Measured swollen membrane strength points of water-swelling materials.
around the outer stations of the water-swelling material. The decrease in swollen membrane strength at each station increased with the increase in water temperature. Thus, deterioration of the water-swelling material is higher at higher water temperatures. In a previous study, water-swelling material immersed in
![]()
Figure 8. Relationship between swollen membrane strength and immersion duration. (a) Immersion water temperature: 20˚C; (b) Immersion water temperature: 40˚C; (c) Immersion water temperature: 60˚C; (d) Immersion water temperature: 80˚C.
water at 20˚C for 10 years was reported to exhibit constant strength and water interception performance (i.e., swollen membrane strength of 0.8 N and hydraulic conductivity of 1.0 × 10−9 cm/s) [7] . The super-absorbent polymer thus clearly dissolves within approximately 1 year. In this study, swollen membrane strength decreased and hydraulic conductivity increased with dissolution of the polymer (Figure 8). At 20˚C, swollen membrane strength was maintained constant at approximately 1 N, as dissolution of the polymer did not progress over time at this temperature. From this figure, long-term swollen membrane strength and hydraulic conductivity can be predicted. In addition, the results evidence that immersion water temperature strongly influences deterioration of the water-swelling material.
3.3. Deterioration Prediction of Impervious Walls by Using Arrhenius Law
The Arrhenius law is a physical deterioration prediction model in which the temperature is the main deterioration factor. In this model, the deterioration-induced reaction ratio can be expressed as Equation (1) and is inversely proportional to absolute temperature. Equation (1) is based on the reaction ratio kinetics that a reaction advances early at high temperatures [9] . Therefore, this model is generally used to predict the long-term durability of weak materials, such as polymeric materials, as a function of temperature [10] .
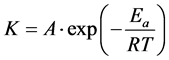 (1)
(1)
where K is the reaction rate, A a constant (frequency factor), Ea the apparent activation energy, R the gas constant, and T the absolute temperature.
Given the reciprocal relationship between reaction rate and service life, expected service life (L) can be calculated using Equation (2).
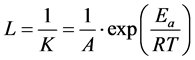 (2)
(2)
On taking the natural logarithm of both sides of Equation (2), we obtai
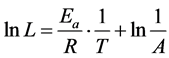 (3)
(3)
where Ea/R and 1/A are constants. Because of the linear nature of this relationship, the reciprocal of the temperature and expected service life can be presumed to be and 1/T and ln L, respectively, meaning that the expected service life at room temperature (20˚C) can be predicted. The Arrhenius law yields the expected service life at room temperature; hence, performance deterioration up to end of the expected service life must be considered.
The durability of the water-swelling material is evaluated using experimental results and the Arrhenius law. However, because data acquisition of the frequency factor (A) is difficult and because apparent activation energy (Ea) is specific to the material, the expected service life―the period over which the material can maintain its initial water interception performance―cannot be calculated using Equation (2). Therefore, the time point at which the assumed ability of the water-swelling material is no longer evident is designated as the end of the expected service life. In this study, the time point at which the swollen membrane strength becomes less than 0.8 N is assumed to be end of the expected service life, because a swollen membrane strength of 0.8 N can support a hydraulic conductivity of 1.0 × 10−9 cm/s under an applied pressure of 0.5 MPa [11] [12] , [13] .
The approximated straight line plotted using Equation (3) shows the relationship between the reciprocal of expected service life (natural logarithm) and the temperature. The service life of the water-swelling materials at room temperature (20˚C) is interpolated from the results of accelerated deterioration testing at high temperatures (40˚C, 60˚C, and 80˚C) by plotting the results obtained at high temperatures in the 1/T-ln L plane. Figure 9 presents the approximated straight line generated using the results of accelerated deterioration testing at 40˚C, 60˚C, and 80˚C; these results support the aforementioned end-of-service- life assumption. Table 1 lists the averages and standard deviations of the inclination (Ea/R) and section (ln 1/A) of the approximated straight line, obtained from the time characteristic of swollen membrane strength at the central station of the specimens.
Because the A and Ea of the material are constant, the slopes of approximated straight lines for the different temperatures should be approximately equal;
![]()
Figure 9. Approximated straight line illustrating the relationship between reciprocal of expected service life (ln L) and temperature (1/T).
![]()
Table 1. Average and standard deviation of inclination (Ea/R) and section (ln 1/A) for the approximated straight line.
however, the results vary considerably (Table 1). One reason for this discrepancy is the measurement error in these tests. In addition, the water-swelling material does not deteriorate uniformly over time. Therefore, the expected service life of the water-swelling material was calculated using the average and standard deviation of the inclination (Ea/R) and section (ln (1/A)) (Table 2) and was found to be approximately 22 years, which is shorter than that reported in a previous study [14] . The water-swelling material in [14] was reported to not undergo further deterioration after immersion for 1 year. Thus, an expected service life of 100 years can be realised by changing the composition of the water-swelling material. However, the service life of the water-swelling material when used in the impervious wall of a coastal landfill site was reported to be on the order of several decades.
In this study, the deterioration in water interception performance due to deterioration of the water-swelling material over its expected service life is examined by adopting hydraulic conductivity as an index of water interception performance. Previous studies [7] [11] [12] [13] investigating the relationship between swollen membrane strength and hydraulic conductivity for the water-swelling material of a steel side impervious wall have reported an initial swollen membrane strength of 7.2 N and a maximum hydraulic conductivity of 8.0 × 10−9 cm/s; these values tend to be stable over the long term, decreasing to 0.8 N and 1.0 × 10−6 cm/s after 1 year, respectively. Therefore, a similar trend is expected for service life, because as the super-absorbent polymer dissolves over time, the density of the material decreases and hydraulic conductivity increases. Figure 10 depicts the deterioration prediction curves, under the assumption that the steel side impervious wall progressively deteriorates every year, obtained when the relationship between service life (natural logarithm) and hydraulic conductivity
![]()
Figure 10. Deterioration prediction curves for steel side impervious wall.
![]()
Table 2. Expected service life of water-swelling materials.
of the water-swelling material is represented as an approximated straight line for the expected service life listed in Table 2. The curves for μ − σ, μ, and μ + σ represent the worst-case, base, and best-case scenarios, respectively. However, numerous deterioration factors influence each other, thereby increasing the complexity of the deterioration mechanism. Because the prediction curves are generated solely by using data from high-temperature accelerated deterioration testing, the predictions must be verified by monitoring the actual deterioration.
3.4. Prediction of Leakage Considering Deterioration in Side Impervious Walls
In coastal landfill sites, leakage of the retained water, which may contain toxic contaminants, occurs through infiltration, advection, and dispersion. These distinct phenomena must be accurately reflected in the estimation of the behaviour of the retained water at the side and bottom impervious walls. In addition, unlike inland landfill sites, the influence of external conditions such as tide must be accounted for in coastal landfill sites. Moreover, because impervious walls in coastal sites are complex structures composed of clays, sands, and steels, the characteristics of these constituents must be considered. Therefore, the deterioration prediction curved line (Figure 10) of a 47 m × 20 m × 5 m steel side impervious wall (Figure 11) is used in the infiltration and advection-dispersion analysis in this study. Specifically, the result (output) obtained one year after the hydraulic conductivity of t is designated as the hydraulic conductivity of t + 1. The three-dimensional cross-section of a steel-side double impervious wall presented in Figure 11 is adopted as the analysis model. This model comprises two impervious walls and filler sand [11] . The constituent layers surrounding the coastal landfill site, namely the sea area, the waste layer, and the natural deposited clay layer, are reflected in the model. The natural deposited clay layer is assumed to accumulate below the waste layer and the sea area, forming the bottom
![]()
Figure 11. Structural model of steel side double impervious wall used in infiltration and advection-dispersion analysis.
layer of the landfill site. Moreover, the Euler-Lagrange finite element method, which combines Eulerian and Lagrangian methods and yields stable solutions for advection and dispersion, is used as the analysis code. Dtrans-3D・EL is used to visualise the unsaturated flow and advection-dispersion behaviours of groundwater and solutions.
The parameters of each constituent layer set are listed in Table 3. The analysis conditions are as follows:
1) The steel side impervious wall is assumed to be a uniform layer, whose hydraulic conductivity is equivalent to that of the water-swelling material and the steel [15] .
2) The penetration depth of the wall is assumed to be 3 m.
3) The parameters of the wall and the bottom layer (natural deposited clay layer) vary in each analysis.
4) The retardation factor (R) shows the adsorption ability of toxic substances and it is assumed to be 2 in the bottom layer [5] [11] [15] .
5) No clear data is available for the molecular diffusion coefficient in coastal landfill sites. Hence, on the basis of three-dimensional infiltration and advection-dispersion leakage analysis of toxic substances in coastal landfill sites reported in [5] , [11] , and [15] , the molecular diffusion coefficient was assumed to be 1.0 × 10−5 cm2/s in all constituent layers.
6) Waste stabilisation is a long-term process, and the analysis period is therefore assumed to be 30 years; the landfill site is utilised after the landfill is closed or abandoned.
7) The difference in water level inside and outside the landfill site would not exceed 200 cm.
8) Infiltration and advection-dispersion parameters used in related studies [11] , [12] [15] are referred to.
Mass flux (mass per unit time and unit area) is the mass of toxic substances that passes through a certain section and is an index frequently used in charac-
![]()
Table 3. Parameters of each constituent layer.
terising the movement of toxic substances [12] . In the evaluation of the environmental safety of landfill sites, the concentration of toxic substances in the water outside the landfill site is routinely monitored. However, even at low concentrations of toxic substances, severe contamination (damage) can occur if the mass flux and flow rate are high. Moreover, at high concentrations of toxic substances, mass flux can be high even at low flow rates. Thus, the mass flux of toxic leakage from the coastal landfill sites must be considered in the evaluation of the environmental safety of landfills.
Mass flux has three components: advection, diffusion, and dispersion flux [13] :
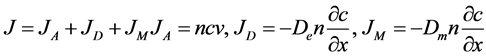 (4)
(4)
where J is the mass flux, JA the flux related to advection, JD the flux related to diffusion, JM the flux related to dispersion, n the effective porosity, c the concentration, v the flow rate in the void, De the effective diffusion coefficient, and Dm the dispersion coefficient.
In this analysis, the total leakage volume (i.e., the total flux) from the steel side impervious wall and the bottom layer is calculated to evaluate the mass of toxic substances that leaks to the sea. The unit of total flux is [cm3] because this yields the dimensionless quantity of 1 for the concentration of toxic substances. Thus, the mass of the toxic substances can be determined by multiplying their concentration [mg/cm3] and total flux [cm3]. However, the concentration of toxic substances cannot be easily determined; therefore, total flux is used. Mass flux is the mass per unit area and unit time, whereas total flux indicates the total amount of toxic substances over the total outflow area and time [13] .
Figure 12 illustrates the relationship between total flux and concentration (C) obtained using the aforementioned method. The total flux increases at C = 0.5 and increases rapidly as C approaches 0.8. Moreover, the figure clarifies that the total flux-concentration relationship is independent of the deterioration curve of the steel side impervious wall. Therefore, total flux can be accurately predicted by monitoring the concentration of the leaking toxic substances. The present analysis is based on the results of high-temperature accelerated deterioration testing, which may deviate from the actual concentration of leaking toxic substances. Hence, the uncertainty of the data used in risk assessment must be represented statistically by using probability density distribution functions.
4. Assessment of Water Leakage Risk in Coastal Landfill Sites
4.1. Risk Factors in Coastal Landfill Sites
A risk generally refers to an event that is undesirable, an occurrence of loss, or a clarification and is defined by a field and a target [13] . The loss may occur in the future and may deviate from that predicted, but the risk must be represented adequately. In this study, the definition of risk used in reliability engineering is adopted, where risk is expressed in terms of the danger posed by an external force as well as its level of damage. Therefore, for any phenomenon, the risk (i.e.,
![]()
Figure 12. Relationship between total flux and concentration.
loss expectation value) can be defined as Equation (5) by multiplying the probability of the phenomenon and the loss level [13] .
![]() (5)
(5)
where R is the loss expectation value, Pi the probability of and Ci the loss due to phenomenon i, and J the total predicted loss.
In this study, the risk management was applied to reduce the risk in coastal landfill sites for the flow indicated in Figure 3. Risk assessment is the quantitative evaluation of the risk factors extracted through risk identification and classification. The most concerning risk in landfill sites is the risk of damage to the surrounding environment (hereafter, environmental risk). Generally, environmental risk can be classified as risk to the human body and risk to the ecosystem [14] . The environmental risk of landfills cannot be zero even if technical specifications and maintenance standards of impervious walls are adhered to and if the waste is treated appropriately [16] . Therefore, each risk factor must be recognised and appropriately responded to. The risk factor that the neighbourhood is regarded as anxiety in the landfill site is detailed as follows, based on the process of waste disposal [17] .
1) Acceptance of waste: When the landfill site accepts waste, there exists a risk of the mixture of different materials.
2) Reclamation of waste: The risk of wastewater seepage is present even long after waste reclamation is complete. This environmental risk is one of the most damaging in landfill sites.
3) Maintenance of landfill site: Maintenance-related risks develop after the landfill site is closed or when the landfill site is no longer monitored (e.g., because of bankruptcy) risk is generated; this environmental risk is distinct from that of a natural environment.
In this study, the environmental risk pertaining to the leakage of retained water in coastal landfill sites (hereafter, leakage risk) is considered the most serious risk. This risk is controlled by constructing impervious walls. However, complete seepage prevention is technically difficult, which highlights the importance of reducing or managing leakage risk.
4.2. Leakage Risk Assessment in Coastal Landfill Sites
A quantitative understanding of the environmental risk is vital in the risk management of coastal landfill sites. Generally, the use value of risk management is high because the risks are easily accepted by all stakeholders when expressed in terms of monetary loss [17] . The primary and secondary objectives of risk evaluation are to quantify the risk and to quantitatively evaluate the effect of countermeasures, respectively. Using judgment indexes, risk management minimises risk-induced losses, for which quantitatively calculating the leakage risk is crucial. However, no techniques have been established for quantifying the environmental risk of landfill sites. Hence, this study employs the loss function and fragility curve used in earthquake risk analysis to quantify the leakage risk in coastal landfill sites [18] .
4.3. Fragility Function
The fragility function is defined as the conditional probability of occurrence on a specified suffering scale. In earthquake risk analysis, this function is usually expressed as a probability density distribution of the damage probability, with earthquake magnitude on the horizontal axis and structural damage on the vertical axis. The probability of occurrence of the suffering scale corresponding to the magnitude of the seismic ground motion can be predicted by setting the limit state displacement to which the response displacement and structural damage caused by seismic ground motion occur as a probability density distribution.
In this study, the concentration and total flux of the toxic substances that leak into the sea area are used as indexes of leakage risk in coastal landfill sites. The probability of exceeding the limit reference set in these indexes is defined as a performance function (X) and a standard exceedance probability (FX) (Equations (6) and (7), respectively).
![]() (6)
(6)
![]() (7)
(7)
where X is the performance function, Ct the concentration or total flux of the toxic substances that leak into the sea area after t years, CA the limit reference setting for each index, and FX the standard exceedance probability. Because of nonnegative conditions, Ct and CA are expressed as lognormal distribution functions.
FX is the concentration of the leaking toxic substances calculated as a probability beyond the closure and abandonment of coastal landfill sites; it is assumed to be C = 0.1 in the present analysis.
Therefore, because the lognormal distribution function is set to the probability density distribution, FX is expressed as Equation (8). FX exceeds the specified limit reference value when uses t years of use passes is calculated. A similar calculation is repeated for an evaluation period of 30 years, and FX for the age of service and index is determined.
![]() (8)
(8)
The average (λX) and standard deviation (ζX) of the performance function (X) can be led such by the median value and coefficient of variation of Ct and CA in Equations (9) and (10). These two parameters determine the sketch of the standard exceedance probability (FX).
![]() (9)
(9)
![]() (10)
(10)
where μCA is the median value in the limit reference set of each index, μCt the median value in the concentration or total flux of toxic substances leaking into sea area after t years of use, υCA the variation coefficient of the limit reference set of each index, and υCt the variation coefficient of the concentration or total flux of toxic substances leaking into the sea after t years.
4.4. Loss Function
The loss function Equation (11) is a function that yields the expected loss (R) corresponding to the damage level and the standard deviation of the expected loss [18] . To use this function, the amount of damage loss (Ci) at the damage level and the occurrence probability (Pi) of the damage level must be known.
![]() (11)
(11)
where Pi is the probability that phenomenon i occurs, Ci the damage loss due to phenomenon i, and J the total number of phenomena.
In this study, the total flux of the leaking toxic substances is used as an index of the damage level of coastal landfill sites. In earthquake risk analysis, the suffering level of a structure is used for predicting the maximum response displacement of an earthquake and the judgment index of the repair method [19] .
The occurrence probability of damage level k (Prob (k)) based on the total flux in the toxic substances that leak from any coastal landfill site can be calculated using the standard exceedance probability (Equations (6) and (7)). This probability must be expressed as a monetary value to facilitate comparison of risks; in this study, this conversion is performed using an endpoint modelling-based lifecycle impact assessment method [20] , developed during 1998-2003 at the Life Cycle Assessment Research Center, National Institute of Advanced Industrial Science and Technology, Japan. Because monetary value (in yen) is used as a joint analysis-based unified index, environmental impact can be allocated a base cost according to the total flux of the toxic substances:
![]() (12)
(12)
where Ek is the damage cost related to the total flux of the toxic substances at damage level k, Jk the total flux of toxic substances at damage level k, ei the coefficient converted into a monetary value, and i the type of toxic substance.
Because the leakage of the toxic substances to the sea area in a coastal landfill site is investigated in this study, the coefficient is converted into a monetary value of discharge into unit area of the sea. Moreover, the damage coefficient accounts for damage to both the ecosystem and the human body. The expected loss value (NEL) relating to toxic substances in coastal landfill sites is
![]() (13)
(13)
where Prob (k) is the damage occurrence probability at damage level k and Ek the damage cost related to the total flux of the toxic substances at damage level k.
The leakage risk of toxic substances considering uncertainties in the degradation of impervious walls in coastal landfill sites is estimated using the aforementioned risk assessment approach.
4.5. Leakage Risk Assessment in Coastal Landfill Sites
For evaluation the leakage risk of toxic substances in coastal landfill sites due to deterioration of impervious walls, the probability density distribution of each index is calculated. In addition, the standard exceedance probability and loss function are calculated for the worst-case, base, and best-case scenarios (Figure 10). The probability density distribution must ideally be determined using numerous samples and check data as well as through simulations such as Monte Carlo simulation; however, in this study, risk assessment is conducted using only three data cases to ensure a reasonable analysis time.
When the concentration of the toxic substances C that leak into the sea area is used as an index, C = 0.1 is set as the limit reference, and when the total flux of toxic substances that leaks into the sea area is used as an index, the limit reference is set at each damage level as listed in Table 4. The limit reference for the total flux after closure or abandonment of coastal landfill sites is set as the value obtained using the flow rate corresponding to C = 0.1, which in turn corresponds to toxic seepage at a hydraulic conductivity of 1.0 × 10−6 cm/s (the value specified in the technical requirements for impervious walls [3] ). Moreover, the limit reference based on these technical requirements is set from the total flux for a hydraulic conductivity of 1.0 × 10−6 cm/s for the side impervious wall and 1.0 × 10−5 cm/s for the clay layer. The probability density distribution is not set because the environmental quality standard value after the closure and abandonment of coastal landfill sites is appropriate as the limit reference (CA) set in the aforementioned case. That is, the damage level corresponding to the total flux of the leaking toxic substances is set as shown in Table 4. The index used to calculate the loss function adopts the total flux of the toxic substances that leak into the sea area to calculate the damage cost, and the expected loss value is calculated using the probability of occurrence of each damage as expressed by its standard exceedance probability.
With these assumptions, risk management can be applied to reduce leakage risk in the coastal landfill site, and the influence of each analytical condition on leakage risk can be quantitatively understood.
![]()
Table 4. Assumed damage level for each level of total flux.
4.6. Results of Leakage Risk Assessment
The leakage risks for different forms of steel side double impervious wall in a coastal landfill site with an internal and external water level difference of 200 cm is presented in Figure 13. Figure 14 and Figure 15 show the standard exceedance probability by concentration and by total flux, respectively, for each form of the wall. The standard exceedance probability by concentration rapidly increases after 13 years for a steel side double impervious wall (Figure 14). For such enrapture as landfills, a standard exceedance probability of 10% after 50 years is considered acceptable [21] . This is equivalent to 475 years if shown at the reproduction period. And the standard exceedance probability after 1 year is 0.2105%, whereas that for a steel side double impervious wall after 12 years is 0.04%, which exceeds the aforementioned threshold. In addition, in the total flux index (Figure 15), for the total flux caused by the closure and abandonment of the coastal landfill site (rank 3), the standard exceedance probability exceeds 10% after 50 years, which is equivalent to that after 15 years for a steel side double impervious wall. Thus, it is difficult to determine whether a steel side double impervious wall can satisfactorily contain toxic substances in coastal landfill sites. Further, these results highlight the necessity of considering the leakage risk of toxic substances at the structural design stage.
Generally, lognormal distribution is adopted in the risk assessment of nonnegative conditions. Moreover, because C = 1.0 - 0.0 is the relative concentration used in this study, the beta distribution that can set the upper and lower bounds is applicable. For the relative concentration of toxic substances leaking from the coastal landfill site targeted in this study, the aforementioned probability density distribution of two patterns is applied in the risk assessment because the compatibility of the probability density distributions was unclear. Figure 16 presents the results of calculations obtained using a standard exceedance probability that uses the lognormal distribution and the beta distribution for the relative concentration of leaking toxic substances. The tendency for a standard exceedance probability differs by established probability density distributions. Although the standard exceedance probability when using the beta distribution increases after
![]()
Figure 13. Internal and external water level difference of 200 cm at a coastal landfill site.
![]()
Figure 14. Standard exceedance probability by concentration.
![]()
Figure 15. Standard exceedance probability by total flux.
![]()
Figure 16. Standard exceedance probability obtained using lognormal distribution and beta distribution.
15 years, that when using the lognormal distribution increases after an equivalent lapse. In other words, as the deterioration of an impervious wall progresses, the results (i.e., standard exceedance probability obtained using the lognormal distribution and that obtained using beta distribution) becomes increasingly conservative. This conservative approach ensures safety by adopting stricter evaluation criteria for the risk assessment of high-risk infrastructure such as nuclear power plants. Because the primary objective of this study is to reduce and manage leakage of toxic substances in coastal landfills, the conservative lognormal distribution is adopted. Nevertheless, the most appropriate probability density distribution must be determined through continuous monitoring of the concentration of toxic substances leaking from coastal landfill sites.
5. Determining Optimal Maintenance Strategies through Leakage Risk Assessment
5.1. Outline
In a coastal landfill site, the leakage risk of toxic substances increases as side impervious wall deterioration progresses. Therefore, appropriate maintenance and repair must be performed to contain the toxic substances until the end of the wall’s intended life cycle. Although appropriate repair methods have been implemented in landfill sites (Figure 17) [22] , no such repair methods have yet been established for coastal landfill sites [3] . The most typical repair method adopted in inland landfill sites with the problem of waste removal causing environmental risk. Examples of other methods include countermeasures for recovering surrounding environments such as leachate treatment and protecting the contaminated water source and soil. Moreover, to prevent further environment damage, new impervious walls can be constructed. Removal of reclaimed waste is another typical countermeasure in inland landfills. Coastal landfill sites generate a large amount of waste than do inland landfills; therefore, countermeasures such as reclaimed-waste removal are unsuitable because of the retained water. In-situ containment by controlling the internal and external water-level difference, repair of impervious walls, and in-situ extraction through leachate treatment are suitable for coastal landfills.
![]()
Figure 17. Repairing methods in inland landfill sites.
When designing the maintenance strategy of social infrastructure, an appropriate repair method and time must be determined for appropriate asset management. Moreover, whether repairing is necessary must be determined through life-cycle cost (LCC) and cost-benefit analyses. Irrespective of the cost, repair becomes essential if environmental risk is demonstrated. In this study, deterioration of the side impervious wall is assumed to be the primary a factor that increases the environmental risk in coastal landfill sites, and repairing the side impervious wall is proposed as a countermeasure, with the leakage risk of toxic substances is adopted as a decision-making index. That is, an appropriate maintenance strategy that considers the decrease in the leakage risk according to the repair method is examined.
5.2. Assumptions
Social infrastructure maintenance strategy must consider such factors as checking intervals, performance level of the infrastructure repair (target level), and the adopted repair countermeasure [23] . Because monitoring is obligatory in landfill sites, checking intervals have not been examined. An appropriate repair method should be determined considering such parameters as budgetary restrictions, the target repair level, and post-repair benefits. In the present analysis, the water interception performance of the impervious wall and leakage of toxic substances into the sea area must be accounted for and used as a repair judgment index, and the toxic leakage risk according to deterioration in the impervious wall is adopted as the decision-making standard. The associated judgment index and the repair method are examined in this section. However, no appropriate methods have yet been established for the repair of side impervious wall, as stated earlier, because of the difficultly of such repair. Therefore, the preferred approach is to recover the hydraulic conductivity of the joint section; hence, reinjection of the water-swelling material is adopted as the repair method.
The following assumptions are made in this analysis:
1) The cross-section of a steel side double impervious wall is used as the analysis model.
2) The evaluation period is 30 years.
3) The internal and external water-level difference in the landfill is 200 cm, and the relationship between the concentration distribution and total flux of the leaking toxic substances obtained in the preceding chapter is used.
4) The concentration, total flux of the toxic substances leaks, and the hydraulic conductivity of the side impervious wall are adopted as the judgment index for repair.
5) Strategies for repairing only the sea-facing steel side impervious walls and for repairing both the seaside and landfill site-side walls are proposed. Moreover, the steel side impervious wall is repaired only once.
6) The hydraulic conductivity of the steel side impervious wall after repair is assumed to have recovered to the initial level (Figure 18). The deterioration curve of the steel side impervious wall after repair adopts the curve of the best-case scenario where deterioration progresses the least.
7) The maintenance strategy sets six patterns (Table 5) by setting the defining point as the time to repair that exceeds the standard in each judgment index.
![]()
Figure 18. Post-repair hydraulic conductivity of steel side impervious wall.
![]()
Table 5. Assumed maintenance strategies at the defining time point (i.e., the repair time at which the standard in each judgment index is exceeded).
5.3. Risk Assessment-Based Examination of Appropriate Maintenance Strategy
In the case where a repair method is not applied, the result indicating the relationship between the concentration and total flux is assumed to be the “base plan”, and the time when the established standard is exceeded in each judgment index in this plan is shown in Table 6. The time when the established standard is exceeded becomes early in order of concentration, total flux, and hydraulic conductivity. In each repair method, the side impervious wall is repaired at the elapsed time listed in Table 6.
In each repair plan, the transition of the standard exceedance probability for a given concentration of toxic leakage is presented in Figure 19. The effect of the
![]() (a)
(a)![]() (b)
(b)
Figure 19. Standard exceedance probability by concentration of leaking toxic substances. (a) Repairing the steel side impervious wall on sea-side only; (b) Repairing the steel side impervious walls on the both sides (sea side and landfill site side).
![]()
Table 6. Time point when the established standard is exceeded in each judgment index.
repair is not confirmed as no difference can be seen after implementing plans 2 and 4. After 30 years, plans 1 and 2 could suppress the standard exceedance probability the most. Thus, the concentration of toxic leakage should be adopted as the judgment index for repair. When the side impervious wall on both sides is repaired, the leakage risk can be decreased using one of the repair methods.
In each repair strategy, the expected loss value and standard deviation for toxic leakage is calculated using the loss function. In addition, the results of the effect of risk reduction in each repair strategy is compared in Figure 20 according to the risk-expectation model used in financial engineering; the base plan and each repair strategy is plotted on the upper right and bottom left, respectively. The upper-right plot represents a high risk, whereas the bottom-left plot represents a low risk. Plans 1 and 2 are the most effective in reducing loss expectations in each repair strategy. Similarly, repairing both sides of the impervious wall was the most effective in reducing the loss expectations, but not in all repair strategies. This is because the post-repair deterioration curve of the side impervious wall is aligned with the curve of the best-case scenario.
The concentration of toxic substances that leak into the sea area is the most suitable judgment index for repair. The repair strategies can suppress the decrease in water interception performance of the side impervious wall (for which the
![]() (a)
(a)![]() (b)
(b)
Figure 20. Plane indicating risk-expectation of each repair strategy. (a) Repairing the steel side impervious walls on sea-side only; (b) Repairing the steel side impervious walls on the both sides (sea side and landfill site side).
judgment index is the toxic substance concentration in the surrounding water). Moreover, repairing both sides of the side impervious wall can decrease the toxic substance leakage risk.
Because the repair cost and the achieved effect vary according to the difference in the repairing method, the appropriate repair strategy can be determined using a net present value and the LCC. The repair cost is not considered because only the effect of risk reduction is considered in this study. Investment in the maintenance of social infrastructure in Japan is expected to decrease in the future; therefore, the repair strategy must be cost-effective. Cost effectiveness can calculate as follows [4] :
![]() (14)
(14)
The cost-effectiveness of each repair strategy can be defined in terms of the decrease in the leakage risk of the toxic substances. In other words, the monetary value of the reduction in the leakage risk is deducted from that of the leakage risk in the base plan. The repair cost is assumed to be the sum of the material cost of the additional water-swelling material required for repair (Figure 11) and the construction cost. Repairing both sides of the side impervious wall (plan 4) was found to be the most effective, whereas plan 1 is the most cost-effective (Table 7).
The appropriate repair strategy varies according to the decision-making standard adopted in the maintenance strategy. In the maintenance of coastal landfill sites, only the sea-facing side of the side impervious wall need be repaired given the budgetary constraints. However, both sides must be repaired when reducing the leakage risk becomes the top priority. Therefore, an appropriate decision- making standard must be carefully adopted considering the environmental, societal, and financial factors in Japan.
6. Conclusions
The leakage of toxic substances from coastal landfill sites due to deterioration- induced decrease in the water interception performance of side impervious wall was quantitatively evaluated. In addition, asset management-based risk evaluation of the leakage of toxic substances with deterioration of steel side impervious
![]()
Table 7. Effect and cost-effectiveness of each repairing strategy.
walls and selection of an appropriate repair method was discussed. The results of this study can be summarized as follows:
1) Risk assessment considering the uncertainties in future coastal landfill sites was presented. The risk of the retained water leaking to the surroundings due to deterioration of impervious walls was considered the most serious environmental risk of coastal landfills. In the risk assessment, a loss function generally applied in earthquake risk analysis was adopted to determine the standard probability that the index exceeds the limited standard, the loss expectation (and standard deviation) of toxic substance leakage.
2) For social infrastructure, the exceedance probability of 10% after 50 years is considered acceptable; in this study, the risk of leakage was demonstrated to exceed this threshold after 15 years when using steel side double impervious walls. However, whether steel side double impervious walls can adequately contain toxic substances over time and with deterioration remain unclear.
3) An appropriate risk assessment-based maintenance strategy was proposed. The repair of the side impervious wall was used as the countermeasure, and the repair time and location that resulted in the largest reduction in the leakage risk were identified. The strategy of repairing when the concentration of the toxic substances leaking into the sea area exceeds that caused by the closure or abandonment of coastal landfill sites was shown to be the most effective. Moreover, the strategy of repairing only the sea-facing side impervious wall was found to be the most cost-effective.
Acknowledgements
This research was a part of the project titled “Development on technology for offshore waste final disposal”, funded by the Ministry of Oceans and Fisheries, Korea.