New Blind Recognition Method of SCLD and OFDM in Alpha-Stable Noise ()
1. Introduction
With wide application of OFDM, the recognition of OFDM signal has become a hot issue in various fields of applications among cognitive radio and military applications. Algorithms for the recognition of OFDM versus SCLD signals in AWGN scenario have been reported in [1]-[6]. The algorithm proposed in [1] is based on the signal empirical distribution function to recognize OFDM. Fourth- and sixth-order signal moments are employed in [2] to identify OFDM and single-carrier. Wavelet analysis is also employed to distinguish OFDM and SCLD in [3] [4]. The algorithm proposed is based on the second-order cyclic cumulate to recognize OFDM versus SCLD signals under time dispersive channel in [5]. Based on the spectrum analysis, an algorithm was proposed to recognize OFDM in [6]. The above results were developed under the simplified assumption of additive white Gaussian noise channel. But, many noise processes are impulsive in nature. Impulsive channels have been arisen in underwater (ice-cracks), atmospheric (thunderstorms) environments, and other mobile communication problems [7]. Impulsive noise can be modelled as alpha-stable distribution process which is different from Gaussian noise. When the communication channel in nature is impulsive channel modelled as alpha-stable distribution process, the existing recognition algorithms of OFDM versus SCLD would become invalid, because the impulsive noise does not have second-order and higher order statistics. For this reason, we study the recognition of OFDM against SCLD signals in alpha-stable noise here. In this paper, we extract new modulation classification features from the new results concerning the generalized cyclostationarity of OFDM and SCLD signals in alpha-stable noise, and use support vector machine (SVM) as classifier to these signals. The recognition algorithm avoids the need for timing and carrier recovery and the estimation of signal and noise powers. Simulation results show that the proposed method have good performances in alpha-stable noise.
The rest of the paper is organized as follows. The SCLD and OFDM signal models is presented in Sections 2, the proposed recognition algorithm is introduced in Section 3 and simulation results are discussed in Section 4. Finally, our conclusions are presented in Section 5.
2. Signal Models
The received signal can be written as,
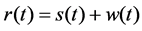 (1)
(1)
where  means the transmitted signal,
means the transmitted signal, 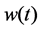 is alpha-stable noise.
is alpha-stable noise.
If the modulation type of the transmitted signal is OFDM, 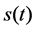 can be represented by
can be represented by , which is expressed as,
, which is expressed as,
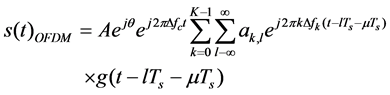 (2)
(2)
where 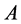 is the amplitude,
is the amplitude, 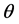 is the phase,
is the phase,  is the carrier frequency offset,
is the carrier frequency offset, 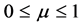 is the timing offset,
is the timing offset, 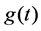 is the overall impulse response of the transmit and receive filters,
is the overall impulse response of the transmit and receive filters,  is the number of subcarriers of the OFDM signal,
is the number of subcarriers of the OFDM signal,  is the symbol transmitted on the kth subcarrier over the lth symbol period,
is the symbol transmitted on the kth subcarrier over the lth symbol period, 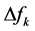 is the frequency separation between two adjacent subcarriers,
is the frequency separation between two adjacent subcarriers, 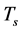 is the OFDM symbol period, and
is the OFDM symbol period, and . The data symbols
. The data symbols 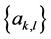 are assumed to be zero-mean independent and identically distributed (i.i.d.) random variables, with values drawn either from a quadrature amplitude modulation (QAM) or phase shift keying (PSK) constellation.
are assumed to be zero-mean independent and identically distributed (i.i.d.) random variables, with values drawn either from a quadrature amplitude modulation (QAM) or phase shift keying (PSK) constellation.
If the modulation type of the transmitted signal is SCLD,  can be represented by
can be represented by![]() , which is expressed as,
, which is expressed as,
![]() (3)
(3)
where ![]() is the amplitude,
is the amplitude, ![]() is the carrier phase,
is the carrier phase, ![]() is the frequency offset,
is the frequency offset, ![]() is the symbol period,
is the symbol period, ![]() is the timing offset,
is the timing offset, ![]() is the overall impulse response of the transmit and receive filters,
is the overall impulse response of the transmit and receive filters, ![]() is the symbol transmitted in the lth symbol period. The data symbols
is the symbol transmitted in the lth symbol period. The data symbols ![]() are assumed to be zero-mean independent and i.i.d., with values drawn either from a quadrature amplitude modulation (QAM) or phase shift keying (PSK) constellation.
are assumed to be zero-mean independent and i.i.d., with values drawn either from a quadrature amplitude modulation (QAM) or phase shift keying (PSK) constellation.
The alpha-stable noise ![]() is defined by its characteristic function, since a closed form expression for its probability density function (pdf) is not always available. The characteristic function
is defined by its characteristic function, since a closed form expression for its probability density function (pdf) is not always available. The characteristic function ![]() is given by [8],
is given by [8],
![]() (4)
(4)
In (4), ![]() and
and ![]() is given as,
is given as,
![]() (5)
(5)
and
![]() (6)
(6)
where ![]() ,
, ![]() , and
, and ![]() are the characteristic exponent, dispersion, and location, respectively. Without loss of generality, noise employs standard symmetric alpha-stable distribution-SαS as model. Because the SαS noise do not have finite second moment, its noise variance loses meaning. So a mixed signal to noise ratio-MSNR is employed, MSNR is given by [8],
are the characteristic exponent, dispersion, and location, respectively. Without loss of generality, noise employs standard symmetric alpha-stable distribution-SαS as model. Because the SαS noise do not have finite second moment, its noise variance loses meaning. So a mixed signal to noise ratio-MSNR is employed, MSNR is given by [8],
![]() (7)
(7)
where ![]() represents the signal variance and
represents the signal variance and ![]() is dispersion of alpha-stable noise.
is dispersion of alpha-stable noise.
3. The Recognition Algorithm of OFDM and SCLD in Alpha-Stable Distributed Noise
3.1. The Generalized Second-Order Cyclic Statistics of OFDM and SCLD
Alpha-stable noise does not have second-order and higher order statistics so that many traditional OFDM identification algorithms will be invalid. To solve the problem that traditional second-order cyclic statistics significantly degenerate in the alpha-stable noise, the concept of generalized second-order cyclic statistics was proposed in [9]. The core of the concept is by use of some kind of nonlinear transformation to suppress the pulse noise, and then process the transformed signal by traditional second-order cyclic statistical analysis. Taking advantages of the concept, a new method to recognize modulation type between OFDM and SCLD in this paper. Firstly, a nonlinear transformation function is defined as following to transform the received signal
![]() (8)
(8)
where ![]() represents the received signal.
represents the received signal.
The autocorrelation function of signal ![]() can be expressed as,
can be expressed as,
![]() (9)
(9)
When MSNR is higher enough, ![]() , (9) can be approximated as,
, (9) can be approximated as,
![]() (10)
(10)
where![]() ,
,
![]() ,
, ![]() represents autocorrelation information
represents autocorrelation information
of![]() . When
. When![]() , the amplitude of noise is suppressed. Obviously, when processing the received signal
, the amplitude of noise is suppressed. Obviously, when processing the received signal ![]() with nonlinear transformation, the unique features of signal
with nonlinear transformation, the unique features of signal ![]() are maintained in
are maintained in![]() , and the amplitude of noise is effectively limited. For the OFDM signal, (2) can be put into (10) and (10) becomes
, and the amplitude of noise is effectively limited. For the OFDM signal, (2) can be put into (10) and (10) becomes
![]() (11)
(11)
where ![]() is the information data transmitted within the kth subcarrier, and the data is assumed to be i.i.d.. Hence, (11) can be further re-written as,
is the information data transmitted within the kth subcarrier, and the data is assumed to be i.i.d.. Hence, (11) can be further re-written as,
![]() (12)
(12)
where![]() ,
,
![]() ,
, ![]() represents the complex conjugate,
represents the complex conjugate, ![]() stand
stand
for operator, which maintain the phase of signal, ![]() is the Dirac delta function and
is the Dirac delta function and ![]() is convolution. From (12) one can see that
is convolution. From (12) one can see that ![]() is a periodic function with fundamental periodic
is a periodic function with fundamental periodic![]() . The autocorrelation function can be easily expressed as a Fourier series, and the Fourier transform of (12) yields
. The autocorrelation function can be easily expressed as a Fourier series, and the Fourier transform of (12) yields
![]() (13)
(13)
where ![]() denotes the Fourier transform. Furthermore, by expressing the convolution, using a change of variables and the identity
denotes the Fourier transform. Furthermore, by expressing the convolution, using a change of variables and the identity
![]() , one can show that (13) becomes
, one can show that (13) becomes
![]() (14)
(14)
where![]() . Note that (14) give the
. Note that (14) give the
analytical expressions for the generalized second-order cyclic statistics at ![]() and certain delay. According to (14), when
and certain delay. According to (14), when![]() ,
, ![]() yields significant peaks. Meanwhile, the magnitude peaks of
yields significant peaks. Meanwhile, the magnitude peaks of ![]() are visible at
are visible at![]() and
and![]() , with
, with ![]() as an integer.
as an integer.
As one can notice, when processing the received signal ![]() with nonlinear transformation, the modulated information of received signal
with nonlinear transformation, the modulated information of received signal ![]() is maintained in the
is maintained in the![]() . For the OFDM signal, significant peaks occur in the vicinity of
. For the OFDM signal, significant peaks occur in the vicinity of ![]() and
and![]() .
. ![]() stands for noise interference, and its impact has been suppressed due to the nonlinear transformation.
stands for noise interference, and its impact has been suppressed due to the nonlinear transformation.
Similarly, for the SCLD signal, we obtain
![]() (15)
(15)
where ![]() is information data transmitted and the data is assumed to be i.i.d.. According to (15), the magnitude peaks of
is information data transmitted and the data is assumed to be i.i.d.. According to (15), the magnitude peaks of ![]() are visible at
are visible at ![]() and
and![]() .
.
3.2. The Generalized Cyclostationarity-Based Recognition Method of OFDM and SCLD Signals
Based on the above results on signal the generalized cyclic statistics, here we develop a novel algorithm for the recognition of OFDM and SCLD signals in alpha-stable noise.
Under the assumption of no aliasing, for the discrete-time signal
![]() , obtained by sampling the continuous-time signals
, obtained by sampling the continuous-time signals ![]() at the
at the
sampling rate![]() . According to the discussed in Section 3.1, we obtain
. According to the discussed in Section 3.1, we obtain
![]() (16)
(16)
Then, for the OFDM signal, ![]() can be written as
can be written as
![]() (17)
(17)
where![]() ,
,
![]() ,
, ![]() denotes OFDM symbol length, and
denotes OFDM symbol length, and![]() ,
, ![]() is the useful symbol length and
is the useful symbol length and ![]() is the cyclic
is the cyclic
prefix length. From (17) one can see that ![]() is a periodic function, with fundamental periodic
is a periodic function, with fundamental periodic![]() . Thus
. Thus ![]() can be expressed as a Fourier series, and the Fourier transform of (17) yields
can be expressed as a Fourier series, and the Fourier transform of (17) yields
![]() (18)
(18)
where![]() , the significant peaks of
, the significant peaks of ![]() can be obtained at
can be obtained at![]() . Furthermore, from (18) it can be noticed that magnitude peaks are visible at
. Furthermore, from (18) it can be noticed that magnitude peaks are visible at ![]() and
and![]() , with
, with ![]() as an integer.
as an integer.
Similarly, for the SCLD signal, we obtain
![]() (19)
(19)
where![]() ,
, ![]() is information of data transmitted
is information of data transmitted
and the data is assumed to be independent and identically distributed. ![]() denotes symbol length of SCLD. According to (19), magnitude peaks of are visible at
denotes symbol length of SCLD. According to (19), magnitude peaks of are visible at ![]() and
and![]() , with
, with ![]() as an integer.
as an integer.
When comparing (18) and (19), one can easily notice the additional factor ![]() which appears in the expression of the generalized cyclic statistics of the OFDM signal. One can easily show that significant peaks of the generalized cyclic statistics of OFDM signal yields at
which appears in the expression of the generalized cyclic statistics of the OFDM signal. One can easily show that significant peaks of the generalized cyclic statistics of OFDM signal yields at ![]() and
and![]() . The existence of such a peak in the magnitude of the generalized cyclic statistics of the OFDM signal (at
. The existence of such a peak in the magnitude of the generalized cyclic statistics of the OFDM signal (at ![]() and
and![]() ) is employed as discriminating feature to identify OFDM against SCLD signals.
) is employed as discriminating feature to identify OFDM against SCLD signals.
The estimate of the generalized cyclic statistics ![]() exist the estimation error factor which vanishes asymptotically is
exist the estimation error factor which vanishes asymptotically is![]() . Due to the existence of estimation error factor, the estimator seldom exactly zero in practice, even if
. Due to the existence of estimation error factor, the estimator seldom exactly zero in practice, even if ![]() is not at generalized cycle frequencies. In order to decrease the impact of estimation error factor, referencing [10], the modulation classification features are given as,
is not at generalized cycle frequencies. In order to decrease the impact of estimation error factor, referencing [10], the modulation classification features are given as,
![]() (20)
(20)
where![]() ,
, ![]() is tested candidate frequency and
is tested candidate frequency and ![]() represents tested candidate delay,
represents tested candidate delay, ![]() is the received signal length. Here
is the received signal length. Here ![]() and
and ![]() denote transpose and matrix inverse,
denote transpose and matrix inverse, ![]() is an estimate of the covariance matrix
is an estimate of the covariance matrix
![]() (21)
(21)
with covariance estimators are respectively given by,
![]() (22)
(22)
and
![]() (23)
(23)
where![]() ,
, ![]() is a spectral window of support
is a spectral window of support ![]() (odd).
(odd).
According to the above analysis, the steps of recognizing OFDM against SCLD modulations may be obtained as follows:
Step 1: The magnitude of the generalized second-order cyclic statistics ![]() of the received signal is estimated. Firstly, the discrete-time signal
of the received signal is estimated. Firstly, the discrete-time signal ![]() obtained by sampling the continuous-time signal
obtained by sampling the continuous-time signal ![]() at the sampling rate
at the sampling rate![]() . Then, the nonlinear transformation function in (8) is used to map received signal
. Then, the nonlinear transformation function in (8) is used to map received signal![]() . Finally, the normalization magnitude of the second-order cyclic statistics
. Finally, the normalization magnitude of the second-order cyclic statistics ![]() of the transformed signal
of the transformed signal ![]() is estimated.
is estimated.
Step 2: The modulation classification features ![]() is extracted from
is extracted from![]() . Search the maximum
. Search the maximum ![]() value at
value at ![]() section, and the delays
section, and the delays ![]() in the interval
in the interval ![]() (with and as the minimum and maximum number of subcarriers that we consider). Then, the modulation classification features
(with and as the minimum and maximum number of subcarriers that we consider). Then, the modulation classification features ![]() is extracted with (20).
is extracted with (20).
Step 3: The modulation type is decided. Classify the test signal by employing the SVM classifier defined in the training procedure.
4. Simulation Results and Analysis
A. Simulation setup
For the SCLD signals, we consider a pool of QPSK and 16-QAM. With the OFDM signals, the subcarriers are modulated using QPSK or 16-QAM. Unless otherwise mentioned, for the OFDM signal, the number of subcarriers is set to 64, the useful time period of the OFDM symbol is set to 0.0128 s and the cyclic prefix period is set to 0.0032s. In addition, frequency offset is set to 1 kHz and 2 kHz for SCLD and OFDM signals, and ![]() to 0.75, as
to 0.75, as ![]() a random variable uniformly distributed over
a random variable uniformly distributed over![]() . The SVM classifier is implemented by utilizing the LIBSVM toolbox, where the Gaussian RBF is selected as the kernel function. Let
. The SVM classifier is implemented by utilizing the LIBSVM toolbox, where the Gaussian RBF is selected as the kernel function. Let ![]() be the training sequence composed of
be the training sequence composed of ![]() at the different MSNR, where
at the different MSNR, where![]() , with V as the number of the training sequences. The number of training and test sequences is respectively set to 100 for each class at each MSNR.
, with V as the number of the training sequences. The number of training and test sequences is respectively set to 100 for each class at each MSNR.
B. Generalized second-order cyclic statistics magnitude estimates for the OFDM and SCLD signals
The estimated magnitude of the generalized cyclic statistics of OFDM and SCLD is plotted. For SαS noise, MSNR = 10 dB and![]() .
.
When comparing results presented in Figure 1 and Figure 2, one can notice that the second-order cyclic spectrum of OFDM signal is destroyed by alpha-stable noise, but the generalized second-order cyclic statistics of OFDM signal yields significant peaks at ![]() and
and![]() . Figure 3 shows that the generalized second-order cyclic statistics of SCLD signal can keep the characteristics of second-order cyclic statistics. However, Figure 4 shows that the second-order cyclic statistics of SCLD signal is destroyed by alpha-stable noise. From Figure 1 and Figure 3 one can notice that the existence of such a peak in
. Figure 3 shows that the generalized second-order cyclic statistics of SCLD signal can keep the characteristics of second-order cyclic statistics. However, Figure 4 shows that the second-order cyclic statistics of SCLD signal is destroyed by alpha-stable noise. From Figure 1 and Figure 3 one can notice that the existence of such a peak in
![]()
Figure 1. Generalized second-order cyclic statistics of OFDM signal.
![]()
Figure 2. Second-order cyclic statistics of OFDM signal.
![]()
Figure 3. Generalized second-order cyclic statistics of SCLD signal.
![]()
Figure 4. Second-order cyclic statistics of SCLD signal.
the magnitude of the generalized cyclic statistics of the OFDM signal (at ![]() and
and![]() ) is employed as discriminating feature to recognize OFDM against SCLD signals.
) is employed as discriminating feature to recognize OFDM against SCLD signals.
C. Performance of proposed recognition algorithm
Without loss of generality, set![]() . 200 tests for each MSNR value, and observation interval is set to 0.32 s. The simulation results are shown in Figure 5.
. 200 tests for each MSNR value, and observation interval is set to 0.32 s. The simulation results are shown in Figure 5.
In Figure 5, the probability of correctly recognizing an OFDM signal is plotted versus MSNR. According to Figure 5, the algorithm based on traditional second-order cyclic statistics severely degraded within the range of the entire MSNR, but the proposed algorithm has a significant performance advantage. Note that the probability of correct detection and OFDM signal of the proposed
![]()
Figure 5. The probability of correct recognition in standard SαS noise.
![]()
Figure 6. The probability of correct recognition with different values of a.
method is almost 100% at 0 dB. This simulation results for the algorithm performance confirm its effectiveness in alpha- stable distribution noise.
D. Effect of the a value on algorithm performance
In this experiment, set MSNR = 0 dB, a changes with the step 0.1 in the interval [0.1, 1.9]. The observation interval is set to 0.32 s, and 200 tests for each a value. The simulation results are shown in Figure 6.
Figure 6 shows performance results obtained for different values of a with the proposed algorithm. From Figure 6 as can be seen simultaneously, the smaller the a value, the greater error of correct recognition. The reason is that the smaller![]() value and the more obvious peak characteristics of alpha-stable distribution. The probability of correct recognition of OFDM is 100%, when
value and the more obvious peak characteristics of alpha-stable distribution. The probability of correct recognition of OFDM is 100%, when![]() . This simulation result that the proposed method is suitable for different values of a in the interval [1, 2).
. This simulation result that the proposed method is suitable for different values of a in the interval [1, 2).
5. Conclusion
This paper proposes a novel modulation identification algorithm for OFDM and SCLD in alpha-stable distributed noise. The generalized second-order cyclic statistics can be exploited for the recognition of OFDM against SCLD signals. The proposed recognition algorithm eliminates the need for preprocessing tasks, such as symbol timing estimation, carrier and waveform recovery, and signal and noise power estimation. Simulation results show that the algorithm have good estimation performance and high robustness.